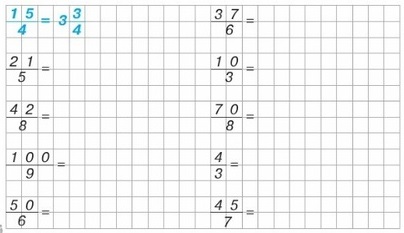
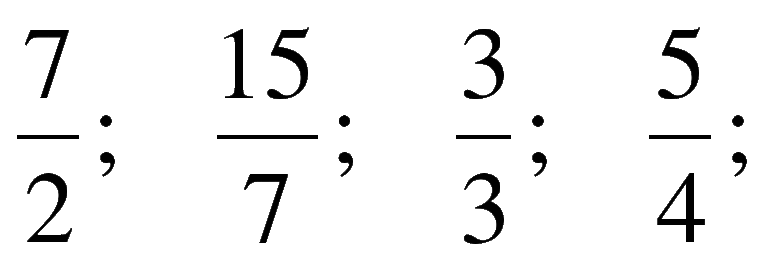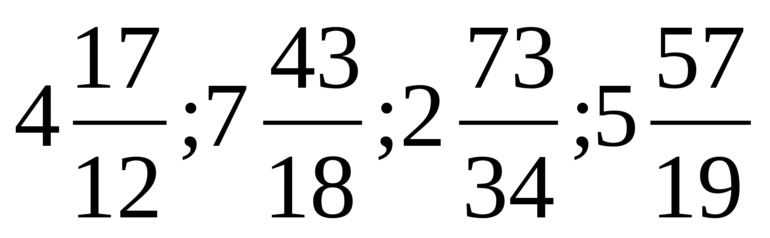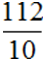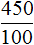найди неправильную дробь которую можно превратить в целое число
Как неправильную дробь превратить в смешанное число?
Любую неправильную дробь можно превратить в смешанное число. Для этого числитель дроби разделим на знаменатель. Получится целое число и остаток. Число — это целая часть дроби. Остаток – это числитель дроби. А знаменатель остается тем же, т.е число на которое мы делили.
Давайте разбираться.
1.
3. Давайте потренируемся:
Проверка: 15 / 4 — это 15 : 4. 15 на 4 не делится нацело: делим 12 на 4 = 3, значит, 3 целых. Находим дробь: 15 – 12 = 3, т.е. осталось 3 – это числитель, т.е. три четвертых, потому что мы делим на 4.
21/5 — это 21 : 5. 21 на 4 не делится нацело: делим 20 на 5 = 4, значит, 4 целых. Находим дробь: 21 – 20 = 1, т.е. осталось 1 – это числитель дроби, т.е. одна пятая, потому что мы делим на 5.
42/8 – это 42 : 8. 42 на 8 не делится нацело: делим 40 на 8 = 5, значит, 5 целых. Находим дробную часть: 42 – 40 = 2, т.е. осталось 2 – это числитель дроби, т.е. две восьмых, потому что мы делим на 8.
100/9 – это 400 : 9. 100 на 9 не делится нацело: делим 99 на 9 = 11, значит, 11 целых. Находим дробную часть: 100 – 99 = 1, т.е. осталось 1 – это числитель дроби, т.е. одна девятая, потому что мы делим на 9.
50/6 – это 50 : 6. 50 на 6 не делится нацело: делим 48 на 6 = 8, значит, 8 целых. Находим дробную часть: 50 – 48 = 2, т.е. осталось 2 – это числитель дроби, т.е. две шестых, потому что мы делим на 6.
37/6 – это 37 : 6. 37 на 6 не делится нацело: делим 36 на 6 = 6, значит, 6 целых. Находим дробную часть: 37 – 36 = 1, т.е. осталось 1 – это числитель дроби, т.е. одна шестая, потому что мы делим на 6.
10/3 – это 10 : 3. 10 на 3 не делится нацело: делим 9 на 3 = 3, значит, 3 целых. Находим дробную часть: 10 – 9 = 1, т.е. осталось 1 – это числитель дроби, т.е. одна третья, потому что мы делим на 3.
70/8 – это 70 : 8. 70 на 8 не делится нацело: делим 64 на 8 = 8, значит, 8 целых. Находим дробную часть: 70 – 64 = 6, т.е. осталось 6 – это числитель дроби, т.е. шесть восьмых, потому что мы делим на 8.
4/3 – это 4 : 3. 4 на 4 не делится нацело: делим 3 на 3 = 1, значит, 1 целая. Находим дробную часть: 4 – 3 = 1, т.е. осталось 1 – это числитель, т.е. она третья, потому что мы делим на 3.
45/7 – это 45 : 7. 45 на 7 не делится нацело: делим 42 на 7 = 6, значит, 6 целых. Находим дробную часть: 45 – 42 = 3, т.е. осталось 3 – это числитель, т.е. три седьмых, потому что мы делим на 7.
Неправильная дробь
Что такое неправильная дробь
Неправильной называется дробь, числитель которой по своей величине превышает знаменатель либо одинаков с ним.
Основные математические действия с неправильными дробями
Неправильная дробь — полноценный представитель числового множества, поэтому с ней можно производить основные математические действия:
Сравнение
6 / 5 7 / 5 ; 9 / 7 > 8 / 7 ; 5 / 5 = 5 / 5
Однако, бывает необходимо вычислить, насколько значение неправильной дроби больше (либо меньше) значения другой неправильной дроби с иным знаменателем.
Сложение
Определить сумму двух неправильных дробей с одинаковым знаменателем легко: 5/4+7/4=12/4=3
Схематически это можно записать с помощью формулы:
Сложение неправильных дробей с различными знаменателями. Для таких случаев существует два варианта: перевести дроби в смешанные либо использовать правило для перехода к общему знаменателю.
Переход к смешанным дробям осуществляется путем деления числителя на знаменатель (бывает, что с остатком):
Тактика приведения к общему знаменателю при сложении неправильных дробей (и их вычитании) следующая:
Аналогичным образом поступают, когда необходимо провести вычитание с неправильными дробями.
Умножение
При умножении друг на друга двух неправильных дробей получается дробь, числитель которой равен произведению числителей первоначальных дробей, а знаменатель — произведению знаменателей.
Деление
При делении неправильных дробей деление имеет обратное свойство. Делитель необходимо записать наоборот: числитель и знаменатель поменять местами. Когда это проведено, делимое умножают на делитель и получают искомый результат.
Перевод неправильной дроби в смешанную дробь и обратно
Неправильную дробь можно легко перевести в смешанную, произведя следующие действия:
Например, необходимо превратить в смешанную дробь 13/8.
Разделив 13 на 8, получаем 1 и 5/8. Разделив 5 на 8, получаем 0,625. В итоге 1,625.
Бывают случаи, когда нужно произвести обратное действие: превратить смешанную дробь в неправильную. Объяснение изложено в следующей формуле:
Подставим в эту формулу значения. 21 / 3 = ( 1 + 2 * 3 ) / 3 = 7 / 3
Примеры задач
Рассмотрим приведенные выше правила на примерах.
Сложение с одинаковым знаменателем: 8 / 5 + 7 / 5 = 15 / 5 = 3
Объяснение: приводим слагаемые к общему знаменателю. Для этого на знаменатель правой дроби умножаем числитель левой, а знаменатель левой — на числитель правой. В знаменателе дроби-произведения стоит произведение обоих знаменателей. После проведения расчетов получается смешанная дробь 3,625.
Объяснение: приводим вычитаемые к общему знаменателю. Для этого на знаменатель правой дроби умножаем числитель левой, а знаменатель левой — на числитель правой. В знаменателе дроби-частного стоит произведение обоих знаменателей. После проведения расчетов получается смешанная дробь 3,875.
Задача на умножение:
7 / 5 * 9 / 4 = 63 / 20
8 / 6 * 10 / 9 = 80 / 54
Объяснение: умножаем числитель на знаменатель и получаем искомое произведение.
4 / 7 : 2 / 5 = 4 / 7 * 5 / 2 = ( 4 * 5 ) / ( 7 * 2 ) = 20 / 14 = 16 / 14
Поменяв местами числитель и знаменатель в делителе, производим действие умножения двух дробей. После этого в числителе итоговой дроби ставится произведение двух числителей, а в ее знаменателе — произведение двух знаменателей.
Общие сведения
Знакомить с дробями начинают в начальной школе. Чтобы ребёнок смог непросто заучить, а понять, что обозначает этот термин, применяют наглядный пример. В качестве его лучше использовать какое-либо круглое тело.
Пусть есть торт. Он один, поэтому представляет собой некое целое. Его можно разрезать на несколько равных частей. Например, 8. Получается, что из чего-то общего возможно выделить части. Количественно каждый кусок будет занимать 1/8 от пирога. Аналогично можно рассмотреть отрезок длиной 10 см. Каждый его 1 см будет составлять от целой длины 1/10.
Из 8 отрезанных кусочков 3 съели. На блюде осталось 5 одинаковых частей. По-другому их называют долями. Это изменение количества в математике произносят, как пять восьмых, то есть из целого после какого-то действия осталась определённая часть.
Записывать такое отношение принято в виде двух чисел, разделённых чертой. Называется она дробной и обозначает деление. Для примера с тортом выражение будет выглядеть как 1/8 и 5/8. Верхняя часть называется числитель и обозначает делимое, а нижняя — знаменатель, то есть делитель. Другими словами, первое число показывает, сколько частей взято, а нижнее, на какое число долей было разделено целое.
Такая дробь считается обыкновенной. Она может быть двух видов:
Кроме обыкновенной дроби, выделяют ещё 2 типа выражений — десятичные и смешанные. Если первое есть не что иное, как запись рациональной дроби со знаменателем кратным десяти, то второе — число, состоящее из целой части и правильного выражения. Например, 3 8/9.
Понимается эта запись как сумма целого числа и дробного. То есть 3 + 8/9. Если выполнить операцию сложения, в ответе получится дробь, у которой числитель больше знаменателя. Любое смешанное выражение можно преобразовать в неправильное. Это утверждение справедливо и для обратного превращения. Например, запись 47/8 будет тождественной выражению 5 7/8.
Необходимость преобразования
С дробными числами можно выполнять различного вида математические действия: складывать, вычитать, перемножать и делить, возводить в степень и логарифмировать. Но при этом существует негласное правило, согласно которому все операции нужно выполнять только после приведения выражений к одному типу. Конечно, сложить или разделить смешанную дробь на неправильную возможно, но алгоритм действий будет нерациональным, что приведёт к появлению ошибок при вычислении.
Преобразовывать можно любую дробь. Из десятичной легко сделать правильную: 0,5 = 5/10. Из смешанной неправильную — 1 2/5 = 7 / 5. Эти операции выполняются и в обратную сторону. Единственным исключением является задача сделать из неправильной дроби правильную.
Запись, у которой делимое меньше делителя, нельзя представить как число с числителем меньше знаменателя. Но здесь на помощь и приходит смешанное выражение, то есть чтобы из неправильной дроби сделать правильную, нужно из первого числа выделить целую часть. В итоге получится выражение, состоящее из суммы двух чисел: неделимого и правильного.
Следует отметить ещё один важный момент. Перед тем как переводить дробь в неправильную или любую другую, нужно попробовать выполнить ряд упрощений. Это позволит в дальнейшем сложные вычисления заменить простыми. Выполнять упрощение возможно, основываясь на свойствах дробей:
Эти правила называют основным свойством дробного числа или операцией сокращения. Например, 18/6 = 3/1 = 3. Числитель и знаменатель был разделён на 3. Тот же результат будет получен, если делитель и делимое помножить на любое число: 18/6 = 18*2 /6*2 = 36 / 12 = 3. Действительно, правильность утверждения можно доказать простым анализом.
Пусть есть равенство: a/b = z. Нужно доказать, что a*n/b*n = z. Так как черта обозначает деление, используя связь между ним и умножением, исходное выражение можно переписать: a = b*n. Согласно свойствам числовых неравенств, обе части разрешается умножить на число, отличное от нуля. Тогда a*n = (b*z)*n. В соответствии с переместительным законом n и z можно поменять местами: a*n = (b*n)*z. Отсюда: z = a*n/(b*n). Что и нужно было доказать.
Алгоритм превращения
Переводить неправильную дробь в правильную или выполнять обратную операцию просто, если следовать алгоритму. Так как сделать это напрямую нельзя, то фактически получится преобразование в запись, содержащую целую и дробную часть.
Превратить неправильное выражение в смешанное можно по следующему алгоритму:
Это упрощённый способ, быстро позволяющий выполнить перевод числа из одной формы в другую. Математическое равенство, описывающее это правило, будет выглядеть так: n a/b = ((n * b) + a)/b.
Чтобы преобразовать дробь по всем правилам, нужно сделать следующее. Так как смешанное отношение, по сути, является суммой целого и части, понадобится просто выполнить сложение. Для этого первое слагаемое представляют как неправильную дробь. Сделать это можно, разделив целое на единицу. Затем действуют по правилу сложения дробей, то есть находят общий знаменатель, дополнительные множители, выполняют складывание в числителе: n a/b = n/1 + a/b = ((n *b) + a)/b.
Из неправильной формы записи получить обычную дробь можно также через смешанную. Другими словами, представить выражение как сумму натурального числа и правильного отношения. Для этого необходимо выполнить 3 шага:
На самом деле выполнять деление числителя на знаменатель часто довольно сложно, поэтому поступают следующим образом. Делимое представляют в виде суммы дробей, но таким образом, чтобы деление одной из них можно было выполнить без остатка, то есть, m / n = (k + c) / n = k / n + c / n. Где целое число k / n, а c / n правильная дробь.
Нужно отметить, что некоторые выражения можно превращать в другую форму, не записывая поочерёдно действия, а выполняя все преобразования в уме. Но на начальном этапе рекомендуется весь процесс расписывать пошагово, пока не будет получен необходимый опыт. А только уже после переходить к переводу в уме.
Примеры решения
Несмотря на то что операция по превращению довольно простая, для её успешного применения необходим опыт, поэтому следует потренироваться не только в простом преобразовании, но и увидеть полезность действий на практике. Вот некоторые примеры, рассчитанные на учащихся четвёртых классов, рекомендуемые к самостоятельному решению:
В интернете существуют сервисы, позволяющие в автоматическом режиме выполнять перевод из одной формы записи в другую. Чтобы воспользоваться услугами таких онлайн-калькуляторов, необязательно знать принцип преобразования. Доступ к услугам не требует регистрации или введения каких-либо персональных данных. Нужно просто иметь гаджет с подключённым интернетом и любой веб-браузер. Всё, что требуется от пользователя — ввести в предлагаемую форму исходную дробь и нажать кнопку «Рассчитать». Через несколько секунд на экран будет выведен ответ.
Кроме расчёта результата, многие такие математические сервисы дают возможность ознакомиться с подробным решением. Это хорошая возможность для учащихся закрепить полученные знания. Ведь можно не только проверить самостоятельное решение, но и понять, как получается тот или иной ответ. Причём на страницах сайтов содержится в кратком виде и теоретический материал с подробным описанием решения примеров.
Как превратить неправильную дробь в десятичную
В неправильной дроби – числитель всегда больше знаменателя.
Рассмотрим на примерах.
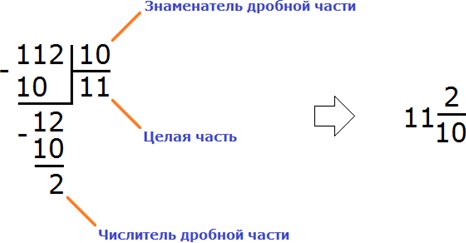
Выделяем целое.
Дробная черта заменяет знак деления.
Выполняем деление, удобнее — «уголком»:
Мы видим, что значение частного – это целое, остаток – это числитель, а делитель – знаменатель.
Теперь полученное смешанное число превращаем в десятичную дробь (см. здесь).
Получим – 11,2 – «одиннадцать целых две десятых».
Ответ: 11,2.
Выделяем целое – делим «уголком».
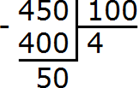
Переводим его в десятичную дробь.
4,50
Мы знаем, что нули в конце десятичной части можно убрать. От этого дробь не изменится. Таким образом — 4,50 = 4,5.
Ответ: 4,5.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 62