какое высказывание является истинным

Какое высказывание является истинным

Тема 3. Основы математической логики 1. Логические выражения и логические операции.
2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

1. Логические выражения и логические операции

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).

Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.

Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.

Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.

С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.

Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.

В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.

Существуют разные варианты обозначения истинности и ложности логических переменных:

Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Введем перечисленные логические операции.

В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Источник

Истинные и ложные высказывания. Составные высказывания.

Форма: урок изучения нового материала.

Цель: познакомить обучающихся с истинными и ложными высказываниями, познакомить с правилом определения истинности высказывания.

Задачи:

Образовательные: учить отличать истинные высказывания от ложных,

Развивающие: развивать логическое мышление, память, наблюдательность, математическую речь.

Воспитательные: воспитывать рассудительность, трудолюбие, внимательное отношение к мнению других,умение работать в коллективе.

Универсальные учебные действия:

Познавательные: принимать и сохранять учебную задачу, использовать знаково-символические средства, для решения задач.

Регулятивные: планировать своё действие в соответствии с поставленной задачей.

Коммуникативные: развернуто обосновывать суждения, давать определения, приводить доказательства.

Личностные: уважительное отношение к мнению других, внутренняя позиция школьника на основе положительного отношения к школе.

Оборудование: УМК «Начальная школа 21 века», технологическая карта урока, учебник, презентация, тетрадь, карточки с заданиями для групповой работы.

Ход урока.

Этапы урока

Деятельность учителя

Деятельность ученика

Планируемые результаты.

I.Организация класса.

— Здравствуйте, ребята! Давайте настроимся на сегодняшний урок. Повернитесь к своему соседу по парте и улыбнитесь ему. Пожелайте ему хорошего настроения и успехов на уроке. Наш урок мы начнём с устного счёта.

Проверяют свою готовность к уроку, учатся налаживать эмоциональный контакт друг с другом и с учителем.

Коммуникативные: взаимодействие с учителем и одноклассниками, уметь слушать, понимать речь других, соблюдать простейшие нормы школьного этикета.

Личностные: самоопределение к деятельности, настрой на урок.

Регулятивные: организовывать свою деятельность.

II.Актуализация знаний.

«Устный счёт».

а) – Выполните действия.

6000 + 3000 + 200+ 5= 9205

(14350 − 350) : 100 = 14000 : 100= 140

18000 + 5000 + 300 = 23300

Девизом нашего урока будут следующие слова «Считай несчастным тот день и тот час, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию». Запомните этот девиз.

Формулируют ответы на вопросы, оценивают свою работу.

Коммуникативные: слушать и понимать речь других; использовать речевые средства для аргументации своей позиции.

Личностные: учиться уважительно относится к одноклассникам, применять правило делового сотрудничества.

Регулятивные: оценивать сложившуюся учебную ситуацию; высказывать свои предположения.

Познавательные: находить ответы на вопросы, используя свой жизненный опыт; использовать полученные знания на практике.

III. Изучение нового материала.

Источник

Какое высказывание является истинным

Простые и сложные высказывания, логиче­ские переменные и логические константы, логическое отрицание, логическое умноже­ние, логическое сложение, таблицы истин­ности для логических операций

Для описания рассуждений и правил выполне­ния действий с информацией используют специаль­ный язык, принятый в математической логике. В осно­ве рассуждений содержатся специальные предложе­ния, называемые высказываниями. В высказываниях всегда что-либо утверждается или отрицается об объ­ектах, их свойствах и отношениях между объекта­ми. Высказыванием является любое суждение, отно­сительно которого можно сказать, истинно оно или ложно. Высказываниями могут быть только повест­вовательные предложения. Вопросительные или по­будительные предложения высказываниями не явля­ются.

Высказывание — суждение, сформулированное в виде по­вествовательного предложения, о котором можно сказать, истинно оно или ложно.

Например, вопросительные предложения «В каком году было первое летописное упоминание о Москве?» и «Что является внешней памятью компьютера?» или побудительное предло­жение «Соблюдайте правила техники безопасности в компью­терном классе» высказываниями не являются. Повествователь­ные предложения «Первое летописное упоминание о Москве было в 1812 г.», «Оперативное запоминающее устройство являет­ся внешней памятью компьютера» и «В компьютерном классе не надо соблюдать правила техники безопасности» являются выска­зываниями, поскольку это суждения, о каждом из которых мож­но сказать, что оно ложно. Истинными высказываниями будут суждения «Первое летописное упоминание о Москве было в 1147 г.», «Жесткий магнитный диск является внешней памятью компьютера».

Каждому высказыванию соответствует только одно из двух значений: или «истина», или «ложь», которые являются логиче­скими константами. Истинное значение принято обозначать цифрой 1, а ложное значение — цифрой 0. Высказывания можно обозначать с помощью логических переменных, в качестве кото­рых используются заглавные латинские буквы. Логические пере­менные могут принимать только одно из двух возможных значе­ний: «истина» или «ложь». Например, высказывание «Информа­ция в компьютере кодируется с помощью двух знаков» можно обозначить логической переменной А, а высказывание «Прин­тер является устройством хранения информации» можно обо­значить логической переменной В. Поскольку первое выска­зывание соответствует действительности, то А = 1. Такая запись означает, что высказывание А истинно. Так как второе высказы­вание не соответствует действительности, то В = 0. Такая запись означает, что высказывание в ложно.

Высказывания могут быть простыми и сложными. Высказывание называется простым, если никакая его часть не является высказыванием. До сих пор были приведены примеры простых высказываний, которые обозначались логическими перемены ми. Выстраивая цепочку рассуждений, человек с помощью логических операций объединяет простые высказывания в сложнее’ высказывания. Чтобы узнать значение сложного высказывания нет необходимости вдумываться в его содержание. Достаточно знать значение простых высказываний, составляющих сложное высказывание, и правила выполнения логических операций.

Логическая операция — действие, позволяющее составлять сложное высказывание из простых высказываний.

Все рассуждения человека, а также работа современных тех­нических устройств основываются на типовых действиях с ин­формацией — трех логических операциях: логическом отрица­нии (инверсии), логическом умножении (конъюнкции) и логи­ческом сложении (дизъюнкции).

Логическое отрицание простого высказывания получают до­бавлением слов «Неверно, что» в начале простого высказывания.

■ ПРИМЕР 1. Имеется простое высказывание «Крокодилы уме­ют летать». Результатом логического отрицания будет высказы­вание «Неверно, что крокодилы умеют летать». Значение ис­ходного высказывания — «ложь», а значение нового — «истина».

■ ПРИМЕР 2. Имеется простое высказывание «Файл должен иметь имя». Результатом логического отрицания будет высказы­вание «Неверно, что файл должен иметь имя». Значение исход­ного высказывания — «истина», а значение нового высказыва­ния — «ложь».

Можно заметить, что логическое отрицание высказывания истинно, когда исходное высказывание ложно, и наоборот, ло­гическое отрицание высказывания ложно, когда исходное вы­сказывание истинно.

Логическое отрицание (инверсия) — логическая операция, ставящая в соответствие простому высказыванию новое высказывание, значение которого противоположно значе­нию исходного высказывания.

Обозначим простое высказывание логической переменной А. Тогда логическое отрицание этого высказывания будем обозначать НЕ А. Запишем все возможные значения логической переменной А и соответствующие результаты логического отрицания НЕ А в виде таблицы, которая называется таблицей истинности для логичес­кого отрицания (табл. 40).

ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО ОТРИЦАНИЯ

Если/1 = 0, то НЕ А = 1 (см. пример 1).

Если А = 1, то НЕ А = 0 (см. пример 2)

Можно заметить, что в таблице истинности для логическо­го отрицания ноль меняется на единицу, а единица меняется на ноль.

Логическое умножение двух простых высказываний получа­ют объединением этих высказываний с помощью союза и. Разбе­рем на примерах 3—6, что будет являться результатом логическо­го умножения.

■ ПРИМЕР 3. Имеются два простых высказывания. Одно выска­зывание — «Карлсон живет в подвале». Другое высказывание — «Карлсон лечится мороженым».

Результатом логического умножения этих простых высказы­ваний будет сложное высказывание «Карлсон живет в подвале, и Карлсон лечится мороженым». Можно сформулировать новое высказывание более кратко: «Карлсон живет в подвале и лечится мороженым». Оба исходных высказывания ложны. Значение но­вого сложного высказывания также «ложь».

■ ПРИМЕР 4. Имеются два простых высказывания. Первое вы­сказывание — «Карлсон живет в подвале». Второе высказыва­ние — «Карлсон лечится вареньем».

Результатом логического умножения этих простых выска­зываний будет сложное высказывание «Карлсон живет в подва­ле и лечится вареньем». Первое исходное высказывание ложно, а второе истинно. Значение нового сложного высказывания — «ложь».

■ ПРИМЕР 5. Имеются два простых высказывания. Первое вы­сказывание — «Карлсон живет на крыше». Второе высказыва­ние — «Карлсон лечится мороженым».

Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится мороженым». Первое исходное высказывание истин но, а второе ложно. Значение нового сложного высказывания «ложь».

Результатом логического умножения этих простых высказываний будет сложное высказывание «Карлсон живет на крыше и лечится вареньем». Оба исходных высказывания истинны. Зпачение нового сложного высказывания также «истина».

Можно заметить, что логическое умножение двух высказываний истинно только в одном случае — когда оба исходных высказывания истинн ы.

Логическое умножение (конъюнкция) — логическая опера­ция, ставящая в соответствие двум простым высказывани­ям новое высказывание, значение которого истинно тогда и только тогда, когда оба исходных высказывания истинны.

ТАБЛИЦА ИСТИННОСТИ ДЛЯ ЛОГИЧЕСКОГО УМНОЖЕНИЯ

Источник

Основы математической логики

Исчисление высказываний

Тождественно истинными являются высказывания, которые не требуют задания каких-либо дополнительных условий для проверки своей истинности на протяжении всего процесса логического вывода.

Например, высказывание «кислород является газом» имеет значение ИСТИНА (1) в тех условиях, в которых оно рассматривается. Ведь кислород может находиться не только в газообразном состоянии.

Поэтому обязательным условием правильности выводов и следствий является то, чтобы постоянное высказывание, подобно константе, не меняло значение истинности в процессе логического вывода.

В исчислении высказываний не интересуются внутренней смысловой структурой элементарных высказываний. Естественно поэтому для их обозначения использовать отдельные буквы некоторого алфавита (обычно латинского и готического). Отдельными буквами могут обозначаться и так называемые переменные высказывания, что означает, что вместо этой буквы всегда может быть подставлено любое конкретное постоянное высказывание, как истинное, так и ложное.

Задача выделения тождественно истинных высказываний во множестве всех возможных высказываний является важнейшей задачей любого логического исчисления.

После всех предварительных замечаний перейдём к построению собственно исчисления высказываний, или, как его ещё иногда называют, пропозиционного исчисления.

Введём базовые операции.

В табл. 3.2 сведены соотношения истинности для базовых операций.

Таблица 3.2. Таблица истинности базовых операций

А	В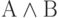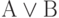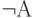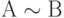
1	1	1	1	1	0	1
1	0	0	1	0	0	0
0	1	0	1	1	1	0
0	0	0	0	1	1	1

Как и в булевой алгебре введём ранжирование операций: .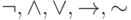

Например, формула понимается как . Формула должна пониматься как и т.д.

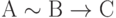
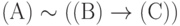
Введённые определения решают лишь две части задачи построения исчисления высказываний: проблему формализации записи сложных высказываний.

Тогда каждую формулу исчисления высказываний можно интерпретировать как формулу в булевой алгебре с включённой в неё дополнительно операцией импликации . Входящие в формулу постоянные высказывания должны быть заменены соответствующими булевыми константами (значениями их функций истинности). Символы, соответствующие переменным высказываниям, рассматриваются как аргументы булевой функции, представляемой формулой . Эта функция называется функцией истинности сложного высказывания, выражаемого формулой .

На содержательном уровне построения исчисления высказываний тождественно истинными считаются те, и только те формулы этого исчисления (сложные высказывания), функции истинности которых принимают значения ИСТИНА (1) при всех значениях переменных.

Представленный содержательный аспект исчисления высказываний позволяет сравнительно просто решить вопрос о тождественной истинности любого сложного высказывания: достаточно перебрать все возможные наборы значений истинности составляющих его переменных высказываний и проверить, на всех ли этих наборах функция истинности рассматриваемого сложного высказывания принимает значение ИСТИНА.

Например, рассмотрим формулу и составим для неё таблицу истинности с учётом «промежуточного» результата :

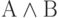
А	В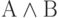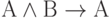
0	0	0	1
0	1	0	1
1	0	0	1
1	1	1	1

Видим, что при всех значениях переменных высказываний, сложное высказывание является истинным. Следовательно, рассмотренная формула тождественно истинная.

Несмотря на простоту и «прозрачность», содержательный аспект исчисления высказываний имеет ряд недостатков:

При формальном подходе к установлению тождественной истинности пользуются эквивалентными преобразованиями булевой алгебры. Поскольку там нет импликации, исключим её согласно равенству:

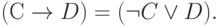( 3.24)

Проверим его справедливость с помощью таблицы истинности:

С	D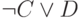
0	0	1	1
0	1	1	1
1	0	0	0
1	1	1	1

Рассмотрим тот же пример:

Эта цепочка доказывает тождественную истинность заданной формулы.

Таким образом, формальный аспект исчисления высказываний характеризуется тем, что полностью отвлекаются от содержательного смысла формул и рассматривают их как конечные последовательности символов, подлежащие эквивалентным преобразованиям.

Для этих преобразований, подобно и в дополнение базовому набору соотношений булевой алгебры, известна наиболее употребительная система аксиом С.К. Клини:

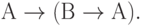( 3.25)

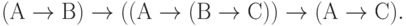( 3.26)

( 3.27)

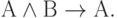( 3.28)

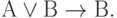( 3.29)

( 3.30)

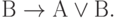( 3.31)

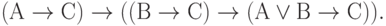( 3.32)

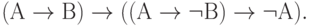( 3.33)

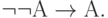( 3.34)

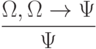( 3.35)

Первые десять аксиом представляют собой десять формул исчисления высказываний, объявленных тождественно истинными по определению. Они предполагают возможность подстановки вместо букв А, В, С любых формул исчисления высказываний (не обязательно истинных). Такая подстановка, по определению, не нарушает тождественной истинности аксиомы.

Формула называется непосредственным следствием формул и .

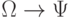
Формулы, тождественно истинные в содержательном смысле, для краткости будем называть просто содержательно истинными, противопоставляя их формально истинным, т.е. формально доказуемым.

Более точно это означает последовательное использование трёх условий, лежащих в основе правил вывода:

Цепочка формул, получающихся в результате последовательного применения этих трёх правил, которая кончается формулой , называется формальным выводом этой формулы.

Приведём простейшие примеры формального вывода, нумеруя последовательные шаги.

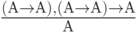( 3.36)

Приведённая цепочка формул по определению является формальным доказательством формулы . Таким образом, эта формула принадлежит к числу формально истинных формул, и её можно записать

Другим примером является получение следствий из трёх условно истинных формул 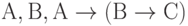. За пять шагов из этих формул может быть получена формула С.

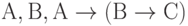
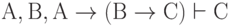
Таким образом, формула С выводима из формул и мы можем записать .

Хотя условно истинные формулы и не обладают тождественной истинностью, легко видеть, что в окончательной записи (условной) выводимости любая буква может быть заменена произвольной формулой, если только такая замена производится как слева, так и справа от знака .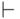

Подобным же способом можно доказать соотношения:

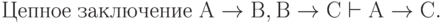( 3.37)

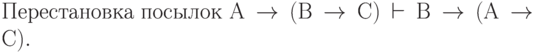( 3.38)

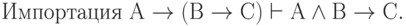( 3.39)

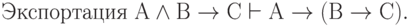( 3.40)

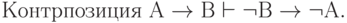( 3.41)

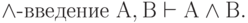( 3.42)

( 3.43)

Обозначим произвольную конечную совокупность формул исчисления высказываний. Применяя более сложную технику доказательства (индукцию по длине вывода), можно доказать следующую теорему о дедукции.

В теории доказательств часто применяются две общие схемы.

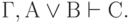( 3.44)

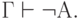( 3.45)

Из таблицы истинности для импликации непосредственно следует, что из содержательной истинности формул и вытекает содержательная истинность формулы . Но тогда очевидно, что все доказуемые (формально истинные) формулы будут и содержательно истинными. Верно (хотя и гораздо сложнее доказуемо) также и обратное, что формулируется следующей теоремой.

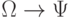
Теорема 2 содержит в себе два утверждения относительно выбранной системы аксиом: эта система содержательно непротиворечива и эта система содержательно полна, т.е. нет ни одной содержательно истинной формулы исчисления высказываний, которую нельзя было бы доказать формально с помощью этой системы аксиом.

При этом, естественно называть систему аксиом формально непротиворечивой, если с её помощью нельзя вывести какую-нибудь формулу вместе с её отрицанием ; в противном случае она формально противоречива.

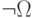
Отметим, что хотя присоединение недоказуемых формул в качестве новых аксиом исчисления высказываний, нарушает свойство формальной непротиворечивости, ничто не мешает нам присоединить к системе аксиом формулы в качестве не тождественно, а лишь условно истинных формул. (Это характерно, например, при переходе в мир грёз или сказок.) Противоречие возникает тогда и только тогда, когда конъюнкция является тождественно ложной формулой.

Источник