результат экспертизы можно считать приемлемым если значение коэффициента кендалла превышает
Any People’s blog
Коэффициент конкордации Кендалла или по-другому Коэффициент множественной ранговой корреляции нужен для того, чтобы выявить согласованность мнений экспертов по нескольким факторам.
Например, провели вы исследование, в котором попросили 5 человек проранжировать по важности 4 разных фактора. Они вам расставили ранги от 1 до 4 и вам теперь надо это анализировать. Вот тут то и может понадобиться Коэффициент конкордации К ендалла.
Способ расчета Коэфициента конкордации Кендалла.

Разберем на примере, в котором 5 экспертов оценили 4 фактора.
Остается найти сумма квадратов разностей рангов (S).
Её можно найти по любой из следующих формул:
Для вычисления нам нужно добавить пару новых строк в исходную таблицу (Сумма по столбцу и Квадрат этой суммы).
По формуле (2) получаем:
По формуле (3) получаем:
Теперь считаем, собственно говоря, сам коэфициента конкордации Кендалла по формуле (1):
Расчеты из данного примера в Экселе можно скачать тут.
Слабая согласованность обычно является следствием следующих причин:
Пример расчета коэффициент корреляции Кендалла
Для одного класса в 14 учащихся нам известны результаты их уровня интеллекта (IQ) и время решения серии логических заданий (X).
| № | Уровень интеллекта (IQ) | Время решения логических задач в секундах (X) |
| 1 | 100 | 154 |
| 2 | 118 | 123 |
| 3 | 112 | 120 |
| 4 | 97 | 213 |
| 5 | 99 | 200 |
| 6 | 103 | 187 |
| 7 | 102 | 155 |
| 8 | 132 | 100 |
| 9 | 122 | 114 |
| 10 | 121 | 115 |
| 11 | 115 | 107 |
| 12 | 117 | 176 |
| 13 | 109 | 143 |
| 14 | 111 | 111 |
1. Проранжируем полученные данные по столбцу IQ
| № | IQ | X |
| 4 | 1 | 14 |
| 5 | 2 | 13 |
| 1 | 3 | 9 |
| 7 | 4 | 10 |
| 6 | 5 | 12 |
| 13 | 6 | 8 |
| 14 | 7 | 3 |
| 3 | 8 | 6 |
| 11 | 9 | 2 |
| 12 | 10 | 11 |
| 2 | 11 | 7 |
| 10 | 12 | 5 |
| 9 | 13 | 4 |
| 8 | 14 | 1 |
2. Вычислим число совпадений значений P(p).
Например,
для первого испытуемого число совпадений будет равно 0, поскольку ранг второго испытуемого по столбцу X меньше, чем ранг первого испытуемого, следовательно у них нет совпадающих между собой рангов.
для третьего испытуемого число совпадений будет 1, поскольку если из ранга четвертого испытуемого по столбцу X вычесть ранг третьего испытуемого, разность будет равна 1, следовательно количество совпадающих рангов 1.
2.1. Заполняем столбец с числом совпадений для каждого испытуемого:
| № | Число совпадений P(p) |
| 4 | 0 |
| 5 | 0 |
| 1 | 1 |
| 7 | 2 |
| 6 | 0 |
| 13 | 0 |
| 14 | 3 |
| 3 | 0 |
| 11 | 9 |
| 12 | 0 |
| 2 | 0 |
| 10 | 0 |
| 9 | 0 |
| 8 | 0 |
| Сумма P(p) | 15 |
3. Подсчитываем сумму совпадающих значений P(p).
3.1. Вычислить сумму инверсий можно применив формулу:
Результат экспертизы можно считать приемлемым если значение коэффициента кендалла превышает
РАЗДЕЛ 1. МЕТОД ЭКСПЕРТНЫХ ОЦЕНОК. МЕТОД ДЕЛЬФИ.
ИСПОЛЬЗОВАНИЕ «МЕТОДОВ ЭКСПЕРТНЫХ ОЦЕНОК».
Использование информации, полученной от специалистов, особенно плодотворно, если для ее сбора, обобщения и анализа применяются специальные логические приемы и математические методы – методы экспертных оценок. Экспертный метод в значительной мере может обеспечить объективность, многосторонность, комплексность и компетентность принимаемых практических решений. На сегодня этот метод достаточно разработан и применяется у нас и за рубежом как средство повышения надежности решения научных и управленческих проблем. Однако следует помнить, что он не должен быть единственным основанием для принятия решений и должен сопровождаться сопоставлением с объективной информацией, полученной другими методами.
При решении сложных проблем один специалист не в состоянии учесть все факторы и взаимосвязи между ними или оценить вероятности большого числа альтернатив. Поэтому групповые экспертизы получили широкое распространение. Преимуществом их является возможность разностороннего анализа количественных и качественных аспектов сложных проблем. Примером таких проблем являются прогнозы в области политики, науки и техники, для обоснования которых нет адекватной информации.
При использовании мнений группы специалистов предполагается, что взаимодействие между ними позволит скомпенсировать смещение оценок отдельных членов группы и что сумма информации, имеющейся в распоряжении группы экспертов, будет больше, чем информация любого члена группы. Очевидно также, что сумма факторов, которые имеют отношение к данной проблеме и могут быть рассмотрены группой экспертов, как правило, больше или, по крайней мере, так же велика, как сумма факторов, которые может учесть отдельный эксперт.
В общем случае мнение группы экспертов надежнее, чем мнение отдельного индивида, а две группы одинаково компетентных экспертов с большей вероятностью дадут аналогичные ответы на ряд вопросов, чем два индивида. Предполагается также, что интервал оценок, полученных от группы экспертов, включает в себя «истинную» оценку. Эти предположения не очевидны, особенно если учесть проблемы групповой динамики. К примеру, мнения специалистов, даже работающих в одной узкой области, могут расходиться. Более того, и однозначность ответов не является гарантией их обоснованности. Во всяком случае, нет способа проверить это в момент проведения экспертизы. Можно предположить, что взятое наудачу мнение любого из экспертов будет так же достоверно, как и групповая оценка, поскольку никто не может заранее сказать, каков «истинный» результат. В то же время основное преимущество групповой оценки заключается в уменьшении различий во мнениях, в возможности получения более обобщенного, более представительного мнения. Сочетание индивидов, обладающих разными стилями мышления, несомненно, позволяет повысить надежность решения задач. В то же время, очевидно, что количество неверной информации у группы экспертов будет больше или, по крайней мере, такое же, как и у одного из них. Немалое влияние на надежность решений может оказывать также групповой конформизм.
Экспериментально установлено, что, несмотря на эти недостатки, групповые оценки более надежны, чем индивидуальные, при условии соблюдения определенных требований, важнейшими из которых являются:
а) приемлемое «гладкое» распределение оценок, полученное от экспертов, указывающее на независимость их мнений. В случае многомодального распределения должна быть установлена причина, по которой различные эксперты по-разному интерпретируют одну и ту же проблему;
б) групповая надежность, означающая, что две групповые оценки по определенной проблеме, данные двумя одинаковыми подгруппами, выбранными случайным образом, будут близкими. Корреляция по ряду таких оценок должна быть высокой.
ЧТО ТАКОЕ «ЭКСПЕРТНАЯ ОЦЕНКА»?
Экспертные оценки – это качественные оценки, основанные на информации неколичественного (качественного) характера, которые могут быть получены только с помощью специалистов – экспертов. Эксперт – это высококвалифицированный специалист, полагающийся на свои знания, опыт, интуицию и умение оценивать сложные факторы (явления) и способный создать собственную обоснованную (интуитивную) модель анализируемого явления (проблемы), если он располагает необходимой для этого исходной информацией.
В ЧЕМ СОСТОИТ СУЩНОСТЬ МЕТОДА ЭКСПЕРТНОГО ОЦЕНИВАНИЯ?
Метод экспертного оценивания относится к инструментарию количественной оценки качества альтернатив в условиях слабоформализуемой проблемной ситуации. Сущность метода экспертных оценок заключается в логико-интуитивном анализе внутренней и внешней среды организации, разработке альтернатив и количественной оценке их качества. Обобщенное мнение экспертов служит основанием для осуществления выбора.
КАКИЕ ТИПОВЫЕ ЗАДАЧИ РЕШАЮТСЯ МЕТОДОМ ЭКСПЕРТНОГО ОЦЕНИВАНИЯ?
Методом экспертного оценивания решаются следующие типовые задачи:
1) определение состава возможных событий в какой-либо системе в определенном интервале времени;
2) определение вероятностей событий и временных интервалов во множестве событий;
3) структурирование проблемного поля организации и определение приоритетности решения проблем;
4) дифференциация целей управления до задач и определение приоритетности их решения;
5) генерирование альтернатив;
6) фильтрация множества альтернатив и оценка их предпочтительности.
ЧТО ТАКОЕ ЭКСПЕРТНЫЕ СУЖДЕНИЯ?
Экспертные суждения – содержательные высказывания (определяющие состав, структуру, функциональность исследуемой системы, сущностей и их атрибутов), количественная или качественная оценка какой-либо сущности (т.е. определение количественных и качественных атрибутов и их значений).
В ЧЕМ ЗАКЛЮЧАЕТСЯ СУЩНОСТЬ ЭКСПЕРТНОГО РАНЖИРОРАНИЯ?
Экспертное ранжирование применяется в случаях, когда невозможна или нецелесообразна непосредственная оценка. При этом ранжирование объектов содержит лишь информацию о том, какой из них более предпочтителен, и не содержит информации о том, насколько или во сколько раз один объект предпочтительнее другого.
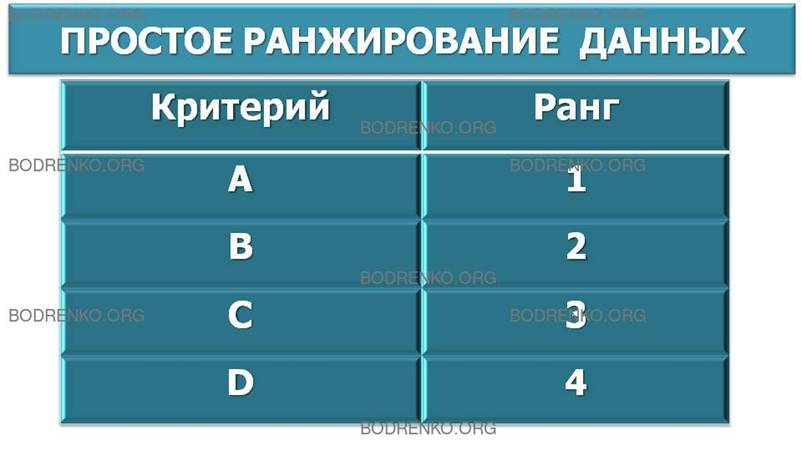
Ранг – степень отличия по какому-либо признаку, а ранжирование – процесс определения рангов, относительных количественных оценок степеней отличий по качественным признакам.
КАКИЕ ОСНОВНЫЕ МЕТОДЫ РАНЖИРОВАНИЯ ИСПОЛЬЗУЮТСЯ?
Используются следующие основные методы ранжирования: МЕТОД ПРОСТОЙ РАНЖИРОВКИ; МЕТОД НЕПОСРЕДСТВЕННОЙ ОЦЕНКИ; МЕТОД ПАРНЫХ СРАВНЕНИЙ, МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРЕДПОЧТЕНИЙ.
В ЧЕМ ЗАКЛЮЧАЕТСЯ МЕТОД ПРОСТОЙ РАНЖИРОВКИ?
При решении многих практических задач часто оказывается, что факторы, определяющие конечные результаты, не поддаются непосредственному измерению. Расположение этих факторов (альтернатив) в порядке возрастания или убывания какого-либо присущего им свойства называется ранжированием. Нередко рассматриваемые явления имеют различную природу и в связи с этим несоизмеримы. В этих случаях установление их относительной значимости с помощью экспертов и присвоение чисел натурального ряда, определяющих порядок (место) каждого явления в исследуемой совокупности, облегчает выбор наиболее предпочтительной из альтернатив.
Следует иметь в виду, что ранги, присвоенные объектам, не являются числовой мерой изучаемого качества. Ранги представляют собой только символы, указывающие предпочтения одного объекта перед другим. Поэтому к математическим операциям с ними надо подходить с большой осторожностью. Некоторые специалисты считают задачу количественной оценки качественного признака некорректной и полагают, что измерение качественного признака возможно только в номинальной или порядковой шкале. Однако на практике количественные оценки качественных признаков широко и достаточно успешно применяются. Они используются для оценки предпочтительности альтернатив при подготовке решений, для оценки важности позиций плана, при решении задачи оптимального распределения по этим позициям ограниченных ресурсов и т.д.
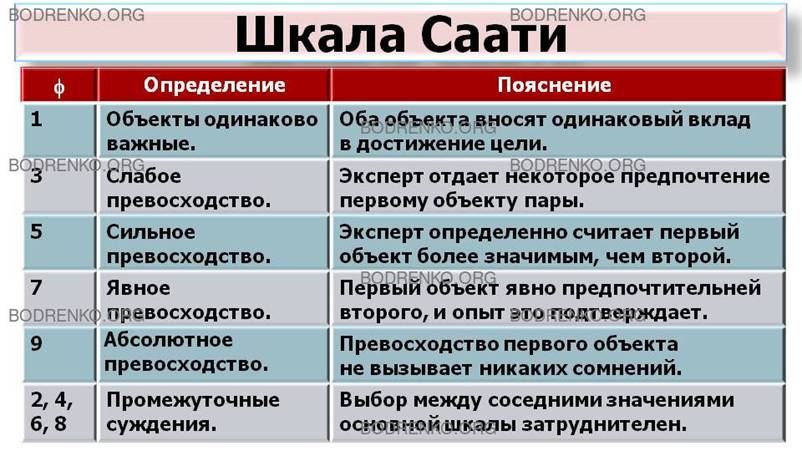
ЧТО ТАКОЕ «ШКАЛА СААТИ»?
В литературе рассматриваются различные шкалы для измерения степени превосходства f одного объекта над другим, например шкала Т. Саати, представленная в таблице 1.
Объекты одинаково важные.
Оба объекта вносят одинаковый вклад в достижение цели.
Эксперт отдает некоторое предпочтение первому объекту пары.
Эксперт определенно считает первый объект более значимым, чем второй.
Первый объект явно предпочтительней второго, и опыт это подтверждает.
Превосходство первого объекта не вызывает никаких сомнений.
Значения, соответствующие промежуточным суждениям.
Для случаев, когда выбор между соседними значениями основной шкалы вызывает затруднения.
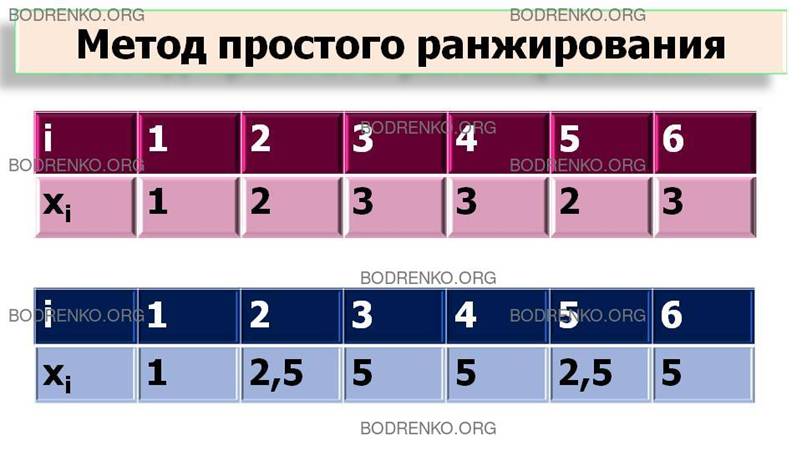
Порядковая шкала, получаемая в результате ранжирования, должна удовлетворять условию равенства числа рангов N числу ранжируемых объектов n. Однако бывает, что эксперт не в состоянии указать порядок следования для двух или нескольких объектов или присваивает разным объектам один и тот же ранг. В таких случаях объектам присваивают так называемые стандартизованные ранги. Для этого общее число стандартизированных рангов полагают равным n, а объектам, имеющим одинаковые ранги, присваивают стандартизованный ранг, значение которого представляет собой среднее значение суммы мест, поделенных между собой объектами с одинаковыми рангами.
Пусть, например, шести альтернативам присвоены следующие ранги:
Тогда альтернативам 2 и 5, поделившим между собой второе и третье места, присваивается стандартизованный ранг S = (2 + 3)/2 = 2,5, а альтернативам 3, 4 и 6, поделившим 4, 5 и 6 места, присваивается стандартизованный ранг S = (4+5+6)/3 = 5.
В итоге получаем следующую нормальную ранжировку:
где xi – ранг i-го объекта.
При ранжировании рационально сначала выделить самую важную переменную, приписав ей вес 100, и наименее важную, по возможности, также указав ее вес. Затем путем попарного сравнения присвоить ранги всем переменным одной группы. В случае, когда ряду переменных присвоены одинаковые ранги, следует дополнительно определить стандартизованные ранги.
Метод ранжирования редко используется в чистом виде. Обычно его сочетают с другими методами, облегчающими различимость альтернатив для экспертов. К примеру, сначала может быть произведена оценка величин, а уж затем их ранжирование. Для установления более тесной связи между оценками, приписываемыми экспертами отдельным объектам, их зачастую нормируют. Нормирование любой меры означает, что представляющее ее число для всего множества в целом принимается равным единице. Для нормирования каждой конкретной оценки сначала суммируются оценки по всем объектам, а затем каждая из них делится на полученную сумму. Когда в экспертизе участвуют несколько экспертов, обычно стремятся получить усредненную оценку (вес) для каждого объекта. Для этого нормированные оценки каждого объекта суммируются, а затем полученная сумма делится на число экспертов.
В ЧЕМ ЗАКЛЮЧАЕТСЯ МЕТОД НЕПОСРЕДСТВЕННОЙ ОЦЕНКИ?
Метод непосредственной оценки заключается в отнесении объекта оценки к определенному значению по оценочной шкале. То есть в присвоении объекту оценки определенного количества баллов в определенном интервале, например, от 0 до 10 – в соответствии с предпочтением по какому-либо признаку или их группе (альтернативы, например, оцениваются по предпочтению; критерии – по значимости; факторы внешней среды – по оказываемому влиянию; проблемы – по приоритетности решения).
В ЧЕМ ЗАКЛЮЧАЕТСЯ СУЩНОСТЬ МЕТОДА ПАРНЫХ СРАВНЕНИЙ?
Метод парных сравнений. Точность и надежность процедуры ранжирования сильно зависит от количества объектов ранжирования. Чем меньше таких объектов, тем легче эксперту их различать. Поэтому количество ранжируемых объектов не должно быть больше 20, а желательно, чтобы их было меньше 10. При малом числе объектов возможно их непосредственное ранжирование, а при числе объектов 7 ± 2 эксперт может иметь заметные трудности в выборе наилучшего объекта. Дело в том, что человек в состоянии выбрать наилучший объект, не прибегая к парным сравнениям только когда число объектов не больше емкости его кратковременной памяти, которая не превышает 9 единиц информации. Иначе результат непосредственного ранжирования становится ненадежным.
При большом числе объектов интуитивные оценки экспертов становятся ненадежными, и приходится прибегать к формализованным процедурам экспертного оценивания. В этом случае эксперт должен представить для дальнейшей обработки результаты проведенных им парных сравнений объектов. В зависимости от типа решаемой задачи эксперт должен либо определить более предпочтительный объект каждой рассматриваемой пары (или признать объекты пары равноценными по рассматриваемому признаку), либо указать, во сколько раз один из объектов предпочтительнее другого. Полученная таким образом исходная информация обрабатывается формальными логически обоснованными методами. Сравнивая два объекта, эксперт может определить более предпочтительный из них, либо признать эти объекты эквивалентными. В методе парных сравнений от эксперта не требуется последовательности в суждениях, т.е. предпочтения эксперта не обязательно должны быть транзитивными. Это условие особенно существенно при большом числе оцениваемых объектов, когда эксперту даже при желании трудно запомнить высказанные им ранее суждения о предпочтениях. Нетранзитивность экспертных предпочтений отнюдь не является редким событием Установлено, что число таких суждений велико и может достигать 30% от их общего количества, особенно при сравнении нечетких множеств. Основная причина этого явления заключается в способе мышления человека, который обычно стремится заменить сложную проблему последовательностью более простых задач. Выбор по сложному качественному признаку также может быть представлен как выбор по совокупности нескольких более простых признаков. А далее может происходить следующее: эксперт, сравнивая одну пару объектов, принимает за решающий один частный признак, а сравнивая другую пару объектов, может посчитать более важным другой частный признак. Это и приводит к противоречивости его суждений.
ЧТО ТАКОЕ МАТРИЦА ПАРНЫХ СРАВНЕНИЙ?
При использовании метода парных сравнений составляется матрица парных сравнений. Метод парных сравнений заключается в определении предпочтений элементов, расположенных в левом столбце, над элементами, расположенными в верхней строке составляемой таблицы (матрицы парных сравнений). При использовании данного метода составляется матрица, по строкам и столбцам которой располагают сравниваемые объекты. В этом методе ранги объектов подсчитывают после составления матрицы. Рассмотрим пример составления матрицы парных сравнений для четырех объектов A 1, A 2, A 3, A 4 (таблица 2) и вычислим их ранги.
Русские Блоги
Три статистических коэффициента корреляции (пирсон, копейщик, кендалл)
(Перевод из публичного аккаунта WeChat Crick Academy)
1. коэффициент корреляции личности (коэффициент корреляции Пирсона)
Формула выглядит следующим образом:
Знаменателем формулы является стандартное отклонение переменной, что означает, что при вычислении коэффициента корреляции Пирсона стандартное отклонение переменной не может быть 0 (знаменатель не может быть 0), что означает, что значения любого из ваши две переменные не могут быть одинаковыми. Если изменений нет, коэффициент корреляции Пирсона нельзя использовать для расчета, коррелирует ли эта переменная с другой переменной.
Это похоже на то, что мы хотим изучить корреляцию между скоростью бега людей и сердцебиением. Если вы бежите быстро, ваше сердцебиение не изменится (то есть стандартное отклонение переменной сердцебиения равно 0) или если ваше сердцебиение колеблется быстро и медленно, но Всегда поддерживая скорость во время бега (то есть стандартное отклонение переменной скорости бега равно 0), тогда мы не можем судить, связано ли сердцебиение со скоростью бега, вычисляя коэффициент корреляции Пирсона.
Давайте поднимемся немного выше и рассмотрим более общий пример. Для выполнения вычислений мы используем популярный язык R. Если у вас также есть язык R, вы можете сделать это вместе:
Предположим, вы провели биологический эксперимент и вас устраивают следующие две переменные:
Y1=c(0.3, 0.9, 2.7, 2, 3.5, 5)
> Y1《-c(0.3, 0.9, 2.7, 2, 3.5, 5)
> sd (X1) # стандартное отклонение
> cov (X1, Y1) # ковариация
> cor (X1, Y1, method = «pearson») # коэффициент корреляции Пирсона
Его значение выше 0,9, что указывает на то, что они очень связаны.Например, было подтверждено, что изменение экспрессии протеина А имеет большую взаимосвязь с изменением экспрессии протеина В! Вы можете быть очень счастливы получить этот статистически подтвержденный результат.
In cor(X2, Y1, method = «pearson») : the standard deviation is zero
R-прогоны получат пропущенное значение (NA), и код напоминает вам: стандартное отклонение равно нулю (попробуйте вычислить стандартное отклонение X2 самостоятельно), затем поймите значение вышеизложенного! Другими словами, значение в X2 вообще не колеблется, и корреляция между ним и Y1 не может быть вычислена этим методом.
Во-первых, обычно предполагается, что экспериментальные данные представляют собой парную популяцию из нормального распределения. Почему обычно предполагается нормальное распределение? Поскольку после того, как мы находим коэффициент корреляции Пирсона, мы обычно используем t-критерий и другие методы для проверки коэффициента корреляции Пирсона, а t-критерий основан на предположении, что данные распределены нормально.

Во-вторых, разрыв между экспериментальными данными не может быть слишком большим, иначе на коэффициент корреляции Пирсона сильно влияют выбросы. Например, в примере с сердцебиением и бегом только что, если сердце человека не очень хорошее, он не может его переносить после бега с определенной скоростью и у него сердечный приступ. В этот раз мы измерим сердцебиение. который отклоняется от нормального значения (слишком быстро или слишком медленно), даже 0), если мы поместим это значение в корреляционный анализ, его наличие сильно повлияет на результат расчета.
2. коэффициент корреляции Спирмена

Введите формулу для получения коэффициента корреляции Спирмена: ρs = 1-6 * (1 + 1 + 1 + 9) /6*35=0.657
Другими словами, нас не волнует разница между конкретными значениями двух переменных X и Y. Нам нужно только вычислить разницу в расположении каждого из их значений, чтобы найти коэффициент корреляции. Теперь это легче понять? По-прежнему используйте приведенные выше данные, запишите приведенный ниже код, чтобы добиться:
Более того, даже если значение переменной не изменится, не будет ситуации, когда знаменатель равен 0 и его нельзя будет вычислить, как коэффициент Пирсона. Кроме того, даже если есть выбросы, поскольку ранг выбросов обычно существенно не меняется (например, если они слишком большие или слишком маленькие, они будут ранжироваться либо первым, либо последним), поэтому влияние на коэффициент корреляции Спирмена будет тоже очень маленький!
Поскольку коэффициент корреляции Спирмена не имеет этих требований к условиям данных, сфера применения намного шире. В нашем анализе данных биологического эксперимента, особенно при анализе данных кроссовера нескольких омиков, частота использования очень высока при объяснении корреляции между различными данными омикс.
3. Коэффициент корреляции Кендалла (коэффициент корреляции Кендалла)
Коэффициент корреляции Кендалла, также известный как коэффициент ранговой корреляции Кендалла, также является коэффициентом ранговой корреляции, но объект, который он вычисляет, является категориальными переменными.
Категориальные переменные можно понимать как категориальные переменные, которые можно разделить на
Беспорядочно, Такие как пол (мужской, женский), группа крови (A, B, O, AB);
Упорядоченный, Например, уровень ожирения (сильно ожирение, умеренное ожирение, умеренное ожирение, не ожирение).
Обычно все коэффициенты корреляции являются упорядоченными категориальными переменными.
Из-за различных условий данных формулы расчета для получения коэффициента корреляции Кендалла различаются. Как правило, существует три формулы расчета. Формулы расчета здесь не утомительно перечислены, а функции расчета языка R даны непосредственно:
В настоящее время можно понять, что взгляды двух учителей на игроков находятся в противоположных тенденциях, но степень противоположности не очень велика.