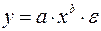03. Линейная модель парной регрессии и корреляции
Рассмотрим простейшую модель парной регрессии – Линейную Регрессию. Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
или 
. (1.1)
Уравнение вида позволяет по заданным значениям фактора X находить теоретические значения результирующего показателя, подставляя в него фактические значения фактора X.
Построение линейной регрессии сводится к оценке ее параметров – A и B. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров A и B, при которых сумма квадратов отклонений фактических значений результирующего показателя Y от теоретических 
минимальна:
. (1.2)
Т. е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 1.2):
Рис. 1.2. Линия регрессии с минимальной дисперсией остатков.
Как известно из курса математического анализа, чтобы найти минимум функции (1.2), надо вычислить частные производные по каждому из параметров A и B и приравнять их к нулю. Обозначая 
через 
, получим:
(1.3)
После несложных преобразований, получим следующую систему линейных уравнений для оценки параметров A и B:
(1.4)
Решая систему уравнений (1.4), найдем искомые оценки параметров A и B. Можно воспользоваться готовыми формулами, которые следуют непосредственно из решения системы (1.4):
, 
, (1.5)
Где 
– ковариация признаков X и Y, 
– дисперсия признака X и
, 
, 
, 
.
Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий. Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое Ожидание – сумма произведений значений случайной величины на соответствующие вероятности (см. Приложение 1).
Параметр B называется Коэффициентом Регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.
Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.
Формально A – значение Y при 
. Если фактор X не может иметь нулевого значения, то тогда трактовка свободного члена A не имеет смысла, т. е. параметр A может не иметь экономического содержания.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции 
, который можно рассчитать по следующим формулам:
. (1.6)
Линейный коэффициент корреляции находится в пределах: 
. Чем ближе абсолютное значение к единице, тем сильнее линейная связь между факторами (при 
имеем строгую функциональную зависимость). Однако близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 
, называемый Коэффициентом Детерминации. Коэффициент детерминации характеризует долю дисперсии результирующего показателя Y, объясняемую регрессией, в общей дисперсии результирующего показателя:
, (1.7)
Где 
, 
.
Соответственно величина 
характеризует долю дисперсии Y, вызванную влиянием остальных, не учтенных в модели, факторов.
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Проверить значимость уравнения регрессии – означает установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют Среднюю Ошибку Аппроксимации:
. (1.8)
Средняя ошибка аппроксимации не должна превышать 8–10%.
Оценка Значимости Уравнения Регрессии В целом Производится На Основе F—Критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.
Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной Y от среднего значения 
раскладывается на две части – «объясненную» и «необъясненную»:
,
Где 
– общая сумма квадратов отклонений; 
– сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений); 
– остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.
Схема дисперсионного анализа имеет вид, представленный в таблице 1.1 (N – число наблюдений, M – число параметров при переменной X).
Парная регрессия и корреляция
1. Наиболее наглядным видом выбора уравнения парной регрессии является:
в) экспериментальный (табличный).
2. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:
а) не менее 5 наблюдений;
б) не менее 7 наблюдений;
в) не менее 10 наблюдений.
3. Суть метода наименьших квадратов состоит в:
а) минимизации суммы остаточных величин;
б) минимизации дисперсии результативного признака;
в) минимизации суммы квадратов остаточных величин.
4. Коэффициент линейного парного уравнения регрессии:
а) показывает среднее изменение результата с изменением фактора на одну единицу;
б) оценивает статистическую значимость уравнения регрессии;
в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.
5. На основании наблюдений за 50 семьями построено уравнение регрессии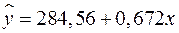 
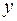
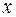
, где 
– потребление, 
– доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?
в) ничего определенного сказать нельзя.
6. Суть коэффициента детерминации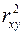 
состоит в следующем:
а) оценивает качество модели из относительных отклонений по каждому наблюдению;
б) характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака;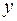
в) характеризует долю дисперсии 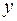, вызванную влиянием не учтенных в модели факторов.
7. Качество модели из относительных отклонений по каждому наблюдению оценивает:
а) коэффициент детерминации ;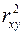
б)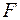 
-критерий Фишера;
в) средняя ошибка аппроксимации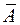 
.
8. Значимость уравнения регрессии в целом оценивает:
а) 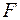-критерий Фишера;
б)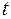 
-критерий Стьюдента;
в) коэффициент детерминации .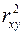
9. Классический метод к оцениванию параметров регрессии основан на:
а) методе наименьших квадратов:
б) методе максимального правдоподобия:
в) шаговом регрессионном анализе.
10. Остаточная сумма квадратов равна нулю:
а) когда правильно подобрана регрессионная модель;
б) когда между признаками существует точная функциональная связь;
11. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
а)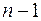 
;
б)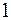 
;
в)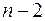 
.
12. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
а) ;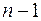
б) ;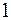
в) .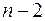
13. Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
а) ;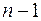
б) ;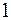
в) .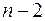
14. Для оценки значимости коэффициентов регрессии рассчитывают:
а) 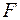-критерий Фишера;
б) 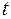-критерий Стьюдента;
в) коэффициент детерминации .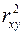
15. Какое уравнение регрессии нельзя свести к линейному виду:
а)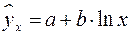 
;
б)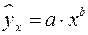 
:
в)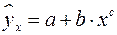 
.
16. Какое из уравнений является степенным:
а) ;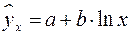
б) :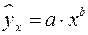
в) .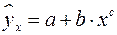
17. Параметр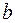 
в степенной модели является:
а) коэффициентом детерминации;
б) коэффициентом эластичности;
в) коэффициентом корреляции.
18. Коэффициент корреляции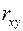 
может принимать значения:
19. Для функции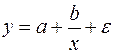 
средний коэффициент эластичности имеет вид:
а)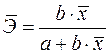 
;
б)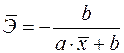 
;
в)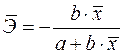 
.
20. Какое из следующих уравнений нелинейно по оцениваемым параметрам:
а)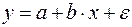 
;
б)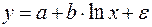 
;
в)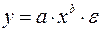 
.
Тестовые задания. Парная регрессия и корреляция
Парная регрессия и корреляция
1.Наиболее наглядным видом выбора уравнения парной регрессии является:
в) экспериментальный (табличный).
2.Рассчитывать параметры парной линейной регрессии можно, если у нас есть:
а) не менее 5 наблюдений;
б) не менее 7 наблюдений;
в) не менее 10 наблюдений.
3. Суть метода наименьших квадратов состоит в:
а) минимизации суммы остаточных величин;
б) минимизации дисперсии результативного признака;
в) минимизации суммы квадратов остаточных величин.
4. Коэффициент линейного парного уравнения регрессии:
а) показывает среднее изменение результата с изменением фактора на одну единицу;
б) оценивает статистическую значимость уравнения регрессии;
в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.
5. На основании наблюдений за 50 семьями построено уравнение регрессии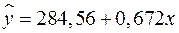 
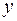
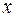
, где 
– потребление, 
– доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?
в) ничего определенного сказать нельзя.
6. Суть коэффициента детерминации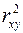 
состоит в следующем:
а) оценивает качество модели из относительных отклонений по каждому наблюдению;
б) характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака;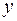
в) характеризует долю дисперсии 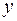, вызванную влиянием не учтенных в модели факторов.
7. Качество модели из относительных отклонений по каждому наблюдению оценивает:
а) коэффициент детерминации ;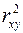
б)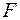 
-критерий Фишера;
в) средняя ошибка аппроксимации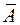 
.
8. Значимость уравнения регрессии в целом оценивает:
а) 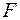-критерий Фишера;
б)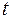 
-критерий Стьюдента;
в) коэффициент детерминации .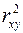
9. Классический метод к оцениванию параметров регрессии основан на:
а) методе наименьших квадратов:
б) методе максимального правдоподобия:
в) шаговом регрессионном анализе.
10. Остаточная сумма квадратов равна нулю:
а) когда правильно подобрана регрессионная модель;
б) когда между признаками существует точная функциональная связь;
11. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
а)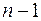 
;
б)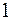 
;
в)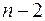 
.
12. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
а) ;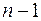
б) ;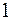
в) .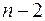
13. Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:
а) ;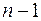
б) ;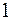
в) .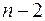
14. Для оценки значимости коэффициентов регрессии рассчитывают:
а) 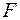-критерий Фишера;
б) 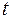-критерий Стьюдента;
в) коэффициент детерминации .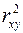
15. Какое уравнение регрессии нельзя свести к линейному виду:
а) 
;
б)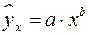 
:
в)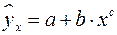 
.
16. Какое из уравнений является степенным:
а) ;
б) :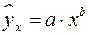
в) .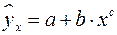
17. Параметр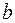 
в степенной модели является:
а) коэффициентом детерминации;
б) коэффициентом эластичности;
в) коэффициентом корреляции.
18. Коэффициент корреляции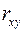 
может принимать значения:
19. Для функции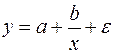 
средний коэффициент эластичности имеет вид:
а) 
;
б)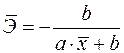 
;
в)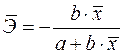 
.
20. Какое из следующих уравнений нелинейно по оцениваемым параметрам:
а)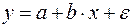 
;
б)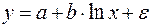 
;
в) 
.
