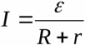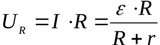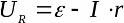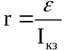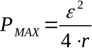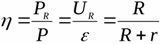Что такое внутреннее сопротивление

Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.

В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для гальванического элемента или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

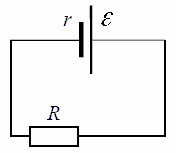
На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены ЭДС источника, его внутреннее сопротивление, а также сопротивление нагрузки. Согласно закону Ома для замкнутой цепи, ток в данной цепи будет равен:

Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

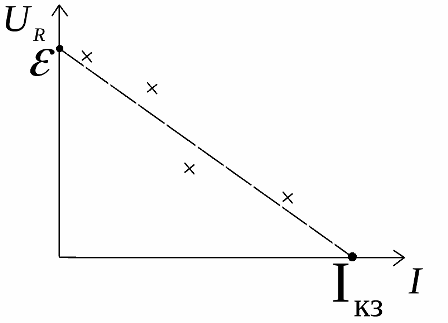
График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен току короткого замыкания. Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

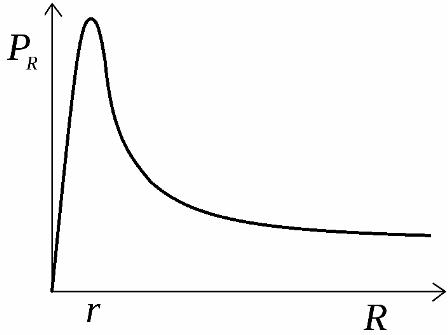
Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает источник:

Ясно, что если источник развивает такую мощность, что на нагрузке получается максимум возможной мощности для данного источника, то КПД источника окажется равным 50%.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Электрическое сопротивление.

Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.

Электрическое сопротивление определяется как коэффициент пропорциональности R между напряжением U и силой постоянного тока I в законе Ома для участка цепи.

Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом (1 Ом) — это сопротивление такого проводника, в котором при напряжении 1 В сила тока равна 1 А.

Удельное сопротивление.

Сопротивление однородного проводника постоянного сечения зависит от материала проводника, его длины l и поперечного сечения S и может быть определено по формуле:

,

Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.

Из формулы следует, что

,

Величина, обратная ρ, называется удельной проводимостью σ:

.

Зависимость сопротивлений от температуры.

С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.

Температурным коэффициентом сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на 1 °С к величине его сопротивления при 0 ºС:

.

Зависимость удельного сопротивления проводников от температуры выражается формулой:

.

Зависимость сопротивления проводника от температуры используется в термометрах сопротивления.

Источник

Закон Ома

Сопротивление

Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.

Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.

Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.

Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.

Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.

Эту закономерность можно описать следующей формулой:

Сопротивление

R = ρ l/S

R — сопротивление [Ом]

l — длина проводника [м]

S — площадь поперечного сечения [мм^2]

ρ — удельное сопротивление [Ом*мм^2/м]

Единица измерения сопротивления — Ом. Названа в честь физика Георга Ома.

Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм^2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм^2. При умножении мм^2 сокращаются и мы получаем величину в СИ.

Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм^2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм^2.

Таблица удельных сопротивлений различных материалов

Константан ( сплав Ni-Cu + Mn)

Нейзильбер (сплав меди цинка и никеля)

Никелин ( сплав меди и никеля)

Нихром ( сплав никеля хрома железы и марганца)

Резистор

Все реальные проводники имеют сопротивление, но его стараются сделать незначительным. В задачах вообще используют словосочетание «идеальный проводник», а значит лишают его сопротивления.

Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.

Вот так резистор изображается на схемах:

В школьном курсе физики используют Европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.

Вот так резистор выглядит в естественной среде обитания:

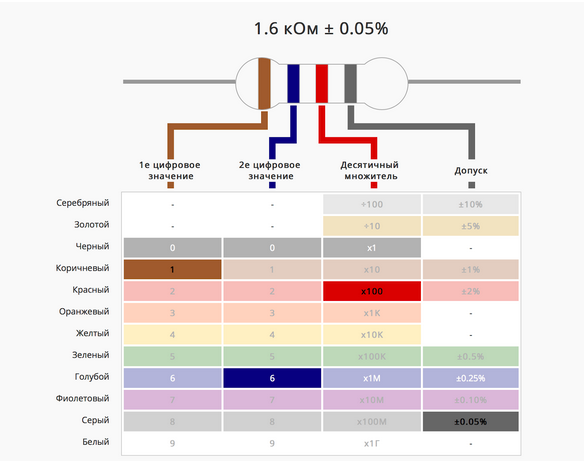
Полосочки на нем показывают его сопротивление.

На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:

О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.

Реостат

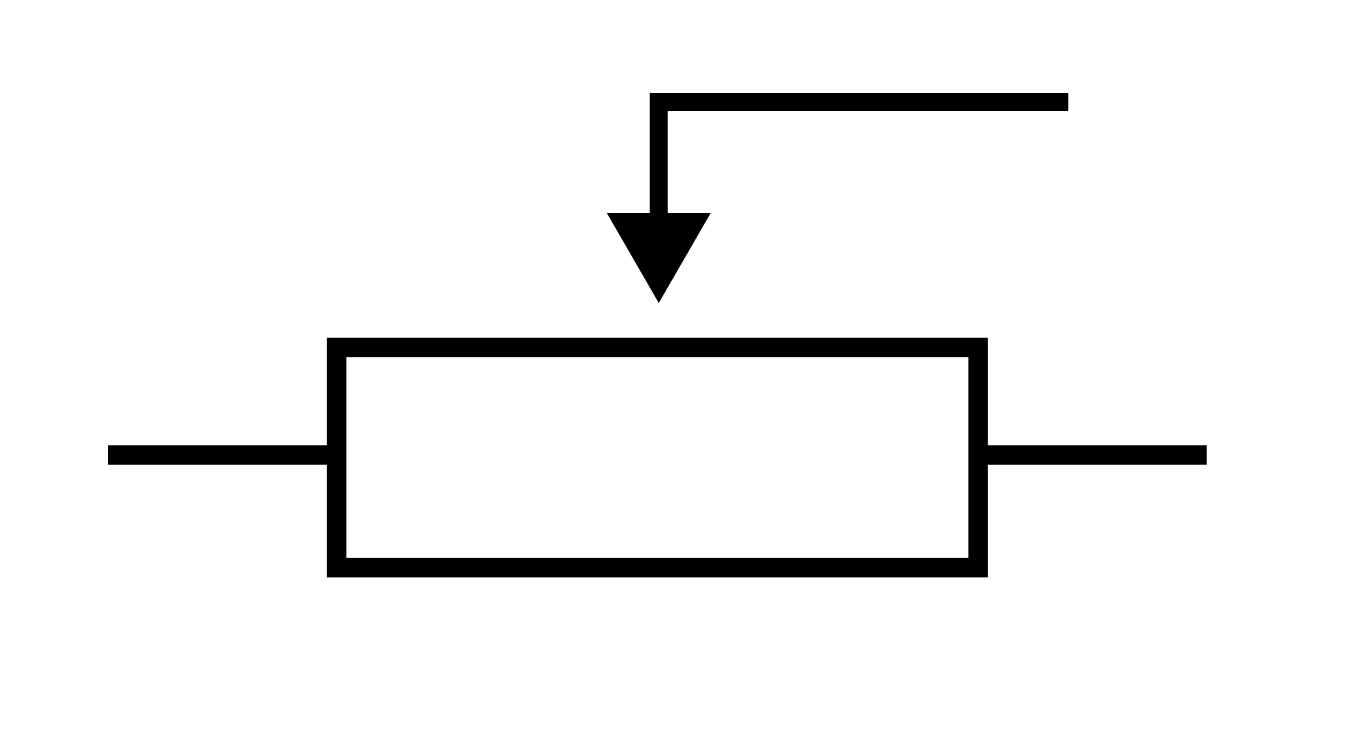
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.

Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.

По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:

Сопротивление

R = ρ l/S

R — сопротивление [Ом]

l — длина проводника [м]

S — площадь поперечного сечения [мм^2]

ρ — удельное сопротивление [Ом*мм^2/м]

Закон Ома для участка цепи

С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.

Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. Эти реакции выделяют энергию, которая потом передается электрической цепи.

У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «-».

У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.

Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.

Математически его можно описать вот так:

Закон Ома для участка цепи

I = U/R

R — сопротивление [Ом]

Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.

Сила тока измеряется в Амперах, а подробнее о ней вы можете прочитать в нашей статье 😇

Давайте решим несколько задач на Закон Ома для участка цепи.

Задача раз

Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.

Решение:

Возьмем закон Ома для участка цепи:

Ответ: сила тока, проходящего через лампочку, равна 0,25 А

Давайте усложним задачу. И найдем силу тока, знаю все параметры для вычисления сопротивления и напряжение.

Задача два

Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм^2, а удельное сопротивление нити равно 1,05 Ом*мм^2/м.

Решение:

Сначала найдем сопротивление проводника.

Площадь дана в мм^2, а удельное сопротивления тоже содержит мм^2 в размерности.

Это значит, что можно подставлять значения без перевода в СИ:

R = 1,05*0,5/0,01 = 52,5 Ом

Теперь возьмем закон Ома для участка цепи:

Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А

А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.

Задача три

Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм^2, а сила тока в цепи — 8,8 А

Решение:

Возьмем закон Ома для участка цепи и выразим из него сопротивление:

Подставим значения и найдем сопротивление нити:

Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:

Подставим значения и получим:

ρ = 25*0,01/0,5 = 0,5 Ом*мм^2/м

Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.

Таблица удельных сопротивлений различных материалов

Константан ( сплав Ni-Cu + Mn)

Нейзильбер (сплав меди цинка и никеля)

Никелин ( сплав меди и никеля)

Нихром ( сплав никеля хрома железы и марганца)

Ответ: нить накаливания сделана из константана.

Закон Ома для полной цепи

Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.

В таком случае вводится Закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.

Так, стоп. Слишком много незнакомых слов — разбираемся по-порядку.

Что такое ЭДС и откуда она берется

ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.

Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь. Именно эта энергия заставляет частицы двигаться по проводнику.

Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.

В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:

Закон Ома для полной цепи

I = ε/(R + r)

R — сопротивление [Ом]

r — внутреннее сопротивление источника [Ом]

Любой источник не идеален. В задачах это возможно («источник считать идеальным», вот эти вот фразочки), но в реальной жизни — точно нет. В связи с этим у источника есть внутреннее сопротивление, которое мешает протеканию тока.

Решим задачу на полную цепь.

Задачка

Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом

Решение:

Возьмем закон Ома для полной цепи:

Ответ: сила тока в цепи равна 1 А.

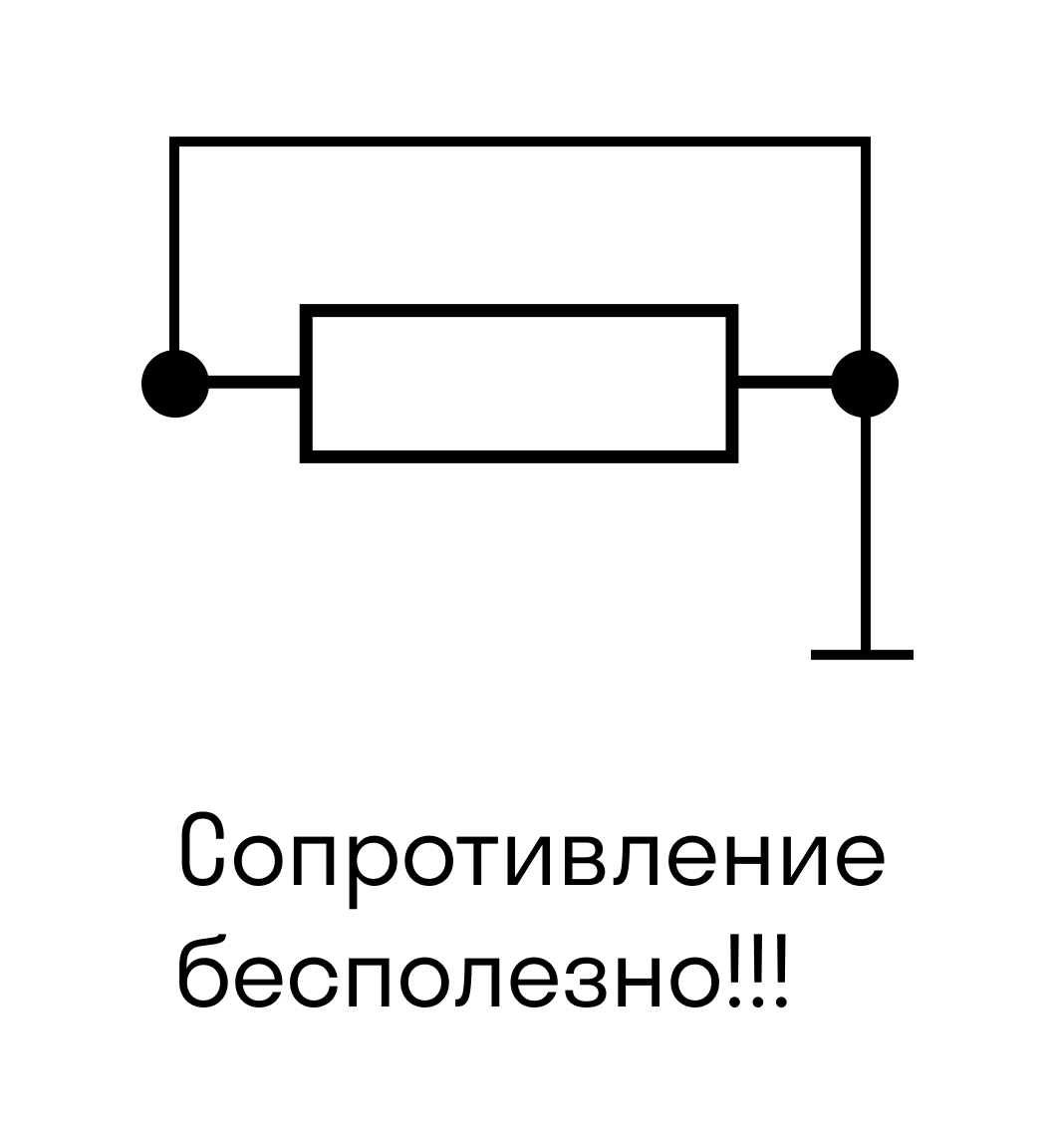
Когда «сопротивление бесполезно»

Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает. При этом с резисторами просто разных номиналов это не сработает: он не пойдет просто через меньшее сопротивление, а распределится согласно закону Ома — больше тока пойдет туда, где сопротивление меньше, и наоборот.

А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.

Ток идет по пути наименьшего сопротивления.

Теперь давайте посмотрим на закон Ома для участка цепи еще раз.

Закон Ома для участка цепи

I = U/R

R — сопротивление [Ом]

Подставим сопротивление, равное 0. Получается, что знаменатель равен нулю, а на математике говорят, что на ноль делить нельзя. Но мы вам раскроем страшную тайну, только не говорите математикам: на ноль делить можно. Если совсем упрощать такое сложное вычисление (а именно потому что оно сложное, мы всегда говорим, что его нельзя производить), то получится бесконечность.

Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.

Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.

Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.

Параллельное и последовательное соединение

Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.

Резисторы следуют друг за другом

Между резисторами есть два узла

Узел — это соединение трех и более проводников

Сила тока одинакова на всех резисторах

Сила тока, входящего в узел, равна сумме сил токов, выходящих из него

Общее напряжение цепи складывается из напряжений на каждом резисторе

Напряжение одинаково на всех резисторах

Общее сопротивление цепи складывается из сопротивлений каждого резистора

Общее сопротивление для бесконечного количества параллельно соединенных резисторов

1/R = 1/R1 + 1/R2 + … + 1/Rn

Общее сопротивление для двух параллельно соединенных резисторов

Общее сопротивление бесконечного количества параллельно соединенных одинаковых резисторов

Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала?

Начнем с того, что все электронные компоненты изготавливаются по ГОСТу. То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов.

Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой.

Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного.

Решим несколько задач на последовательное и параллельное соединение.

Задачка раз

Найти общее сопротивление цепи.

R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.

Решение:

Общее сопротивление при последовательном соединении рассчитывается по формуле:

R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом

Ответ: общее сопротивление цепи равно 10 Ом

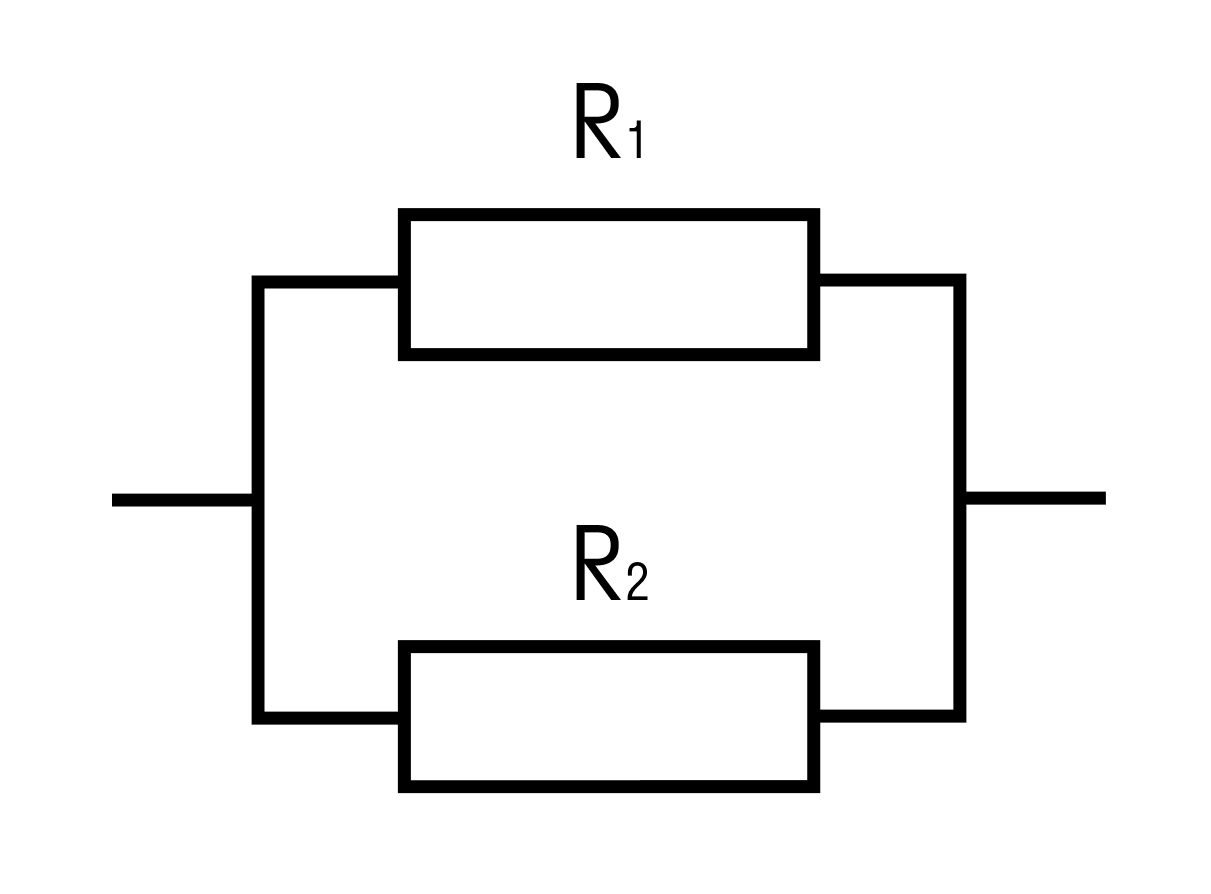
Задачка два

Найти общее сопротивление цепи.

Решение:

Общее сопротивление при параллельном соединении рассчитывается по формуле:

R = (R1 * R2)/R1 + R2 = 4*2/4+2 = 4/3 = 1 ⅓ Ом

Ответ: общее сопротивление цепи равно 1 ⅓ Ом

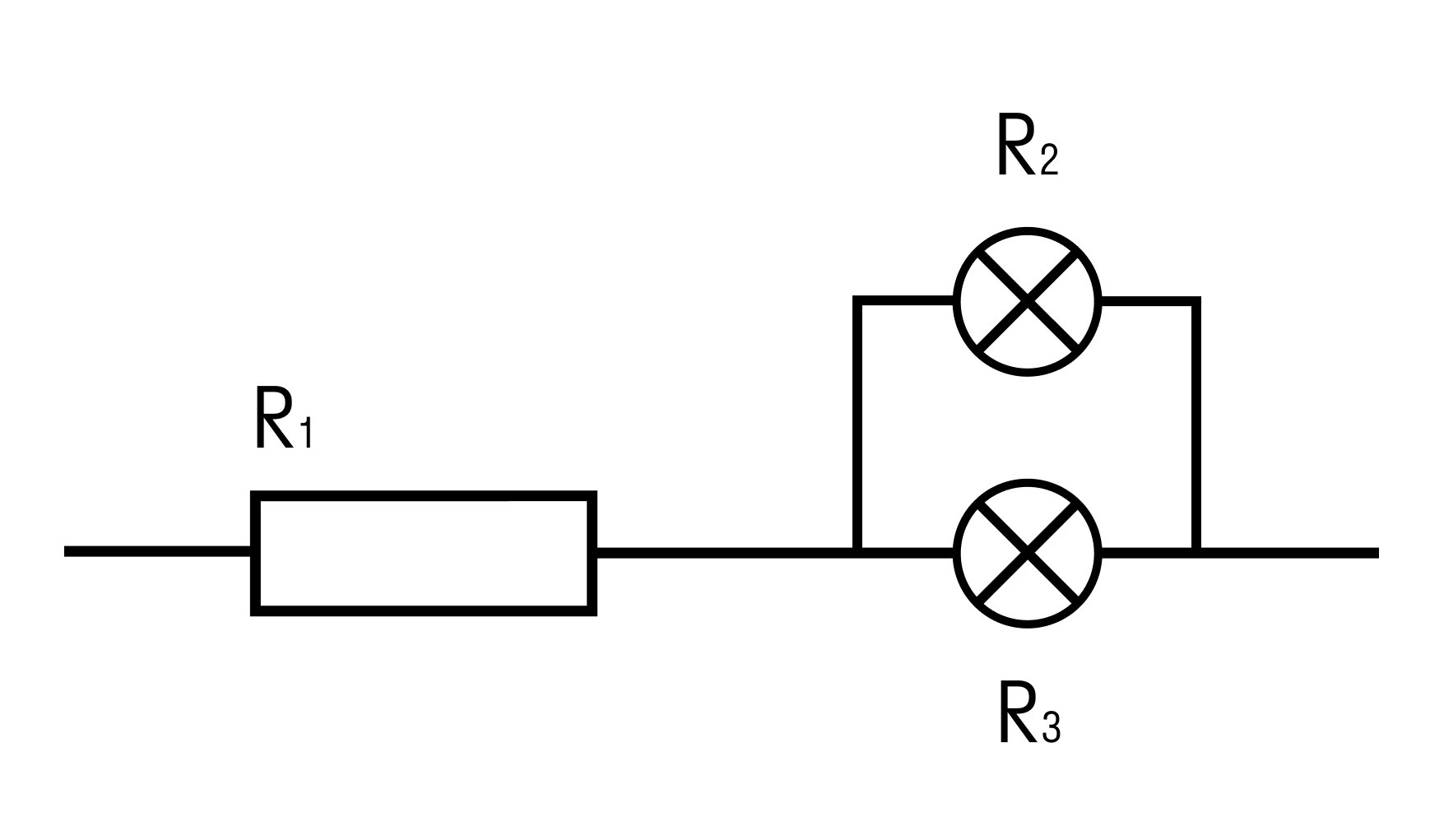
Задачка три

Найти общее сопротивление цепи, состоящей из резистора и двух ламп.

R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом

Решение:

Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.

В данном случае соединение является смешанным. Лампы соеденены параллельно, а последовательно к ним подключен резистор.

Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:

Rламп = (R2 * R3)/R2 + R3 = 2*3/2+3 = 6/5 = 1,2 Ом

Общее сопротивление при последовательном соединении рассчитывается по формуле:

R = R1 + Rламп = 1 + 1,2 = 2,2 Ом

Ответ: общее сопротивление цепи равно 2,2 Ом.

Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи 💪.

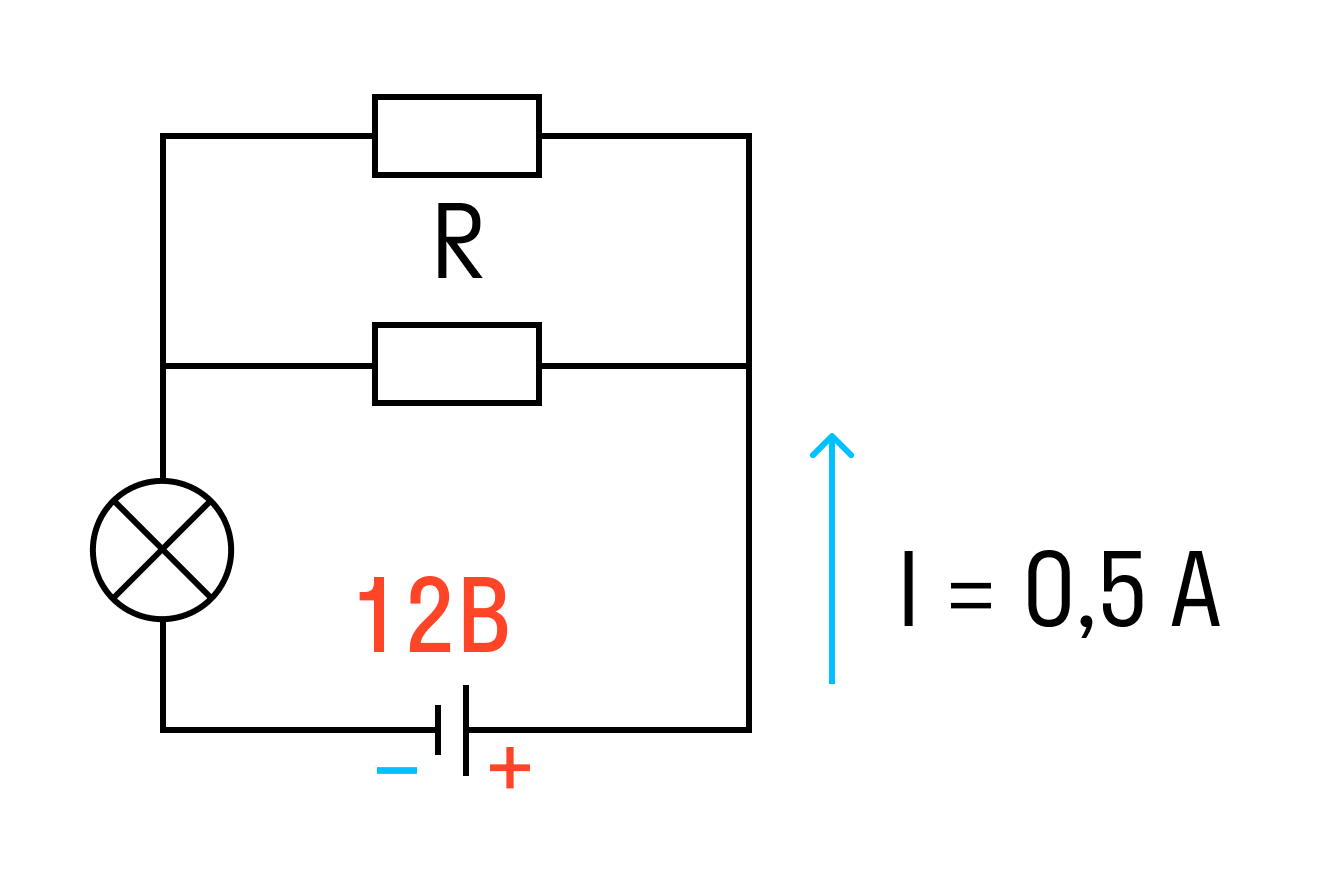
Задачка четыре со звездочкой

К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.

Решение:

Найдем сначала сопротивление лампы.

Rлампы = R/2 = 10/2 = 5 Ом

Теперь найдем общее сопротивление двух параллельно соединенных резисторов.

Rрезисторов = (R * R)/R + R = R^2)/2R = R/2 = 10/2 = 5 Ом

И общее сопротивление цепи равно:

R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом

Выразим внутреннее сопротивление источника из закона Ома для полной цепи.

r = 12/0,5 — 10 = 14 Ом

Ответ: внутреннее сопротивление источника равно 14 Ом.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник