Уравнение аррениуса предэкспоненциальный множитель чему равен
Уравнение аррениуса предэкспоненциальный множитель чему равен
ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов биофака ЮФУ (РГУ)
2.1 СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ
2.1.9 Влияние температуры на константу скорости реакции
Константа скорости реакции есть функция от температуры; повышение температуры, как правило, увеличивает константу скорости. Первая попытка учесть влияние температуры была сделана Я. Г. Вант-Гоффом, который сформулировал следующее эмпирическое правило:
При повышении температуры на каждые 10 градусов константа скорости элементарной химической реакции увеличивается в 2 – 4 раза.
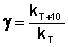
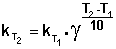
Однако правило Вант-Гоффа применимо лишь в узком температурном интервале, поскольку температурный коэффициент скорости реакции γ сам является функцией от температуры; при очень высоких и очень низких температурах γ становится равным единице (т.е. скорость химической реакции перестает зависеть от температуры).
2.1.10 Уравнение Аррениуса
Очевидно, что взаимодействие частиц осуществляется при их столкновениях; однако число столкновений молекул очень велико и, если бы каждое столкновение приводило к химическому взаимодействию частиц, все реакции протекали бы практически мгновенно. С. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации.
Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию.
Рассмотрим путь некоторой элементарной реакции
Поскольку химическое взаимодействие частиц связано с разрывом старых химических связей и образованием новых, считается, что всякая элементарная реакция проходит через образование некоторого неустойчивого промежуточного соединения, называемого активированным комплексом:
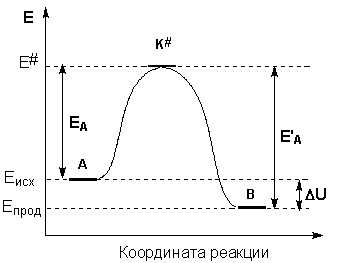
Образование активированного комплекса всегда требует затраты некоторого количества энергии, что вызвано, во-первых, отталкиванием электронных оболочек и атомных ядер при сближении частиц и, во-вторых, необходимостью построения определенной пространственной конфигурации атомов в активированном комплексе и перераспределения электронной плотности. Таким образом, по пути из начального состояния в конечное система должна преодолеть своего рода энергетический барьер. Энергия активации реакции приближённо равна превышению средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что если прямая реакция является экзотермической, то энергия активации обратной реакции Е’А выше, нежели энергия активации прямой реакции EA. Энергии активации прямой и обратной реакции связаны друг с другом через изменение внутренней энергии в ходе реакции. Вышесказанное можно проиллюстрировать с помощью энергетической диаграммы химической реакции (рис. 2.5).
Рис. 2.5 Энергетическая диаграмма химической реакции.
Eисх – средняя энергия частиц исходных веществ,
Eпрод – средняя энергия частиц продуктов реакции
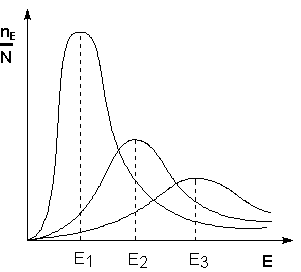
Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6):
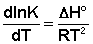
Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (II.31) следующим образом:
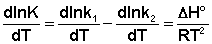
Представив изменение энтальпии реакции ΔHº в виде разности двух величин E1 и E2, получаем:
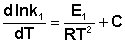
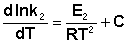
Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где EA – энергия активации :
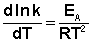
После неопределенного интегрирования выражения (II.35) получим уравнение Аррениуса в интегральной форме:
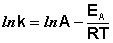
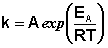
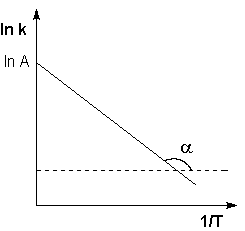
Рис. 2.7 Зависимость логарифма константы скорости химической
реакции от обратной температуры.
Здесь A – постоянная интегрирования. Из уравнения (II.37) нетрудно показать физический смысл предэкспоненциального множителя A, который равен константе скорости реакции при температуре, стремящейся к бесконечности. Как видно из выражения (II.36), логарифм константы скорости линейно зависит от обратной температуры (рис.2.7); величину энергии активации EA и логарифм предэкспоненциального множителя A можно определить графически (тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат).
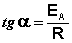
Зная энергию активации реакции и константу скорости при какой-либо температуре T1, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T2:
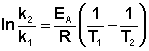
Уравнение аррениуса предэкспоненциальный множитель чему равен
По Аррениусу константа скорости и энергия активации связаны соотношением, получившим название уравнения Аррениуса:
| (5.3) |
Здесь – предэкспоненциальный множитель, – универсальная газовая постоянная, – абсолютная температура.
На рис. 5.4 видно, что затрачиваемая на перевод начальных продуктов в активное состояние (А* – активированный комплекс) энергия затем полностью или частично вновь выделяется при переходе к конечным продуктам. Разность энергий начальных и конечных продуктов определяет реакции, которая от энергии активации не зависит.
Стерический фактор учитывает то обстоятельство, что для взаимодействия сложных активных молекул необходима определенная взаимная ориентация: течению процессов способствует столкновение молекул в положениях, когда в соприкосновение приходят их реакционноспособные связи или неподеленные пары электронов.
Таким образом, уравнение Аррениуса имеет вид
|
Здесь – число всех соударений, – доля соударений, благоприятных в пространственном отношении (принимает значения от 0 до 

Размерность константы скорости получается из соотношения
 |
и, как видно из уравнения Аррениуса, размерность предэкспоненты та же.
| 10 13 –10 14 c –1 | 10 11 –10 12 л∙моль –1 c –1 | 10 9 –10 11 л∙моль –1 c –1 |
Анализируя выражение (5.3), приходим к выводу, что существуют две принципиальные возможности ускорения реакции:
а) увеличение температуры,
б) снижение энергии активации.
Уравнение Аррениуса. Предэкспоненциальный множитель. Стерический фактор.



При фиксированной температуре Т реакция возможна, если взаимодействующие молекулы обладают определенным запасом энергии. Эту избыточную энергию Аррениус назвал энергией активации, а сами молекулы активированными. Аррениус вывел уравнение, связывающее константу скорости с энергией активации и температурой
К=А 
е-экспонент
Еа – энергия активации
R – газовая постоянная
Величина Еа характеризует природу реагирующего вещества и определяется экспериментально из зависимости константы скорости при разных температурах. K=f(T)
Если записать уравнение Аррениуса в логарифмическом виде и рашать его для констант при двух температурах, то можно легко определить
предэкспоненциальный множитель –характеризует общее число соударений для реакции с простыми молекулами. Этот множитель близок к теоретической величине соударений(z)
z рассчитывается из кинетической теории газов А = z
Для сложных молекул А≠ z,поэтому вводится стерический фактор А = zp
Cтерический фактор учитывает то обстоятельство, что для взаимодействия сложных активных молекул необходима определенная взаимная ориентация: течению процессов способствует столкновение молекул в положениях когда в соприкосновениях приходят их реакционно-способные связи или неподеленые пары электронов
z-число всех соударений
p-доля соударений благоприятных в пространственном отношении
e–Ea/RT доля благоприятных в энергетическом отношении соударений
Анализируя уравнение Аррениуса делаем вывод, что существуют две принципиальные возможности ускорения реакции: 1)увеличение температуры 2)снижение энергии активации.
Калькулятор уравнения Аррениуса
(Единицы для постоянной Аррениуса и константы скорости одинаковы и зависят от скорости реакции. )
Что такое уравнение Аррениуса?
Уравнение Аррениуса — это формула, которая описывает, как скорость реакции изменяется в зависимости от температуры или константы скорости. Если мы посмотрим на уравнение, которое использует этот калькулятор уравнения Аррениуса, мы можем попытаться понять, как оно работает:
k = константа скорости, с единицами, которые зависят от порядка реакции, n, в общем виде M1-n * s-1;
A = предэкспоненциальный фактор, иногда называемый константой Аррениуса, в тех же единицах, что и константа скорости;
e ≈ 2,72 = число Эйлера (показатель степени);
Ea = энергия активации реакции, Дж * моль-1;
R = универсальная газовая постоянная, равная 8,314 Дж * К-1 * моль-1; а также
T = температура, в К.
Указанный выше n — это порядок рассматриваемой реакции.
Что означает энергия активации Eₐ?
Теперь, как уравнение Аррениуса работает для определения константы скорости? Что ж, мы начнем с R * T. Умножая эти два значения вместе, мы получаем энергию молекул в системе в Дж * моль-1 при температуре T.
Затем мы можем разделить Ea на это число, что дает нам безразмерное число, представляющее количество столкновений, которые происходят с достаточной энергией, чтобы преодолеть требования к энергии активации (если мы не принимаем во внимание ориентацию). Это число обратно пропорционально количеству успешных столкновений. Таким образом, чем он ниже, тем больше удачных столкновений. Например, для заданного времени t значение Ea / (R * T) = 0,5 означает, что происходит вдвое больше успешных столкновений, чем если бы Ea / (R * T) = 1, что, в свою очередь, имеет вдвое больше количество успешных коллизий, чем Ea / (R * T) = 2.
Что такое уравнение Аррениуса — e, A и k?
Уравнение Аррениуса kB
Возможно, вы заметили, что приведенное выше объяснение уравнения Аррениуса касается вещества на основе на моль, но что, если вы хотите найти одну из переменных на основе расчета на молекулу? Что ж, в этом случае изменение довольно простое; вы замените универсальную газовую постоянную R на постоянную Больцмана kB и сделайте единицы энергии активации J * молекула-1:
k = константа скорости, с единицами, которые зависят от порядка реакции, n, в общем виде M1-n * s-1;
A = предэкспоненциальный фактор, иногда называемый константой Аррениуса, в тех же единицах, что и константа скорости;
e ≈ 2,72 = число Эйлера (показатель степени);
Ea = энергия активации реакции, Дж * молекула-1;
kB = постоянная Больцмана, равная 1,380649 × 10−23 Дж * K-1; а также
T = температура, в К.
Калькулятор уравнения Аррениуса также позволяет выполнять вычисления с использованием этой формы, выбирая параметр для каждой молекулы в самом верхнем поле.
Уравнение Аррениуса ln и график уравнения Аррениуса
Что замечательно в уравнении Аррениуса, так это то, что, решив его однажды, вы можете найти константу скорости реакции при любой температуре. Сложность в том, что экспоненциальная функция — не очень приятная графическая форма для работы. Итак, если вам нужен график уравнения Аррениуса, вы, скорее всего, будете использовать форму ln уравнения Аррениуса:
Это имеет поразительное сходство с уравнением для прямой линии y = mx + c, где
Вот пример уравнения Аррениуса.
2NO2 (г) → 2NO (г) + O2 (г)
При 320 ° C NO2 разлагается с константой скорости 0,5 М * с-1. Экспериментально установлено, что энергия активации этой реакции составляет 115 кДж * моль-1. Что такое предэкспоненциальный множитель?
Первым делом вам нужно преобразовать единицы, чтобы вы могли использовать их в уравнении Аррениуса.
преобразование температуры: 320 ° C + 273,15 = 593,15 K; а также
преобразование энергии: 115 кДж * моль-1 * 1000 = 115000 Дж * моль-1.
Теперь, когда вы это сделали, вам нужно изменить уравнение Аррениуса, чтобы найти A.
Глава II. Энергия активации и предэкспоненциальный множитель
Химический факультет
КАФЕДРА Физической химий и химической экологии
КУРСОВАЯ РАБОТА ПО ДИСЦИПЛИНЕ
Уравнение Аррениуса. Вычисление энергии активации и предэкспоненциального множителя из экспериментальных данных
| Выполнил: Студент(ка) 4 курса очной формы обучения Направление подготовки 04.03.01 Химия Профиль ВМС_________________________ |
| Тимофеева Дарья Витальевна Проверил: к.х.н., доцент Насретдинова Р.Н. _________________ (подпись) «___»____________20____г. |
Содержание
Глава I.Уравнение Аррениуса 4
Глава II. Глава II. Энергия активации и предэкспоненциальный множитель 7
Глава III. Экспериментальное вычисление параметров уравнения 19
Список использованной литературы 11
Введение
Работа разделена на три части. В первой опора сделана на уравнение Аррениуса. Показан его вывод, а именно, переход от изобары Вант-Гоффа.
Во второй на энергию активации и на предэкспонециальный множитель. Их неразрывную связь.
Некоторые ученые считают, что все методы оценки константы скорости реакции хороши, но наиболее обоснованно выражает температурную зависимость уравнение Аррениуса. Приведено экспериментальное описание кинетических процессов с помощью аналитических и графических расчетов.
Актуальность выбранной темы такова, что без определения энергии активации реакции невозможно запустить процессы, потенциально реализуемые в системе. Степень изученности темы определяется исследованиями различных технических институтов в сотрудничестве физико-химическими объединениями.
Цель работы в том, чтобы кратко и точно охарактеризовать каждую шаг вычисления. А задачами являются разбиение комплексной темы на элементарные области. В конце работы дана литература для уточнения информации. Помимо основных источников есть и дополнительные, знакомство с которыми должно способствовать многофункциональному пониманию темы. Каждому хорошему химику нужно уметь пользоваться справочниками, оперировать параметрами, чтобы в заключении свести все теоретические выводы к единому и практическому целому.
В 1889 г. шведский ученый Сванте Аррениус на основании экспериментов вывел уравнение, которое названо его именем:

где k – константа скорости реакции; А – предэкспоненциальный множитель; е – основание натурального логарифма; Еа – постоянная, называемая энергией активации, определяемая природой реакции. Значения Еа для химических реакций лежат в пределах 40 – 400 кДж/ моль.

| (рис 1) |
Если представить графическую зависимость lnk = f(1/T), то она имеет вид (рис 1).
Итак, константа скорости реакции (и скорость) возрастает с увеличением температуры по экспоненциальному закону. В соответствии с уравнением Аррениуса константа скорости реакции уменьшается с ростом энергии активации. Уравнение Аррениуса позволяет рассчитывать константы скорости (и скорости) при различных температурах.
Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6):

Энергия, необходимая для перехода вещества в состояние активированного комплекса, называется энергией активации.
Образование активированного комплекса определяется энергией молекул. Молекула, энергия которой достаточна для образования активированного комплекса, называется активной. Доля таких молекул зависит от температуры. При высоких температурах доля активных молекул, энергия которых равна или выше энергии активации, велика и, соответственно, растет доля молекул 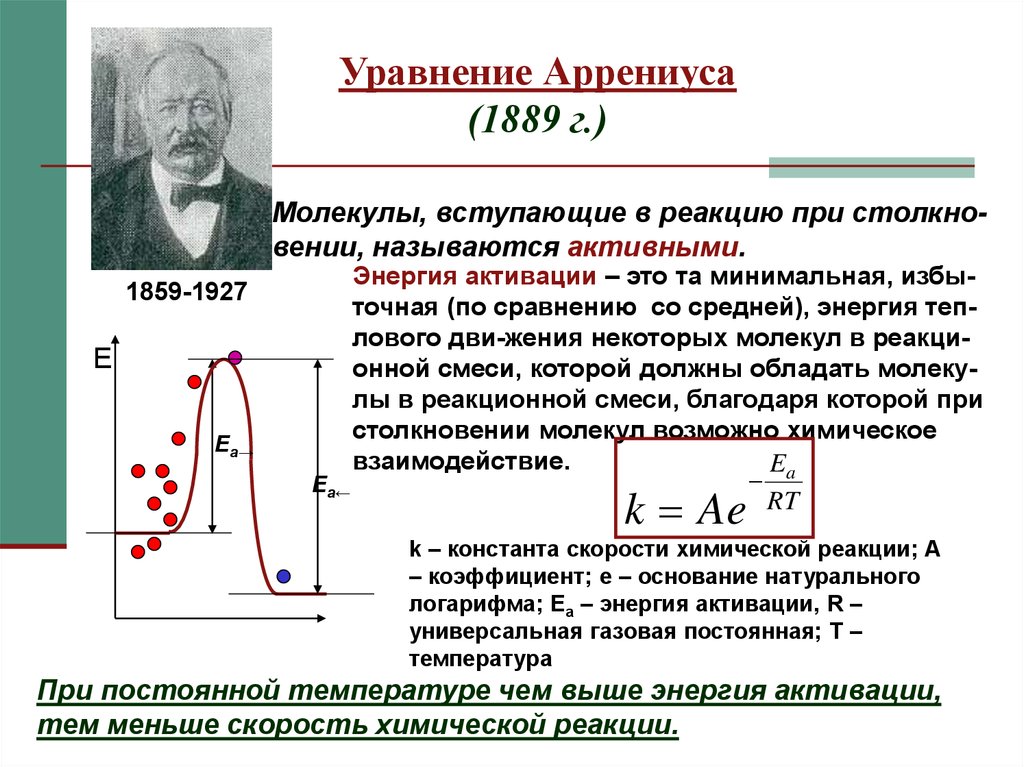
Дата добавления: 2019-02-26 ; просмотров: 1240 ; Мы поможем в написании вашей работы!






Warning: Use of undefined constant expert_review_likes - assumed 'expert_review_likes' (this will throw an Error in a future version of PHP) in /var/www/www-ars1963/data/www/ck62.ru/wp-content/themes/colormag/comments.php on line 93