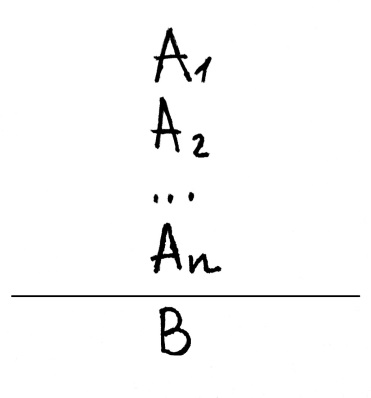Умозаключение и вывод в чем разница

Сделаем вывод (Что такое умозаключение)

Умозаключение – это форма мышления, в которой из двух или нескольких суждений, называемых посылками, вытекает новое суждение, называемое заключением (выводом). Например:

Все живые организмы питаются влагой.

Все растения – это живые организмы.

=> Все растения питаются влагой.

В приведенном примере первые два суждения являются посылками, а третье – выводом. Посылки должны быть истинными суждениями и должны быть связаны между собой. Если хотя бы одна из посылок ложна, то и вывод ложен:

Все птицы – это млекопитающие животные.

Все воробьи – это птицы.

=> Все воробьи – это млекопитающие животные.

Как видим, в приведенном примере ложность первой посылки приводит к ложному выводу, несмотря на то что вторая посылка является истинной. Если посылки между собой не связаны, то вывод из них сделать невозможно. Например, из следующих двух посылок никакого вывода не следует:

Все планеты – это небесные тела.

Все сосны являются деревьями.

Обратим внимание на то, что умозаключения состоят из суждений, а суждения – из понятий, т. е. одна форма мышления входит в другую в качестве составной части.

Все умозаключения делятся на непосредственные и опосредованные.

В непосредственных умозаключениях вывод делается из одной посылки. Например:

Все цветы являются растениями.

=> Некоторые растения являются цветами.

Верно, что все цветы являются растениями.

=> Неверно, что некоторые цветы не являются растениями.

Нетрудно догадаться, что непосредственные умозаключения представляют собой уже известные нам операции преобразования простых суждений и выводы об истинности простых суждений по логическому квадрату. Первый приведенный пример непосредственного умозаключения является преобразованием простого суждения путем обращения, а во втором примере по логическому квадрату из истинности суждения вида А делается вывод о ложности суждения вида О.

В опосредованных умозаключениях вывод делается из нескольких посылок. Например:

Все рыбы – это живые существа.

Все караси – это рыбы.

=> Все караси – это живые существа.

Опосредованные умозаключения делятся на три вида: дедуктивные, индуктивные и умозаключения по аналогии.

Дедуктивные умозаключения (дедукция) (от лат. deductio – «выведение») – это умозаключения, в которых из общего правила делается вывод для частного случая (из общего правила выводится частный случай). Например:

Все звезды излучают энергию.

Солнце – это звезда.

=> Солнце излучает энергию.

Как видим, первая посылка представляет собой общее правило, из которого (при помощи второй посылки) вытекает частный случай в виде вывода: если все звезды излучают энергию, значит, Солнце тоже ее излучает, потому что оно является звездой.

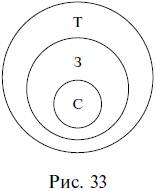
В дедукции рассуждение идет от общего к частному, от большего к меньшему, знание сужается, в силу чего дедуктивные выводы достоверны, т. е. точны, обязательны, необходимы. Посмотрим еще раз на приведенный пример. Мог бы из двух данных посылок вытекать иной вывод, кроме того, который из них вытекает? Не мог. Вытекающий вывод – единственно возможный в этом случае. Изобразим отношения между понятиями, из которых состояло наше умозаключение, кругами Эйлера. Объемы трех понятий: звезды (3); тела, излучающие энергию (Т) и Солнце (С) схематично расположатся следующим образом (рис. 33).

Если объем понятия звезды включается в объем понятия тела, излучающие энергию, а объем понятия Солнце включается в объем понятия звезды, то объем понятия Солнце автоматически включается в объем понятия тела, излучающие энергию, в силу чего дедуктивный вывод и является достоверным.

Несомненное достоинство дедукции заключается в достоверности ее выводов. Вспомним, известный литературный герой Шерлок Холмс пользовался дедуктивным методом при раскрытии преступлений. Это значит, что он строил свои рассуждения таким образом, чтобы из общего выводить частное. В одном произведении, объясняя доктору Ватсону сущность своего дедуктивного метода, он приводит такой пример. Около убитого полковника Эшби сыщики Скотланд-Ярда обнаружили выкуренную сигару и решили, что полковник выкурил ее перед смертью. Однако Шерлок Холмс неопровержимо доказывает, что полковник не мог выкурить эту сигару, потому что он носил большие, пышные усы, а сигара выкурена до конца, т. е., если бы ее курил полковник Эшби, то он непременно подпалил бы свои усы. Следовательно, сигару выкурил другой человек.

В этом рассуждении вывод выглядит убедительно именно потому, что он дедуктивный – из общего правила: Любой человек с большими, пышными усами не может выкурить сигару до конца, выводится частный случай: Полковник Эшби не мог выкурить сигару до конца, потому что носил такие усы. Приведем рассмотренное рассуждение к принятой в логике стандартной форме записи умозаключений в виде посылок и вывода:

Любой человек с большими, пышными усами не может выкурить сигару до конца.

Полковник Эшби носил большие, пышные усы.

=> Полковник Эшби не мог выкурить сигару до конца.

Индуктивные умозаключения (индукция) (от лат. inductio – «наведение») – это умозаключения, в которых из нескольких частных случаев выводится общее правило. Например:

Юпитер, Марс, Венера – это планеты.

=> Все планеты движутся.

Первые три посылки представляют собой частные случаи, четвертая посылка подводит их под один класс объектов, объединяет их, а в выводе говорится обо всех объектах этого класса, т. е. формулируется некое общее правило (вытекающее из трех частных случаев).

Легко увидеть, что индуктивные умозаключения строятся по принципу, противоположному построению дедуктивных умозаключений. В индукции рассуждение идет от частного к общему, от меньшего к большему, знание расширяется, в силу чего индуктивные выводы (в отличие от дедуктивных) не достоверны, а вероятностны. В рассмотренном выше примере индукции признак, обнаруженный у некоторых объектов какой-то группы, перенесен на все объекты этой группы, сделано обобщение, которое почти всегда чревато ошибкой: вполне возможно наличие в группе каких-то исключений, и даже если множество объектов из некоторой группы характеризуется каким-то признаком, то это не означает, что таким признаком характеризуются все объекты данной группы. Вероятностный характер выводов является, конечно же, недостатком индукции. Однако ее несомненное достоинство и выгодное отличие от дедукции, которая представляет собой сужающееся знание, заключается в том, что индукция – это расширяющееся знание, способное приводить к новому, в то время как дедукция – это разбор старого и уже известного.

Умозаключения по аналогии (аналогия) (от греч. analogia – «соответствие») – это умозаключения, в которых на основе сходства предметов (объектов) в одних признаках делается вывод об их сходстве и в других признаках. Например:

Планета Земля расположена в Солнечной системе, на ней есть атмосфера, вода и жизнь.

Планета Марс расположена в Солнечной системе, на ней есть атмосфера и вода.

=> Вероятно, на Марсе есть жизнь.

Как видим, сопоставляются два объекта (планета Земля и планета Марс), которые сходны между собой в некоторых существенных, важных признаках (находиться в Солнечной системе, иметь атмосферу и воду). На основе данного сходства делается вывод о том, что, возможно, эти объекты сходны между собой и в других признаках: если на Земле есть жизнь, а Марс во многом похож на Землю, то не исключено наличие жизни и на Марсе. Выводы аналогии, как и выводы индукции, вероятностны.

Источник

10. Краткий курс логики. Умозаключение

Умозаключение – это форма мышления, в которой из двух суждений, называемых посылками, вытекает третье – вывод.
1. Посылка: «Все люди – смертны».
2. Посылка: «Сократ – человек»
Ввод: «Сократ – смертный».

Умозаключения бывают непосредственные и опосредованные. Непосредственные умозаключения делаются из одной посылки, и являют собой уже известные нам действия над суждениями (обращения, превращения, противоставления предикату), а так же преобразование суждений по логическому квадрату. Опосредованные умозаключения делаются из нескольких посылок, о них мы и будем говорить в данной главе.

Существуют такие виды опосредованных умозаключений, их еще называют методами мышления:

Дедуктивный метод (Силлогизм) – метод при котором вывод о частном делается из общей совокупности вещей, о которых говориться в посылках. Проще говоря – вывод от общего к частному. К примеру:
1 посылка: «В группе 311 все студенты отличники».
2 посылка: «Этот ученик из 311 группы»
Вывод: «Этот ученик – отличник».
Еще пример:
1 посылка: «В этом ящике все шарики красные»
2 посылка: «Этот шарик их этого ящика»
Вывод: «Этот шарик красный».

Преимущество дедуктивного метода заключается в том, что при правильном использовании всегда дает точные выводы. Важно понимать, что все посылки входящие в силлогизм должны быть истинными, ложность хотя бы одной из них, ведет к ложности вывода. В принципе кто знаком с произведениями Артура Конана Дойля, должен был слышать о дедуктивном способе мышления. Его использовал Шерлок Холмс, в одном из произведений он приводит пример своего дедуктивного умозаключения Ватсону. Около жертвы преступления было найдена выкуренная сигарета, все решили, что сигарету выкурил полковник перед смертью. Однако у покойного были большие пышные усы, а сигарета была докуренная полностью. Шерлок Холм берется доказывать, что полковник не мог курить эту сигарету, так как он непременно бы подпалил бы себе усы. Вывод дедуктивный и верный, так как из общего правила вытекает частное.
Общее правило и первая посылка, выглядит так: «Все люди, которые носят большие, пышные усы не могут выкурить сигарету до конца»
Событие или вторая посылка выглядит так: «Полковник носил большие, пышные усы».
Вывод: «Полковник не мог выкурить сигарету до конца»

Индукция – метод, при котором вывод об общем делается из совокупности частных случаев. Проще говоря – это вывод от частного к общему. И пример тому:
1 посылка: «Первый, второй и третий студент – отличники».
2 посылка: «Эти студенты из 311 группы».
Вывод: «Все студенты в 311 группе – отличники».

1 посылка: ««Этот шарик красный».
2 посылка: «Этот шарик их этого ящика».
Вывод: «В этом ящике все шарики красные»

Некоторые учебники различают полную и не полную индукцию, полная индукция это когда перечисляются все элементы конечного множества вещей, о котором рассуждают. В нашем примере берутся все ученики и проверяют отличники они все или нет, а уже потом заключают обо всей группе. Не полная или частичная индукция – это наши примеры, в которых берутся только некоторые элементы конечного множества вещей. Само собой разумеется, не полное индуктивное заключения, на отмену от дедуктивного носит вероятностный, а не достоверный характер. Тем не менее, это не мешает пользоваться этим методом умозаключения в повседневной жизни. К примеру, мы, я уверен, слышали такое высказывание из уст женщины «Все мужчины – козлы», а ведь вывод об общем сделан из частного, по всем правилам индуктивного мышления.
1 посылка: «Первый человек – козел»
2 посылка: «Второй человек – козел».
3 посылка: «Эти люди – мужчины»
Вывод: «Все мужчины – козлы».

Чаще всего не полные индуктивные выводы – неверные. Их преимущество состоит в том, что они направленны на расширения знаний о предмете, могут указать на новые их свойства, в то время как индуктивный метод чаще всего направлен на выяснения уже известных фактов.

Я с некоторыми другими логиками выделяю еще такой вид умозаключения как Абдукция. Абдукция – это вид умозаключения, при котором на основе общего, делается вывод о причине частного, проще говоря – это вывод от общего к причине частного.
Я считаю, на отмену от общепринятого мнения, что именно этот вид умозаключений использовал на самом деле Шерлок Холмс, а так же другие реальные и не реальные детективы.
Чтобы понять, в чем заключается суть Абдукции, ее лучше рассматривать в сравнении с другими видами умозаключения.

А: «В этом ящике все шарики красные»
Б: «Этот шарик их этого ящика»
В: «Этот шарик красный».
Как видим с помощью дедукции – мы узнали результат, теперь переделаем рассуждения под индукцию:

Б: «Этот шарик их этого ящика»
В: «Этот шарик красный».
А: «В этом ящике все шарики красные»
Индукция, вывод от частного к общему открыл нам правило. Не трудно догадаться, что должен быть еще один вид умозаключений, который открывал бы нам случай, причину, ним и является Абдукция. Такой вид умозаключений будет выглядит так:

Существует, еще такой вид умозаключений как «вывод по аналогии». Это когда на основе свойств, признаков одного предмета делается вывод о свойствах другого. Формально это выглядит так:
Предмет А имеет свойство а, б, с, д.
Предмет В имеет свойсво а, б, с.
Вероятно В имеет и свойство д.
Так же как и неполная индукция умозаключения по аналогии носит вероятностный характер, но, не смотря на это, он широко используется, как в повседневной жизни, так и в науке.

Вернемся к дедукции. Мы предположили, что дедуктивный вид умозаключения имеет достоверный характер. Но, тем не менее, надо выделить некоторые правила простого силлогизм, чтобы это было действительно так. Итак, рассмотрим общие правила силлогизма.
1. В силлогизме должно быть только три термина или не должно быть термина, который употребляется в двух значениях. Если такой есть считается, что в силлогизме больше трех терминов, так как четвертый подразумевается. К примеру:
Движение – вечно.
Хождение в университет – это движение.
Хождение в университет – вечно.

Термин «Движение» употреблено в двух смыслах, в первом суждении, первой посылке оно обозначает всеобщее мировое изменения. А во второй механическое передвижение из одной точки в другую.

2. Средний термин должен быть распределён хотя бы в одной из посылок. Средний термин – это термин, который является базисом рассуждения и находиться в каждой из посылок.
Все хищные животные (+) – живые существа (-)
Все хомяки (+) – живые существа (-).
Все хомяки – хищные животные.
Средним термином является «живые существа». В обоих посылках его объем не распределён. В первой посылке оно не распределено, потому, что живые существа – это не только хищные животные. А во втором, потому, что живые существа – это не только все хомяки. Соответственно вывод в данном суждении не верный.
Еще один пример, который недавно прочел в одном журнале:
Все старые фильмы (+) – черно белые (-)
Все пингвины (+) – черно белые (-).
Пингвины – это старые фильмы.
Средний термин, то есть термин, который встречается в двух посылках – «черно белый». Как в первом, так и во втором суждении он не распределён, ведь черно белыми могут быть не только все старые фильмы или все пингвины.

4. Посылки силлогизма не могут быть только отрицательными. Вывод в таком силлогизме в лучшем случае будет вероятностным, но чаще всего его либо вообще невозможно сделать, либо он ложен.

5.Посылки силлогизма не могут быть только частными. Хотя бы одна посылка из силлогизма должна быть общая. В силлогизме, в котором две посылки частные сделать вывод не возможно.

6.Если в силлогизме одна посылка отрицательная, то и вывод будет отрицательным.

7.Если в силлогизме одна посылка частная, вывод из него следует так же только частный.

Силлогизм – самый распространённый вид умозаключений, потому, мы часто используем его в повседневной жизни и науке. Однако мы редко соблюдаем его логическую форму, и пользуемся сокращенными силлогизмами. К примеру: «Сократ смертный, потому, что все люди смертные». «Этот шарик красный, потому, что его взяли из ящика, в котором все шарики красные». «Железо – электропроводно, так как все металлы электропроводны» и т.д.

Различают такие виды сокращенного силлогизма:
Энтимема – это сокращенный силлогизм, в котором пропущена одна из посылок или вывод. Понятно, что из простого силлогизма можно вывести три энтимемы. К примеру, из простого силлогизма:
Все металлы – электропроводные.
Железо – это метал.
Железо – электропроводно.
Можно вывести три энтимемы:
1. «Железо – электропроводно так как оно является металлом». (пропущена первая посылка)
2. «Железо – электропроводно потому, что все металлы электропроводны». (пропущена вторая посылка)
3. «Все металлы электропроводны, а железо тоже метал». (пропущен вывод)

Следующий вид сокращенного умозаключения – Эпихейрема. Оно являет собой простой силлогизм, в которой две посылки – энтимемы.
Сначала сделаем из двух силлогизмов энтимемы:

Силлогизм №1.
Все то, что ограничивает человеческую свободу, делает его рабом.
Социальная необходимость ограничивает человеческую свободу
Социальная необходимость делает человека рабом.

Первая энтимема, если пропустить первую посылку будет выгладить так:
«Социальная необходимость делает человека рабом, потому, что ограничивает человеческую свободу.
Силлогизм №2.
Все действия, которые дают возможность существовать в социуме – являются социальной необходимостью.
Работа – это действие, которое дает возможность существовать в социуме.
Работа – это социальная необходимость.
Вторая энтимема, если пропустить первую посылку: «Работа – это социальная необходимость, так как является действием, которое дает возможность существовать в социуме».

Теперь сделаем силлогизм из двух энтимем, который и будет нашей эпихейремой:
Социальная необходимость делает человека рабом, потому, что ограничивает человеческую свободу.
Работа – это социальная необходимость, так как является действием, которое дает возможность существовать в социуме.
Работа – делает человека рабом.

Не исключено, что именно в таком порядке рассуждал Ницше говоря: «Мы видим, к чему сводится жизнь в обществе — каждый отдельный индивид приносится в жертву и служит орудием. Пройдите по улице, и вы увидите только «рабов». Куда? Зачем?»

Сорит – полисиллогизм, в котором пропущено суждение, связывающее два простых силлогизма, то есть вывод первого силлогизма, который стал первой посылкой второго, попросту упускается.
Все что развивает память и мышления – полезно.
Изучения наук – развивает память и мышления.
Логика – это наука.
Изучения логики – полезно.
Как видим суть силлогизма от того, что оно из полисиллогизма превратилось в сорит, не поменялась.

Источник

Урок 6. Умозаключения

В этом уроке мы, наконец, переходим к теме, которая составляет ядро любого рассуждения и любой логической системы – умозаключениям. В четвёртом уроке мы говорили, что рассуждение – это совокупность суждений или высказываний. Очевидно, что такое определение не полно, ведь оно ничего не говорит о том, почему вдруг какие-то разные высказывания оказались рядом. Если дать более точное определение, то рассуждение – это процесс обоснования какого-либо высказывания с помощью его последовательного вывода из других высказываний. Этот вывод чаще всего осуществляется в форме умозаключений.

Содержание:

Умозаключение – это непосредственный переход от одного или нескольких высказываний А₁, А₂, …, А_n к высказыванию В. А₁, А₂, …, А_n называют посылками. Посылка может быть одна, их может быть две, три, четыре, в принципе – сколько угодно. В посылках содержится известная нам информация. В – это заключение. В заключении находится уже новая информация, которую мы извлекли из посылок с помощью специальных процедур. Эта новая информация уже содержалась в посылках, но в скрытом виде. Так вот задача умозаключения сделать это скрытое явным. Кроме того, иногда посылки называют аргументами, а заключение – тезисом, а само умозаключение в этом случае называют обоснованием. Разница между умозаключением и обоснованием состоит в том, что в первом случае, мы не знаем, к какому заключению мы придём, а во втором – тезис нам уже известен, мы просто хотим установить его связь с посылками-аргументами.

В качестве иллюстрации умозаключения можно взять рассуждения Эркюля Пуаро из «Убийства в восточном экспрессе» Агаты Кристи:

Перебрав в уме еще раз показания пассажиров, я пришел к весьма любопытным результатам. Для начала возьмем показания мистера Маккуина. Первая беседа с ним не вызвала у меня никаких подозрений. Но во время второй он обронил небезынтересную фразу. Я сообщил ему, что мы нашли записку, в которой упоминается о деле Армстронгов. Он сказал: «А разве…» – осекся и, помолчав, добавил: «Ну это самое… неужели старик поступил так опрометчиво?…»

Но я почувствовал, что он перестроился на ходу. Предположим, он хотел сказать: «А разве ее не сожгли?» Следовательно, Маккуин знал и о записке, и о том, что ее сожгли, или, говоря другими словами, он был убийцей или пособником убийцы.

Логики записывают умозаключения следующим образом:

Над чертой располагаются посылки, под чертой – заключение, а сама черта обозначает отношение логического следования.

Критерии истинности умозаключений

Также как и для суждений, для умозаключений существуют определённые условия их истинности. При определении, истинное умозаключение или ложное, нужно обращать внимание на два аспекта. Первый аспект – это истинность посылок. Если хотя бы одна из посылок ложна, то и сделанное заключение тоже будет ложным. Поскольку заключение – это та информация, которая была скрыта в посылках и которую мы просто извлекли на свет, то из неверных посылок невозможно случайно получить верный вывод. Это можно сравнить с попыткой сделать бифштекс из моркови. Наверное, моркови можно придать цвет и форму бифштекса, но внутри всё равно будет морковь, а не мясо. Никакие кулинарные операции не преобразуют одно в другое.

Второй аспект – это правильность самого умозаключения с точки зрения его логической формы. Дело в том, что истинность посылок – это важное, но недостаточное условие для того, чтобы заключение было правильным. Нередки ситуации, когда посылки истинны, но заключение неверно. В качестве примера неправильного умозаключения при истинности посылок можно привести умозаключение голубки из «Алисы в стране чудес» Кэрролла. Голубка обвиняет Алису, в том, что она не змея. Вот как она приходит к этому выводу:

Змеи едят яйца.
Девочки едят яйца.
Значит, девочки – это змеи.

Хотя посылки правильные, заключение абсурдно. Умозаключение в целом сделано неверно. Чтобы избежать подобных ошибок, логики выявили такие умозаключения, логические формы которых при истинности посылок гарантируют истинность заключения. Их принято называть правильными умозаключениями. Таким образом, чтобы умозаключение было сделано верно, нужно следить за истинностью посылок и за правильностью самой формы умозаключения.

Мы рассмотрим различные формы правильных умозаключений на примере силлогистики. В этом уроке мы разберём самые простые однопосылочные заключения. В следующем уроке – более сложные заключения: силлогизмы, энтимемы, многопосылочные заключения.

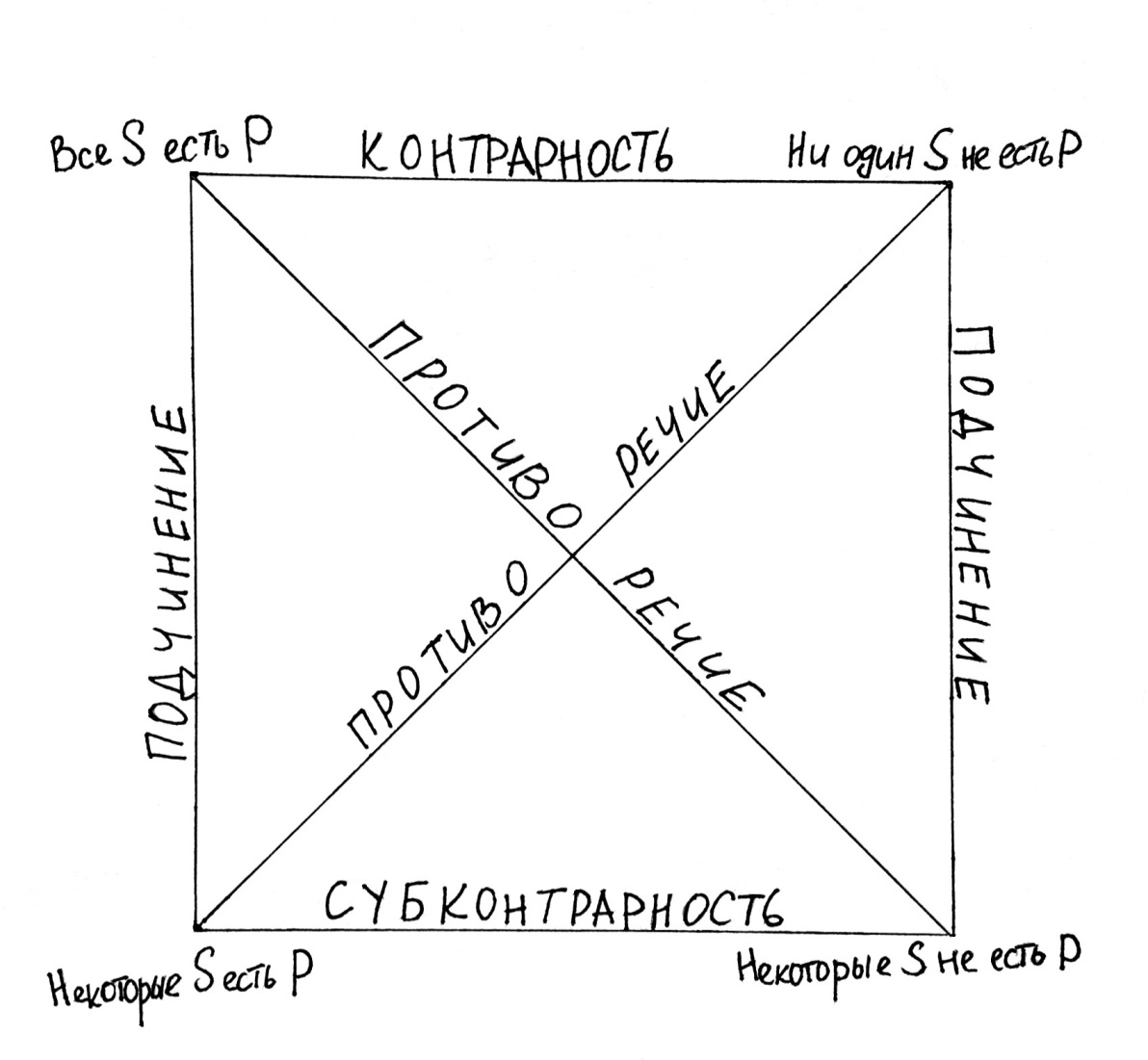
Умозаключения по логическому квадрату

Чтобы было легче запомнить, какие именно типы умозаключений возможны между категорическими атрибутивными высказываниями, логики придумали специальный логический квадрат, изображающий отношения между ними. Поэтому некоторые однопосылочные умозаключения также называют умозаключениями по логическому квадрату. Посмотрим на этот квадрат:

Начнём с отношений подчинения. Мы уже сталкивались с ними в четвёртом уроке, когда рассматривали условия истинности для частно-утвердительных и частно-отрицательных высказываний. Мы говорили, что из высказывания «Все S есть P» будет логичным вывести высказывание «Некоторые S есть P», а из высказывания «Ни один S не есть P» – «Некоторые S не есть P». Таким образом, возможны следующие типы умозаключений:

Кроме того, по правилу контрапозиции из отношений подчинения можно вывести ещё два правильных умозаключения. Правило контрапозиции – это логический закон, который гласит: если из высказывания А следует высказывание В, то из высказывания «неверно, что В» будет следовать высказывание «неверно, что А». Вы можете попробовать проверить этот закон с помощью таблицы истинности. Итак, будут верны и следующие умозаключения по контрапозиции:

Отношение контрарности (противоположности) означает, что высказывания типа «Все S есть P» и «Ни один S не есть P» не могут быть одновременно истинными, но они могут быть одновременно ложными. Это хорошо видно из таблицы истинности для категоричных атрибутивных высказываний, которую мы построили в прошлом уроке. Отсюда можно вывести так называемый закон контрарного противоречия: Неверно, что все S есть P и в то же время ни один S не есть P.

По закону контрарного противоречия будут истинными следующие виды умозаключений:

Отношения субконтрарности (подпротивоположности) означают, что высказывания типа «Некоторые S есть P» и «Некоторые S не есть P» не могут быть одновременно ложными, хотя могут быть одновременно истинными. На этом основании может быть сформулирован закон субконтрарного исключённого третьего: Некоторые S не есть P или Некоторые S есть P.

Отношения противоречия (контрадикторности) говорят о том, что высказывания, находящиеся в них, не могут быть одновременно истинными или ложными. На основании этих отношений можно сформулировать два закона противоречия и два закона исключённого третьего. Первый закон противоречия: Неверно, что все S есть P и некоторые S не есть P. Второй закон противоречия: Неверно, что ни один S не есть P и некоторые S есть P. Первый закон исключённого третьего: Все S есть P или некоторые S не есть P. Второй закон исключённого третьего: Ни один S не есть P или некоторые S есть P.

На этих законах строятся умозаключения следующих видов:

Как вы, скорее всего, заметили во всех этих умозаключениях, высказывания над чертой и под чертой несут одну и ту же информацию, просто поданную в разной форме. Важная деталь заключается в том, что смысл одних из этих высказываний воспринимается легко и интуитивно, в то время как смысл других тёмен, и над ними порой приходится поломать голову. Например, смысл утвердительных высказываний воспринимается легче, чем смысл отрицательных высказываний, смысл высказываний с одним отрицанием более понятен, чем смысл высказываний с двумя отрицаниями. Таким образом, основное назначение умозаключений по логическому квадрату состоит в том, чтобы привести сложные для восприятия, непонятные высказывания к наиболее простой и ясной форме.

Операция обращения

Ещё одним видом однопосылочных умозаключений является обращение. Это такой тип умозаключений, при которых субъект посылки совпадает с предикатом заключения, а субъект заключения совпадает с предикатом посылки. Грубо говоря, в заключении S и P просто меняются местами.

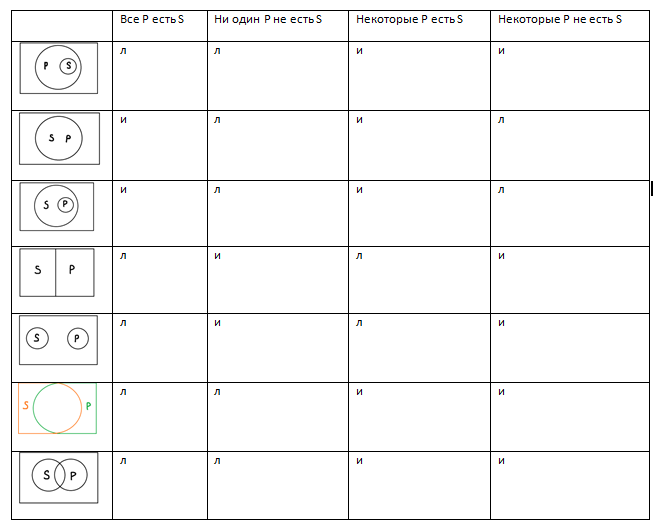
Прежде чем перейти к умозаключениям через обращение, построим таблицу истинности для высказываний, в которых P встанет на место субъекта, а S – на место предиката.

Сравните её с той таблицей, которую мы строили в прошлом уроке. Обращение, как и другие умозаключения, может быть правильным, только когда посылка и заключение одновременно истинны. При сравнении двух таблиц, вы увидите, что таких комбинаций не так уж и много.

Итак, существует два вида обращения: чистое и с ограничением. Чистое обращение происходит тогда, когда количественная характеристика не изменяется, то есть если в посылке было слово «все», то и в заключении тоже будет слова «все»/«ни один», если в посылке слово «некоторые», то и в заключении «некоторые. Соответственно, при обращении с ограничением количественная характеристика меняется: были «все», а стали «некоторые». Для высказываний типа «Ни один S не есть P» и «Некоторые S есть P» правильным будет следующее чистое обращение:

Хотя обращения, как и умозаключения по логическому квадрату, это однопосылочные умозаключения, и мы точно также извлекаем всю новую информацию из имеющейся посылки, посылку и заключение в них уже нельзя назвать просто разными формулировками одной и той же информации. Полученная информация относится уже к другому субъекту, а потому она уже не кажется такой тривиальной.

Итак, в этом уроке мы начали рассматривать правильные виды умозаключений. Мы поговорили о самых простейших однопосылочных умозаключениях: умозаключениях по логическому квадрату и умозаключениях через обращение. Хотя эти умозаключения довольно просты и даже где-то тривиальны, люди повсеместно совершают в них ошибки. Понятно, что сложно удержать в памяти все виды правильных умозаключений, поэтому, когда вы будете выполнять упражнения или столкнётесь с необходимостью проверить или сделать однопосылочное умозаключение в реальной жизни, не бойтесь прибегать к помощи модельных схем и таблиц истинности. Они помогут вам проверить, всегда ли при истинности посылок заключение тоже истинное, а это главное для правильного умозаключения.

Упражнение «Подберите ключ»

В этой игре вам нужно создать ключ правильной формы. Для этого установите засечки нужной длины (от 1 до 3, 0 – быть не может), а затем нажмите кнопку «Попробовать». Вам будут даны 2 суждения, сколько засечек выбранной длины присутствуют в ключе (для простоты значение «наличие»), и сколько из выбранных находятся на своём месте (для простоты значение «на месте»). Скорректируйте своё решение и пробуйте, пока не подберёте ключ.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Упражнения

Сделайте все возможные умозаключения из следующих высказываний по логическому квадрату:

Сделайте обращения с теми, высказываниями, с которыми это возможно:

Проверьте, правильно ли сделаны следующие умозаключения:

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Источник