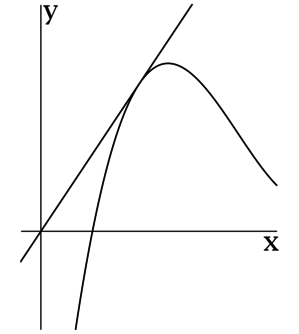Угловой коэффициент касательной что это
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.
Определения и понятия
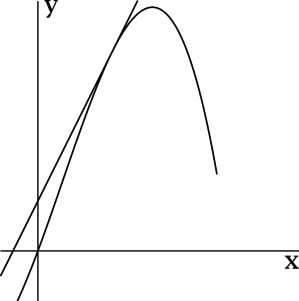
На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.
Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.
Получаем формулу для нахождения секущей вида:
По определению видно, что прямая и ее секущая в данном случае совпадают.
Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.
Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.
Геометрический смысл производной функции в точке
Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.
Уравнение касательной прямой
Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.
Решение
Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.
Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3
Отсюда следует, что α x = a r c t g 3 3 = π 6
Ответ: уравнение касательной приобретает вид
Для наглядности приведем пример в графической иллюстрации.
Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.
Решение
По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.
Перейдем к нахождению производной
Для наглядности изобразим графически.
Решение
Необходимо продифференцировать функцию. Имеем, что
Вычисляем соответствующие значения функции
Рассмотрим графическое изображение решения.
Черная линия – график функции, красные точки – точки касания.
Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что
Другое уравнение имеет два действительных корня, тогда
Перейдем к нахождению значений функции. Получаем, что
Возможно существование бесконечного количества касательных для заданных функций.
Решение
Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.
Найдены х точек касания. Теперь необходимо перейти к поиску значений у :
Ответ: необходимы уравнения запишутся как
Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.
Касательная к окружности, эллипсу, гиперболе, параболе
Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.
Касательная к окружности
Данное равенство может быть записано как объединение двух функций:
Первая функция располагается вверху, а вторая внизу, как показано на рисунке.
Касательная к эллипсу
Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что
Решение
Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид
Графически касательные обозначаются так:
Касательная к гиперболе
Гипербола может быть представлена в виде двух объединенных функций вида
Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.
Решение
Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что
Ответ: уравнение касательной можно представить как
Наглядно изображается так:
Касательная к параболе
Графически изобразим как:
Решение
Начинаем решение с представления параболы в качестве двух функций. Получим, что
Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.
Отсюда определим значение х для точек касания.
Первая функция запишется как
Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.
Вторая функция запишется как
Ответ: уравнение касательной принимает вид
Уравнение касательной к графику функции (ЕГЭ 2022)
Чтобы разобраться с этой темой, нужно знать что такое производная.
Сейчас проверим, знаешь ли ты ее… 🙂
Найди приращение функции \( y=<
Должно получиться \( \Delta y=\Delta x\left( \Delta x+2x+2 \right)\).
А теперь найди производную функции \( y\left( x \right)=3<<\sin >^<2>>\sqrt
Если в каком-нибудь из этих примеров возникли сложности, настоятельно рекомендую вернуться к теме «Производная» и проштудировать ее еще раз.
Знаю, тема очень большая, но иначе нет смысла идти дальше…
А если ты справился, то в путь!
Уравнение касательной к графику функции — коротко о главном
Геометрический смысл производной
Производная функции в конкретной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или угловому коэффициенту этой касательной:
Уравнение касательной
Уравнение касательной к графику функции \( f\left( x \right)\) в точке \( <
Алгоритм действий для нахождения уравнения касательной
| Алгоритм | Пример: \( f\left( x \right)=< |
| 1. Вычислим \( f\left( < | \( f\left( < |
| 2. Найдем формулу производной функции \( | \( |
| 3. Вычислим \( | \( |
| 4. Подставим \( < | \( \begin |
Геометрический смысл производной
Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!
Рассмотрим график какой-то функции \( y=f\left( x \right)\):
Выберем на линии графика некую точку \( A\). Пусть ее абсцисса \( <
Затем выберем близкую к точке \( A\) точку \( B\) с абсциссой \( <
Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).
Обозначим угол наклона прямой к оси \( Ox\) как \( \alpha \).
Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.
Какие значения может принимать угол \( \alpha \)?
Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – \( 180<>^\circ \), а минимально возможный – \( 0<>^\circ \).
Значит, \( \alpha \in \left[ 0<>^\circ ;180<>^\circ \right)\). Угол \( 180<>^\circ \) не включается, поскольку положение прямой в этом случае в точности совпадает с \( 0<>^\circ \), а логичнее выбирать меньший угол.
Возьмем на рисунке такую точку \( C\), чтобы прямая \( AC\) была параллельна оси абсцисс, а \( BC\) – ординат:
По рисунку видно, что \( AC=\Delta x\), а \( BC=\Delta f\).
Тогда отношение приращений:
(так как \( \angle C=90<>^\circ \), то \( \triangle ABC\) – прямоугольный).
Давай теперь уменьшать \( \Delta x\).
Тогда точка \( B\) будет приближаться к точке \( A\). Когда \( \Delta x\) станет бесконечно малым \( \left( \Delta x\to 0 \right)\), отношение \( \frac<\Delta f><\Delta x>\) станет равно производной функции в точке \( <
Что же при этом станет с секущей?
Точка \( B\) будет бесконечно близка к точке \( A\), так что их можно будет считать одной и той же точкой.
Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки \( A\), но этого достаточно).
Говорят, что при этом секущая занимает предельное положение.
Угол наклона секущей к оси \( \displaystyle Ox\) назовем \( \varphi \). Тогда получится, что производная
Производная равна тангенсу угла наклона касательной к графику функции в данной точке
Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:
За что отвечает коэффициент \( \displaystyle k\)? За наклон прямой. Он так и называется: угловой коэффициент.
Что это значит? А то, что равен он тангенсу угла между прямой и осью \( \displaystyle Ox\)!
То есть вот что получается:
Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?
Посмотрим: Теперь углы \( \alpha \) и \( \displaystyle \varphi \) тупые. А приращение функции \( \Delta f\) – отрицательное.
Получаем: \( \frac<-\Delta f><\Delta x>=-\
Снова устремим точку \( \displaystyle B\) к точке \( \displaystyle A\), и секущая \( \displaystyle AB\) примет предельное положение, то есть превратится в касательную к графику функции в точке \( \displaystyle A\).
Итак, сформулируем окончательно полученное правило:
Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:
Это и есть геометрический смысл производной.
Окей, все это интересно, но зачем оно нам? Вот пример:
На рисунке изображен график функции \( \displaystyle y=\mathsf
Найдите значение производной функции \( \displaystyle \mathsf
Решение.
Как мы недавно выяснили, значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:
\( \displaystyle f’\left( x \right)=k=\
Значит, для нахождения значения производной нам нужно найти тангенс угла наклона касательной.
На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!
Угол наклона касательной к оси \( \displaystyle Ox\) – это \( \displaystyle \angle BAC\). Найдем тангенс этого угла:
Таким образом, производная функции \( \displaystyle \mathsf
Ответ: \( \displaystyle 1,2\).
Теперь попробуй сам.
Еще статью на геометрический смысл производной ты найдешь здесь: «Геометрический смысл производной«.
Решим два примера
Пример 1. На рисунке изображен график функции \( \displaystyle y=\mathsf
Пример 2. На рисунке изображен график функции \( \displaystyle y=\mathsf
Решение примера №1
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс:
\( \displaystyle k=f’\left( x \right)=\
Достроим треугольник со стороной \( \displaystyle AC\), лежащей на касательной.
Угол наклона касательной – это угол, отмеченный зеленым на графике.
Он тупой \( \left( >90<>^\circ \right)\), поэтому его тангенс не получится вычислить так же, как в предыдущем примере (ведь в прямоугольном треугольнике не может быть тупого угла).
Применим знания из тригонометрии:
Угловой коэффициент касательной как значение производной в точке касания
\[<\large
Задачи на нахождение производной касательной включены в ЕГЭ по математике и встречаются там ежегодно. При этом статистика последних лет показывает, что подобные задания вызывают у выпускников определенные затруднения. Поэтому, если учащийся рассчитывает получить достойные баллы по итогам прохождения ЕГЭ, то ему непременно стоит научиться справляться с задачами из раздела «Угловой коэффициент касательной как значение производной в точке касания», подготовленными специалистами образовательного портала «Школково». Разобравшись с алгоритмом их решения, ученик сможет успешно преодолеть аттестационное испытание.
Основные моменты
Приступая к решению задач ЕГЭ по данной теме, необходимо вспомнить основное определение: производная функции в точке равна угловому коэффициенту касательной к графику функции в этой точке. В этом и состоит геометрический смысл производной.
Необходимо освежить в памяти и другое важное определение. Оно звучит следующим образом: угловой коэффициент равняется тангенсу угла наклона касательной к оси абсцисс.
Какие еще важные моменты стоит отметить в этой теме? При решении задач на нахождение производной в ЕГЭ необходимо помнить, что угол, который образует касательная, может быть меньше, больше 90 градусов или равняться нулю.
Как подготовиться к экзамену?
Для того, чтобы задания в ЕГЭ на тему «Угловой коэффициент касательной как значение производной в точке касания» давались вам достаточно легко, воспользуйтесь при подготовке к выпускному испытанию информацией по этому разделу на образовательном портале «Школково». Здесь вы найдете необходимый теоретический материал, собранный и понятно изложенный нашими специалистами, а также сможете попрактиковаться в выполнении упражнений.
Для каждого задания, например, задач на тему «Угловой коэффициент касательной как тангенс угла наклона», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут выполнять упражнения различного уровня сложности в режиме онлайн. В случае необходимости задачу можно сохранить в разделе «Избранное», чтобы потом обсудить ее решение с преподавателем.
Касательная к графику функции, как составить уравнение, свойства, угловой коэффициент касательной проведенной к графику функции, формула, примеры решения
На экзаменах по дисциплинам с физико-математическим уклоном или при расчетах встречается тип задач о касательной к графику функции.
Однако следует разобраться в основных терминах и соотношениях.
Специалисты рекомендуют пользоваться специальным алгоритмом, позволяющим правильно находить точку касания прямой с какой-либо фигурой.
Общие сведения
Касательной называется прямая, имеющая с фигурой или графиком заданной функции одну общую точку. Однако иногда она проходит через 2 точки. В этом случае ее называют секущей. Прямая задается следующим уравнением: y = kx + b. Значение «k» — это угловой коэффициент.
Для решения задач следует разобрать основные понятия, определения, формулы и свойства касательной.
Кроме того, очень важно понять ее геометрический смысл, поскольку без него будет сложно разобраться в более сложных дисциплинах с физико-математическим уклоном.
Определения и понятия
У касательной есть определенный параметр — угол наклона (а).
Его необходимо отсчитывать от оси абсцисс (только положительное направление) к прямой, заданной графиком y = kx + b.
От него зависит ее расположение.
Коэффициент «к» равен значению тангенса угла наклона, т. е. tg(a).
Математики сделали некоторые выводы, которые основываются на значении углового коэффициента:
В первом, втором и третьем случаях коэффициент является положительным, а в последнем — отрицательным. Эти факты следует учитывать при решении задач. Касательная прямая может являться и секущей, т. е. соприкасаться с графиком функции сразу в двух и более точках. Следует отметить, что при параллельности прямой оси ОХ (y = b), она может пересекать функцию бесконечное число раз.
Геометрический смысл
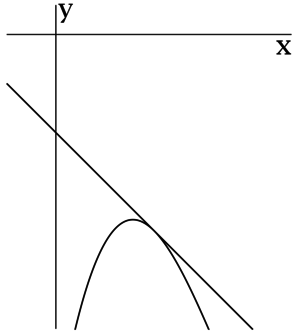
Пусть дана некоторая функция y = f(x) и секущая АВ (рис. 1). Координаты последней в точках А и В следующие: А(х0;f(x0)) и В(х0+zx;f(x0+zx)). Величина «zx» — приращение аргумента по х, которое показано стрелками. Если подставить координаты в функцию, то она имеет такой вид: zy = zf(x) = f(x0+zx) — f(zx).
Рисунок 1. Геометрический смысл.
Соотношение, которое было получено выше, называется производной. Если к графику в точке проведена секущая или касательная, то тангенс угла будет равен самой производной заданной функции в точке с координатой х0.
Из этого определения можно сделать вывод о существовании производной. Если значение последней равно 0, то, следовательно, не существует общих точек с заданной фигурой.
Касательные к фигурам и графикам
При решении задач следует обратить внимание на частные случаи. Нужно произвести расчеты уравнения прямой или найти точки соприкосновения с окружностью, эллипсом, гиперболой или параболой. Очень распространенная задача встречается также в механике о ременной передаче.
Частные случаи позволят найти оптимальное решение и метод расчета, поскольку экономия времени является важным элементом при научных исследованиях, написании контрольных работ и сдаче экзаменов. Важный этап — идентификация типа задачи. Касательная к вышеперечисленным фигурам — основной тип заданий, но существуют и более сложные функции.
Например, сложно составить уравнение прямой, которая имеет точки касания с какой-либо сложной функцией.
В некоторых случаях необходимо перед выполнением расчетов ее упростить, т. е. привести подобные слагаемые, раскрыть скобки или воспользоваться другими приемами для упрощения выражения.
Одна и несколько окружностей
Радиус, который проводится через точку касания, составляет с касательной прямой угол (перпендикулярен). Перпендикуляр к касательной, проходящий через точку касания, является радиусом или диаметром заданного круга. Из этого следует, что радиус является нормалью по отношению к прямой. Секущая — прямая, которая проходит через график или фигуру, но имеет от двух и более точек пересечения.
Формула окружности с центром в точке О (xc;yc) и радиусом R имеет следующий вид: sqr(х-хc) + sqr(y-yc) = R^2.
Для решения следует выразить значение у, но при этом нужно рассматривать 2 случая:
Две функции являются полукругами и вместе образуют окружность. Чтобы составить график круга в точке (х0;у0), нужно уравнение в этой точке. В точках с координатами (хц;yц+R) и (хц;yц-R) уравнения касательных к окружности задаются следующими уравнениями: y = yц + R и y = yц — R. Если взять точки (хц+R;yц) и (хц-R;yц), они будут иметь такую форму: x = xц + R и x = xц — R.
В случае для двух окружностей всего можно провести до 4 касательных (2 внешних и 2 внутренних). Это зависит от случая расположения фигур. Точкой пересечения внешних считается внешняя гомотетия (подобие), а внутренних — в центре внутреннего подобия. Внешними называются прямые, которые касаются внешних точек круга. Если касательные являются внутренними, то они пересекают линию, соединяющую центры окружностей.
Следует отметить, что внешний и внутренний центры гомотетии лежат на некоторой прямой. Она проходит через центры заданных окружностей. Это был рассмотрен случай, когда одна окружность меньше другой.
Однако при равенстве их диаметров появляются некоторые свойства: внешние касательные параллельны и внешнего центра гомотетии не существует.
Основные соотношения можно вывести, используя уравнение прямой (касательной) и расстояние от точки до прямой. Пусть окружности с радиусами R1 и R2 имеют следующие координаты центров: с1(х1;у1) и с2(х2;у2). Уравнение прямой записывается таким образом: ах + by + c = 0. Расстояния до прямой от точек с1 и с2 вычисляются таким образом: ах1 + by1 + c = R1 и ах2 + by2 + c = R2. Формула находится с помощью вычитания первого уравнения из второго: а(х2 — х1) + b(y2 — у1) = R2 — R1. Следовательно, расстояние вычисляется по следующей формуле: d = sqrt[(х2 — х1)^2 + (y2 — у1)^2].
Эллипс, гипербола и парабола
Пусть задан эллипс с полуосями a и b.
В первом случае прямые параллельны оси ординат, а во втором — абсцисс. Чтобы написать уравнение прямой, нужно определить, к какой из функций принадлежит точка, выполнив подстановку в текущие равенства. После этого их следует проверить на тождественность.
Чтобы записать уравнение прямой-касательной к параболе y = ax^2 + bx + c в точке с координатами (x0;y(x0)), нужно привести равенство к следующему виду: y = y'(x0) * (x-x0) + y(x0). Из формулы можно сделать вывод о том, что прямая параллельна оси абсцисс. Параболу нужно рассматривать, как объединение двух функций (x = ay^2 + by + c). Рекомендуется решить его относительно y. Дискриминант вычисляется таким образом: D = b^2 — 4a(c — x).
В зависимости от его значения находятся корни:
Существует несколько типов задач на нахождение уравнения прямой, которая соприкасается с заданным графиком функции. Самой простой является задача со следующей формулировкой: прямая является касательной к графику функции. Найдите все точки касания. В этом случае задается уравнение графика функции и прямой. Некоторые задания считаются более сложными. В них необходимо написать уравнение касательной или касательных.
Рекомендации специалистов
Для решения задачи нужно внимательно прочитать условие и выяснить величины, которые следует найти. Все построено на нахождении производной функции. После этого нужно подставить значение координат точки в выражение первообразной. В некоторых случаях функция задается параметрически. Для удобства ее рекомендуется перевести в каноническую форму.
Рекомендуется разбивать задачу на несколько подзадач, поскольку будет очень просто выполнить проверку и исправить найденные ошибки. Существует несколько способов нахождения уравнения касательной: автоматизированный и ручной. В первом случае нужно использовать программное обеспечение. Оптимальным решением проблемы является онлайн-калькулятор.
При ручном режиме нужно решать, а иногда выполнить построение графика. Для оптимизации вычислений можно использовать Excel. График должен быть качественно построен и предельно понятен. В некоторых случая нужно будет вычислять предельные значения используя границы (lim).
Упражнения и ход вычислений
Нужно написать уравнение прямой-касательной к y(x) = x^3 — 2x^2 + 3 в т. xо = 2. Следует воспользоваться следующим алгоритмом:
Одним из типов задач является нахождение точек, лежащих на ОХ, в которых прямые (касательные) || OX. Задана функция f(x) = x^3 — x^2 — 3x + 7. Угол наклона равен 0 градусов, т. к. касательная || OX (производная в точках касания равна 0).
Алгоритм решения следующий:
Рекомендуется оставить в таком виде, поскольку при вычислении кубического корня появятся некоторые погрешности. В этих примерах необязательно составление графика.
Таким образом, геометрический смысл уравнения касательной к функции — производная. Следует изучить основные понятия, формулы и разобрать решение типовых задач. Также нужно повторить таблицу производных функций.