при каких условиях можно использовать формулу эйлера для расчета критической силы
Определение критической силы. Формула Эйлера
Впервые проблема устойчивости сжатых стержней была поставлена Леонардом Эйлером. Эйлер вывел расчетную формулу для критической силы и показал, что ее величина существенно зависит от способа закрепления стержня. Идея метода Эйлера заключается в установлении условий, при которых кроме прямолинейной возможна и смежная (т.е. сколь угодно близкая к исходной) криволинейная форма равновесия стержня при постоянной нагрузке.

В теории продольного изгиба принято сжимающую силу считать положительной. Поэтому, определяя изгибающий момент в текущем сечении рассматриваемого стержня, получаем

Но, как следует из рис. 13.4, при выбранном направлении осей у // у на противоположное, то одновременно изменятся знаки у и у // и знак минус в правой части уравнения (13.2) сохранится.
Следовательно, уравнение упругой линии стержня имеет вид


общий интеграл которого

Горизонтальное смещение нижнего конца стержня, как видно из рис. 13.4, равно нулю, т. е. при х =0 прогиб у =0. Это условие будет выполнено, если B =0. Следовательно, изогнутая ось стержня является синусоидой

Горизонтальное смещение верхнего конца стержня также равно нулю, поэтому



Приравнивая α l = n π и подставляя


Величина наибольшего прогиба стержня A в приведенном решении остается неопределенной, она принята произвольной, но предполагается малой.
Выше мы установили, что изогнутая ось стержня является синусоидой, уравнение которой после подстановки α = π n / l в выражение (13.4) принимает вид

Синусоиды для n =1, n =2 изображены на рис. 13.5. Нетрудно заметить, что величина n представляет собой число полуволн синусоиды, по которой изогнется стержень. Очевидно, стержень всегда изогнется по наименьшему числу полуволн, допускаемому его опорными устройствами, так как согласно (13.5) наименьшему n соответствует наименьшая критическая сила. Только эта первая критическая сила и имеет реальный физический смысл.
Например, стержень с шарнирно опертыми концами изогнется, как только будет достигнуто наименьшее значение критической силы, соответствующее n =1, так как опорные устройства этого стержня допускают изгиб его по одной полуволне синусоиды. Критические силы, соответствующие n =2, n =3, и более, могут быть достигнуты только при наличии промежуточных опор (рис. 13.6). Для стержня с шарнирными концевыми опорами без промежуточных закреплений реальный смысл имеет первая критическая сила

Формула (13.5), как следует из ее вывода, справедлива не только для стержня с шарнирно закрепленными концами, но и для любого стержня, который изогнется при выпучивании по целому числу полуволн. Применим эту формулу, например, при определении критической силы для стержня, опорные устройства которого допускают только продольные смещения его концов (стойка с заделанными концами). Как видно из рисунка 13.7, число полуволн изогнутой оси в этом случае n =2 и, следовательно, критическая сила для стержня при данных опорных устройствах

Эту формулу можно записать в виде

Рассмотрим далее пример, чтобы показать, какой вид имеет выражение для критической силы в случаях, когда стойка выпучивается не по целому числу полуволн синусоиды.
Дифференциальное уравнение изогнутой оси стойки в изображенной на рис. 13.8 системе координатных осей имеет прежний вид.
Общее решение этого уравнения:

Мы предположили, что стойка изогнута, поэтому величина A не может быть равна нулю. Следовательно, cos α l = 0. Наименьший отличный от нуля, корень этого уравнения α l = π /2 определяет первую критическую силу

которой соответствует изгиб стержня по синусоиде

Значениям α l =3 π /2, α l =5 π /2 и т.д, как было показано выше, соответствуют большие величины P k и более сложные формы изогнутой оси стойки, которые могут практически существовать лишь при наличии промежуточных опор.

Дифференциальное уравнение упругой линии

Общее решение этого уравнения имеет вид

При x =0 прогиб у =0, следовательно, B =0.
При x = l угол поворота сечения равен нулю, поэтому y / ( l )=0. Из этого условия получаем

Итак, имеем следующее уравнение упругой линии стержня:

Условие y ( l )=0 будет выполнено, если

Отсюда получаем следующее трансцендентное разрешающее уравнение для определения величины α :


Сопоставляя формулы (13.7), (13.8), (13.9) и (13.10), нетрудно заметить, что все они имеют одинаковое строение, и их можно обобщить на случай любых опорных устройств стойки, если записать формулу Эйлера в виде

Коэффициенты приведения μ для некоторых стоек даны на рис. 17.10.
Пределы применимости формулы Эйлера
Формула Эйлера выполняется только в пределах упругих деформаций.
Таким образом, критическое напряжение должно быть меньше предела упругости материала.
Предельная гибкость зависит от материала стержня.
Критическую силу при расчете критического напряжения по формуле Ясинского можно определить как
Условие устойчивости:
Контрольные вопросы и задания
1. Какое равновесие называется устойчивым?
2. Какие брусья следует рассчитывать на устойчивость?
3. Какую силу при расчете на устойчивость называют критической?
4. Напишите формулу Эйлера для расчета критической силы и назовите входящие величины и их единицы измерения.
5. Что называют гибкостью стержня, какой смысл заложен в этом названии? Назовите категории стержней в зависимости от гибкости.
6. От каких параметров стержня зависит предельная гибкость?
7. При каких условиях можно использовать формулу Эйлера для расчета критической силы?
8. В чем заключается расчет сжатого стержня на устойчивость? Напишите условие устойчивости. Чем отличается допускаемая сжимающая сила от критической?
Тема 2.10. Устойчивость сжатых стержней 295
Тема 2.10. Устойчивость сжатых стержней.
Расчеты на устойчивость
Знать условие устойчивости сжатых стержней, формулы Эйлера для определения критической силы, эмпирические формулы для расчетов критического напряжения и критической силы.
Уметь выполнять проверочные расчеты на устойчивость сжатых стержней.
Порядок выполнения расчета на устойчивость
1.Получение сведений о материале стержня для определения
предельной гибкости стержня расчетным путем или по таблице:
2. Получение сведений о геометрических размерах поперечного сечения, длине и способах закрепления концов для определения категории стержня в зависимости от гибкости:
где А — площадь сечения; Jmin— минимальный момент инерции (из осевых);
μ — коэффициент приведенной длины.
3. Выбор расчетных формул для определения критической силы
и критического напряжения.
При λ0 λ пред — расчет по формуле Эйлера.
4. Проверка и обеспечение устойчивости.
При расчете по формуле Эйлера условие устойчивости:
F — действующая сжимающая сила; [ sy ] — допускаемый коэффициент запаса устойчивости.
В случае невыполнения условий устойчивости необходимо увеличить площадь поперечного сечения.
Иногда необходимо определить запас устойчивости при заданном нагружении:
При проверке устойчивости сравнивают расчетный запас выносливости с допускаемым:
Примеры решения задач
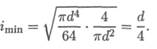
Пример 1. Рассчитать гибкость стержня. Круглый стержень диаметром 20 мм закреплен так, как показано на рис. 37.1.
Решение
1. Гибкость стержня определяется по формуле
2. Определяем минимальный радиус инерции для круга.
Тема 2.10. Устойчивость сжатых стержней 297
Подставив выражения для Jmin и А (сечение — круг)
получим
3. Коэффициент приведения длины для данной схемы крепления μ = 0,5.
4. Гибкость стержня будет равна
Пример 2. Как изменится критическая сила для стержня, если изменить способ закрепления концов? Сравнить представленные схемы (рис. 37.2)
Решение
Критическая сила увеличится в 4 раза. FKP2 = 4FKPl.
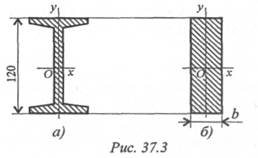
Пример 3. Как изменится критическая сила при расчете на устойчивость, если стержень двутаврового сечения (рис. 37.3а, двутавр № 12) заменить стержнем прямоугольного сечения той же площади (рис. 37.3b)? Остальные параметры конструкции не меняются. Расчет выполнить по формуле Эйлера.
Решение
1. Определим ширину сечения прямоугольника, высота сечения
равна высоте сечения двутавра. Геометрические параметры двутавра № 12 по ГОСТ 8239-89 следующие:
площадь сечения А1= 14,7 см 2 ;
По условию площадь прямоугольного сечения равна площади сечения двутавра. Определяем ширину полосы при высоте 12 см.
2. Определим минимальный из осевых моментов инерции.
3. Критическая сила определяется по формуле Эйлера:
4. При прочих равных условиях отношение критических сил равно отношению минимальных моментов инерции:
5. Таким образом, устойчивость стержня с сечением двутавр
№ 12 в 15 раз выше, чем устойчивость стержня выбранного прямоугольного сечения.
Тема 2.10. Устойчивость сжатых стержней 299
Пример 4. Проверить устойчивость стержня. Стержень длиной 1м защемлен одним концом, сечение — швеллер № 16, материал — СтЗ, запас устойчивости трехкратный. Стержень нагружен сжимающей силой 82 кН (рис. 37.4).
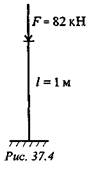
1. Определяем основные геометрические пара метры сечения стержня по ГОСТ 8240-89.
Швеллер № 16: площадь сечения 18,1см 2 ; минимальный осевой момент сечения 63,3 см 4 ; минимальный радиус инерции сечения imin = 1,87 см.
2. Определяем категорию стержня в зависимости от гибкости.
Предельная гибкость для материала СтЗ λпред = 100.
Расчетная гибкость стержня при длине l = 1м = 1000мм
Рассчитываемый стержень — стержень большой гибкости, расчет ведем по формуле Эйлера.
3. Допускаемая нагрузка на стержень [ F ] = FKp / [ sy ].
Дата добавления: 2019-09-13 ; просмотров: 1290 ; Мы поможем в написании вашей работы!
Техническая механика
Сопротивление материалов
Расчеты на устойчивость при продольном изгибе
Понятие продольного изгиба
Продольным изгибом называется изгиб первоначально прямолинейного стержня вследствие потери устойчивости под действием центрально приложенных продольных сжимающих сил. Продольный изгиб возникает при достижении сжимающими силами и напряжениями критического значения.
Расчеты на прочность и жесткость, выполняемые для большинства видов деформаций основываются на предположении, что между внешними нагрузками и вызываемыми ими внутренними силами существует устойчивая форма равновесия, при которой малым возмущающим воздействиям соответствуют малые отклонения конструкции от первоначальной формы.
Нагрузки, при превышении которых происходит потеря устойчивости (критическое состояние), называют критическими нагрузками.
Примером явления продольного изгиба может послужить длинная школьная линейка, к одному из концов которой приложена сжимающая сила. Сначала материал линейки сопротивляется нагрузке, и линейка работает, как обычный сжимаемый брус. Затем, по достижении определенной нагрузки, линейка начинает прогрессирующе изгибаться без существенного увеличения сжимающей силы и теряет устойчивость (т. е. гнется без заметных усилий вплоть до поломки).
Если предположить, что материал стержня идеально соответствует принимаемым в сопромате допущениям и гипотезам, а сжимающая сила приложена строго к центру тяжести сечения вдоль оси стержня, то такой стержень будет работать на простое сжатие, и разрушится не из-за потери устойчивости, а из-за превышения предельных прочностных характеристик для сжатия. Если же стержень имеет сечение в виде сложной фигуры, то решающую роль при потере устойчивости играет отклонение продольной нагрузки от главной центральной оси этой фигуры.
Опасность потери устойчивости особенно велика для тонкостенных конструкций, стержней, пластинок и оболочек.
Таким образом, искривленный стержень испытывает сочетание деформаций центрального сжатия и изгиба.
При сжимающих силах, даже немного превышающих критическую силу, напряжения изгиба могут непосредственно угрожать прочности конструкции. Поэтому критическое состояние конструкции считается недопустимым.
где: [sy] – допускаемый коэффициент запаса устойчивости.
Очевидно, что устойчивость стержня обеспечена, если [sy] > 1.
Значение коэффициента запаса устойчивости зависит от назначения стержня и его материала. Обычно для сталей [sy] = 1,8….3; для чугунов [sy] = 5….5,5; для дерева [sy] = 2,8….3,2.
Формулы Эйлера и Ясинского для расчетов стержней на устойчивость
Первые исследования устойчивости сжатых стержней были проведены академиком Петербургской Академии наук Леонардом Эйлером (1707-1783 г.г.). В дальнейшем большая работа в области теоретического и экспериментального следования вопросов устойчивости была проведена русским ученым, профессором Петербургского института инженеров путей сообщения Ф. С. Ясинским (1856-1899 г.г.), опубликовавшим в 1893 году научную работу «Опыт развития продольного изгиба».
Л. Эйлер почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. С 1726 по 1741, а также с 1766 года и до конца жизни был академиком Петербургской академии наук. С 1741 по 1766 год работал в Берлине (оставаясь одновременно почётным членом Петербургской академии).
Превосходно знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском.
Некоторые из потомков Л. Эйлера до сих пор живут в России.
где: l – длина стержня; μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня.
Определим наименьший радиус инерции imin поперечного сечения стержня:
Перепишем формулу для σкр так:
Формулу Эйлера можно применять только при выполнении условия:
где: σпц – предел пропорциональности материала стержня. Следовательно, должно быть
В тех случаях, когда гибкость стержней меньше предельной, формула Эйлера становится неприменимой и при расчетах пользуются эмпирической формулой Ясинского:
где: а и b – коэффициенты, зависящие от материала и определяемые по таблицам справочников.
Расчеты прямолинейных стержней на устойчивость
Существует три вида расчетов на устойчивость прямолинейных стержней – проектный, проверочный и силовой.
Проектный расчет заключается в определении минимального осевого момента инерции поперечного сечения стержня по формуле:
Полученную гибкость сравнивают с предельной для данного материала.
Проверочный расчет заключается в определении действительного коэффициента запаса устойчивости sy и сравнении его с допускаемым:
Силовой расчет заключается в определении допускаемой нагрузки [F] по формуле:
Расчет сжатых стержней на устойчивость можно свести к расчету на простое сжатие. При расчете применяют следующую формулу:
где: [σс] – допускаемое напряжение на сжатие; φ – коэффициент продольного изгиба (справочная величина, определяемая по таблицам).
Расчеты показывают, что при продольном изгибе наиболее выгодными являются кольцевые и коробочные тонкостенные сечения, имеющие относительно большой момент инерции.
При каких условиях можно использовать формулу эйлера для расчета критической силы
Во всем предыдущем изложении мы определяли поперечные размеры стержней из условий прочности. Однако разрушение стержня может произойти не только потому, что будет нарушена прочность, но и оттого, что стержень не сохранит той формы, которая ему придана конструктором; при этом изменится и характер напряженного состояния в стержне.
Наиболее типичным примером является работа стержня, сжатого силами Р. До сих пор для проверки прочности мы имели условие
Это условие предполагает, что стержень все время, вплоть до разрушения работает на осевое сжатие. Уже простейший опыт показывает, что далеко не всегда возможно разрушить стержень путем доведения напряжений сжатия до предела текучести или до предела прочности материала.
Если мы подвергнем продольному сжатию тонкую деревянную линейку, то она может сломаться, изогнувшись; перед изломом сжимающие силы, при которых произойдет разрушение линейки, будут значительно меньше тех, которые вызвали бы при простом сжатии напряжение, равное пределу прочности материала. Разрушение линейки произойдет потому, что она не сможет сохранить приданную ей форму прямолинейного, сжатого стержня, а искривится, что вызовет появление изгибающих моментов от сжимающих сил Р и, стало быть, добавочные напряжения от изгиба; линейка потеряет устойчивость.
Поэтому для надежной работы конструкции мало, чтобы она была прочна; надо, чтобы все ее элементы были устойчивы: они должны при действии нагрузок деформироваться в таких пределах, чтобы характер их работы оставался неизменным. Поэтому в целом ряде случаев, в частности, для сжатых стержней, помимо проверки на прочность, необходима и проверка на устойчивость. Для осуществления этой проверки надо ближе ознакомиться с условиями, при которых устойчивость прямолинейной формы сжатого стержня нарушается.
Рис.1. Расчетная схема
Возьмем достаточно длинный по сравнению с его поперечными размерами стержень, шарнирно-прикрепленный к опорам (Рис.1), и нагрузим его сверху центрально силой Р, постепенно возрастающей. Мы увидим, что пока сила Р сравнительно мала, стержень будет сохранять прямолинейную форму. При попытках отклонить его в сторону, например путем приложения кратковременно действующей горизонтальной силы, он будет после ряда колебаний возвращаться к первоначальной прямолинейной форме, как только будет удалена добавочная сила, вызвавшая отклонение.
При постепенном увеличении силы Р стержень будет все медленнее возвращаться к первоначальному положению при проверках его устойчивости; наконец, можно довести силу Р до такой величины, при которой стержень, после небольшого отклонения его в сторону, уже не выпрямится, а останется искривленным. Если мы, не удаляя силы Р, выпрямим стержень, он уже, как правило, не сможет сохранить прямолинейную форму. Другими словами, при этом значении силы Р, называемом критическим 
Переход к критическому значению силы Р происходит внезапно; стоит нам очень немного уменьшить сжимающую силу по сравнению с ее критической величиной, как прямолинейная форма равновесия вновь делается устойчивой.
С другой стороны, при очень небольшом превышении сжимающей силой Р ее критического значения прямолинейная форма стержня делается крайне неустойчивой; достаточно при этом небольшого эксцентриситета приложенной силы, неоднородности материала по сечению, чтобы стержень искривился, и не только не вернулся к прежней форме, а продолжал искривляться под действием все возрастающих при искривлении изгибающих моментов; процесс искривления заканчивается либо достижением совершенно новой (устойчивой) формы равновесия, либо разрушением.
Исходя из этого, мы должны практически считать критическую величину сжимающей силы 
Обычно подобная возможность является исключением; поэтому практически следует считать критическую сжимающую силу низшим пределом «разрушающей» стержень силы.
Рис.2. Аналогия понятия устойчивости из механики твердого тела
Явление потери устойчивости при сжатии можно по аналогии иллюстрировать следующим примером из механики твердого тела (рис.2). Будем вкатывать цилиндр на наклонную плоскость ab, которая потом переходит в короткую горизонтальную площадку bс и наклонную плоскость обратного направления cd. Пока мы поднимаем цилиндр по плоскости ab, поддерживая его при помощи упора, перпендикулярного к наклонной плоскости, он будет в.состоянии устойчивого равновесия; на площадке bс его равновесие делается безразличным; стоит же нам поместить цилиндр в точку с, как его равновесие сделается неустойчивым при малейшем толчке вправо цилиндр начнет двигаться вниз.
Описанную выше физическую картину потери устойчивости сжатым стержнем легко осуществить в действительности в любой механической лаборатории на очень элементарной установке. Это описание не является какой-то теоретической, идеализированной схемой, а отражает поведение реального стержня под действием сжимающих сил.
Потерю устойчивости прямолинейной формы сжатого стержня иногда называют «продольным изгибом», так как она влечет за собой значительное искривление стержня под действием продольных сил. Для проверки на устойчивость сохранился и до сих пор термин «проверка на продольный изгиб», являющийся условным, так как здесь речь должна идти не о проверке на изгиб, а о проверке на устойчивость прямолинейной формы стержня.
Установив понятие о критической силе, как о «разрушающей» нагрузке, выводящей стержень из условий его нормальной работы, мы легко можем составить условие для проверки на устойчивость, аналогичное условию прочности.
Критическая сила 


где 

Для возможности осуществить проверку на устойчивость мы должны показать, как определять 

Формула Эйлера для определения критической силы.
Для нахождения критических напряжений 

Эту задачу впервые решил академик Петербургской Академии наук Л. Эйлер в 1744 году.
Заметим, что самая постановка задачи иная, чем во всех ранее рассмотренных отделах курса. Если раньше мы определяли деформацию стержня при заданных внешних нагрузках, то здесь ставится обратная задача: задавшись искривлением оси сжатого стержня, следует определить, при каком значении осевой сжимающей силы Р такое искривление возможно.
Рассмотрим прямой стержень постоянного сечения, шарнирно опертый по концам; одна из опор допускает возможность продольного перемещения соответствующего конца стержня (рис.3). Собственным весом стержня пренебрегаем.
Рис.3. Расчетная схема в «задаче Эйлера»
Нагрузим стержень центрально приложенными продольными сжимающими силами 

Деформация изгиба стержня предположена весьма малой, поэтому для решения поставленной задачи можно воспользоваться приближенным дифференциальным уравнением изогнутой оси стержня. Выбрав начало координат в точке А и направление координатных осей, как показано на рис.3, имеем:
Возьмем сечение на расстоянии х от начала координат; ордината изогнутой оси в этом сечении будет у, а изгибающий момент равен
По исходной схеме изгибающий момент получается отрицательным, ординаты же при выбранном направлении оси у оказываются положительными. (Если бы стержень искривился выпуклостью книзу, то момент был бы положительным, а у отрицательным и 
Приведенное только что дифференциальное уравнение принимает вид:
деля обе части уравнения на EJ и обозначая дробь 

Общий интеграл этого уравнения имеет вид:
Это решение заключает в себе три неизвестных: постоянные интегрирования а и b и значение 
Краевые условия на концах стержня дают два уравнения:
в точке А при х = 0 прогиб у = 0,
Из первого условия следует (так как 
Таким образом, изогнутая ось является синусоидой с уравнением
Применяя второе условие, подставляем в это уравнение
Отсюда следует, что или а или kl равны нулю.
Если а равно нулю, то из уравнения (2) следует, что прогиб в любом сечении стержня равен нулю, т. е. стержень остался прямым. Это противоречит исходным предпосылкам нашего вывода. Следовательно, sin kl = 0, и величина 
где 
Отсюда 


Иначе говоря, нагрузка, способная удержать слегка искривленный стержень в равновесии, теоретически может иметь целый ряд значений. Но так как отыскивается, и интересно с практической точки зрения, наименьшее значение осевой сжимающей силы, при которой становится возможным продольный изгиб, то следует принять 
Первый корень 


(Здесь Jминимальный момент инерции поперечного сечения стержня.) Это так называемая формула Эйлера для сжатого стержня с шарнирно-опертыми концами. Значению критической силы (3) соответствует изгиб стержня по синусоиде с одной полуволной [формула (2)]






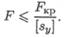
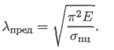
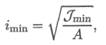
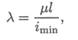
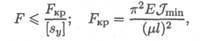
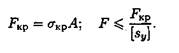
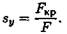
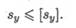
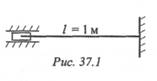
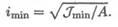
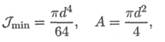
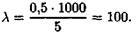

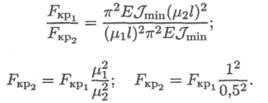
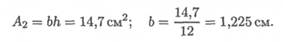
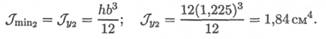
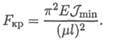
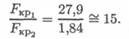
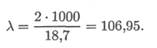
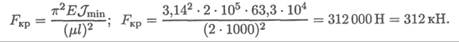
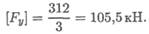

















Warning: Use of undefined constant expert_review_likes - assumed 'expert_review_likes' (this will throw an Error in a future version of PHP) in /var/www/www-ars1963/data/www/ck62.ru/wp-content/themes/colormag/comments.php on line 93