по какому алгоритму вводимые в компьютер десятичные числа можно перевести
Как проводится перевод числа из десятичной системы в двоичную?
Содержание:
Перевод из десятичной в двоичную систему исчисления проводится несложно. Для этого действия есть собственный специализированный алгоритм, который мы рассмотрим чуть ниже.
Перевод из десятичной в двоичную систему: целые числа
Пример, как осуществляется перевод из десятичной в двоичную систему
Перевод из десятичной в двоичную систему: дробные числа
Здесь тоже не все может быть сразу понятно, но взглянув на пример, все сразу станет ясно.
Пример, как осуществляется перевод дробного десятичного числа в двоичную систему
Эту конвертацию можно осуществлять до того момента, пока мы не добьемся нужного уровня погрешности. Но для демонстрации алгоритма конвертации этого достаточно. В результате мы получили, что десятичное число 0,234 в двоичном исчислении будет равняться 0011101111100.
А как конвертировать дробное число, если у него в целой части будет какое-то другое значение, кроме 0? Например нам нужно конвертировать число 10,25. В этом случае целая и дробная части будут переводиться раздельно:
Вот что мы получим по факту:
В конце наших вычислений мы получим, что десятичное число 10,25 в двоичной форме будет выглядеть вот так — 1010,01. Кстати, если внимательно посмотреть, то видно, что при конвертации в двоичную форму дробной части нашего примера (при умножении на 2), дробная часть стала равняться 0, поэтому вычисления закончились.
Перевод из десятичной системы счисления в двоичную
Перед тем как перейти к алгоритму перевода, вспомним алфавит двоичной и десятичной системы счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 2 | Двоичная | 0, 1 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Для перевода чисел из десятичной системы в двоичную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода целых десятичных чисел в двоичную систему счисления
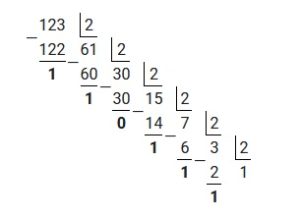
Пример 1 : перевести десятичное число 123 в двоичную систему счисления
Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:
Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.
Алгоритм перевода десятичной дроби в двоичную систему
Пример 2: перевести число 0,123 в двоичную систему.
Решение будет выглядеть следующим образом:
0.123 ∙ 2 = 0.246 (0)
0.246 ∙ 2 = 0.492 (0)
0.492 ∙ 2 = 0.984 (0)
0.984 ∙ 2 = 1.968 (1)
0.968 ∙ 2 = 1.936 (1)
0.936 ∙ 2 = 1.872 (1)
0.872 ∙ 2 = 1.744 (1)
0.744 ∙ 2 = 1.488 (1)
0.488 ∙ 2 = 0.976 (0)
0.976 ∙ 2 = 1.952 (1)
0.952 ∙ 2 = 1.904 (1)
В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.
Перевод дробного десятичного числа в двоичную систему
Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.
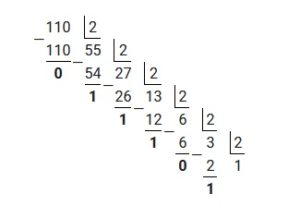
Пример 3: перевести число 110,625 из десятичной системы в двоичную
Для решения примера потребуется отдельно перевести 110 и отдельно 0,625 из десятичной системы в двоичную, используя вышеизложенные алгоритмы. Таким образом переведя 110, получим:
Перевод десятичной дроби 0,625 выглядит так:
0.625 ∙ 2 = 1.25 (1)
0.25 ∙ 2 = 0.5 (0)
0.5 ∙ 2 = 1 (1)
Теперь осталось соединить результаты перевода. Таким образом: 110.62510=1101110.1012
Обратите внимание, что данный пример наглядно демонстрирует ситуацию, при которой дробная часть стала равной 0 и дальнейшее вычисление закончилось.
Как переводить числа с запятой
Перевод дробных чисел из одной системы счисления в другую
После того, как я сделал несколько калькуляторов для перевода между разными системами счисления — вот список от первой до последней версии, от самого простого к сложному: Перевод числа в другие системы счисления, Перевод из десятичной системы счисления, Перевод из одной системы счисления в другую — в комментариях стали периодически спрашивать — а что же, мол, дробные числа, как же их переводить? И когда спросили больше трех раз, я таки решил изучить этот вопрос.
Результатом стал калькулятор, который вы видите ниже, он умеет переводить и дробные числа в том числе. Как водится, для любознательных под калькулятором немного теории.
Перевод дробных чисел из одной системы счисления в другую
Теперь теория. Я, честно говоря, думал, что вопрос довольно сложный, но при ближайшем рассмотрении все оказалось проще простого. Надо было только держать в голове тот факт, что речь идет о позиционных системах счисления.
В чем тут суть? Рассмотрим на примере десятичного числа 6.125. Это дробное число в десятичной системе счисления представляется так:
Все просто, не так ли? Та же самая простота сохраняется и при записи дробного числа в любой другой системе счисления. Возьмем, например, горячо любимую каждым программистом двоичную систему и число, например, 110.001. Эта запись есть не что иное как
Да-да, число для примера было выбрано не просто так. То есть, 110.001 в двоичной системе есть 6.125 в десятичной. Принцип, я думаю, ясен.
Есть только одно но — все-таки из-за того, что здесь участвую дроби с разными знаменателями, не всегда одно и тоже число можно одинаково точно выразить в разных системах счисления. Что я имею в виду?
Продолжать можно еще довольно долго, но уже сейчас видно, что 0.8 в десятичной системе это 0.11001100. (дальше очень много цифр) в двоичной. Если честно, то это периодическое число с перидом 1100, так что мы никогда не сможем выразить его точно в двоичной системе счисления. 110011001100. будет продолжаться до бесконечности.
Поэтому перевод дробного числа из одной системы счисления в другую чаще всего дает погрешность. Погрешность эта зависит от того, сколько разрядов мы используем для записи дробной части переведенного числа. Возьмем пример с числом 0.8 и используем для записи его двоичного представления шесть разрядов после запятой — 0.110011. Полученное число вовсе не 0.8, а 0.796875, разница при этом составляет 0.003125. Это и есть наша погрешность перевода десятичного числа 0.8 в двоичный вид при использовании шести разрядов после запятой.
Нужно перевести число 1011010.101 в десятичную систему. Запишем это число следующим образом:
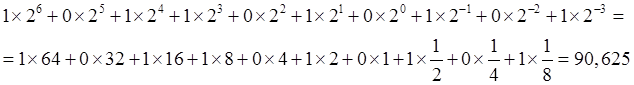
Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:
Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.
Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:
.116 • 2 = 0.232
.232 • 2 = 0.464
.464 • 2 = 0.928
.928 • 2 = 1.856
.856 • 2 = 1.712
.712 • 2 = 1.424
.424 • 2 = 0.848
.848 • 2 = 1.696
.696 • 2 = 1.392
.392 • 2 = 0.784
и т. д.
Получим: 206,11610=11001110,00011101102
· Преобразование восьмеричных чисел в десятичные.
Алгоритм перевода чисел из восьмеричной в десятичную систему счисления аналогичен уже рассматривавшему мною в разделе: Преобразование двоичных чисел в десятичные.
Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет[1] двоичных цифр.
Пример: 25418 = 010 101 100 001 = 0101011000012
Существует таблица перевода восьмеричных чисел в двоичные
| 8 | = | 0002 |
| 18 | = | 0012 |
| 28 | = | 0102 |
| 38 | = | 0112 |
| 48 | = | 1002 |
| 58 | = | 1012 |
| 68 | = | 1102 |
| 78 | = | 1112 |
· Преобразование шестнадцатеричных чисел в десятичные.
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316 = 3·16 0 +10·16 1 +5·16²= 3·1+10·16+5·256= 3+160+1280= 144310
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
0101101000112 = 0101 1010 0011 = 5A316
Таблица перевода чисел
| 16=010=08 |
| 116=110=18 |
| 216=210=28 |
| 316=310=38 |
| 416=410=48 |
| 516=510=58 |
| 616=610=68 |
| 716=710=78 |
| 816=810=108 |
| 916=910=118 |
| A16=1010=128 |
| B16=1110=138 |
| C16=1210=148 |
| D16=1310=158 |
| E16=1410=168 |
| F16=1510=178 |
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9467 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Пример
44(10) переведём в двоичную систему
44 делим на 2. частное 22, остаток 0
22 делим на 2. частное 11, остаток 0
11 делим на 2. частное 5, остаток 1
5 делим на 2. частное 2, остаток 1
2 делим на 2. частное 1, остаток 0
1 делим на 2. частное 0, остаток 1
Частное равно нулю, деление закончено. Теперь записав все остатки снизу вверх получим число 101100(2)
Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в нуль и начать умножение получившегося числа на основание той системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в нуль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль. Ниже приводится пример перевода числа 103,625(10) в двоичную систему счисления.
Переводим целую часть по правилам, описанным выше, получаем 103(10) = 1100111(2).
0,625 умножаем на 2. Дробная часть 0,250. Целая часть 1.
0,250 умножаем на 2. Дробная часть 0,500. Целая часть 0.
0,500 умножаем на 2. Дробная часть 0,000. Целая часть 1.
Итак, сверху вниз получаем число 101(2)
103,625(10) = 1100111,101(2)
Точно также осуществляется перевод в системы счисления с любым основанием.
Сразу нужно отметить, что этот пример специально подобран, в общем случае очень редко удаётся завершить перевод дробной части числа из десятичной системы в другие системы счисления, а потому, в подавляющем большинстве случаев, перевод можно осуществить с какой либо долей погрешности. Чем больше знаков после запятой — тем точнее приближение результата перевода к истине. В этих словах легко убедиться, если попытаться, например, перевести в двоичный код число 0,626.
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Программирование перевода чисел из одной системы счисления в другую
Основные темы параграфа:
■ перевод двоичного числа в десятичную систему счисления;
■ перевод десятичного числа в двоичную систему счисления.
В§ 18 учебника для 8 класса рассказано о двоичной системе счисления, которая используется в компьютере для представления чисел и выполнения вычислений с ними. Там же описаны правила, по которым можно вручную выполнить перевод двоичных чисел в десятичную систему счисления и обратный перевод — десятичных чисел в двоичные. Рассмотрим программы на Паскале для автоматического перевода чисел из одной системы счисления в другую. Ограничимся переводом целых чисел.
Программа перевода двоичного числа в десятичную систему счисления
Рассмотрим программу на Паскале, по которой происходит перевод целого двоичного числа в десятичную систему.
ProgramNumbers_2_l0;
varN10,N2,k: longint;
Begin
while(N2<>0)do
Begin
N10:=N10 + (N2 mod 10)*k;
N2:=N2 div 10
В программе использованы следующие переменные:
N2 — целое двоичное число — исходное данное;
N10 — десятичное число — результат;
В этой программе используются две незнакомые вам операции с целыми числами. Операция div— целочисленное деление. Делимое и делитель являются целыми числами, а результат — целая часть частного. Например: 7 div2 =3. Для отбрасывания младшего разряда целого числа используется целочисленное деление на 10. Например: 1234 div10 = 123 — отбрасывается младший разряд.
Операция modдает остаток от целочисленного деления. Например: 7 mod2 = 1. Для получения младшего разряда целого числа вычисляется остаток от целочисленного деления на 10. Например: 1234 mod10 = 4 — выделяется разряд единиц.
Пример.При переводе по данной программе двоичного числа 11012 в десятичную систему на экране увидим:
Следовательно, в итоге получили: 11012=13.
Для лучшего понимания работы программы внимательно изучите приведенную далее трассировочную таблицу. Она отражает изменения значений переменных на каждом шаге выполнения алгоритма, реализованного в программе.
| Шаг алгоритма | Команды алгоритма | N2 | k | N10 | Проверка условия |
| Ввод N2, k:=1, N10:=0 | |||||
| N200 | 1101≠0, да | ||||
| N10:=N10 + (N2 mod 10)*k | |||||
| k:=k*2 | |||||
| N2:=N2 div 10 | |||||
| N200 | 110≠0,да | ||||
| N10:=N10 + (N2 mod 10)*k | |||||
| k:=k*2 | |||||
| N2:=N2 div 10 | |||||
| N200 | 11≠0,да | ||||
| N10:=N10 + (N2 mod 10)*k | |||||
| k:=k*2 | |||||
| N2:=N2 div 10 | |||||
| N2<>0 | 1≠0,да | ||||
| N10:=N10 + (N2 mod 10)*k | |||||
| k:=k*2 | |||||
| N2:=N2 div 10 | |||||
| N200 | 0≠0, нет | ||||
| Вывод N10 |
Программа перевода десятичного числа в двоичную систему счисления
Теперь познакомьтесь с программой перевода целого десятичного числа в двоичную систему счисления.
Program Numbers_10_2;
var N10, N2, k: longint;
Begin
Repeat
until (N10=0);
Здесь использованы те же обозначения, что и в предыдущей программе. Исходными данными являются: N10 — десятичное число. Результат получается в переменной N2 — число в системе с основанием 2.
В алгоритме используется цикл с постусловием (repeat. until). Цикл повторяется до выполнения условия: N10 = 0.
Примериспользования программы. Переведем число 25 в двоичную систему счисления. Работа программы на экране компьютера отразится следующим образом:
Следовательно, в результате получили: 25 =110012.
Для лучшего понимания работы программы рекомендуем построить трассировочную таблицу, наподобие предыдущей.
Коротко о главном
Программирование перевода 10 → 2 и 2 → 10 основано на использовании операций над целыми числами: div — целочисленное деление, mod — остаток от целочисленного деления.
Вопросы и задания
1. Введите в компьютер и отладьте программу Number S_2_l 0. Переведите с ее помощью в десятичную систему счисления следующие двоичные числа: 111110; 1111111; 100000. Проверьте правильность результатов.
2. Введите в компьютер и отладьте программу Number s_l 0_2. Переведите с ее помощью в двоичную систему счисления следующие десятичные числа: 255; 512; 1023. Проверьте правильность результатов.
Сложность алгоритмов
Основные темы параграфа:
■ объемная сложность алгоритма;
■ временная сложность алгоритма;
■ сложность алгоритмов перебора.
Традиционно принято оценивать степень сложности алгоритма по объему используемых им основных ресурсов компьютера: процессорного времени и оперативной памяти. В связи с этим вводятся такие понятия, как временная сложность и объемная сложность алгоритма.
Объемная сложностьсвязана с количеством данных, которые при обработке нужно хранить в оперативной памяти. Проблемы могут возникнуть при обработке больших массивов данных (числовых или символьных). Если весь объем обрабатываемой информации не помещается одновременно в оперативную память, то эти данные приходится хранить на устройствах внешней памяти (дисках) и в процессе обработки перемещать частями из внешней памяти в оперативную память и обратно. Поскольку время чтения и записи данных на устройствах внешней памяти намного больше времени обмена процессора с оперативной памятью, то в целом время выполнения программы существенно возрастает.
Временная сложностьсвязана с количеством операций, выполняемых процессором в течение работы программы. Наибольшая часть процессорного времени тратится на выполнение циклов. Поэтому оценка временной сложности производится по количеству повторений циклов. Нетрудно понять, что при обработке массива данных количество повторений циклов связано с размером массива. Например, пусть вычисляется сумма элементов массива X, состоящего изN чисел:
S:=0;fori:=ltoN doS:=S + X[i];
Если вернуться к алгоритму поиска наибольшего и наименьшего значений массива, то в нем также имеется один цикл, хотя тело цикла содержит большее число операций. Но с увеличением размера массива (N) время выполнения программы будет также увеличиваться линейно, т. е. пропорционально N. Следовательно, временная сложность алгоритмов суммирования массива и поиска в массиве максимального (минимального) элемента одинаковая — линейная.
• вычислим среднюю длину внутреннего цикла:
• умножим эту величину на число повторений внешнего цикла:
Временная сложность алгоритма определяется слагаемым с наибольшей степенью: Т
N 2 . В таком случае говорят, что временная сложность алгоритма сортировки методом пузырька имеет второй порядок по объему данных, т. е. пропорциональна квадрату N. Например, если размер массива увеличить в 10 раз, то время сортировки возрастет в 100 раз.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.