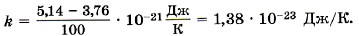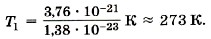на каком основании можно предполагать существование связи между температурой и кинетической энергией
§ 60. Определение температуры. Энергия теплового движения молекул (окончание)
Температура — мера средней кинетической энергии молекул
Из основного уравнения молекулярно-кинетической теории (9.8) и определения температуры (9.13) вытекает важнейшее следствие:
Важно
абсолютная температура есть мера средней кинетической энергии движения молекул.
Из уравнений (9.7) и (9.13) следует, что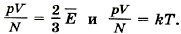 
Отсюда вытекает связь между средней кинетической энергией поступательного движения молекулы и температурой:
Важно
Средняя кинетическая энергия хаотичного поступательного движения молекул газа пропорциональна абсолютной температуре.
Чем выше температура, тем быстрее движутся молекулы. Таким образом, выдвинутая ранее догадка о связи температуры со средней скоростью молекул получила надёжное обоснование. Соотношение (9.16) между температурой и средней кинетической энергией поступательного движения молекул установлено для идеальных газов. Однако оно оказывается справедливым для любых веществ, у которых движение атомов или молекул подчиняется законам механики Ньютона. Оно верно для жидкостей, а также и для твёрдых тел, где атомы могут лишь колебаться возле положений равновесия в узлах кристаллической решётки. При приближении температуры к абсолютному нулю энергия теплового движения молекул приближается к нулю, т. е. прекращается поступательное тепловое движение молекул.
Обсудите с одноклассником, можно ли считать, что средняя кинетическая энергия теплового движения молекул — мера температуры.
Зависимость давления газа от концентрации его молекул и температуры. Учитывая, что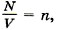 
из формулы (9.13) получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:
Выведите закон Авогадро, используя соотношение (9.17)
Из формулы (9.17) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же.
Отсюда следует закон Авогадро, известный вам из курса химии.
Закон Авогадро
В равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Ключевые слова для поиска информации по теме параграфа.
Абсолютная температура. Постоянная Больцмана. Закон Авогадро
Вопросы к параграфу
1. На каком основании можно предполагать существование связи между температурой и кинетической энергией молекул?
2. Как связаны объём, давление и число молекул различных газов в состоянии теплового равновесия?
3. Чему равен абсолютный нуль температуры по шкале Цельсия?
4. Какие преимущества имеет абсолютная шкала температур по сравнению со шкалой Цельсия?
5. Каков физический смысл постоянной Больцмана? Можно ли её определить теоретически, не обращаясь к эксперименту?
6. Как зависит от температуры средняя кинетическая энергия поступательного движения молекул газа?
7. Почему концентрация молекул всех газов одна и та же при одинаковых давлениях и температурах?
8. Как зависит средняя кинетическая энергия поступательного движения молекул от их массы?
Образцы заданий ЕГЭ
А 1. Температура газа в сосуде равна 2 °С. По абсолютной шкале температур это составляет
1) 136,5 К 2) 271 К 3) 275 К 4) 546 К
А 2. На рисунке показана часть шкалы комнатного термометра. Определите абсолютную температуру воздуха в комнате.
1) 22 °С 2) 18 °С 3) 295 К 4) 291 К
А 3. Как изменится средняя кинетическая энергия теплового движения одноатомного идеального газа при повышении его температуры в 2 раза?
1) увеличится в 4 раза 3) уменьшится в 2 раза
2) увеличится в 2 раза 4) уменьшится в 4 раза
А 4. В закрытом сосуде абсолютная температура идеального газа уменьшилась в 3 раза. При этом давление газа на стенки сосуда
1) увеличилось в 9 раз 3) уменьшилось в √3 раза
2) уменьшилось в 3 раза 4) не изменилось
§ 60. Определение температуры. Энергия теплового движения молекул (окончание)
Постоянная Больцмана. Определим коэффициент k в формуле (9.13) так, чтобы изменение температуры на один кельвин (1 К) было равно изменению температуры на один градус по шкале Цельсия (1 °С).
Мы знаем значения величины Θ при 0 °С и 100 °С (см. формулы (9.9) и (9.11)). Обозначим абсолютную температуру при 0 °С через Т1, а при 100 °С через Т2. Тогда согласно формуле (9.12)
называется постоянной Больцмана в честь Л. Больцмана, одного из основателей молекулярно-кинетической теории газов.
Важно
Постоянная Больцмана связывает температуру Θ в энергетических единицах с температурой Т в кельвинах.
Это одна из наиболее важных постоянных в молекулярно-кинетической теории.
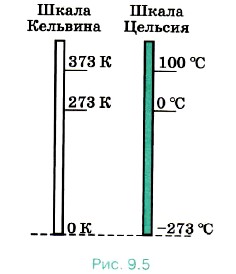
Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:
Важно
Изменение абсолютной температуры ΔТ равно изменению температуры по шкале Цельсия Δt: ΔТ(К) = Δt (°С).
Следует ли из фразы «Один кельвин и один градус шкалы Цельсия совпадают», что 27 °С = 27 К?
Отметим важнейший факт: абсолютный нуль температуры недостижим!
Температура — мера средней кинетической энергии молекул. Из основного уравнения молекулярно-кинетической теории (9.8) и определения температуры (9.13) вытекает важнейшее следствие:
Важно
абсолютная температура есть мера средней кинетической энергии движения молекул.
Из уравнений (9.7) и (9.13) следует, что 
Отсюда вытекает связь между средней кинетической энергией поступательного движения молекулы и температурой:
Важно
Средняя кинетическая энергия хаотичного поступательного движения молекул газа пропорциональна абсолютной температуре.
Чем выше температура, тем быстрее движутся молекулы. Таким образом, выдвинутая ранее догадка о связи температуры со средней скоростью молекул получила надёжное обоснование. Соотношение (9.16) между температурой и средней кинетической энергией поступательного движения молекул установлено для идеальных газов. Однако оно оказывается справедливым для любых веществ, у которых движение атомов или молекул подчиняется законам механики Ньютона. Оно верно для жидкостей, а также и для твёрдых тел, где атомы могут лишь колебаться возле положений равновесия в узлах кристаллической решётки. При приближении температуры к абсолютному нулю энергия теплового движения молекул приближается к нулю, т. е. прекращается поступательное тепловое движение молекул.
Обсудите с одноклассником, можно ли считать, что средняя кинетическая энергия теплового движения молекул — мера температуры.
Зависимость давления газа от концентрации его молекул и температуры. Учитывая, что 
из формулы (9.13) получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:
Выведите закон Авогадро, используя соотношение (9.17)
Из формулы (9.17) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же.
Отсюда следует закон Авогадро, известный вам из курса химии.
Закон Авогадро
В равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Ключевые слова для поиска информации по теме параграфа.
Абсолютная температура. Постоянная Больцмана. Закон Авогадро
Вопросы к параграфу
1. На каком основании можно предполагать существование связи между температурой и кинетической энергией молекул?
2. Как связаны объём, давление и число молекул различных газов в состоянии теплового равновесия?
3. Чему равен абсолютный нуль температуры по шкале Цельсия?
4. Какие преимущества имеет абсолютная шкала температур по сравнению со шкалой Цельсия?
5. Каков физический смысл постоянной Больцмана? Можно ли её определить теоретически, не обращаясь к эксперименту?
6. Как зависит от температуры средняя кинетическая энергия поступательного движения молекул газа?
7. Почему концентрация молекул всех газов одна и та же при одинаковых давлениях и температурах?
8. Как зависит средняя кинетическая энергия поступательного движения молекул от их массы?
Образцы заданий ЕГЭ
А1. Температура газа в сосуде равна 2 °С. По абсолютной шкале температур это составляет
1) 136,5 К 2) 271 К 3) 275 К 4) 546 К
А2. На рисунке показана часть шкалы комнатного термометра. Определите абсолютную температуру воздуха в комнате.
1) 22 °С 2) 18 °С 3) 295 К 4) 291 К
А3. Как изменится средняя кинетическая энергия теплового движения одноатомного идеального газа при повышении его температуры в 2 раза?
1) увеличится в 4 раза 3) уменьшится в 2 раза
2) увеличится в 2 раза 4) уменьшится в 4 раза
А4. В закрытом сосуде абсолютная температура идеального газа уменьшилась в 3 раза. При этом давление газа на стенки сосуда
§ 60. Определение температуры. Энергия теплового движения молекул (окончание)
Постоянная Больцмана. Определим коэффициент k в формуле (9.13) так, чтобы изменение температуры на один кельвин (1 К) было равно изменению температуры на один градус по шкале Цельсия (1 °С).
Мы знаем значения величины Θ при 0 °С и 100 °С (см. формулы (9.9) и (9.11)). Обозначим абсолютную температуру при 0 °С через Т1, а при 100 °С через Т2. Тогда согласно формуле (9.12)
называется постоянной Больцмана в честь Л. Больцмана, одного из основателей молекулярно-кинетической теории газов.
Важно
Постоянная Больцмана связывает температуру Θ в энергетических единицах с температурой Т в кельвинах.
Это одна из наиболее важных постоянных в молекулярно-кинетической теории.
Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:
Важно
Изменение абсолютной температуры ΔТ равно изменению температуры по шкале Цельсия Δt: ΔТ(К) = Δt (°С).
Следует ли из фразы «Один кельвин и один градус шкалы Цельсия совпадают», что 27 °С = 27 К?
Отметим важнейший факт: абсолютный нуль температуры недостижим!
Температура — мера средней кинетической энергии молекул. Из основного уравнения молекулярно-кинетической теории (9.8) и определения температуры (9.13) вытекает важнейшее следствие:
Важно
абсолютная температура есть мера средней кинетической энергии движения молекул.
Из уравнений (9.7) и (9.13) следует, что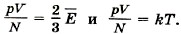 
Отсюда вытекает связь между средней кинетической энергией поступательного движения молекулы и температурой:
Важно
Средняя кинетическая энергия хаотичного поступательного движения молекул газа пропорциональна абсолютной температуре.
Чем выше температура, тем быстрее движутся молекулы. Таким образом, выдвинутая ранее догадка о связи температуры со средней скоростью молекул получила надёжное обоснование. Соотношение (9.16) между температурой и средней кинетической энергией поступательного движения молекул установлено для идеальных газов. Однако оно оказывается справедливым для любых веществ, у которых движение атомов или молекул подчиняется законам механики Ньютона. Оно верно для жидкостей, а также и для твёрдых тел, где атомы могут лишь колебаться возле положений равновесия в узлах кристаллической решётки. При приближении температуры к абсолютному нулю энергия теплового движения молекул приближается к нулю, т. е. прекращается поступательное тепловое движение молекул.
Обсудите с одноклассником, можно ли считать, что средняя кинетическая энергия теплового движения молекул — мера температуры.
Зависимость давления газа от концентрации его молекул и температуры. Учитывая, что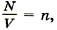 
из формулы (9.13) получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:
Выведите закон Авогадро, используя соотношение (9.17)
Из формулы (9.17) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же.
Отсюда следует закон Авогадро, известный вам из курса химии.
Закон Авогадро
В равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Ключевые слова для поиска информации по теме параграфа.
Абсолютная температура. Постоянная Больцмана. Закон Авогадро
Вопросы к параграфу
1. На каком основании можно предполагать существование связи между температурой и кинетической энергией молекул?
2. Как связаны объём, давление и число молекул различных газов в состоянии теплового равновесия?
3. Чему равен абсолютный нуль температуры по шкале Цельсия?
4. Какие преимущества имеет абсолютная шкала температур по сравнению со шкалой Цельсия?
5. Каков физический смысл постоянной Больцмана? Можно ли её определить теоретически, не обращаясь к эксперименту?
6. Как зависит от температуры средняя кинетическая энергия поступательного движения молекул газа?
7. Почему концентрация молекул всех газов одна и та же при одинаковых давлениях и температурах?
8. Как зависит средняя кинетическая энергия поступательного движения молекул от их массы?
Образцы заданий ЕГЭ
А1. Температура газа в сосуде равна 2 °С. По абсолютной шкале температур это составляет
1) 136,5 К 2) 271 К 3) 275 К 4) 546 К
А2. На рисунке показана часть шкалы комнатного термометра. Определите абсолютную температуру воздуха в комнате.
1) 22 °С 2) 18 °С 3) 295 К 4) 291 К
А3. Как изменится средняя кинетическая энергия теплового движения одноатомного идеального газа при повышении его температуры в 2 раза?
1) увеличится в 4 раза 3) уменьшится в 2 раза
2) увеличится в 2 раза 4) уменьшится в 4 раза
А4. В закрытом сосуде абсолютная температура идеального газа уменьшилась в 3 раза. При этом давление газа на стенки сосуда
Вопросы и ответы по теме МКТ
Ищем педагогов в команду «Инфоурок»
Какие факты позволяют судить о том, что газ оказывает давление на тела, с которыми он соприкасается?
Раздувающаяся во все стороны волейбольная камера; не выливающаяся вода из перевернутой сравнительно тонкой стеклянной трубки, запаянной с одного конца; газ расширяется под поршнем, с которого снята нагрузка.
Чтобы могло пояснить давление газа на стенки сосуда?
1. Газ, как и любое вещество, состоит из молекул;
2. Молекулы хаотично и беспрерывно движутся;
3. Молекулы взаимодействуют между собой.
Какие упрощения вводятся для расчета давления газа на стенки сосуда?
2.Сил взаимодействия между частицами нет и потенциальная энергия равна нулю;
3. Одинаковые усредненные скорости молекул;
4. Удары молекул о стенки сосуда абсолютно упругие.
Какой газ называется идеальным?
Идеальным газом называется газ, отвечающий следующим свойствам:
1. Молекулы газа находятся на достаточно большом расстоянии друг от друга;
2. Между частицами отсутствуют силы взаимодействия, следовательно, потенциальная энергия взаимодействия равна нулю.
Перечислите основные микроскопические параметры газа?
Энергия, масса и скорость движения молекул газа.
Что называется концентрацией?
Концентрацией называется физическая величина, измеряемая отношение числа частиц к объему, в котором они находятся.
Какова единица концентрации в СИ?
За единицу концентрации в СИ принята такая концентрация, при которой одна частица относится к одному кубическому метру объема, в котором она находится.
Каков физический смысл концентрации?
Концентрация показывает какую часть составляет число частиц в единице объема.
Зачем для расчета давления газа на стенки сосуда рассматривается понятие размерность?
Путем сопоставления размерностей можно установить характер зависимости, которая связывает величины, характеризующие давление газа на стенки сосуда.
От чего и как зависит давление газа на стенки сосуда?
Давление газа зависит от массы молекулы, ее скорости движения и от концентрации; а также давление газа прямо пропорционально концентрации молекул в сосуде и их средней кинетической энергии.
Как можно пояснить возникновение давления газа?
Возникновение давления газа можно пояснить с помощью простой механической модели, включающей диск и манометр. Дробинки играют роль молекул. В результате многочисленных ударов скатывающихся по наклонному желобу дробинок, на диск действует некоторая средняя сила давления.
Какое свойство газа связано с его давлением?
Свойство упругости связано с давлением газа: при сжатии газа увеличивается его давление.
Где используется сжатый газ?
Сжатый газ используется в компрессорах, вентиляторах, кессонах, пневматических отбойных молотках, амортизаторах; для пневмотранспортировки по трубам газов, заключенных в специальные капсулы.
К какому выводу пришел Джозеф Блэк, изучая тепловые явления?
Блэк сформировал мысль о необходимости различия между понятиями «теплота», «температура».
На каком основании можно предполагать существование связи между температурой и кинетической энергией молекул?
На основании экспериментально выявленного факта, при котором газы приходят в состояние теплового равновесия, можно предположить, что температура является мерой средней кинетической энергии и наоборот.
Каковы условия проведения опыта, который подтверждает существование связи между температурой и кинетической энергии молекул?
Три сосуда с кислородом, водородом и гелием помещают сначала в тающий лед, а затем в кипящую воду. Газы имеют разные объемы, разные давления. Число молекул в сосудах также различно.
Каков принцип проведения опыта по нахождению энергетического содержания градуса?
Нужно исходить из способа построения температурной шкалы Цельсия. Используются две опорные точки: 0 градусов Цельсия соответствует состоянию тающего льда, 100 градусов Цельсия- состояние кипящей воды. Средняя кинетическая энергия изменяется относительно ее предыдущего значения в 1,3661 раз. Т.о., если вычитать из большего значения этой величины меньшее и разделить полученное выражение на 100, то мы получим энергетическое содержание градуса.
Каково энергетическое содержание градуса?
Какова связь среднекинетической энергии молекул и температуры?
Средняя кинетическая энергия хаотичного поступательного движения молекул одноатомного идеального газа прямо пропорциональна его температуре.
Каков физический смысл постоянной Больцмана?
Постоянная Больцмана показывает какую часть от температуры составляет средняя кинетическая энергия.
Какого численное значение и единица постоянной Больцмана?
Что такое абсолютный нуль?
То, что температура не может быть как угодно малой, определяет одну опорную точку, которая носит абсолютный характер и называется абсолютным нулем.
Каков принцип построения шкалы Кельвина?
Берется шкала температур, у которой ноль является абсолютным нулем, с интервалами, равными интервалам в шкале Цельсия.
Каково соотношения между температурными шкалами Цельсия и Кельвина?
Каковы принципы построения температурных шкал Фаренгейта, Реомюра и Делиля?
Перечислите примеры использования термометров в различных областях деятельности человека.
Термометры используются для метеорологических и геофизических целей, для определения температуры плавления некоторых веществ.
Температура тела здорового человека 37˚С (если термометр оставить не подмышку, как это принято в нашей стране, а брать в рот, как это принято, например, в Америке). Чему равна температура тела здорового человека по шкалам Фаренгейта и Реомюра?
Перечислите макроскопические параметры газа?
Давление, объем и температура.
На каком основании мы можем предполагать, что макроскопические параметры газа взаимосвязаны?
На установленных экспериментальных фактах:
1. Перемещающийся столбик воды в открытом манометре при нагревании колбы с воздухом;
2. Слетающая капроновая крышка с банки, в которую подали искру с помощью электрофорной машины;
3. Пузырьки, выходящие из нагретого руками, а до этого охлажденного стеклянного шара с воздухом.
Каким уравнением устанавливается связь между давлением идеального газа и температурой?
Каким уравнением устанавливается связь между макроскопическими параметрами газа?
Что такое универсальная газовая постоянная и чему она равна?
Какие процессы называются изопроцессами?
Изопроцессами называются такие процессы, когда какой-либо параметр газа остается в процессе изменения его состояния постоянным.
Какой процесс называется изотермическим?
Изотермический процесс – процесс, при котором температура является постоянной величиной.
Какой процесс называется изохорическим?
Изохорический процесс – процесс, при котором объем является постоянной величиной.
Какой процесс называется изобарным?
Изобарный процесс – процесс, при котором давление является постоянной величиной
Как экспериментально подтверждается каждый газовый закон?
Изучить и проверить газовые законы можно с помощью специальных устройств: герметический гофрированный сосуд, соединенный с манометром (об объеме можно судить с помощью линейки, а температура регистрируется термометром) и устройство, включающее поршень, стеклянный цилиндр, манометр и термометр.
Какими свойствами обладают газы?
1. При нагревании объем газов увеличивается;
2. Хорошая сжимаемость, упругость;
3. Газы не имеют собственной формы, собственного объема, а принимают форму и занимают объем сосуда, в котором находятся;
4. Давление газов и их объем связаны друг с другом (если возрастает одна величина, то уменьшается другая).
Почему и при каких условиях все газы ведут себя одинаково?
Все газы ведут себя как идеальные при не слишком высоких давлениях и не слишком низких температурах. Газы обладают свойствами, которые не зависят от сил взаимодействия частиц между собой. Вот поэтому все газы ведут себя одинаково.
Приведите примеры использования свойств газов в различных областях жизни и деятельности человека?
В газовых термометрах, реактивном движении (ракете), барокамерах, доильной установке (вакуумный насос).
При переходе определенной массы газа из одного состояния в другое его давление уменьшается, а температура увеличивается. Как меняется его объем?
Согласно уравнению Менделеева-Клапейрона объем газа будет увеличиваться.
Вы надули щеки. Что при этом произойдет с объемом и давлением воздуха во рту? С каким законом это согласуется?
Объем и давление воздуха во рту увеличиваются. Температура не изменяется, значит это изотермический процесс, т.е. закон Бойля-Мариотта.