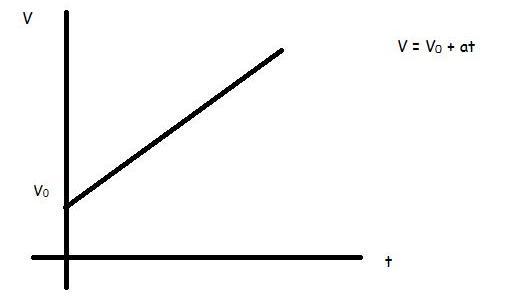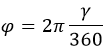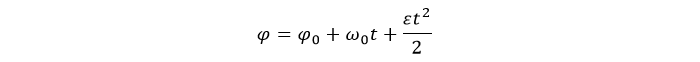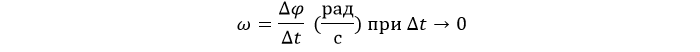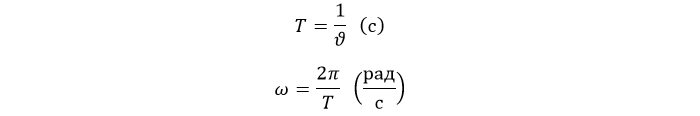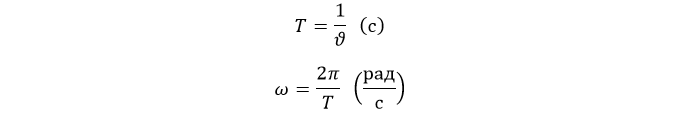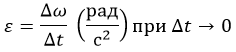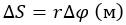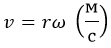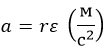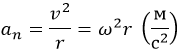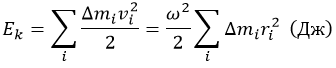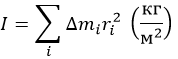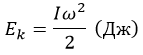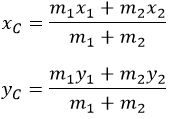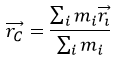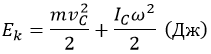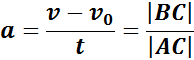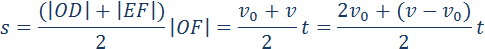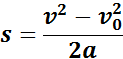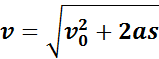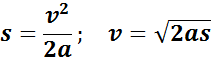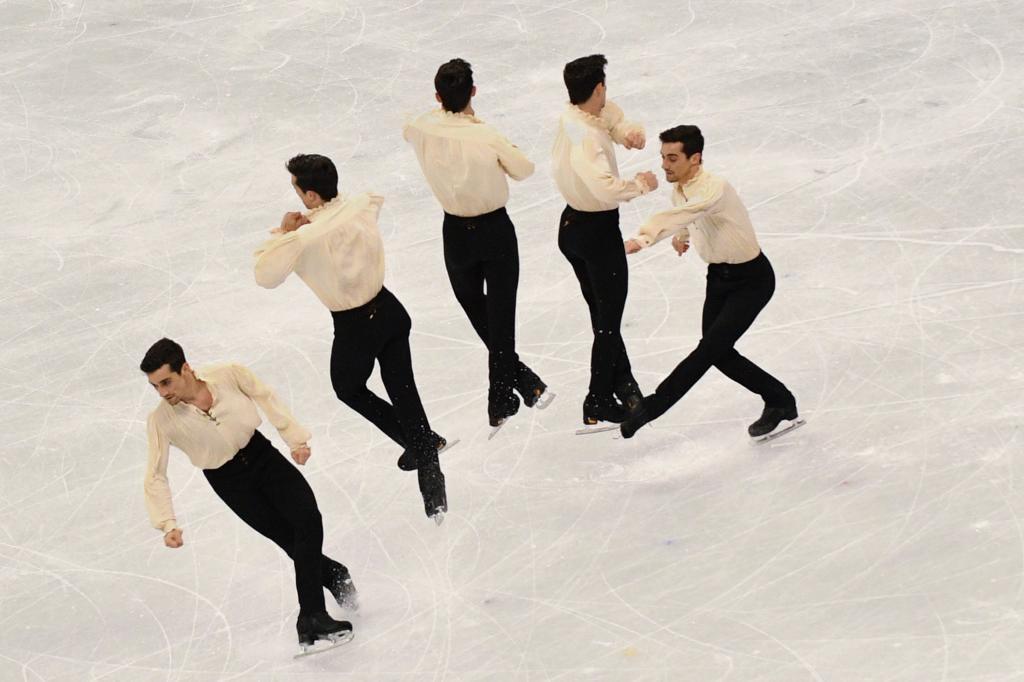какое вращение тела называют равноускоренным каковы его условия

Понятие о равноускоренном движении. Формулы перемещения и скорости. Равноускоренное вращение

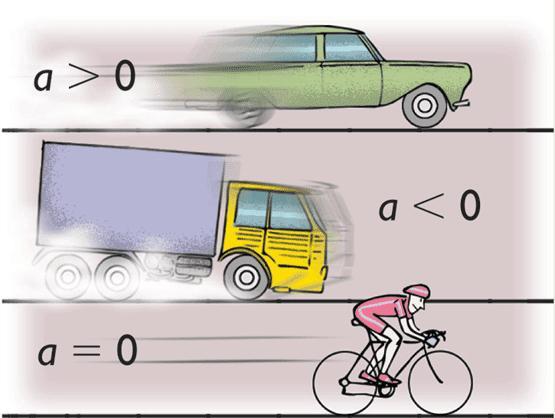
Движение с ускорением различных объектов окружает нас каждый день. Достаточно лишь вспомнить автомобили, самолеты, велосипеды, вращающиеся колеса и валы, чтобы понять всю важность ускоренного перемещения тел в жизни человека. Для описания этого движения в физике существует специальный раздел, он называется кинематикой. В данной статье рассмотрим, какими формулами описывается перемещение при равноускоренном движении.

Понятие об ускорении, скорости и пути

Вам будет интересно: «Тлетворный» — это о разложении

Прежде чем записывать формулы перемещения при равноускоренном движении, следует дать понятие основным величинам, которые в них фигурируют.

Начнем с пути. Под этой величиной понимают расстояние, которое проходит тело за интервал времени, двигаясь по известной траектории. Чем за более короткое время тело проходит некоторый путь L, тем больше его скорость. Таким образом, скоростью тела является быстрота преодоления им расстояний в пространстве. В данный момент времени расчет скорости выполняют по такой формуле:

Если наблюдать за телом, движущимся вдоль траектории некоторое время, и в каждой точке траектории измерять его скорость, то окажется, что она постоянно меняется. Изменение скорости характеризуют ускорением. В соответствии с определением ускорения оно вычисляется так:

Ускорение также является величиной векторной, только с направлением скорости оно не имеет ничего общего. Вектор ускорения повернут в сторону изменения скорости за данное время или, что одно и то же, в сторону действующей на тело силы.

Равноускоренное движение в физике

Чтобы понять, что такое равноускоренное перемещение, приведем следующий пример: предположим, что автомобиль находился в покое. Затем он начал движение, постоянно увеличивая свою скорость. Если за равные промежутки времени прирост модуля скорости автомобиля был одинаковым, то можно говорить о равноускоренном движении тела. Иными словами, во время рассматриваемого вида перемещения ускорение является величиной постоянной (a = const).

Не стоит думать, что движение с постоянным ускорением может только увеличивать скорость. В результате такого перемещения скорость тела может также уменьшаться до полной его остановки. Такая ситуация возникает, когда транспортное средство осуществляет процесс торможения. В этом случае ускорение будет направлено против вектора скорости.

В природе распространенным движением с постоянным ускорением является падение тел. До определенных скоростей, когда сопротивлением воздуха можно пренебречь, свободное падения является равноускоренным, причем величина ускорения равна 9,81 м/с2.

Изменение скорости при движении с постоянным ускорением

В отличие от ускорения, скорость при равноускоренном движении постоянной величиной не является. Рассмотрим для простоты перемещение по прямой линии. В случае если вектора величин a¯ и v¯ совпадают, имеет место следующая формула для скорости:

Это выражение предполагает, что до появления ускорения тело уже обладало некоторой скоростью v0.

Данная формула показывает, что скорость линейно возрастает с течением времени. График функции v(t) представляет собой прямую линию, которая пересекает ось y на расстоянии v0 от начала координат.

При равноускоренном движении скорость также может уменьшаться линейно. Для этого необходимо, чтобы вектора ускорения и скорости были противоположными (торможение автомобиля, свободный взлет тела в высоту). Для этого случая можно записать такое выражение:

Как и в предыдущем случае, графиком равенства является прямая, только коэффициент ее наклона к оси x будет не положительным, а отрицательным.

Перемещение при равноускоренном движении

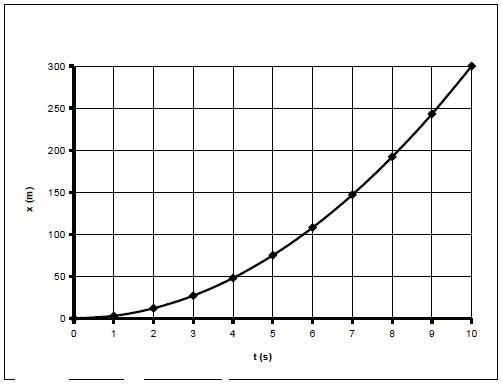
Формула пути однозначно получается, если взять интеграл по времени от скорости. В случае когда скорость тела увеличивается, для пути можно записать следующее выражение:

Видно, что графиком функции L(t) является парабола (ее правая ветвь). То есть пройденный путь с течением времени быстро увеличивается.

Если ускорение приводит к уменьшению скорости, тогда формула перемещения при равноускоренном движении примет вид:

Графиком для этого уравнения тоже будет парабола, однако ее ветвь постепенно приближается к некоторому постоянному значению. Последнее соответствует пройденному пути до остановки движущегося тела.

Движение с постоянным ускорением по окружности

Чтобы полнее охарактеризовать тему, следует также привести формулы перемещения при равноускоренном движении по окружности. В отличие от прямолинейного движения, этот вид перемещения описывается угловыми величинами. Тем не менее угловые величины являются полными аналогами соответствующих линейных характеристик.

Для скорости при равноускоренном движении вращения справедлива формула:

Аналогом пути для вращения является угол поворота θ. Для него справедлива формула:

Таким образом, при равноускоренном вращении формулы кинематики сохраняют свой вид, но в них стоят уже угловые физические величины.

Источник

Вращательное движение твердого тела – движение, при котором все точки объекта описывают траекторию в виде окружности.

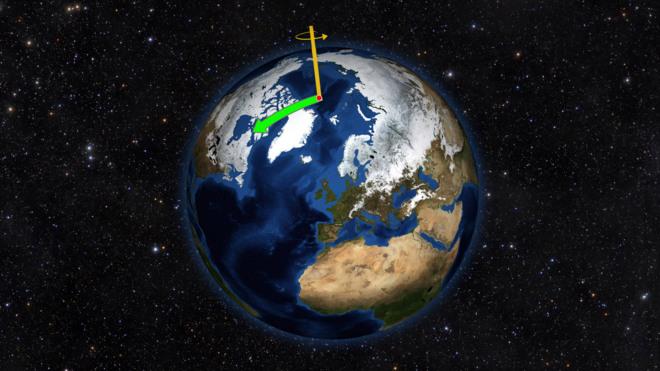
Распространенный случай в физике – вокруг покоящейся оси (рис. 1).

Рис. 1 Вращение твердого тела вокруг оси

Линия, соединяющая неподвижные точки, читается осью вращения. Кинематика перемещения в целом аналогична поступательной. Только путь измеряется не в метрах, а в радианах или градусах.

Последние связаны между собой следующей формулой:

ϕ – угол в радианах (рад);

γ – угол в градусах (°).

Закон и уравнение вращательного движения твердого тела

Законы движения также схожи. Для равноускоренного движения:

ϕ₀ – начальный угол (рад);

ω₀ – начальная угловая скорость (рад/с);

ε – угловое ускорение (рад/с 2 ).

Под положительным понимают перемещение против часовой стрелки.

Угловая скорость

В обычной жизни вращение оценивается в оборотах за единицу времени. За минуту чаще всего. Для расчетов такие характеристики неудобны. Поэтому определяется так:

Скорость в оборотах ν легко связать с угловой:

ν – скорость в оборотах (1/с).

Используется еще одна важная величина – период вращения T. За это время предмет совершает полный поворот:

Угловое ускорение

В уравнении движения был показан частный случай равноускоренного перемещения. Но это не всегда так. Также ε может принимать отрицательные значения в случае замедления.

Линейные величины

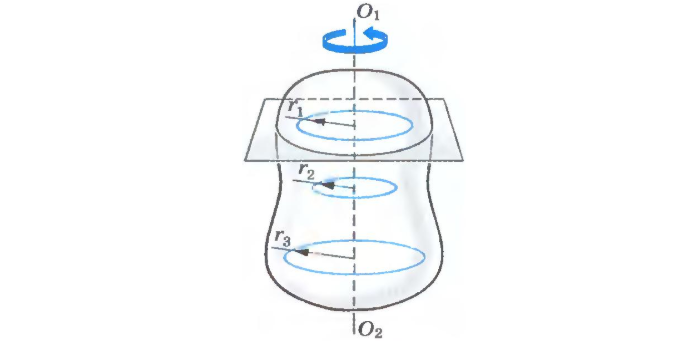
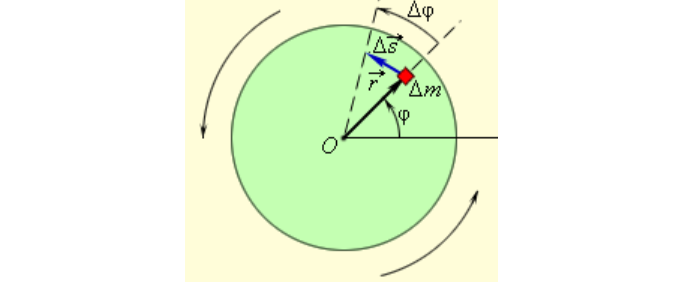
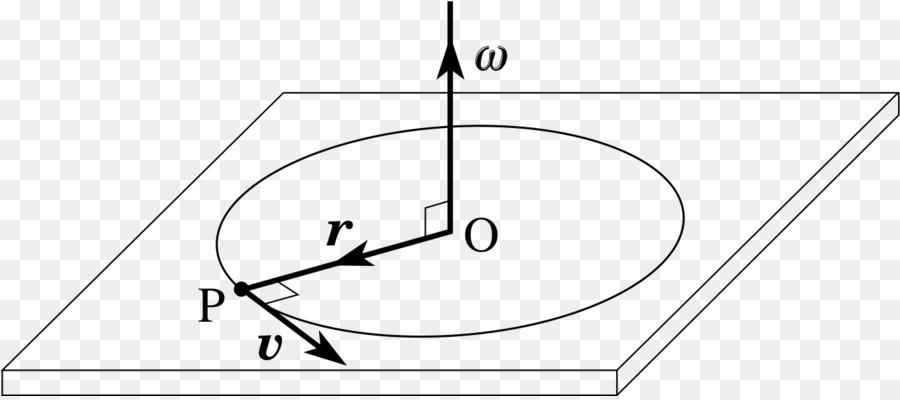
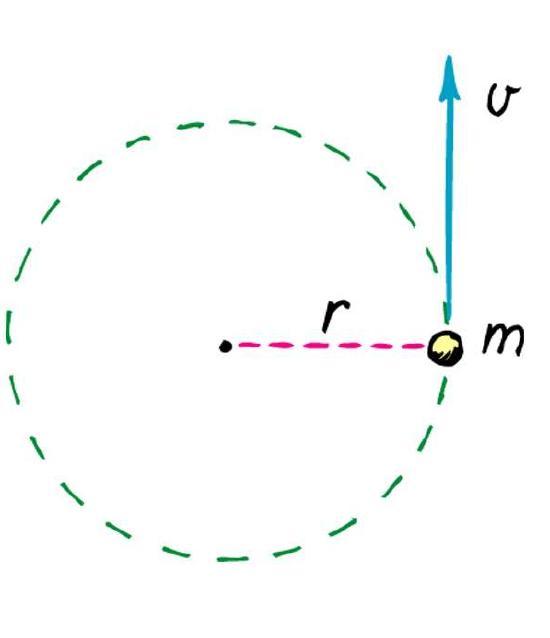
При малых величинах пройденный путь (см. рис. 2) будет равен:

где r – расстояние до центра вращения (м).

Откуда следует линейная скорость:

Вектор, перпендикулярный отрезку, r. То есть расположенный на касательной к окружности вращения.

И, соответственно, ускорение:

Кроме того, передвижение по кривой линии невозможно без центростремительного ускорения:

Возвратно-вращательное движение

Общий случай раскачивания маятника. Анализ подобных противоположных телодвижений пары объектов порождает некоторые парадоксы.

Возникают странные и дико звучащие названия вроде «безопорного движителя». Выводы в конечном итоге противоречат законам механики Ньютона.

Приверженцы таких рассуждений существуют и доводы имеют право на жизнь. Не все общепринятые взгляды безупречны. Евклидова геометрия тому пример. Теория довольно запутана, и здесь мы ее рассматривать не будем.

С учетом масс

Представив себе, что тело состоит из незначительных масс m_i, получим любопытные результаты. Кинетическая энергия выразится так:

Джоуль (Дж) – единица энергии и работы в системе СИ.

Моментом инерции относительно выбранной оси называется:

или в соответствующей интегральной форме.

Тогда энергия выразится следующим образом:

То есть имеется некий аналог массы. Но последняя является неизменной присущей объекту величиной. Момент же инерции зависит от местонахождения оси.

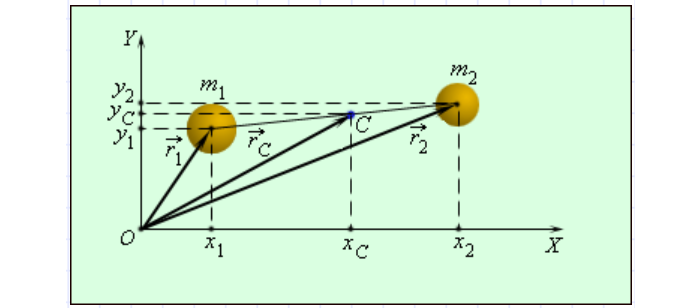
В реальных условиях распространен случай вращения вокруг оси, включающей центр масс. Найдем его для системы, указанной на рис. 3.

Рис. 3 Определение центра масс.

Определится по формулам:

Вектор, направленный из начала координат в центр масс, в общем случае выразится следующим образом:

Можно перевести в интегральную форму. В присутствии гравитации – заодно и центр тяжести.

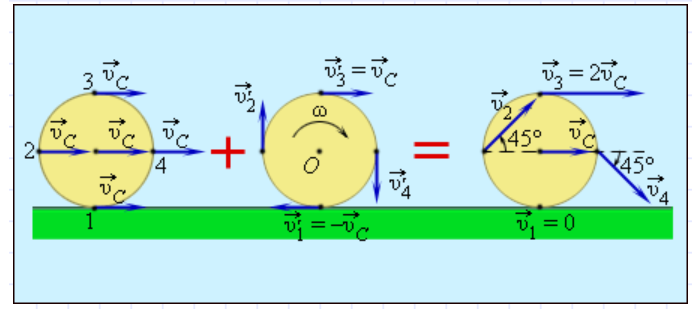
Можно сказать, что общее движение предмета включает поступательное и вращательное. Пример – качение чего-то округлого (рис. 4). При этом все перемещение точек можно исчерпывающе изобразить на рисунке. В таком варианте движение называется плоским.

Полная кинетическая энергия равна:

I_C – момент инерции относительно оси, включающей центр масс.

Рис. 4 Качение колеса

Частные случаи вращательного движения

1. Равномерное (рис. 5), с постоянной скоростью, с нулевым ускорением.

Выражается уравнением: φ = φ₀ + ωt

2. Равноускоренное. Рассмотрено ранее. Но все же уместны некоторые пояснения (рис. 6).

3. Вокруг неподвижной оси. Наиболее распространенный в рассмотрении вариант. Как для реальных нужд, так и в теории.

4. Возвратно-вращательное. В математическом выражении напоминает колебания. При подробном рассмотрении вызывает неудобные вопросы.

Заключение

Для разработчиков оборудования тема отнюдь не праздная. Рассматриваются задачи по передаче силового момента (в частности в ременных механизмах). Разбирается механика работы подшипников, гироскопов.

В артиллерии снаряды стабилизируются вращением. Да и расчеты их на прочность связаны со сложным напряженным состоянием в связи с раскручиванием в стволе.

Орбиты планет имеют отношение к рассматриваемой кинематике.

На самом деле все сферы использования данной темы невозможно перечислить, это действительно нужный раздел.

Источник

Двойкам нет

Вращательным движением тела вокруг фиксированной оси называют движение, при котором произвольная точка тела, кроме тех, что лежат на оси вращения, движется по окружности в плоскости, перпендикулярной оси вращения, с центром, лежащим на этой оси.

Равноускоренное вращательное движение — это движение по окружности, при котором угловая скорость тела за каждые равные отрезки времени изменяется на одно и тоже значение.

Угловое ускорение — это физическая величина, которая характеризует быстроту изменения угловой скорости тела, которая равна первой производной от угловой скорости по времени: при вращении против часовой стрелки.

Скорость тела при равноускоренном вращении меняется не только по направлению, но и по модулю.

Нормальное ускорение — ускорение, которое характеризует изменение скорости по направлению, которое направлено по радиусу к центру окружности перпендикулярно касательной.

Тангенциальное ускорение — ускорение, которое характеризует изменение модуля скорости, направленное по касательной.

Модуль тангенциального ускорения определяется отношением изменения модуля скорости к промежутку времени, за которое это изменение произошло, т. е.

Модуль полного ускорения точки, которое направлено по се- кущей в сторону вогнутости траектории, определяется с помощью теоремы Пифагора:

Силу, действующую на тело при равноускоренном вращении, можно представить в виде суммы двух составляющих: тангенци- альной и нормальной, т. е. соответственно.

Линия действия силы — линия, вдоль которой происходит действие силы.

Плечо силы — это расстояние от оси вращения до линии действия силы.

Момент силы относительно оси — это скалярная величина, ко- торая является характеристикой вращательного действия силы, равная произведению модуля силы, действующей на твердое тело, на плечо силы этой силы относительно данной оси:
M = Fd.
Момент силы, которая вызывает вращение тела вокруг данной оси по часовой стрелке, является отрицательным, а момент силы, вращающей тело против часовой стрелки, — положительным.

Момент инерции тела относительно оси — это физическая величина, которая является мерой инертности тела во вращательном движении вокруг этой оси, равна сумме произведений масс всех частиц тела на квадраты их расстояний.

Теорема Штейнера: момент инерции тела относительно произвольной оси равен сумме моментов инерции этого тела относи- тельно оси, параллельной оси и проходящей через центр инерции, и произведения массы тела на квадрат расстояния между осями.

Источник

Равноускоренное движение

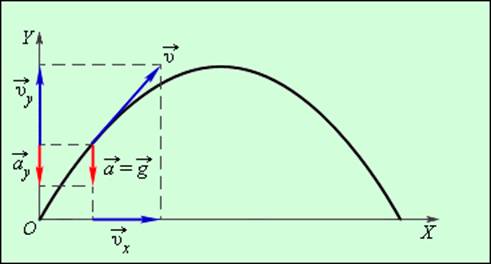
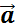
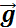
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения . Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY, была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX (рис. 1.4.1).

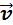
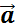
Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости и ускорения направлены вдоль прямой движения. Поэтому скорость υ и ускорение a в проекциях на направление движения можно рассматривать как алгебраические величины.

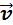
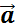
Проекции векторов скорости и ускорения на координатные оси. ax = 0, ay = –g

При равноускоренном прямолинейном движении скорость тела определяется формулой

(*)

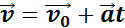
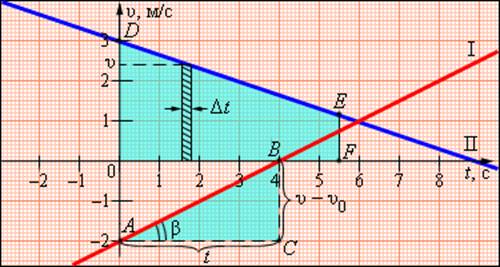
В этой формуле υ₀ – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.4.2).

Графики скорости равноускоренного движения

По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.4.2 для графика I. Ускорение численно равно отношению сторон треугольника ABC:

Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.

Для графика II: υ₀ = 3 м/с, a = –1/3 м/с 2

График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.

Так как υ – υ₀ = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:

(**)

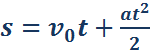
Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y₀ прибавить перемещение за время t:

(***)

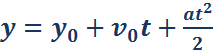
Это выражение называют законом равноускоренного движения.

При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ₀ и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде

Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ₀, ускорение a и перемещение s:

Если начальная скорость υ₀ равна нулю, эти формулы принимают вид

Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ₀, υ, s, a, y₀ являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.

Источник

Вращательное движение твердого тела: уравнение, формулы

В природе и технике мы часто сталкиваемся с проявлением вращательного движения твердых тел, например, валов и шестерен. Как в физике описывают этот тип движения, какие формулы и уравнения для этого применяются, эти и другие вопросы освещаются в данной статье.

Что такое вращение?

Вам будет интересно: Афронт — это ситуация, в которой не хочется оказаться

Чтобы вращение происходило, должно существовать центростремительное ускорение, которое возникает за счет центростремительной силы. Эта сила направлена от центра масс тела к оси вращения. Природа центростремительной силы может быть самой разной. Так, в космическом масштабе ее роль выполняет гравитация, если тело закреплено нитью, то сила натяжения последней будет центростремительной. Когда тело вращается вокруг собственной оси, роль центростремительной силы играет внутреннее электрохимическое взаимодействие между составляющими тело элементами (молекулами, атомами).

Вам будет интересно: Декабрист Оболенский Евгений Петрович: биография. Декабристские организации

Необходимо понимать, что без присутствия центростремительной силы тело будет двигаться прямолинейно.

Описывающие вращение физические величины

Во-первых, это динамические характеристики. К ним относятся:

Во-вторых, это кинематические характеристики. Перечислим их:

Кратко опишем каждую из названных величин.

Момент импульса определяется по формуле:

Момент инерции материальной точки рассчитывается с помощью выражения:

Для любого тела сложной формы величина I рассчитывается, как интегральная сумма моментов инерции материальных точек.

Момент силы M вычисляется так:

Физический смысл всех величин, в названии которых присутствует слово «момент», аналогично смыслу соответствующих линейных величин. Например, момент силы показывает возможность приложенной силы сообщить угловое ускорение системе вращающихся тел.

Кинематические характеристики математически определяются следующими формулами:

Как видно из этих выражений, угловые характеристики аналогичны по своему смыслу линейным (скорости v и ускорению a), только они применимы для круговой траектории.

Динамика вращения

В физике изучение вращательного движения твердого тела осуществляется с помощью двух разделов механики: динамики и кинематики. Начнем с динамики.

Динамика изучает внешние силы, действующие на систему вращающихся тел. Сразу запишем уравнение вращательного движения твердого тела, а затем, разберем его составные части. Итак, это уравнение имеет вид:

Момент силы, который действует на систему, обладающую моментом инерции I, вызывает появление углового ускорения α. Чем меньше величина I, тем легче с помощью определенного момента M раскрутить систему до больших скоростей за малые промежутки времени. Например, металлический стержень легче вращать вдоль его оси, чем перпендикулярно ей. Однако, тот же стержень легче вращать вокруг оси, перпендикулярной ему, и проходящей через центр масс, чем через его конец.

Закон сохранения величины L

Выше была введена эта величина, она называется моментом импульса. Уравнение вращательного движения твердого тела, представленное в предыдущем пункте, часто записывают в иной форме:

Если момент внешних сил M действует на систему в течение времени dt, то он вызывает изменение момента импульса системы на величину dL. Соответственно, если момент сил равен нулю, тогда L = const. Это и есть закон сохранения величины L. Для нее, используя связь между линейной и угловой скоростью, можно записать:

Таким образом, при отсутствии момента сил произведение угловой скорости и момента инерции является постоянной величиной. Этот физический закон используют фигуристы в своих выступлениях или искусственные спутники, которые необходимо повернуть вокруг собственной оси в открытом космосе.

Центростремительное ускорение

Выше, при изучении вращательного движения твердого тела, уже была описана эта величина. Также была отмечена природа центростремительных сил. Здесь лишь дополним эту информацию и приведем соответствующие формулы для расчета этого ускорения. Обозначим его ac.

Поскольку центростремительная сила направлена перпендикулярно оси и проходит через нее, то момента она не создает. То есть эта сила не оказывает совершенно никакого влияния на кинематические характеристики вращения. Тем не менее, она создает центростремительное ускорение. Приведем две формулы для его определения:

Таким образом, чем больше угловая скорость и радиус, тем большую силу следует приложить, чтобы удержать тело на круговой траектории. Ярким примером этого физического процесса является занос автомобиля во время поворота. Занос возникает, если центростремительная сила, роль которой играет сила трения, становится меньше, чем центробежная сила (инерционная характеристика).

Кинематика вращения

Три основные кинематические характеристики были перечислены выше в статье. Кинематика вращательного движения твердого тела формулами следующими описывается:

θ = ω*t => ω = const., α = 0;

θ = ω0*t + α*t2/2 => ω = ω0 + α*t, α = const.

В первой строке приведены формулы для равномерного вращения, которое предполагает отсутствие внешнего момента сил, действующего на систему. Во второй строке записаны формулы для равноускоренного движения по окружности.

Отметим, что вращение может происходить не только с положительным ускорением, но и с отрицательным. В этом случае в формулах второй строки следует перед вторым слагаемым поставить знак минус.

Пример решения задачи

На металлический вал в течение 10 секунд действовал момент силы 1000 Н*м. Зная, что момент инерции вала равен 50 кг*м2, необходимо определить угловую скорость, которую придал валу упомянутый момент силы.

Применяя основное уравнение вращения, вычислим ускорение вала:

Поскольку это угловое ускорение действовало на вал в течение времени t = 10 секунд, то для вычисления угловой скорости применяем формулу равноускоренного движения:

Здесь ω0 = 0 (вал не вращался до действия момента сил M).

Подставляем в равенство численные значения величин, получаем:

ω = 1000/50*10 = 200 рад/с.

Чтобы это число перевести в привычные обороты в секунду, необходимо его поделить на 2*pi. Выполнив это действие, получаем, что вал будет вращаться с частотой 31,8 об./с.

Источник