какое тело вращения не имеет образующей
Тест по теме «Тела вращения».
Ищем педагогов в команду «Инфоурок»
Тест по теме: «Тела вращения»
1. Какое тело вращения имеет 2 основания?
а) конус б) шар в) цилиндр
2. Какое тело вращения имеет в сечении треугольник?
а) конус б) шар в) цилиндр
3. Какое тело вращения не имеет образующей?
а) конус б) шар в) цилиндр.
4. Какая фигура является осевым сечением усеченного конуса?
а) круг б) треугольник в) трапеция.
5. Какая фигура является сечением шара?
а) прямоугольник б) круг в) ромб.
6. Какой элемент, не принадлежит цилиндру?
а) образующая б) апофема в) радиус
7. Найдите радиус конуса, если его образующая 13 дм, а высота 12 дм.
а) 25 дм б) 5 дм в) дм.
8. Найдите образующую усеченного конуса, если его радиусы 5 см и 10 см, а высота 4 см
а) см б) 19 см в) 9 см.
9. Найти высоту цилиндра, если диагональ его осевое сечение 15 м, а радиус 5 м
10. Найти площадь сечения шара, радиус которого 29 см, а плоскость сечения удалена от центра шара на 19 см
а) 551π см 2 б) см 2 в) 480π см 2
Тест по теме: «Тела вращения»
1. Какое тело вращения имеет 1 основание?
а) конус б) шар в) цилиндр
2. Какое тело вращения имеет в сечении прямоугольник?
а) конус б) шар в) цилиндр.
3. Какое тело вращения не имеет высоты?
а) конус б) шар в) цилиндр.
4. Какая фигура является осевым сечением шара?
а) круг б) треугольник в) трапеция.
5. Какую фигуру можно вращать вокруг своей стороны, чтобы получить конус?
а) равносторонний б) остроугольный в) прямоугольный
треугольник треугольник треугольник
6. Какой элемент, не принадлежит конусу?
а) высота б) ось в) медиана
7. Найти образующую конуса, если его радиус 4см, а высота 3см.
8. Найдите высоту усеченного конуса, если радиусы его оснований равны 5см и 8см, а образующая 11см.
9. Найти диагональ осевого сечения цилиндра, если его радиус 6 дм, а высота 8 дм
а) 10 дм б) дм в) 14дм
10. Найти площадь сечения шара, радиус которого 39 см, а плоскость сечения удалена от центра шара на 11см
а) 1400π см 2 б) см 2 в) 140π см 2
ОТВЕТЫ к тесту «Тела вращения»
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-830123
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
В Воронежской области ввели масочный режим в школах
Время чтения: 2 минуты
Вузам Москвы и Подмосковья рекомендовали с 8 ноября ввести смешанный формат обучения
Время чтения: 1 минута
В Минпросвещения предложили приравнять нападения на школы к терактам
Время чтения: 1 минута
СК предложил обучать педагогов выявлять деструктивное поведение учащихся
Время чтения: 1 минута
Кабмин утвердил список вузов, в которых можно получить второе высшее образование бесплатно
Время чтения: 2 минуты
В Башкирии школьные каникулы продлили до 14 ноября
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Помогите пожалуйста с тестом по математике 21 вопрос с вариантами ответов
Вопрос 1
Тело, состоящее из двух кругов и всех отрезков, соединяющих точки кругов называется:
Вопрос 2
Область определения функции –
a.
Это те аргументы, которые может принимать переменная
b.
Это те аргументы, которые может принимать значение
c.
Это те значения, которые может принимать независимая переменная
d.
Это те значения, которые может принимать аргумент
Вопрос 3
Какое тело вращения не имеет образующей?
Вопрос 4
Найти высоту цилиндра, если диагональ его осевое сечение 15 м, а радиус 5 м
Вопрос 5
Назовите формулу, раскрывающую геометрический смысл производной
Вопрос 6
Найдите периметр равнобедренного треугольника АВС, у которого АВ = ВС, если АВ = 12, АС = 6.
Вопрос 7
Вычислите ((х-1)5)’
Вопрос 8
Что не относится к основные элементарным телам вращения?
Вопрос 9
Вычислите (6х3)’
Вопрос 10
Найдите радиус конуса, если его образующая 13 дм, а высота 12 дм
Вопрос 11
Выполнен
Баллов: 0,00 из 1,00
Не отмеченоОтметить вопрос
Текст вопроса
К правильным многогранникам не относится:
Вопрос 14
Если в основании призмы лежит параллелограмм, то она является:
Вопрос 15
Площадь боковой поверхности усечённого конуса?
d.
Sбок= (r+R)*l
Вопрос 16
Какое тело вращения имеет 2 основания?
Вопрос 17
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани называется:
d.
Осью
Вопрос 18
Укажите область определения функции: y=arcsin 2x
Вопрос 20
Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется:
Вопрос 21
Грани параллелепипеда не имеющие общих вершин, называются:
Итоговая работа Многогранники и круглые тела
Зачётная тестовая работа по
теме « Многогранники и круглые тела »
2) Сколько боковых рёбер имеет прямоугольный параллелепипед?
7) Цилиндром называется тело, ограниченное поверхностью:
а) конической; б) концентрической; в) цилиндрической; г) сферической.
8) Осевым сечением конуса является:
а) треугольник; б) круг; в) прямоугольник; г) трапеция.
9) Боковая поверхность цилиндра определяется по формуле:
10) Сфера является поверхностью:
а) конуса; б) усеченного конуса; в) цилиндра; г) шара.
 |  |  |
 |  |
2) Объём прямоугольного параллелепипеда вычисляется по формуле:
3) Площадь полной поверхности куба вычисляется по формуле:
а ) S= 4 a ; б ) S = abc ; в ) S = 2(ab+bc+ac) ; г )S =6 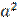
4) Какая фигура является диагональным сечением прямоугольного параллелепипеда?
а) трапеция ; б) прямоугольник ; в) треугольник ;г) параллелограмм.
5) Укажите верные утверждения :
а)объём пирамиды равен произведению площади основания на высоту;
б) равные тела имеют равные объёмы;
в) у призмы основания лежат в параллельных плоскостях ;
г) усечённая пирамида имеет одно основание.
6) Выберите верное утверждение:
а) длина образующей цилиндра называется радиусом цилин дра;
б) цилиндрическая поверхность называется боковой поверхностью цилиндра;
в) сечение цилиндра, перпендикулярное оси цилиндра, называется осевым;
г) цилиндр может быть получен в результате вращения треугольника
вокруг одной из сторон.
7) Конус может быть получен вращением:
а) прямоугольника вокруг одной из сторон;
б) равностороннего треугольника вокруг медианы;
в) прямоугольного треугольника вокруг одного из катетов;
г) равнобедренного треугольника вокруг высоты.
2) Найдите полную поверхность правильной четырёхугольной призмы по стороне основания 5 см и боковому ребру 6 см.
3) Цилиндр образован вращением прямоугольника с диагональю 5 см вокруг стороны длиной 3 см. Найдите: а)объем цилиндра ;б) площадь его полной поверхности
Тест по теме: «Тела вращения»
1. Какое тело вращения имеет 2 основания?
а) конус б) шар в) цилиндр
2. Какое тело вращения имеет в сечении треугольник?
а) конус б) шар в) цилиндр
3. Какое тело вращения не имеет образующей?
а) конус б) шар в) цилиндр.
4. Какая фигура является осевым сечением усеченного конуса?
а) круг б) треугольник в) трапеция.
5. Какая фигура является сечением шара?
а) прямоугольник б) круг в) ромб.
6. Какой элемент, не принадлежит цилиндру?
а) образующая б) апофема в) радиус
7. Найдите радиус конуса, если его образующая 13 дм, а высота 12 дм.
а) 25 дм б) 5 дм в) дм.
8. Найдите образующую усеченного конуса, если его радиусы 5 см и 10 см, а высота 4 см
а) см б) 19 см в) 9 см.
9. Найти высоту цилиндра, если диагональ его осевое сечение 15 м, а радиус 5 м
10. Найти площадь сечения шара, радиус которого 29 см, а плоскость сечения удалена от центра шара на 19 см
а) 551π см 2 б) см 2 в) 480π см 2
Зачётная тестовая работа по
теме « Многогранники и круглые тела »
1) Сколько диагоналей у прямоугольного параллелепипеда?
7) Конусом называется тело, ограниченное поверхностью:
а) конической; б) концентрической; в) цилиндрической; г) сферической.
8) Осевым сечением цилиндра является:
а) треугольник; б) круг; в) прямоугольник; г) трапеция.
9) Боковая поверхность конуса определяется по формуле:
10)Какая фигура получится при пересечении шара плоскостью?
а) сфера ; б) окружность ; в) круг ; г) цилиндр.
 |  |  |  |  |
2) Объём куба вычисляется по формуле:
а) V = 6 a 2 ; б) V = abc ; в) V = a 3 ; г) V = a 2
3)Площадь полной поверхности прямоугольного параллелепипеда вычисляется по формуле:
а ) S= a+b+c; б ) S = abc ; в ) S= 2(ab+bc+ac) ; г ) S = a 3
4) Апофема –высота боковой грани у многогранника:
а) куба ; б) параллелепипеда ; в) призмы ; г) пирамиды.
5) Укажите неверные утверждения :
а)объём пирамиды равен произведению площади основания на высоту;
б) равные тела имеют равные объёмы;
в) у призмы основания лежат в параллельных плоскостях ;
г) усечённая пирамида имеет одно основание.
6) Выберите верное утверждение:
а) радиус цилиндра не может равняться высоте цилиндра;
б) площадь боковой поверхности цилиндра равна произведению площади основания цилиндра на его высоту;
в) сечение цилиндра, параллельное оси цилиндра, называется осевым;
г) цилиндр может быть получен в результате вращения прямоугольника вокруг одной из его сторон.
7) Конус может быть получен вращением:
а) равностороннего треугольника вокруг медианы;
б) равнобедренного треугольника вокруг высоты;
в) прямоугольного треугольника вокруг одного из катетов;
г) прямоугольника вокруг одной из сторон.
1)Найдите диагонали прямоугольного параллелепипеда по трём его измерениям: 1;2;2.
2) Найдите полную поверхность правильной четырёхугольной призмы по стороне основания 6 см и боковому ребру 5 см.
3)Прямоугольный треугольник с гипотенузой 13 см вращается вокруг оси, содержащей катет длиной 5 см. Найти
а) объем полученного конуса;
б) площадь его полной поверхности.
Тест по теме: «Тела вращения»
1. Какое тело вращения имеет 1 основание?
а) конус б) шар в) цилиндр
2. Какое тело вращения имеет в сечении прямоугольник?
а) конус б) шар в) цилиндр.
3. Какое тело вращения не имеет высоты?
а) конус б) шар в) цилиндр.
4. Какая фигура является осевым сечением шара?
а) круг б) треугольник в) трапеция.
5. Какую фигуру можно вращать вокруг своей стороны, чтобы получить конус?
а) равносторонний б) остроугольный в) прямоугольный треугольник
6. Какой элемент, не принадлежит конусу?
а) высота б) ось в) медиана
7. Найти образующую конуса, если его радиус 4см, а высота 3см.
8. Найдите высоту усеченного конуса, если радиусы его оснований равны 5см и 8см, а образующая 11см.
9. Найти диагональ осевого сечения цилиндра, если его радиус 6 дм, а высота 8 дм
а) 10 дм б) дм в) 14дм
10. Найти площадь сечения шара, радиус которого 39 см, а плоскость сечения удалена от центра шара на 11см
Конспекты по математике на тему «Тела вращения. Объемы тел вращения»
Ищем педагогов в команду «Инфоурок»
Конспекты занятий по математике для студентов первого курса теме «Тела вращения. Объемы тел вращения».
Тела вращения — объёмные тела, полученные при вращении плоской фигуры вокруг своей оси или стороны.
Примеры тел вращения: цилиндр, конус, шар, сфера.
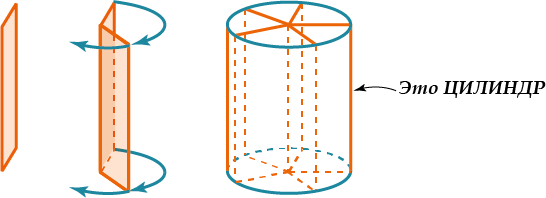
Цили́ндр (от греч. kýlindros, валик, каток) — геометрическое тело, образованное вращением прямоугольника вокруг одной из сторон.
Примеры тел, имеющих цилиндрическую форму: часть водопроводной трубы, консервная банка.
Радиусом цилиндра называется радиус его основания.
Высотой цилиндра называется расстояние между его основаниями.
Осью цилиндра называется прямая, проходящая через центр оснований, параллельно образующим.
Осевое сечение – сечение цилиндра плоскостью, проходящей через его ось.
Поверхность цилиндра состоит из оснований и боковой поверхности.
Боковая поверхность составлена из образующих.
Основания цилиндра равны и параллельны.
Образующие цилиндра равны и параллельны.
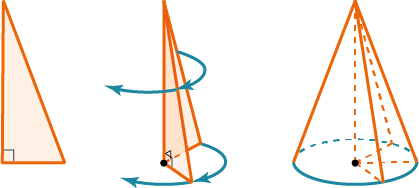
Ко́нус — тело вращения, образованное вращением прямоугольного треугольника, вокруг одного из его катетов.
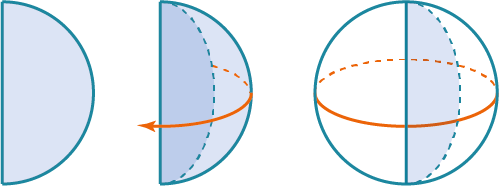
Шар — тело вращения, полученное вращением полукруга около его неподвижного диаметра.
Примеры тел, имеющих форму шара или сферы: мыльный пузырь, земля, футбольный и теннисный мячи.
Сфера это поверхность шара .
Концы любого диаметра называются диаметрально противоположными точками шара.
Плоскость, проходящая через центр шара, называется диаметральной плоскостью.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
1. Уравнение шара с радиусом R и центром в начале декартовой системе координат :
x 2 + y 2 + z 2 ≤ R 2
2. Уравнение шара с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0 ) в декартовой системе координат :
Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :
x 2 + y 2 + z 2 = R 2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0 ) в декартовой системе координат :
Формулы объема цилиндра, конуса и шара.
Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
3. Объем усеченного конуса.
Усеченный конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.
Тела вращения и их сечения
Телом вращения называется тело, образованное в результате вращения какой-либо линии вокруг прямой.
Примеры тел вращения.
Шар − образован полукругом, вращающимся вокруг диаметра разреза.
Цилиндр − образован прямоугольником, вращающимся вокруг одной из сторон.
Конус − образован прямоугольным треугольником, вращающимся вокруг одного из катетов.
При пересечении тела вращения плоскостью получается плоская фигура, ограниченная в большинстве случаев кривой линией. В частных случаях фигурой сечения может быть прямоугольник (для цилиндра) и треугольник (для конуса).
Осевым сечением цилиндра называется сечение плоскостью, проходящей через ось цилиндра. Осевое сечение цилиндра – прямоугольник, две стороны которого – образующие цилиндра, а две другие стороны – диаметры оснований цилиндра.
Секущая плоскость, перпендикулярная оси цилиндра, пересекает его по кругу.
Если плоскость проходит через высоту конуса FO, то сечение конуса этой плоскостью называют осевым и оно представляет собой равнобедренный треугольник, основанием которого является диаметр основания конуса, а боковыми сторонами – образующие конуса.
Сечение поверхности цилиндра
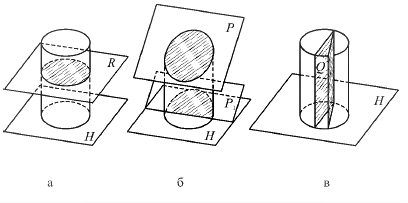
Бывают следующие случаи сечения поверхности прямого кругового цилиндра плоскостью:
1) окружность, если секущая плоскость Р перпендикулярна оси цилиндра, причем она параллельна основанию цилиндра;
2) эллипс, если секущая плоскость Р не перпендикулярна и не параллельна оси цилиндра;
3) пара прямых, если секущая плоскость Q содержит ось цилиндра или параллельна ей.
Рис. 104. Возможные случаи сечения поверхности цилиндра плоскостью: а – окружность; б – эллипс; в – пара прямых
Сечение поверхности конуса
В общем случае круговая коническая поверхность включает в себя две совершенно одинаковые полости, которые имеют общую вершину. Образующие одной полости представляют собой продолжение образующих другой полости.
Бывают различные случаи сечения поверхности кругового конуса плоскостью.
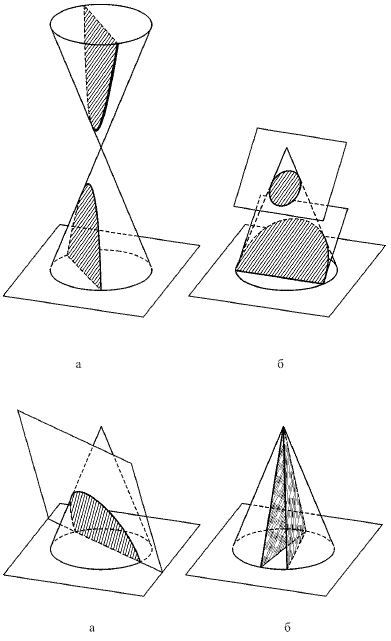
1. Эллипс, если секущая плоскость не параллельна ни одной образующей (рис. 107 б). Здесь секущая плоскость пересекает поверхность только одной полости конуса. Угол наклона секущей плоскости по отношению к основанию конуса меньше угла, который образующая конуса составляет с основанием конуса. Здесь угол является углом, который образующая составляет с основанием.
Рис. 107. Различные случаи сечения поверхности кругового конуса плоскостью: а – гипербола; б – эллипс; в – парабола; г – пара прямых
2. Парабола, если секущая плоскость параллельна только одной образующей (рис. 107 в).
3. Гипербола, если секущая плоскость параллельна двум образующим (рис. 107 а). При этом секущая плоскость пересекает обе полости конуса. Угол наклона секущей плоскости по отношению к основанию конуса больше угла.
4. Пара прямых, если секущая плоскость проходит через вершину конуса и угол ее наклона к основанию конуса больше угла. Этот случай иногда рассматривают как частный случай гиперболы.
Сечение шара
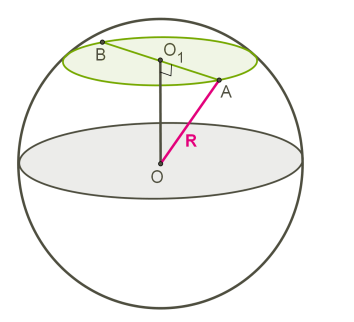
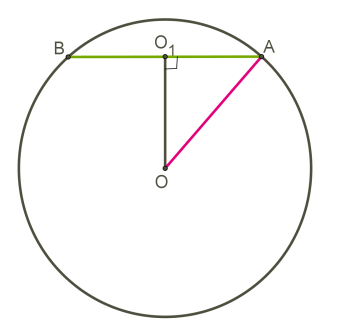
Всякое сечение шара плоскостью есть круг (или точка, если плоскость касается шара). Основание перпендикуляра, проведенного из центра шара к пересекаемой плоскости, есть центр круга, полученного в сечении.
При решении заданий удобнее вместо шара чертить один из больших кругов, а плоскость сечения заменить хордой этого круга.
Плоскость, проходящая через центр сферы (шара), называется диаметральной плоскостью.
Сечение сферы (шара) диаметральной плоскостью называется большой окружностью (большим кругом).













Warning: Use of undefined constant expert_review_likes - assumed 'expert_review_likes' (this will throw an Error in a future version of PHP) in /var/www/www-ars1963/data/www/ck62.ru/wp-content/themes/colormag/comments.php on line 93