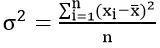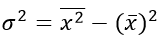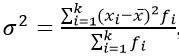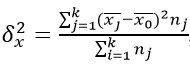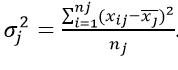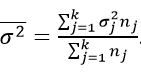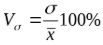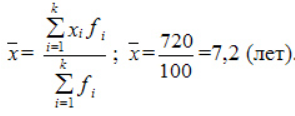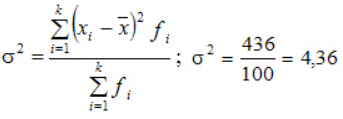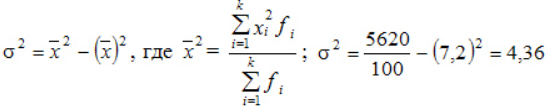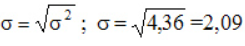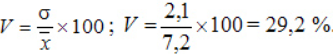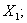какое свойство не всегда справедливо для дисперсии
Что такое дисперсия в статистике
Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.
Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.
Характеристики равномерного распределения представлены на картинке:
При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.
Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.
Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.
В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.
Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.
Виды дисперсии дискретной случайной величины
Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.
Общая дисперсия
Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.
Простая дисперсия, без разделения на группы:
Или в несколько преобразованном виде:
Взвешенная дисперсия, для вариационного ряда:
где xi – значение из ряда;
fi – частота, количество повторений;
n – число вариантов.
Черта сверху указывает на среднюю величину.
Межгрупповая дисперсия
Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».
Как найти данную дисперсию? По формуле:
где k – количество групп;
nj – элементов в группе с индексом j.
Внутригрупповая дисперсия
Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».
Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.
В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.
Если вычислить среднюю величину от всех групповых,
то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.
Взаимосвязь
В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.
Свойства дисперсии
Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.
Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ 2 можно по отклонениям от фиксированного числа.
Уменьшение всех цифр в k раз приведет к падению D[X] в k 2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.
Показатели вариаций
Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:
Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.
Пример расчета дисперсии
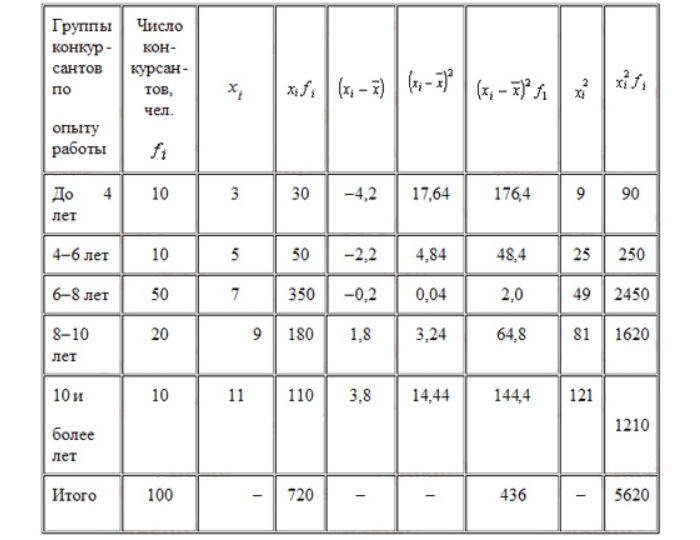
Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.
По альтернативной формуле:
Заключение
Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.
Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.
Математика — онлайн помощь
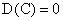
Данное свойство очевидно, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяния, конечно, не имеет.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:.
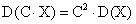
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:.
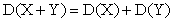
Данное свойство очевидно, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяния, конечно, не имеет.
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин..
Например, для трех слагаемых имеем:
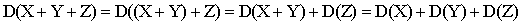
Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:.
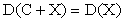
Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:.
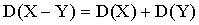
Рассмотрим следующую задачу. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна. Чему равна дисперсия числа появлений события в этих испытаниях? Ответ на этот вопрос дает следующая теорема.
ТЕОРЕМА 13.1.13. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:
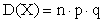
ПРИМЕР 13.1.38 Производятся 10 независимых испытаний, в каждом из которых вероятность появления события равна 0,6. Найти дисперсию случайной величины X — числа появлений события в этих испытаниях.
Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
1.17. Свойства дисперсии дискретной случайной величины
Для нахождения σ(Х) и V(X)% нужно предварительно найти D(Х) – дисперсию величины Х. При её нахождении полезно знать и использовать свойства дисперсии. Эти свойства таковы:
1. Дисперсия постоянной величины 

Доказательство. Согласно определения дисперсии (1.21) и свойства (1.5) при Х=С получаем:
Свойство (1.28) имеет очевидный смысл: константа разброса не имеет.
2. Постоянный множитель выносится из-под знака дисперсии в квадрате:

Доказательство. Согласно определения дисперсии (1.21) и свойства (1.6) математического ожидания получаем:
3. Дисперсия Суммы двух Независимых случайных величин равна сумме их дисперсий:

Доказательство. Используя упрощенную формулу (1.25) для дисперсии и доказанные выше свойства математического ожидания, получим:
4. Дисперсия разности двух Независимых случайных величин равна сумме их дисперсий:

Доказательство. Оно вытекает из уже доказанных свойств (1.29) и (1.30):
Дисперсия случайной величины, как мы знаем, характеризует степень разброса ее возможных значений вокруг ее среднего значения. Свойства 3 и 4, выражаемые равенствами (1.30) и (1.31), означают суммирование (увеличение) такого разброса как при сложении двух независимых случайных величин, так и при их вычитании, что вполне естественно.
Следствие 1 свойств 1– 4: Для любой дискретной случайной величины 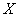

Доказательство. Так как 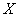

Следствие 2 свойств 1– 4: Если (

Это следствие докажите самостоятельно (за образец возьмите доказательство аналогичного равенства (1.13)).
1. К какому типу случайных величин (дискретным или непрерывным) принадлежат следующие величины:
А) Количество очков, выбиваемых стрелком при стрельбе по мишени в заданной серии выстрелов.
Б) Количество студентов студенческой группы, которые сдадут предстоящий экзамен.
В) Процент выполнения предприятием своего производственного задания.
Г) Количество осадков, которые выпадут ближайшим летом в данной местности.
Ответ: (а) и (б) – к дискретным, (в) и (г) – к непрерывным.
2. Станок-автомат производит в среднем 10% нестандартных деталей. Наудачу из его продукции отобраны три детали. Написать закон распределения дискретной случайной величины 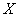




Дисперсия и ее свойства — справочник студента
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
Пример. Пусть случайные величины и имеют следующее законы распределения
Узнай стоимость своей работы
Найти математические ожидания и дисперсии этих случайных величин.
Решение. Воспользовавшись формулой для вычисления математических ожиданий, находим

С помощью формулы (2) вычислим дисперсии заданных случайных величин


Из полученных результатов делаем вывод: математические ожидания случайных величин и одинаковы, однако дисперсии различны. Дисперсия случайной величины мала и мы видим, что ее значение сконцентрированы около ее математического ожидания 

Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий
Узнай стоимость своей работы
Свойство 4. Дисперсия случайной величины равна математическому ожиданию
квадрата этой величины минус квадрат ее математического ожидания
Не нашли то, что искали? Воспользуйтесь поиском:
Дисперсия, виды и свойства дисперсии


Пример нахождения дисперсии
На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение
Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию


X min–минимальное значение группировочного признака;




Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.
Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок:
Подставляя в данную формулу дисперсии q =1- р, получаем:
Виды дисперсии
Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Внутригрупповая дисперсия характеризует случайную вариацию, т.е.
часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки.
Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.
Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:
где хi — групповая средняя;
ni — число единиц в группе.
Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:
Правило сложения дисперсии в статистике
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.
Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.
Свойства дисперсии
1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.
2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Дисперсия — свойства, виды и формулы

В различных научных дисциплинах словосочетание «дисперсия это» характеризует мало схожие понятия. С латыни «dispersio» переводится как «рассеяние».
В физике, например, означает связь фазовой скорости волны с частотой. В химии описывает несмешиваемые субстанции. В биологии – многообразие признаков популяции.
В данной статье речь пойдет о математической трактовке. Рассматривается как одно из свойств случайных величин.
Что такое дисперсия в статистике
Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.
Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.
Характеристики равномерного распределения представлены на картинке:
При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.
Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.
Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.
В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.
Кратко записывается D[X] в русскоязычных источниках и Var[X] (от «variance») в английских. В статистических выкладках используется σ2.
Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.
Виды дисперсии дискретной случайной величины
Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.
Общая дисперсия
Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.
Простая дисперсия, без разделения на группы:
Межгрупповая дисперсия
Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».
Как найти данную дисперсию? По формуле:
Внутригрупповая дисперсия
Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».
Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.
В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.
то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.
Взаимосвязь
В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.
Свойства дисперсии
Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.
Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ2 можно по отклонениям от фиксированного числа.
Уменьшение всех цифр в k раз приведет к падению D[X] в k2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.
Средний квадрат отклонений от постоянной величины X отличается в большую сторону от того же с использованием среднего значения. Разница составит (Xcр – X)2.
Показатели вариаций
Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:
Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.
Пример расчета дисперсии
Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.
Заключение
Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.
Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.
Дисперсия и ее оценка
Дисперсия – норма, отражающая, с точки зрения теории, ожидаемое отклонение случайной величины от ее математического ожидания.
В математической статистике она определяется в качестве центрального момента второго порядка. Приведем формулу дисперсии:
где М(х) – математическое ожидание, а D(х) – дисперсия.
На основе данной формулы можно вывести другую, которая дает оценку дисперсии:
где S2— оценка дисперсии, Xi— наблюдаемые значения, n – объем собранных эмпирических значений, X-— оценка математического ожидания.
В первой формуле оценка математического ожидания не смещена, но во второй формуле дисперсия является выборочной. Т.е. эта оценка дает характеристику величине дисперсии данной выборки, не для популяции данных. Обычно для эксперимента необходимо оценить популяционный характер математического ожидания и дисперсию.
Так как вторая формула предполагает сравнение эмпирических знаний не с истинной величиной, а с оценочной, то происходит смещение оценки дисперсии. Способами дифференциального исчисления определено: ожидаемая величина оценки дисперсии по второй формуле описывает соотношение:
Данная формула отражает выборочную дисперсию. Из нее следует, что при наличии 10 выборочных значений случайной величины идет занижение значения. Получается 9/10 дисперсий анализируемой величины для генеральной совокупности.
Если увеличить объем в десять раз, то уменьшиться величина смещения до одной сотой, и при этому полученный результат будет отличаться от ожидаемого значения.
При помощи третьей формулы можно рассчитать несмещенную оценку дисперсии:
Данная формула называется популяционной дисперсией, или дисперсией генеральной совокупности. Эту формулу используют для расчета генеральной совокупности, третью – для определения вариантов внутри выборки и выход за пределы имеющихся значений, который не предполагается теорией.
Характеристика оценивания стандартного отклонения
Иногда для оценивания важна не сама дисперсия, а оценка стандартного отклонения. Эти две величины связаны однозначным соотношением.
Оценивание стандартного отклонения также применяется для выборки и генеральной совокупности, как и дисперсия. Оценка данной величины является предпочтительной, так как она удобна для восприятия из-за своей размерности.
Помимо этого, эту величину используют для вычисления стандартной ошибки. Формула выглядит следующим образом:
где SE – стандартная ошибка.
Данная статистика необходима для интервальной оценки исследуемой случайной величины.
Характеристика оценки полумежквартильного интервала
Это еще один способ оценивания вариантов в распределении случайной величины. Ее обозначают Q. Она используется в качестве альтернативы стандартного отклонения, несмотря на то, что они связаны соотношением Q = 0,67σ.
Квартиль – это вариант названия квантиля распределения.
При соответствии медианы с половиной распределения, то квартиль равен четверти. Т.е. первая четверть – это первый квартиль, половина – второй квартиль, три четвертых – третий, общая сумма величины – четвертый квартиль. Формула межквартильного интервала выглядит следующим образом:
Данную оценку используют, например, в сенсорной психофизике при оценивании порога способом констант.
Характеристика ковариации
Иногда необходимо оценить не одну дисперсию, а две (х,у). Такая статистика называется ковариацией. Ее формула выглядит следующим образом:
Она определяет степень связи между двумя переменами. Отличительная особенность ковариации – это ее выражение и в положительных и в отрицательных числах.
Так как ковариация зависит от размерности, то оценить степень между переменными невозможно. Поэтому в качестве меры двух переменных используют термин «корреляция».
Ее величина может быть определена за счет деления ковариации на произведение стандартных отклонений двух случайных величин, между которыми вычисляют ковариацию.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Свойства дисперсии случайной величины
Дисперсией (рассеянием) дискретной случайной величиныD(X) называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
1 свойство. Дисперсия постоянной величины C равна нулю; D(C) = 0.
Доказательство. По определению дисперсии, D(C) = M<[C – M(C)]2>.
Доказательство. В силу третьего свойства D(X − Y) = D(X) + D(–Y). По второму свойству
D(X − Y) = D(X) + (–1)2 D(Y) или D(X − Y) = D(X) + D(Y)
Числовые характеристики систем случайных величин. Коэффициент корреляции, свойства коэффициента корреляции.
Корреляционный момент.Характеристикой зависимости между случайными величинами и служит математическое ожидание произведения отклонений и от их центров распределений (так иногда называют математическое ожидание случайной величины), которое называется корреляционным моментом или ковариацией:
Для вычисления корреляционного момента дискретных величин используют формулу:
а для непрерывных величин – формулу:
Коэффициентом корреляции rxy случайных величин X и Y называют отношение корреляционного момента к произведению среднеквадратичных отклонений величин: — коэффициент корреляции;
Свойства коэффициента корреляции:
1. Если Х и У независимые случайные величины, то r =0;
3. r характеризует относительную величину отклонения М(ХУ) от М(Х)М(У), и т.к. отклонение имеет место только для зависимых величин, то rхарактеризует тесноту зависимости.
Линейная функция регрессии.
Рассмотрим двумерную случайную величину (X, Y), где X и У — зависимые случайные величины. Представим одну из величин как функцию другой. Ограничимся приближенным представлением (точное приближение, вообще говоря, невозможно) величины Y в виде линейной функции величины X:
Все слагаемые этой суммы неотрицательны. Отбросим те слагаемые, у которых |xi – M(X)| https://infopedia.su/1x7d0.html
Дисперсия и стандартное отклонение в EXCEL
Вычислим в MS EXCEL дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Дисперсия выборки
Дисперсия случайной величины
где x i – значение, которое может принимать случайная величина, а μ – среднее значение ( математическое ожидание случайной величины ), р(x) – вероятность, что случайная величина примет значение х.
Стандартное отклонение выборки
По определению, стандартное отклонение равно квадратному корню из дисперсии :
Стандартное отклонение можно также вычислить непосредственно по нижеуказанным формулам (см. файл примера ) =КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Вычисления в функции СРОТКЛ () производятся по формуле:
Дисперсия и ее свойства
Дисперсия определяется по формулам
Она обладает рядом свойств:
3. Если уменьшить или увеличить все значения признака в постоянное число С, то дисперсия уменьшится или увеличится в квадрат этого числа раз, т.е.
Среднее квадратическое отклонение — это корень квадратный из дисперсии:
На практике обычно отклонения нс превышают За. Это положение называют правилом трех сигм.
Определить дисперсию, используя ее свойства.
| Выпуск продукции, млн руб. | Число предприятий / | х, | х’ | x’f | |
| 1-3 | 3 | 2 | -2 | -6 | 12 |
| 3-5 | 8 | 4 | -1 | -8 | 8 |
| 5-7 | 12 | 6 | 0 | 0 | 0 |
| 7-9 | 7 | 8 | +1 | +7 | 7 |
| I | 30 | — | — | -7 | 27 |
Определяем условное значение дисперсии:
Если необходимо определить дисперсию для нескольких рядов, то можно воспользоваться формулой сложения дисперсий:
где ст^, г — межгрупповая дисперсия, определяемая по формуле
где х< — средняя арифметическая в каждой i-й группе; щ —количество признаков в группе; лг0 — общая средняя, определяемая по формуле
ст в.г — средняя из внутригрупповых дисперсий, определяемая по формуле
где — внутригрупповая дисперсия, определяемая по формуле
Определить внутригрупповую, межгрупповую и общую дисперсии.
| Группа | Разряд рабочих в бригадах | X | |||||
| Х | 2 | 5 | 6 | 3 | 2 | 3 | 21 |
| (*i-*)2 | 2,25 | 2,25 | 6,25 | 0,25 | 2,25 | 0,25 | 13,5 |
| *2 | 3 | 4 | 4 | 5 | 3 | 4 | 23 |
| (х2 — х)2 | 0,64 | 0,04 | 0,04 | 1,44 | 0,64 | 0,04 | 2,84 |
| Группа | Разряд рабочих в бригадах | Е | |||||
| *3 | 5 | 6 | 6 | 2 | 2 | 3 | 24 |
| (*з — *)2 | 1 | 4 | 4 | 4 | 4 | 1 | 18 |
Определяем средние арифметические величины для каждой группы:
Средняя из внутригрупповых дисперсий Межгрупповая дисперсия Общая дисперсия