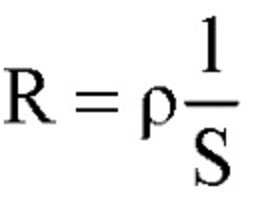какое сопротивление больше 2ом или 4 ом
Основы автоэлектрики. Часть2. Резисторы. Провода. Подробнее о сопротивлении
Ранее мы изучили самые базовые основы электротехники:
Основы автоэлектрики. Часть1. Основные законы
Сегодня мы поговорим о таком простом и популярном электронном компоненте как резистор, немного о проводах и о законах сопротивления.
Оглавление сегодняшнего материала:
1. Резистор постоянный.
2. Провод как резистор.
3. Последовательное включение резисторов.
4. Параллельное включение резисторов.
5. Смешанное (последовательно-параллельное) включение резисторов.
6. Преобразование «звезда-треугольник».
7. Маркировка резисторов.
Данный материал служит продолжением описания некоторой фундаментальной базы знаний по автоэлектрике. Не обязательно приведённые формулы и правила маркировки элементов автоэлектрик должен знать наизусть. Но иметь представление об этом материале, знать, где искать эту информацию и как ей правильно пользоваться, должен каждый электрик или электронщик.
1. Резистор постоянный.
Резистор постоянный — это электронный компонент с постоянным сопротивлением.
Его основными характеристиками являются:
— Номинальное значение сопротивление, Ом
— Допускаемое производителем отклонение от номинального значения, %
— Максимально допустимая мощность рассеяния (о мощности мы погорим позже), Вт
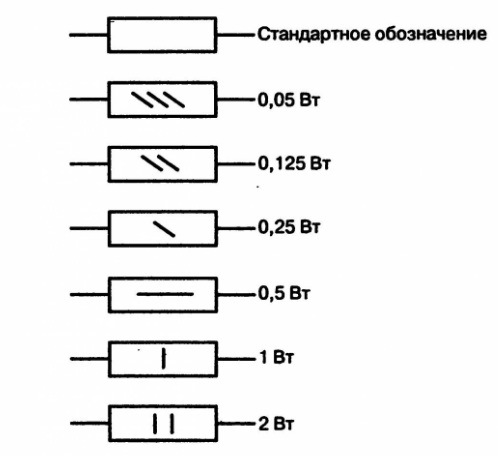
Его обозначение на схемах (условное графическое обозначение) выглядит следующим образом:
Резисторы могут иметь несколько видов корпусов:
2. Провод как резистор
Во многих идеализированных схемах провод имеет сопротивление, равное 0 Ом. На практике же это не совсем так (или даже: сосем нетак). Если постоянно принимать значение провода, равным нулю, можно попасть в очень неприятные ситуации, особенно, когда речь идёт об автоэлектрике. Дело в том, что проводник обычно подбирают таким, чтобы его значение было значительно ниже сопротивление цепи, тогда можно будет принимать значение его сопротивления, равным нулю.
Сопротивление проводника считается по формуле, которую мы изучили в прошлый раз:
, где l — длины проводника, S — площадь поперечного сечения проводника, р — удельное сопротивление.
Основные выводы из данной формулы:
— чем длиннее провод, тем выше его сопротивление.
— чем больше сечение (толще провод), тем ниже сопротивление.
Когда проводник выполняет функцию провода (кабеля, шнура), то с точки зрения электротехники работает правило «Чем меньше сопротивление, тем лучше». И идеальный провод — это проводник с сопротивлением 0 Ом. Но мы живём в реальном мире, в котором такого проводника не существует.
По этой причине провод следует рассматривать как резистор с неким сопротивлением.
О том, почему горят провода, как правильно подбирать провод и почему помогает в некоторых вопросах элементарная замена, казалось бы, целого провода или переобжимка его клемм, мы поговорим более детально дальше, когда будем касаться вопроса мощности. Но сразу скажу, что связь с сопротивлением провода тут прямая.
3. Последовательное включение резисторов
Первый из законов сопротивлений, который мы сегодня рассмотрим, связан с последовательным включением резисторов и проводов.
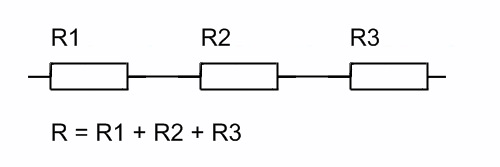
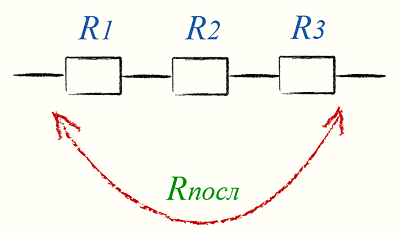
Последовательное включение резисторов приводит к суммированию сопротивлений.
На схеме это может выглядеть так:
Если, к примеру, мы имеем три резистора сопротивлением 10 кОм, то суммарное сопротивление всей цепи от начала до конца будет равно 30 кОм.
4. Параллельное включение резисторов
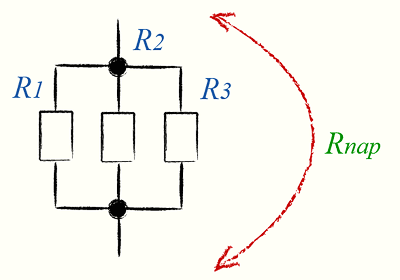
Второй закон сопротивлений связан с параллельным включением резисторов и проводов:
Общее сопротивление цепи, состоящей из параллельных резисторов, считается по формуле:
1/R = 1/R1 + 1/R2 + … + 1/RN.
Пусть мы имеем три резистора сопротивлением 3 кОм, включенных параллельно. Тогда общее сопротивление полученной цепи вычисляется по следующей формуле:
1/R = 1/R1 + 1/R2 + 1/R3
1/R = 1/3000 + 1/3000 + 1/3000 = 3/3000 = 1/1000
Откуда:
R = 1000 Ом, или же R = 1кОм.
Когда все резисторы в параллельной цепи имеют одинаковое сопротивление (т.е. R1=R2=…=RN), суммарное сопротивление высчитывается легко:
R = R1/N, где N — количество резисторов.
При параллельном включении ВСЕГДА суммарное сопротивление всей цепи ниже, чем сопротивление любого из включенного в цепь резистора. Отсюда следует вывод, что параллельное включение — это один из способов снижения суммарного сопротивления цепи. Данное применение можно увидеть в многожильном кабеле:
Следует отметить, что обламывание отдельных жил в таком кабеле приводит к увеличению сопротивления провода.
5. Смешанное (последовательно-параллельное) включение резисторов.
Если существует два изученных типа включений, то возникает вопрос, почему не может существовать смешанное включение? Ответ на вопрос очевиден: может и, более того, существует.
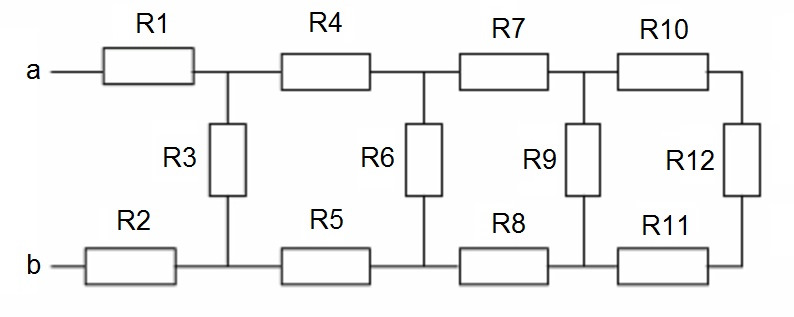
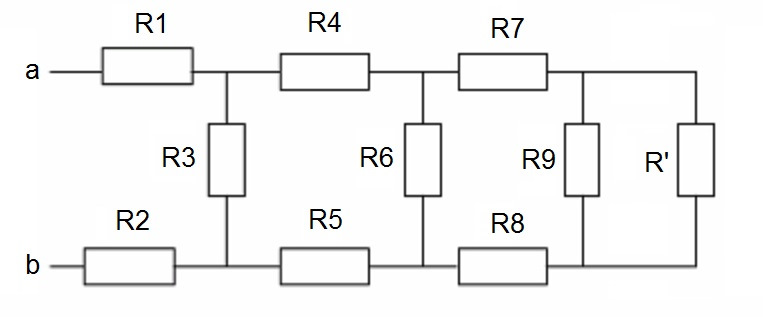
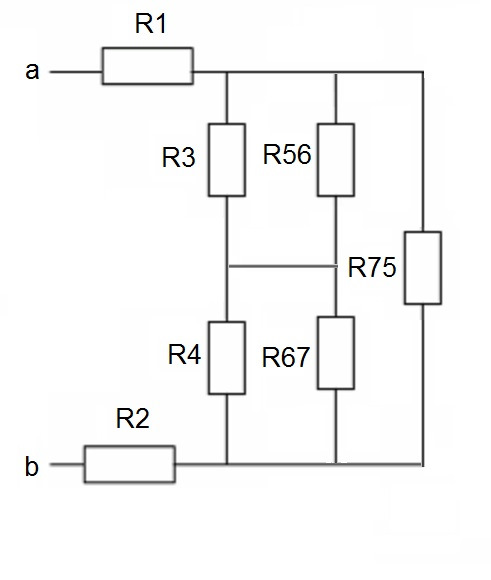
Представим себе одну из таких цепей, состоящей из двенадцати резисторов:
И нам необходимо понять, какое сопротивление всей цепи, если подключимся Омметром к точкам «a» и «b».
Неподготовленному зрителю картинка может показаться ужасающей. Но не всё так сложно, когда мы знаем правила параллельных и последовательных включений.
Смотрим на схему:
Первое, что следует отметить — это последовательное включение трёх резисторов: R10, R11 и R12.
Значит их суммарное сопротивление будет равно:
R’ = R10 + R11 + R13.
Эквивалентно на схеме эти три резистора можно заменить на одно с сопротивлением R’:
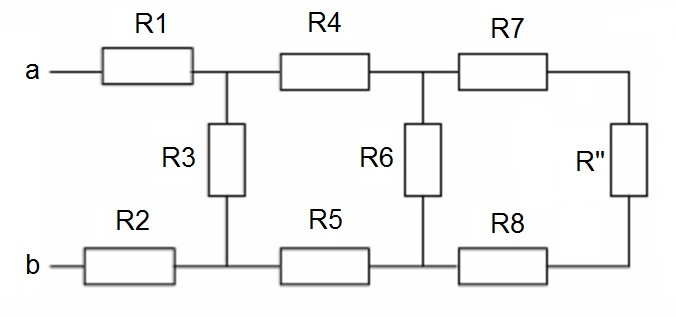
Далее мы видим, что R9 и R’ включены параллельно. Т.е. их суммарное сопротивление будет равно:
Далее опять можно заменить резисторы R9 и R’ на одно эквивалентное сопротивление R»:
Ну, а дальше все аналогичным образом:
Ну, и в конечном счете:
Как видно, ничего сложного в задачах подобного рода нет. Кроме того, на втором курсе университета с упоением считал настолько сложные конфигурации из решебника, даже те, что не задавались на дом=)
Это напоминает своего рода игру — лабиринт или судоку=)
6. Преобразование звезда-треугольник.
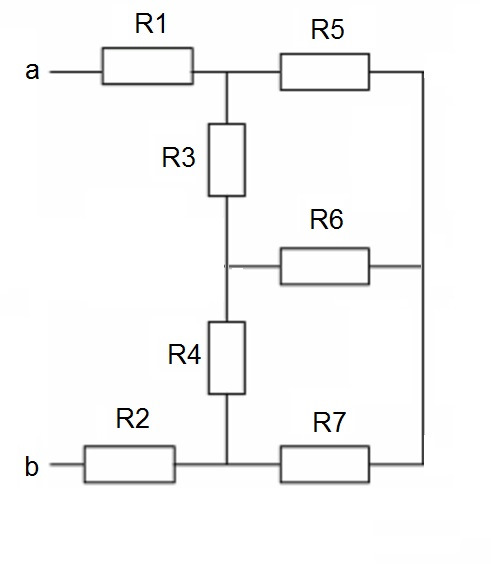
Представьте ситуацию: вы смотрите на смешанное включение резисторов, но понять как вести расчет, используя правила для последовательного и параллельного включения, вы не можете:
Тут не видно явных параллельных и последовательных включений.
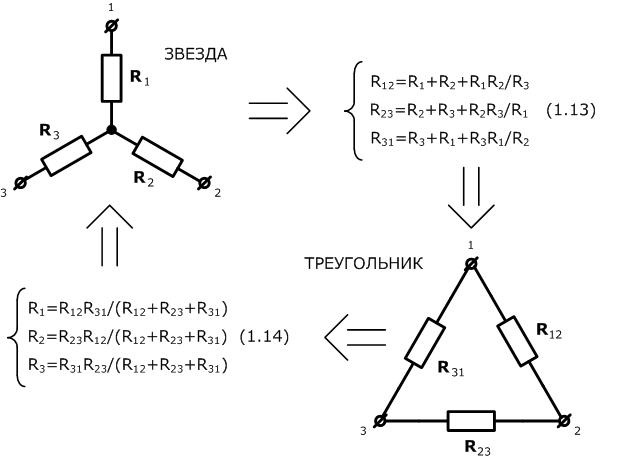
В таких случаях на помощь приходит замечательный механизм преобразований «звезда-треугольник»:
Возвращаемся к нашему рисунку и мы видим, что R5, R6 и R7 образуют звезду.
Преобразовав в треугольник, мы получим следующее:
R56 = R5 + R6 + R5*R6/R7
R67 = R6 + R7 + R6*R7/R5
R75 = R7 + R5 + R7*R5/R6
Ну, а дальше схема приобретает вид, который спокойно решается правилами последовательного и параллельного включения:
R’ = 1/(1/R3 + 1/R56)
R» = 1/(1/R4 + 1/R67)
R»’ = R’ + R»
R»» = 1/(1/R75 + 1/R»’)
7. Маркировка резисторов
Решать задачи, конечно, хорошо. Кому очень хочется порешать задачи такого рода, может обратиться в любой книжный магазин и приобрести задачник по электротехнике или скачать таковой с просторов сети.
Но мы опять же с Вами возвращаемся в реальность — в наши квартиры, офисы, гаражи, где перед нами появилось устройство с резисторами. Как же определить номинал? Напомню (об этом упоминалось в прошлой части курса), что для проверки сопротивления Омметром необходимо не только обесточить цепь, но и извлечь и цепи резистор (хотя бы отпаять одну ножку). Почему необходимо извлекать резистор (лампочка накала, кстати, тоже отчасти резистор), ясно из проведённых схемных преобразований. Попытка проверить Омметром приведет к значению на неких двух точках А и В, которое нужно высчитать, зная значения всех сопротивлений цепи.
Если на выводном (т.е. с ножками) резисторе имеются буквы, то гадать долго не придётся:
12Ω, 12J, 12 — означают 12 Ом
12kΩ, 12k — означают 12 кОм
1k2Ω, 1k2 — означают 1,2 кОм
R12 — означает 0,12 Ом
И так далее.
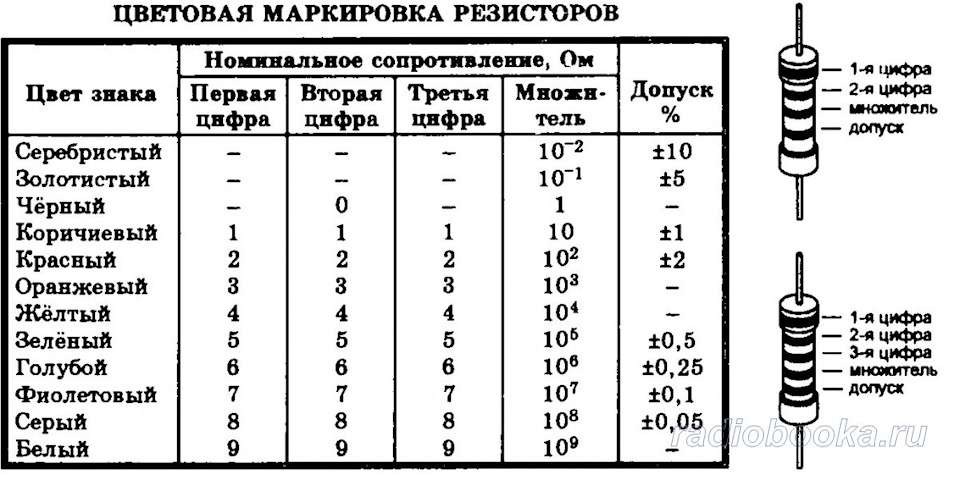
Также для выводных резисторов характерно обозначение цветами:
Тогда читать их нужно так:
Для чип-резисторов характерно трехзначное цифровое обозначение, типа 123, 560 и так далее:
123 — это 12*10^3 Ом, т.е. 12 кОм.
560 — это 56*10^0 Ом, т.е. 56 Ом
Если на чип-резисторе 4 цифры, типа 7122, то считается это так:
7122 = 712*10^2 = 71,2 кОм
Если же маркировка на чипе буквено-цифровая (две цифры и буква или буква и две цифры), то тут всё гораздо сложнее и для получения значения потребуется воспользоваться специальными таблицами типа EIA-96).
Логике особой сходу значения не поддаются, поэтому гадать даже не пытайтесь.
К примеру,
D12 — это 300 кОм,
12D — это 130 кОм
B51 — это 1,5 кОм
51B — это 3320 Ом
Что такое импеданс колонок и как подобрать усилитель по этому параметру
Содержание
Содержание
Про импеданс обычно узнают при выборе усилителя для набора комнатной акустики или автомобильных колонок. Чем важен этот параметр, что от него зависит? Что лучше — высокий или низкий импеданс, отражается ли это на звуке, и что произойдет, если колонки с низким импедансом подключить к усилителю, рассчитанному на высокий? Обо всем этом ниже.
Что такое импеданс
Строго говоря, импеданс представляет собой полное электрическое сопротивление акустической системы. Она обычно состоит из динамиков и кроссоверов, у которых за счет электромагнитной катушки и небольшого набора радиодеталей есть определенное сопротивление постоянному току. Однако звук в проводах представляет собой ток переменный, соответственно, при разной частоте сигнала сопротивление будет разным. Чтобы избежать путаницы, импеданс акустики обычно измеряется на частоте 1000 Гц. Таким образом, термины «сопротивление» и «импеданс» тождественны.
В общем и целом, импеданс говорит о том, насколько сложно будет усилителю нагрузить динамик и какую нагрузку он предоставляет усилителю. При этом действует правило:
Чем меньше импеданс динамика/колонки, тем сложнее усилителю будет ее нагрузить.
То есть, динамик с сопротивлением 4 Ом усилителю будет сложнее раскачать, чем динамик с импедансом 8 Ом. Это следует из закона Ома: напряжение, деленное на сопротивление, дает силу тока. Т. е. сила тока обратно пропорциональна сопротивлению в цепи. Если последнее снижается, то либо току, либо напряжению нужно увеличиваться, чтобы сохранить тот же уровень громкости.
Импеданс можно измерить и в домашних условиях: понадобится аудиокарта, усилитель, динамик и соответствующий софт. В результате получится график, который, к удивлению экспериментатора, может быть далек от паспортных данных.
Обычно импеданс имеет большой горб в области баса из-за резонансов и плавно растет на высоких — из-за реактивного сопротивления магнитной катушки динамика. На пиках сопротивление может подскакивать намного выше заявленных характеристик, что нужно учитывать при конструировании концертных залов и студий. Однако это не является большой проблемой для домашней акустики, если не эксплуатировать ее на пределе возможностей.
Почему импеданс важен?
Согласованность усилителя и колонок по импедансу обеспечит безопасную и долговечную работу обоих приборов, избавит от проблем и искажений звука. В свою очередь, если подключить колонки с импедансом в пару Ом к усилителю, рассчитанному минимум на 8 Ом, и включить громкую музыку, тогда динамикам можно сказать до свидания.
Помимо этого, мощность усилителя на выходе напрямую зависит от импеданса акустики: чем выше импеданс, тем меньше мощность. Например, усилитель, выдающий по 50 Вт на канал с колонками на 4 Ом, обеспечит лишь по 25 Вт на колонку с импедансом 8 Ом. Грубо говоря, в первом случае будет громче. Часто в спецификациях усилителя указывается, какова будет его мощность в сочетании с акустикой, исходя из базовых значений импеданса.
Что лучше — высокий или низкий импеданс?
Ценители качественного звука обычно предпочитают колонки с более высоким импедансом. Эта традиция отчасти идет от наушников: там студийные и аудиофильские модели имеют импеданс в 300 и более Ом. Считается, что высокоомная нагрузка более благоприятна для усилителя, так он выдает меньше искажений.
В автозвуке и бытовой акустике, где мощность важнее нюансов звучания, чаще выбирают акустику с более низким импедансом. Но здесь стоит помнить, что чем ниже импеданс, тем большую роль в общем сопротивлении играют провода. Отчасти поэтому аудиофилы уделяют им так много внимания и предпочитают высокое сопротивление динамиков.
Тем не менее, в конечном счете, куда важнее оказывается качество изготовления прибора, а не его импеданс, а также правильное согласование усилителя и громкоговорителей.
Как подобрать усилитель по импедансу?
На самом деле с импедансом все просто. В большинстве случаев сопротивление и колонок, и усилителей находится в диапазоне 4-8 Ом, так что долго ломать голову с выбором не придется. Стандарты динамиков для автозвука — 2, 3 и 4 Ом. При выборе усилителя нужно, чтобы колонки подпадали под этот диапазон. При этом:
Нестандартные значения импеданса бывают, в основном, в экзотических аудиофильских системах. Бывают и многоканальные усилители, в которых сопротивление на канал можно переключать самостоятельно в определенном диапазоне. Яркий пример — гитарные усилители, которые имеют отдельные выходы для динамиков с разным сопротивлением.
Как подогнать импеданс под усилитель?
Есть простой хинт, позволяющий точно согласовать почти любые колонки с любым усилителем. Если импеданс колонок слишком высок, нужно подключить их к усилку параллельно, а если слишком низкий — последовательно:
Также можно использовать комбинации последовательного и параллельного подключения, если динамиков много. Есть и специальные приборы, которые упрощают коммутацию и предлагают гибкость в выборе нужного импеданса.
Некоторые также используют обычный резистор, чтобы подогнать импеданс под нужное значение. К примеру, если импеданс колонок всего 2 Ом, а усилитель рассчитан на 4-16 Ом, тогда резистор на пару Ом может решить дело для тех, кто знаком с радиотехникой и понимает, какой провод куда идет. В фирменных приборах с выбором импеданса внутри находится как раз пара резисторов, прикрепленных к радиаторам, чтобы не перегревались при нагрузке.
Мостовое подключение
Мост позволяет подключить мощные колонки или, чаще всего, сабвуфер к усилителю, поддерживающему соответствующую функцию (об этом должно быть написано в мануале). Суть его очень проста: к динамику подключается плюс от одного канала и минус от другого канала усилителя. Таким образом левый и правый каналы объединяются в один моноканал, мощность которого в 4 раза выше каждого по отдельности.
На что еще смотреть при выборе усилителя?
Помимо импеданса, нужно учесть мощность и чувствительность.
Мощность — это квадрат напряжения, поделенный на сопротивление, измеряется в ваттах. Обычно в спецификациях указывают номинальную и пиковую мощность, в этом случае нужно смотреть на номинальную: она показывает, грубо говоря, насколько громким будет усилитель при обычном режиме работы. К примеру, 200 Вт при 4 Ом. При согласовании мощности нужно быть внимательным:
Грубо говоря, если акустика имеет номинальную мощность 50 Вт, то номинальная мощность усилителя должна примерно ей соответствовать. Некий разброс при этом допустим и не критичен, если нет задачи слушать музыку подолгу на максимальной громкости.
Параметр чувствительности относится только к колонкам и определяет, как громко будет звучать колонка на расстоянии в 1 м, если подать на нее 1 Вт. Чувствительность измеряется в децибелах. Чем ниже чувствительность колонок/динамиков, тем тише они звучат, тем более мощный усилитель им нужен. Высокая чувствительность снижает требования к усилителю.
Заключение
Активная акустика со встроенным усилителем лидирует в сегменте бытовых колонок. Она избавляет от необходимости подбирать одно к другому и полностью исключает риск роковой ошибки. Поэтому об импедансе чаще всего задумываются любители автозвука, которым приходится выбирать динамики и усилитель по отдельности, либо аудиофилы, которые строят свою кастомную систему. В обоих случаях достаточно посмотреть, сколько мощности выдаст усилитель на импедансе выбранных колонок, и проверить по их номинальной мощности, не надорвутся ли динамики от такой нагрузки.
Резистор и сопротивление
Каталог
Показать каталог
Резистор и сопротивление
Теория
КОМПОНЕНТЫ
ARDUINO
RASPBERRY
ИНТЕРФЕЙСЫ ПЕРЕДАЧИ ДАННЫХ
1 кОм = 1000 Ом,
1 МОм = 1000 кОм,
1 ГОм = 1000 МОм
Последовательное соединение резисторов
Это справедливо и для большего количества соединённых последовательно резисторов:
Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.
При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.
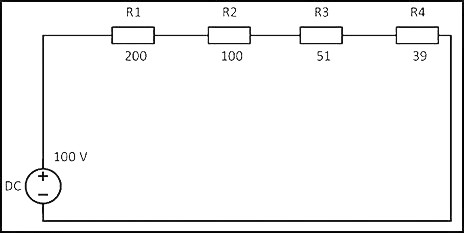
Мощность при последовательном соединении
R = 200 + 100 + 51 + 39 = 390 Ом
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять
I = U/R = 100 В/390 Ом = 0,256 A
На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле:
P = I 2 x R = 0,256 2 x 390 = 25,55 Вт
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощности, то общая Р составит:
Робщ = 13,11 + 6,55 + 3,34 + 2,55 = 25,55 Вт
Параллельное соединение резисторов
Расчет параллельного сопротивления двух параллельно соединённых резисторов R1 и R2 производится по следующей формуле:
Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:
Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.
Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.
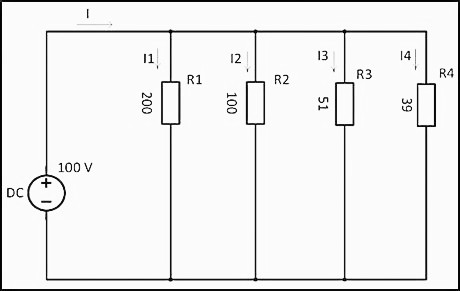
Мощность при параллельном соединении
1/R = 1/200 + 1/100 + 1/51 + 1/39 ≈ 0,06024 Ом
R = 1 / 0,06024 ≈ 16,6 Ом
Используя значение напряжения 100 В, по закону Ома рассчитывается сила тока
I = U/R = 100 В x 0,06024 Ом = 6,024 A
Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом
P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт
Расчет силы тока для каждого резистора выполняется по формулам:
На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов:
P1 = U 2 /R1 = 100 2 /200 = 50 Вт;
P2 = U 2 /R2 = 100 2 /100 = 100 Вт;
P3 = U 2 2/R3 = 100 2 /51 = 195,9 Вт;
P4 = U 2 2/R4 = 100 2 /39 = 256,4 Вт
Если сложить полученные мощности, то общая Р составит:
Робщ = 50 + 100 + 195,9 + 256,4 = 602,3 Вт
Резистор. Резисторы постоянного сопротивления
Здравствуйте, уважаемые читатели сайта sesaga.ru. В предыдущей статье мы разобрались, какие бывают соединительные провода и линии электрической связи и как они обозначаются на электрических схемах. В этой статье речь пойдет о резисторе или как по старинке его еще называют сопротивление.
Резисторы являются наиболее распространенными элементами радиоэлектронной аппаратуры и используются практически в каждом электронном устройстве. Резисторы обладают электрическим сопротивлением и служат для ограничения прохождения тока в электрической цепи. Их применяют в схемах делителей напряжения, в качестве добавочных сопротивлений и шунтов в измерительных приборах, в качестве регуляторов напряжения и тока, регуляторов громкости, тембра звука и т.д. В сложных приборах количество резисторов может достигать до нескольких тысяч штук.
1. Основные параметры резисторов.
Основными параметрами резистора являются: номинальное сопротивление, допускаемое отклонение фактической величины сопротивления от номинального (допуск), номинальная мощность рассеивания, электрическая прочность, зависимость сопротивления: от частоты, нагрузки, температуры, влажности; уровня создаваемых шумов, размерами, массой и стоимостью. Однако на практике резисторы выбирают по сопротивлению, номинальной мощности и допуску. Рассмотрим эти три основных параметра более подробно.
1.1. Сопротивление.
Сопротивление — это величина, которая определяет способность резистора препятствовать протеканию тока в электрической цепи: чем больше сопротивление резистора, тем большее сопротивление он оказывает току, и наоборот, чем меньше сопротивление резистора, тем меньшее сопротивление он оказывает току. Используя эти качества резисторов их применяют для регулирования тока на определенном участке электрической цепи.
Сопротивление измеряется в омах (Ом), килоомах (кОм) и мегаомах (МОм):
1кОм = 1000 Ом;
1МОм = 1000 кОм = 1000000 Ом.
Промышленностью выпускаются резисторы различных номиналов в диапазоне сопротивлений от 0,01 Ом до 1ГОм. Числовые значения сопротивлений установлены стандартом, поэтому при изготовлении резисторов величину сопротивления выбирают из специальной таблицы предпочтительных чисел:
Нужное числовое значение сопротивления получают путем деления или умножения этих чисел на 10.
Номинальное значение сопротивления указывается на корпусе резистора в виде кода с использованием буквенно-цифровой, цифровой или цветовой маркировки.
При использовании буквенно-цифровой маркировки единицу измерения Ом обозначают буквами «Е» и «R», единицу килоом буквой «К», а единицу мегаом буквой «М».
а) Резисторы с сопротивлениями от 1 до 99 Ом маркируют буквами «Е» и «R». В отдельных случаях на корпусе может указываться только полная величина сопротивления без буквы. На зарубежных резисторах после числового значения ставят значок ома «Ω»:
б) Резисторы с сопротивлениями от 100 до 999 Ом выражают в долях килоома и обозначают буквой «К». Причем букву, обозначающую единицу измерения, ставят на месте нуля или запятой. В некоторых случаях может указываться полная величина сопротивления с буквой «R» на конце, или только одно числовое значение величины без буквы:
К12 = 0,12 кОм = 120 Ом
К33 = 0,33 кОм = 330 Ом
К68 = 0,68 кОм = 680 Ом
360R — 360 Ом
в) Сопротивления от 1 до 99 кОм выражают в килоомах и обозначают буквой «К»:
г) Сопротивления от 100 до 999 кОм выражают в долях мегаома и обозначают буквой «М». Букву ставят на месте нуля или запятой:
М18 = 0,18 МОм = 180 кОм
М47 = 0,47 МОм = 470 кОм
М91 = 0,91 МОм = 910 кОм
д) Сопротивления от 1 до 99 МОм выражают в мегаомах и обозначают буквой «М»:
е) Если номинальное сопротивление выражено целым числом с дробью, то буквы Е, R, К и М, обозначающие единицу измерения, ставят на месте запятой, разделяя целую и дробную части:
Цветовая маркировка обозначается четырьмя или пятью цветными кольцами и начинается слева направо. Каждому цвету соответствует свое числовое значение. Кольца сдвинуты к одному из выводов резистора и первым считается кольцо, расположенное у самого края. Если размеры резистора не позволяют разместить маркировку ближе к одному из выводов, то ширина первого кольца делается примерно в два раза больше других.
Отчет сопротивления резистора ведут слева направо. Резисторы с величиной допуска ±20% (о допуске будет сказано ниже) маркируются четырьмя кольцами: первые два обозначают численную величину сопротивления в Омах, третье кольцо является множителем, а четвертое — обозначает допуск или класс точности резистора. Четвертое кольцо наносится с видимым разрывом от остальных и располагается у противоположного вывода резистора.
Резисторы с величиной допуска 0,1…10% маркируются пятью цветовыми кольцами: первые три – численная величина сопротивления в Омах, четвертое – множитель, и пятое кольцо – допуск. Для определения величины сопротивления пользуются специальной таблицей.
Например. Резистор маркирован четырьмя кольцами:
красное — (2)
фиолетовое — (7)
красное — (100)
серебристое — (10%)
Значит: 27 Ом х 100 = 2700 Ом = 2,7 кОм с допуском ±10%.
Резистор маркирован пятью кольцами:
красное — (2)
фиолетовое (7)
красное (2)
красное (100)
золотистое (5%)
Значит: 272 Ома х 100 = 27200 Ом = 27,2 кОм с допуском ±5%
Иногда возникает трудность с определением первого кольца. Здесь надо запомнить одно правило: начало маркировки не будет начинаться с черного, золотистого и серебристого цвета.
И еще момент. Если нет желания возиться с таблицей, то в интернете есть программы онлайн калькуляторы, предназначенные для подсчета сопротивления по цветным кольцам. Программы можно скачать и установить на компьютер или смартфон. Также о цветовой и буквенно-цифровой маркировке можно почитать в этой статье.
Цифровая маркировка наносится на корпуса SMD компонентов и маркируется тремя или четырьмя цифрами.
При трехзначной маркировке первые две цифры обозначают численную величину сопротивления в Омах, третья цифра обозначает множитель. Множителем является число 10 возведенное в степень третьей цифры:
221 – 22 х 10 в степени 1 = 22 Ом х 10 = 220 Ом;
472 – 47 х 10 в степени 2 = 47 Ом х 100 = 4700 Ом = 4,7 кОм;
564 – 56 х 10 в степени 4 = 56 Ом х 10000 = 560000 Ом = 560 кОм;
125 – 12 х 10 в степени 5 = 12 Ом х 100000 = 12000000 Ом = 12 МОм.
Если последняя цифра ноль, то множитель будет равен единице, так как десять в нулевой степени равно единице:
100 – 10 х 10 в степени 0 = 10 Ом х 1 = 10 Ом;
150 – 15 х 10 в степени 0 = 15 Ом х 1 = 15 Ом;
330 – 33 х 10 в степени 0 = 33 Ом х 1 = 33 Ом.
При четырехзначной маркировке первые три цифры также обозначают численную величину сопротивления в Омах, а четвертая цифра обозначает множитель. Множителем является число 10 возведенное в степень четвертой цифры:
1501 – 150 х 10 в степени 1 = 150 Ом х 10 = 1500 Ом = 1,5 кОм;
1602 – 160 х 10 в степени 2 = 160 Ом х 100 = 16000 Ом = 16 кОм;
3243 – 324 х 10 в степени 3 = 324 Ом х 1000 = 324000 Ом = 324 кОм.
1.2. Допуск (класс точности) резистора.
Вторым важным параметром резистора является допускаемое отклонение фактического сопротивления от номинального значения и определяется допуском (классом точности).
Допускаемое отклонение выражается в процентах и указывается на корпусе резистора в виде буквенного кода, состоящего из одной буквы. Каждой букве присвоено определенное числовое значение допуска, пределы которого определены ГОСТ 9964-71 и приведены в таблице ниже:
Наиболее распространенные резисторы выпускаются с допуском 5%, 10% и 20%. Прецизионные резисторы, применяемые в измерительной аппаратуре, имеют допуски 0,1%, 0,2%, 0,5%, 1%, 2%. Например, у резистора с номинальным сопротивлением 10 кОм и допуском 10% фактическое сопротивление может быть в пределах от 9 до 11 кОм ±10%.
На корпусе резистора допуск указывается после номинального сопротивления и может состоять из буквенного кода или цифрового значения в процентах.
У резисторов с цветовой маркировкой допуск указывается последним цветным кольцом: серебристый цвет – 10%, золотистый – 5%, красный – 2%, коричневый – 1%, зеленый – 0,5%, голубой – 0,25%, фиолетовый – 0,1%. При отсутствии кольца допуска резистор имеет допуск 20%.
1.3. Номинальная мощность рассеивания.
Третьим важным параметром резистора является его мощность рассеивания
При прохождении тока через резистор на нем выделяется электрическая энергия (мощность) в виде тепла, которое сначала повышает температуру тела резистора, а затем за счет теплопередачи переходит в воздух. Поэтому мощностью рассеивания называют ту наибольшую мощность тока, которую резистор способен длительное время выдерживать и рассеивать в виде тепла без ущерба потери своих номинальных параметров.
Поскольку слишком высокая температура тела резистора может привести его к выходу из строя, то при составлении схем задается величина, которая указывает на способность резистора рассеивать ту или иную мощность без перегрева.
За единицу измерения мощности принят ватт (Вт).
Например. Допустим, что через резистор сопротивлением 100 Ом течет ток 0,1 А, значит, резистор рассеивает мощность в 1 Вт. Если же резистор будет меньшей мощности, то он быстро перегреется и выйдет из строя.
В зависимости от геометрических размеров резисторы могут рассеивать определенную мощность, поэтому резисторы разной мощности отличаются размерами: чем больше размер резистора, тем больше его номинальная мощность, тем большую силу тока и напряжение он способен выдержать.
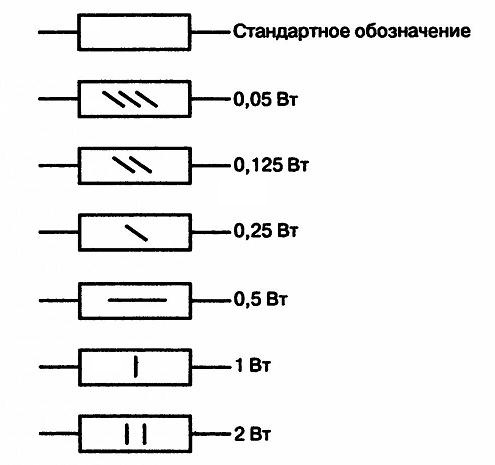
Резисторы выпускаются с мощностью рассеивания 0,125 Вт, 0,25 Вт, 0,5 Вт, 1 Вт, 2 Вт, 3 Вт, 5 Вт, 10 Вт, 25 Вт и более.
На резисторах, начиная с 1 Вт и выше, величина мощности указывается на корпусе в виде цифрового значения, тогда как малогабаритные резисторы приходится определять на «глаз».
С приобретением опыта определение мощности малогабаритных резисторов не вызывает никаких затруднений. На первое время в качестве ориентира для сравнения можно использовать обычную спичку. Более подробно прочитать про мощность и дополнительно посмотреть видеоролик можно в этой статье.
Однако с размерами есть небольшой нюанс, который надо учитывать при выполнении монтажа: габариты отечественных и зарубежных резисторов одинаковой мощности немного отличаются друг от друга — отечественные резисторы чуть больше своих зарубежных собратьев.
Резисторы можно разделить на две группы: резисторы постоянного сопротивления (постоянные резисторы) и резисторы переменного сопротивления (переменные резисторы).
2. Резисторы постоянного сопротивления (постоянные резисторы).
Постоянным считается резистор, сопротивление которого в процессе работы остается неизменным. Конструктивно такой резистор представляет собой керамическую трубку, на поверхность которой нанесен токопроводящий слой, обладающий определенным омическим сопротивлением. По краям трубки напрессованы металлические колпачки, к которым приварены выводы резистора, сделанные из облуженной медной проволоки. Сверху корпус резистора покрыт влагостойкой цветной эмалью.
Керамическую трубку называют резистивным элементом и в зависимости от типа токопроводящего слоя, нанесенного на поверхность, резисторы разделяются на непроволочные и проволочные.
2.1. Непроволочные резисторы.
Непроволочные резисторы используются для работы в электрических цепях постоянного и переменного тока, в которых протекают сравнительно небольшие токи нагрузки. Резистивный элемент резистора выполнен в виде тонкой полупроводящей пленки, нанесенной на керамическое основание.
Полупроводящая пленка называется резистивным слоем и изготавливается из пленки однородного вещества толщиной 0,1 – 10 мкм (микрометр) или из микрокомпозиций. Микрокомпозиции могут быть выполнены из углерода, металлов и их сплавов, из окислов и соединений металлов, а также в виде более толстой пленки (50 мкм), состоящей из размельченной смеси проводящего вещества.
В зависимости от состава резистивного слоя резисторы разделяются на углеродистые, металлопленочные (металлизированные), металлодиэлектрические, металлоокисные и полупроводниковые. Наиболее широкое применение получили металлопленочные и углеродистые композиционные постоянные резисторы. Из резисторов отечественного производства можно выделить МЛТ, ОМЛТ (металлизированный, лакированный эмалью, теплостойкий), ВС (углеродистые) и КИМ, ТВО (композиционные).
Непроволочные резисторы отличаются малыми размерами и массой, низкой стоимостью, возможностью применения на высоких частотах до 10 ГГц. Однако они недостаточно стабильны, так как их сопротивление зависит от температуры, влажности, приложенной нагрузки, продолжительности работы и т.п. Но все же положительные свойства непроволочных резисторов настолько значительны, что именно они получили наибольшее применение.
2.2. Проволочные резисторы.
Проволочные резисторы применяются в электрических цепях постоянного тока. При изготовлении резистора на его корпус в один или два слоя наматывается тонкая проволока, сделанная из никелина, нихрома, константана или других сплавов с высоким удельным электрическим сопротивлением. Высокое удельное сопротивление провода позволяет выполнить резистор с минимальным расходом материалов и небольших размеров. Диаметр применяемых проводов определяется плотностью тока, проходящего через резистор, технологическими параметрами, надежностью и стоимостью, и начинается с 0,03 – 0,05 мм.
Для защиты от механических или климатических воздействий и для закрепления витков резистор покрывается лаками и эмалями или герметизируется. Вид изоляции влияет на теплостойкость, электрическую прочность и наружный диаметр провода: чем больше диаметр провода, тем толще слой изоляции и тем выше электрическая прочность.
Наибольшее применение нашли провода в эмалевой изоляции ПЭ (эмаль), ПЭВ (высокопрочная эмаль), ПЭТВ (теплостойкая эмаль), ПЭТК (теплостойкая эмаль), достоинством которой является небольшая толщина при достаточно высокой электрической прочности. Распространенными резисторами большой мощности являются проволочные эмалированные резисторы типа ПЭВ, ПЭВТ, С5-35 и др.
По сравнению с непроволочными резисторами проволочные отличаются более высокой стабильностью. Они могут работать при более высоких температурах, выдерживают значительные перегрузки. Однако они сложнее в производстве, дороже и малопригодны для использования на частотах выше 1- 2 МГц, так как обладают высокой собственной емкостью и индуктивностью, которые проявляются уже на частотах в несколько килогерц.
Поэтому в основном их применяют в цепях постоянного тока или тока низких частот, там, где требуются высокие точности и стабильность работы, а также способность выдерживать значительные токи перегрузки вызывающие значительный перегрев резистора.
С появлением микроконтроллеров современная техника стала более функциональнее и одновременно с этим намного миниатюрнее. Использование микроконтроллеров позволило упростить электронные схемы и тем самым уменьшить потребление тока устройствами, что сделало возможным миниатюризировать элементную базу. На рисунке ниже показаны SMD резисторы, которые припаиваются на плату со стороны печатного монтажа.
3. Обозначение резисторов на принципиальных схемах.
На принципиальных схемах постоянные резисторы, независимо от их типа, изображают в виде прямоугольника, а выводы резистора изображают в виде линий, проведенных от боковых сторон прямоугольника. Такое обозначение принято повсеместно, однако в некоторых зарубежных схемах используется обозначение резистора в форме зубчатой линии (пилы).
Рядом с условным обозначением ставят латинскую букву «R» и порядковый номер резистора в схеме, а также указывают его номинальное сопротивление в единицах измерения Ом, кОм, МОм.
Значение сопротивления от 0 до 999 Ом обозначают в омах, но единицу измерения не ставят:
На некоторых зарубежных схемах для обозначения Ом ставят букву R:
Значение сопротивления от 1 до 999 кОм обозначают в килоомах с добавлением буквы «к»:
1,2к — 1,2 кОм
10к — 10 кОм
560к — 560 кОм
Значение сопротивления от 1000 кОм и больше обозначают в единицах мегаом с добавлением буквы «М»:
Резистор применяют согласно мощности, на которую он рассчитан, и которую может выдержать без риска быть испорченным при прохождении через него электрического тока. Поэтому на схемах внутри прямоугольника прописывают условные обозначения, указывающие мощность резистора: двойной косой чертой обозначают мощность 0,125 Вт; прямой чертой, расположенной вдоль значка резистора, обозначают мощность 0,5 Вт; римскими цифрами обозначается мощность от 1 Вт и выше.
4. Последовательное и параллельное соединение резисторов.
Очень часто возникает ситуация когда при конструировании какого-либо устройства под рукой не оказывается резистора с нужным сопротивлением, но зато есть резисторы с другими сопротивлениями. Здесь все очень просто. Зная расчет последовательного и параллельного соединения можно собрать резистор с любым номиналом.
При последовательном соединении резисторов их общее сопротивление Rобщ равно сумме всех сопротивлений резисторов, соединенных в эту цепь:
Rобщ = R1 + R2 + R3 + … + Rn
Например. Если R1 = 12 кОм, а R2 = 24 кОм, то их общее сопротивление Rобщ = 12 + 24 = 36 кОм.
При параллельном соединении резисторов их общее сопротивление уменьшается и всегда меньше сопротивления каждого отдельно взятого резистора:
Допустим, что R1 = 11 кОм, а R2 = 24 кОм, тогда их общее сопротивление будет равно:
И еще момент: при параллельном соединении двух резисторов с одинаковым сопротивлением, их общее сопротивление будет равно половине сопротивления каждого из них.
Из приведенных примеров понятно, что если хотят получить резистор с бо́льшим сопротивлением, то применяют последовательное соединение, а если с меньшим, то параллельное. А если остались вопросы, почитайте статью последовательное и параллельное соединение резисторов, в которой способы соединения рассказаны более подробно.
Ну и в дополнении к прочитанному посмотрите видеоролик о резисторах постоянного сопротивления.
Ну вот, в принципе и все, что хотел сказать о резисторе в целом и отдельно о резисторах постоянного сопротивления. Во второй части статьи мы познакомимся с резисторами переменного сопротивления.
Удачи!
Литература:
В. И. Галкин — «Начинающему радиолюбителю», 1989 г.
В. А. Волгов — «Детали и узлы радиоэлектронной аппаратуры», 1977 г.
В. Г. борисов — «Юный радиолюбитель», 1992 г.