какое самое большое число в мире цифрами
Самое большое число в мире, которое что-то обозначает
Миллион = 1 000 000 = 10⁶
Представить миллион чего-то мы тоже можем:
С миллионами чего-либо мы сталкиваемся довольно часто и так:
— миллион секунд — это всего-навсего 11,5 дней;
— миллион книг, поставленных друг на друга, не выйдет даже за пределы атмосферы Земли;
— очередь, из миллиона букв можно составить одну, достаточно большую, книгу (например, полная Библия состоит из более чем 2,5 миллионов букв).
— миллион горошин поместится в большом мешке, который в принципе можно будет даже приподнять, если вы не боитесь надорваться;
— миллион песчинок запросто поместится в пригоршне;
— миллион бактерий будет едва различим невооруженному глазу.
— человеческий волос, увеличенный в миллион раз, будет диаметром около 100 метров.
— здание в миллион этажей (если бы такое можно было построить) поднялось бы в высоту на 2,5 тысячи километров, — в 4 с лишним раза выше, чем летает телескоп Хаббла и большинство искусственных спутников Земли.
Миллиард = 1 000 000 000 = 10⁹
Представить миллиард чего-то мы тоже можем:
— миллиард молекул, поставленных «плечом к плечу», займут около 30 сантиметров (вообще, молекулы сильно различаются по своим размерам и для примера мы взяли молекулу воды, состоящую, как известно, из двух атомов водорода и одного атома кислорода);
— головной мозг человека состоит из 100 миллиардов нейронов и столько же, но только людей, жило на нашей планете за всю ее историю.
— если разделить расстояние от Земли до Луны на миллиард, то получится примерно 40 сантиметров. А если на тот же миллиард разделить расстояние от Земли до Солнца, то получится уже 150 метров, а это большой такой небоскреб высотой почти в половину Эйфелевой башни. Сама Земля, уменьшенная в миллиард раз, станет размером с виноградину, — и, кстати, тогда она превратится в черную дыру;
— космические аппараты «Вояджер», запущенные в 1977 году, пролетели почти по 20 миллиардов километров каждый;
— миллиард секунд — это 31,7 года, целое поколение.
— если увеличить атом водорода в миллиард раз, то его диаметр составит целых 10 сантиметров, хотя его ядро даже при таком увеличении все равно не разглядишь. В этом масштабе мельчайшие вирусы будут гигантами размером в несколько десятков, а то и сотен метров. И даже молекула ДНК будет шириной в целых 3 метра.
Триллион = 1 000 000 000 000 = 10¹²
— общая масса воздуха, который вдыхают все люди на нашей планете за 1 год, составляет около 6 триллионов килограмм;
— в океанах нашей планеты обитает около триллиона рыб;
— триллион секунд, как вы наверняка уже догадались, это в тысячу раз дольше, чем миллиард, — то есть 31 с лишним тысяча лет;
— примерно столько времени назад вымерли неандертальцы. Но это секунды. А вот через триллион лет случится нечто гораздо более интересное — в галактиках прекратят образовываться новые звезды;
— триллион километров — такое расстояние свет в вакууме проходит чуть больше чем за месяц;
— 42 триллиона километров — это расстояние до ближайшей к нам звезды (Проксимы Центавра);
— если мы возьмем триллион бактерий (допустим, у нас как-то получится их собрать всех вместе), то они займут объем одного кубика сахара. Примерно столько бактерий содержится на теле человека. А число клеток в нем — несколько десятков триллионов;
— во всех когда-либо отпечатанных книгах за всю историю книгопечатания около 100 триллионов букв;
— горстку из триллиона атомов даже не увидеть невооруженным взглядом, вот насколько они малы. Например, электрон. Он будет размером с горошину. А вот кварки, увеличенные в триллион раз, все еще не будут видны.
Квадриллион = 1 000 000 000 000 000 = 10¹⁵
— в теле человека (не только на коже, как в предыдущем абзаце) обитает до 1 квадриллиона бактерий, и их общий вес составляет около 2 килограмм;
— на нашей планете живет примерно квадриллион муравьев (да, их гораздо больше, чем людей, — примерно в 100 тысяч раз);
— пролететь квадриллион километров (а это примерно 100 световых лет), то можно посетить несколько ближайших к Земле звезд и вернуться обратно;
— через 200 квадриллионов секунд Солнце перейдет в стадию красного гиганта;
— еще самые мощные современные компьютеры выдают несколько десятков квадриллионов операций в секунду (петафлопсов).
Квинтиллион = 1 000 000 000 000 000 000 = 10¹⁸
— квинтиллион километров — это примерный диаметр нашей галактики, которая называется Млечный Путь;
— до нашей соседки — галактики Андромеды — 25 квинтиллионов;
— квинтиллион секунд — это время в 2 раза большее, чем то, которое прошло от Большого Взрыва и до сегодняшнего момента;
— именно столько кубометров воды есть на земле;
— 25-30 квинтиллионов молекул содержится в 1 куб.см воздуха при нормальной температуре и давлении (в основном, это молекулы азота – 78% и кислорода – 21%);
— масса всей атмосферы Земли — около 5 квинтиллионов килограмм;
— число возможных комбинаций кубика Рубика — 43 квинтиллиона с лишним.
Секстиллион = 1 000 000 000 000 000 000 000 = 10²¹
— столько атомов содержится в небольшом шарике из алюминия, диаметром в пару миллиметров;
— вес гидросферы Земли – полтора секстиллиона килограмм, а Луны около 70 секстиллионов;
— количество песчинок на всех пляжах Земли — несколько секстиллионов, хотя это сильно зависит от того, как и что именно мы считаем;
— размер видимой ее части — примерно 130 секстиллионов километров. Разумеется, такие расстояния никто в километрах не меряет, а использует для этого куда более подходящие световые годы и парсеки.
Септиллион = 1 000 000 000 000 000 000 000 000 = 10²⁴
— 6 септиллионов килограмм весит наша Земля;
— количество звезд в обозримой Вселенной — септиллион или совсем немного меньше;
— знаменитое число Авогадро, обозначающее количество молекул в одном моле вещества, составляет почти септиллион (более точное значение: 6 на 10²³ степени);
— 10 септиллионов молекул воды поместится в одном стакане. А если выложить в ряд 50 септиллионов маковых зерен, то такая цепочка протянется до Туманности Андромеды.
Октиллион = 1 000 000 000 000 000 000 000 000 000 = 10²⁷
Октиллион горошин займут такой же объем как планета Земля. Еще это число интересно тем, что если взять 5-10 октиллионов атомов, то из них можно составить человеческое тело.
Казнер знаменит тем, что придумал слова «гугол» и «гуголплекс», а также известно решение Казнера для вакуумного пространства-времени (1922), к которому, согласно с гипотезой Белинского — Лифшица — Халатникова, приближается асимптотически любое космологическое решение около сингулярности.
Число Скьюза. Записывается как 10 в степени 10 в степени 10 в степени 963. Обозначает верхний предел для математической задачи.
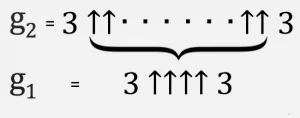
3|||3 это 3 с высотой столба степени 3 равной расстоянию от Земли до Марса. Количество троек в степени равняется 7.000.000.000.000. И заметьте, это не само число, а его степень! Математики обозначили его G1. Всего 5 троек из этой башни полностью покрывают гуголплекс, а первые 10 сантиметров ставят в тупик все существующие на Земле компьютеры. Дальше пустота и неведение. Далее идёт число G2, где количество стрелок равняется G1. Далее идёт G3, где количество стрелок равняется G2 и так далее. Всего таких чисел 64. G64 это и есть число Грэма. Записать его где либо невозможно, поэтому записывают формулой: G=f^64(4), где f(n)=3|^n3. (значок «^» обозначает степень: 1.000.000=10^6). Подсчитывать это бессмысленно. Число Грэма не поместится в тех самых 10 в степени 500 вселенных, даже если пронумеровать каждую частицу! Но мы всё же кое что знаем о нём. Вот последние 10 цифр этого числа: 2464195387. Первые цифры не знает никто. Возможно, через тысячи или десятки тысяч лет человечество всё-таки сможет его высчитать и оно станет элементарным и банальным.
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
“Я вижу скопления смутных чисел, которые скрывается там, в темноте, за небольшим пятном света, которое дает свеча разума. Они шепчутся друг с другом; сговариваясь кто знает о чем. Возможно, они нас не очень любят за захват их меньших братишек нашими умами. Или, возможно, они просто ведут однозначный числовой образ жизни, там, за пределами нашего понимания’’.
Дуглас Рэй
Каждого рано или поздно мучает вопрос, а какое же самое большое число. На вопрос ребенка можно ответить миллион. А что дальше? Триллион. А еще дальше? На самом деле, ответ на вопрос какие же самые большие числа прост. К самому большому числу просто стоит добавить единицу, как оно уже не будет самым большим. Процедуру эту можно продолжать до бесконечности. Т.е. получается нет самого большого числа в мире? Это бесконечность?
Существуют две системы наименования чисел — американская и английская.
Из английской системы в русский язык перешло только число миллиард (10 9 ), которое всё же было бы правильнее называть так, как его называют американцы — биллионом, так как у нас принята именно американская система. Но кто у нас в стране что-то делает по правилам! 😉 Кстати, иногда в русском языке употребляют и слово триллиард (можете сами в этом убедиться, запустив поиск в Гугле или Яндексе ) и означает оно, судя по всему, 1000 триллионов, т.е. квадриллион.
Кроме чисел, записанных при помощи латинских префиксов по американской или англйской системе, известны и так называемые внесистемные числа, т.е. числа, которые имеют свои собственные названия безо всяких латинских префиксов. Таких чисел существует несколько, но подробнее о них я расскажу чуть позже.
Вернемся к записи при помощи латинских числительных. Казалось бы, что ими можно записывать числа до бессконечности, но это не совсем так. Сейчас объясню почему. Посмотрим для начала как называются числа от 1 до 10 33 :
Самое маленькое такое число — это мириада (оно есть даже в словаре Даля), которое означает сотню сотен, то есть — 10 000. Слово это, правда, устарело и практически не используется, но любопытно, что широко используется слово «мириады», которое означает вовсе не определённое число, а бесчисленное, несчётное множество чего-либо. Считается, что слово мириада (англ. myriad) пришло в европейские языки из древнего Египта.
Гугол (от англ. googol) — это число десять в сотой степени, то есть единица со ста нулями. О «гуголе» впервые написал в 1938 году в статье «New Names in Mathematics» в январском номере журнала Scripta Mathematica американский математик Эдвард Каснер (Edward Kasner). По его словам, назвать «гуголом» большое число предложил его девятилетний племянник Милтон Сиротта (Milton Sirotta). Общеизвестным же это число стало благодаря, названной в честь него, поисковой машине Google. Обратите внимание, что «Google» — это торговая марка, а googol — число.

Эдвард Каснер (Edward Kasner).
Words of wisdom are spoken by children at least as often as by scientists. The name «googol» was invented by a child (Dr. Kasner’s nine-year-old nephew) who was asked to think up a name for a very big number, namely, 1 with a hundred zeros after it. He was very certain that this number was not infinite, and therefore equally certain that it had to have a name. At the same time that he suggested «googol» he gave a name for a still larger number: «Googolplex.» A googolplex is much larger than a googol, but is still finite, as the inventor of the name was quick to point out.
Mathematics and the Imagination (1940) by Kasner and James R. Newman.
Как вы понимаете чем больше в числе степеней, тем сложнее понять какое из чисел больше. Например, посмотрев на числа Скьюза, без специальных вычислений практически невозможно понять, какое из этих двух чисел больше. Таким образом, для сверхбольших чисел пользоваться степенями становится неудобно. Мало того, можно придумать такие числа (и они уже придуманы), когда степени степеней просто не влезают на страницу. Да, что на страницу! Они не влезут, даже в книгу, размером со всю Вселенную! В таком случае встаёт вопрос как же их записывать. Проблема, как вы понимаете разрешима, и математики разработали несколько принципов для записи таких чисел. Правда, каждый математик, кто задавался этой проблемой придумывал свой способ записи, что привело к существованию нескольких, не связанных друг с другом, способов для записи чисел — это нотации Кнута, Конвея, Стейнхауза и др.
Рассмотрим нотацию Хьюго Стенхауза (H. Steinhaus. Mathematical Snapshots, 3rd edn. 1983), которая довольно проста. Стейн хауз предложил записывать большие числа внутри геометрических фигур — треугольника, квадрата и круга:
Математик Лео Мозер доработал нотацию Стенхауза, которая была ограничена тем, что если требовалаось записывать числа много больше мегистона, возникали трудности и неудобства, так как приходилось рисовать множество кругов один внутри другого. Мозер предложил после квадратов рисовать не круги, а пятиугольники, затем шестиугольники и так далее. Также он предложил формальную запись для этих многоугольников, чтобы можно было записывать числа, не рисуя сложных рисунков. Нотация Мозера выглядит так:
Но и мозер не самое большое число. Самым большим числом, когда-либо применявшимся в математическом доказательстве, является предельная величина, известная как число Грэма (Graham’s number), впервые использованная в 1977 года в доказательстве одной оценки в теории Рамсея. Оно связано с бихроматическими гиперкубами и не может быть выражено без особой 64-уровневой системы специальных математических символов, введённых Кнутом в 1976 году.
К сожалению, число записанное в нотации Кнута нельзя перевести в запись по системе Мозера. Поэтому придётся объяснить и эту систему. В принципе в ней тоже нет ничего сложного. Дональд Кнут (да, да, это тот самый Кнут, который написал «Искусство программирования» и создал редактор TeX) придумал понятие сверхстепень, которое предложил записывать стрелками, направленными вверх:
В общем виде это выглядит так:
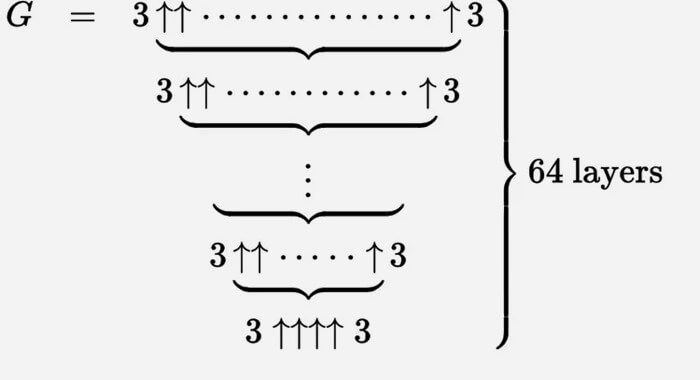
Думаю, что всё понятно, поэтому вернёмся к числу Грэма. Грэм предложил, так называемые G-числа:
Число G 63 стало называться числом Грэма (обозначается оно часто просто как G). Это число является самым большим известным в мире числом и занесёно даже в «Книгу рекордов Гинесса». А, вот тут лежит доказательство, что число Грэма больше числа Мозера.
Так есть числа больше, чем число Грэма? Есть, конечно, для начала есть число Грэма + 1. Что касается значащего числа… хорошо, есть некоторые дьявольски сложные области математики (в частности, области, известной как комбинаторика) и информатики, в которых встречаются числа даже большие, чем число Грэма. Но мы почти достигли предела того, что можно разумно и понятно объяснить.
Самое большое число в мире
Считается, что концепция чисел впервые возникла, когда доисторические люди начали использовать свои пальцы для подсчета чего-либо. С тех пор человечество прошло долгий путь. Теперь мы используем калькуляторы и компьютеры для подсчета самых больших чисел. И даже появились названия для чисел, которые настолько велики, что их с трудом можно представить.
Бесконечность счетных чисел
Казалось бы, ответ на вопрос о том, каково самое большое число в математике — очень прост. Бесконечность, верно? Но это не совсем правильно. Ведь бесконечность — вовсе не число, а концепция. Идея.
Бесконечность (infinitum) — это понятие, которое в переводе с латинского означает «без границ». Определение бесконечности в математике гласит, что независимо от того, насколько велико число, вы всегда можете добавить к нему 1, и оно станет больше.
Поэтому, строго говоря, не существует такого понятия, как самое большое число в мире. Можно лишь назвать наибольшее число, которому дали конкретное название.
Вот некоторые наиболее известные названия больших чисел:
| Число нулей | Название | Название на английском |
|---|---|---|
| 3 | тясяча | thousand |
| 6 | миллион | million |
| 9 | миллиард (биллион) | billion |
| 12 | триллион | trillion |
| 15 | квадриллион | quadrillion |
| 18 | квинтиллион | quintillion |
| 21 | секстиллион | sextillion |
| 24 | септиллион | septillion |
| 27 | октиллион | octillion |
| 30 | нониллион | nonillion |
| 33 | дециллион | decillion |
| 36 | ундециллион | undecillion |
| 39 | дуодециллион | duodecillion |
| 42 | тредециллион | tredecillion |
| 45 | кватуордециллион | quattuordecillion |
| 48 | квиндециллион | quindecillion |
| 51 | сексдециллион | sexdecillion |
| 54 | септендециллион | septendecillion |
| 57 | октодециллион | octodecillion |
| 60 | новемдециллион | novemdecillion |
| 63 | вигинтиллион | vigintillion |
| 66 | унвигинтиллион | unvigintillion |
| 69 | дуовигинтиллион | duovigintillion |
| 72 | тревигинтиллион | trevigintillion |
| 75 | кватуорвигинтиллион | quattuorvigintillion |
| 78 | квинвигинтиллион | quinvigintillion |
| 81 | сексвигинтиллион | sexvigintillion |
| 84 | септенвигинтиллион | septenvigintillion |
| 87 | октовигинтиллион | octovigintillion |
| 90 | новемвигинтиллион | novemvigintillion |
| 93 | тригинтиллион | trigintillion |
| 96 | унтригинтиллион | untrigintillion |
| 99 | дуотригинтиллион | duotrigintillion |
| 102 | третригинтиллион | trestrigintillion |
| 105 | кватортригинтиллион | quattuortrigintillion |
| 108 | квинтригинтиллион | quintrigintillion |
| 111 | секстригинтиллион | sextrigintillion |
| 114 | септентригинтиллион | septentrigintillion |
| 117 | октотригинтиллион | octotrigintillion |
| 120 | новемтригинтиллион | novemtrigintillion |
| 123 | квадрагинтиллион | quadragintillion |
| 126 | унквадрагинтиллион | unquadragintillion |
| 129 | дуоквадрагинтиллион | duoquadragintillion |
| 132 | треквадрагинтиллион | trequadragintillion |
| 135 | кваторквадрагинтиллион | quattuorquadragintillion |
| 138 | квинквадрагинтиллион | quinquadragintillion |
| 141 | сексквадрагинтиллион | sexquadragintillion |
| 144 | септенквадрагинтиллион | septenquadragintillion |
| 147 | октоквадрагинтиллион | octoquadragintillion |
| 150 | новемквадрагинтиллион | novemquadragintillion |
| 153 | квинквагинтиллион | quinquagintillion |
| 156 | унквинкагинтиллион | unquinquagintillion |
| 159 | дуоквинкагинтиллион | duoquinquagintillion |
| 162 | треквинкагинтиллион | trequinquagintillion |
| 165 | кваторквинкагинтиллион | quattuorquinquagintillion |
| 168 | квинквинкагинтиллион | quinquinquagintillion |
| 171 | сексквинкагинтиллион | sexquinquagintillion |
| 174 | септенквинкагинтиллион | septenquinquagintillion |
| 177 | октоквинкагинтиллион | octoquinquagintillion |
| 180 | новемквинкагинтиллион | novemquinquagintillion |
| 183 | сексагинтиллион | sexagintillion |
| 186 | унсексагинтиллион | unsexagintillion |
| 189 | дуосексагинтиллион | duosexagintillion |
| 192 | тресексагинтиллион | tresexagintillion |
| 195 | кваторсексагинтиллион | quattuorsexagintillion |
| 198 | квинсексагинтиллион | quinsexagintillion |
| 201 | секссексагинтиллион | sexsexagintillion |
| 204 | септенсексагинтиллион | septensexagintillion |
| 207 | октосексагинтиллион | octosexagintillion |
| 210 | новемсексагинтиллион | novemsexagintillion |
| 213 | септагинтиллион | septuagintillion |
| 216 | унсептагинтиллион | unseptuagintillion |
| 219 | дуосептагинтиллион | duoseptuagintillion |
| 222 | тресептагинтиллион | treseptuagintillion |
| 225 | кваторсептагинтиллион | quattuorseptuagintillion |
| 228 | квинсептагинтиллион | quinseptuagintillion |
| 231 | секссептагинтиллион | sexseptuagintillion |
| 234 | септенсептагинтиллион | septenseptuagintillion |
| 237 | октосептагинтиллион | octoseptuagintillion |
| 240 | новемсептагинтиллион | novemseptuagintillion |
| 243 | октогинтиллион | octogintillion |
| 246 | уноктогинтиллион | unoctogintillion |
| 249 | дуооктогинтиллион | duooctogintillion |
| 252 | треоктогинтиллион | treoctogintillion |
| 255 | кватороктогинтиллион | quattuoroctogintillion |
| 258 | квиноктогинтиллион | quinoctogintillion |
| 261 | сексоктогинтиллион | sexoctogintillion |
| 264 | септоктогинтиллион | septoctogintillion |
| 267 | октооктогинтиллион | octooctogintillion |
| 270 | новемоктогинтиллион | novemoctogintillion |
| 273 | нонагинтиллион | nonagintillion |
| 276 | уннонагинтиллион | unnonagintillion |
| 279 | дуононагинтиллион | duononagintillion |
| 282 | тренонагинтиллион | trenonagintillion |
| 285 | кваторнонагинтиллион | quattuornonagintillion |
| 288 | квиннонагинтиллион | quinnonagintillion |
| 291 | секснонагинтиллион | sexnonagintillion |
| 294 | септеннонагинтиллион | septennonagintillion |
| 297 | октононагинтиллион | octononagintillion |
| 300 | новемнонагинтиллион | novemnonagintillion |
| 303 | центиллион | centillion |
Как называется самое большое простое число

Какое самое большое число в мире

Кратко об этой теории: представим себе N-мерный куб, его вершины в случайном порядке соединены красными или синими отрезками-линиями. А наша задача — понять, до какого значения N возможно (если по-разному закрашивать ребра куба), избежать ситуации, при которой одна плоскость в кубе будет окрашена одним цветом. То есть у нас не должен получиться одноцветный «конвертик».
Математики позакрашивали кубик и так и эдак, получилось, что до шестимерного куба можно исхитриться и сделать, чтобы линии одного цвета, соединяющие четыре вершины, не лежали в одной плоскости. А вот с семимерным, как выяснили Грэм и Ротшильд, такой фокус уже не провернешь. И с восьмимерным. И… «и так далее», которое, впрочем, не бесконечно, а заканчивается фантастически гигантским числом. Вот его-то и именуют числом Грэма. Кстати, в настоящее время решение Грэма и Ротшильда устарело. Математики выяснили, что 6-7-8-9-10-11-12-мерные кубы все же можно покрасить без «конвертов». Но где-то в промежутке между 13 и числом Грэма гарантированно есть число выше которого «конверты» в любом случае будут.
Число Грэма получило всемирное признание в 1977 году, когда известный популяризатор науки Мартин Гарднер написал об этом в Scientific American.
И хотя с тех пор в математической науке были и другие кандидаты на титул самого большого числа, «детище» Грэма является самым распиаренным и общеизвестным. И если вы слышали про «гугольное семейство»:
Любопытно, что придумав гугол американский математик Эдвард Казнер хотел показать студентам разницу между невероятно большим числом и бесконечностью. Тогда число Грэма может просто «взорвать мозг».
Возможно ли представить и записать число за гранью понимания
Математики не смогут назвать вам точное количество цифр в числе Грэма, не говоря уже о том, чтобы досчитать до него. Известны лишь последние 50 цифр самого большого числа в мире — это …03222348723967018485186439059104575627262464195387.
А вот цифры, с которых начинается G64 неизвестны, и вряд ли когда-либо будут.
Давайте сравним трех монстров: гугол, гуголплекс и число Грэма.
Теперь представьте, что в какой-то момент вы берете одну песчинку, чтобы рассмотреть ее под мощным микроскопом. И видите, что на самом деле это не единственное зерно, а 10 миллиардов микроскопических зерен, а все вместе они размером с песчинку. Если бы это было так для каждой отдельной песчинки в этой гипотетической вселенной, то общее количество этих микроскопических зерен было бы гуголом.
Как записать G64 с помощью метода Кнута
В 1976 году американский ученый Дональд Кнут предложил понятие сверхстепеней или нотацию Кнута. Это метод, позволяющий при помощи стрелочек, направленных вверх, записывать очень большие числа. Возведение в степень обозначается одной стрелкой вверх: ↑.
Вот как выглядит эта нотация: a ↑ b = ab = a × a × a × …, и так b раз.
Важной особенностью стрелок вверх является то, что они растут очень быстро. Экспонентация растет гораздо быстрее, чем умножение. 2 × 10 — это всего лишь 20, но 2↑10 = 1024. Таким же образом, каждый новый уровень стрелок растет намного быстрее, чем предыдущий уровень.
Если мысленно представить себе степенную башню из троек 3↑↑↑4 то получится конструкция, размером от Земли до Марса. А ведь мы еще даже не дошли до «нижней ступеньки», ведущей нас к числу Грэма.
Мы можем описать число Грэма огромным набором этих стрелок вверх.
Проще всего думать об этом как об итерационном процессе. Мы начинаем снизу с g 1 = 3 ↑↑↑↑ 3, а затем создаем вторую строку (назовем ее g 2) с g 1 стрелками между тройками.
Тогда g 3 — это две тройки, разделенные g 2 стрелками вверх и так далее, пока g 64 с g 63 стрелками между тройками не будет числом Грэма.
Если выбрать продолжительность жизни, равную числу Грэма вместо бессмертия, то результат будет практически одинаков. Даже если предположить, что условия во Вселенной, в Солнечной системе и на Земле вечно останутся неизменными, человеческий мозг никак не мог бы выдержать столь длинный промежуток времени без пагубных изменений.
 masterok
masterok