какое распределение имеет случайная величина
Содержание:
Законы распределения:
Распределение случайных переменных: Каждая из случайных переменных имеет ряд возможных значений, могущих возникнуть с определенной вероятностью.
Случайные переменные величины могут носить прерывный (дискретный) и непрерывный характер. Возможные значения прерывной случайной переменной отделены друг от друга конечными интервалами. Возможные значения непрерывной случайной переменной не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
Примерами прерывных случайных переменных могут служить:
Примеры непрерывных случайных переменных:
Если перечислить все возможные значения случайной переменной и указать вероятности этих значений, то получится распределение случайной переменной. Распределение случайной переменной указывает на соотношение между отдельными значениями случайной величины и их вероятностями.
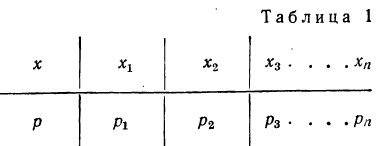
Распределение случайной переменной будет задано законом распределения, если точно указать, какой вероятностью обладает каждое значение случайной переменной.
Такая таблица называется также рядом распределения случайной переменной.
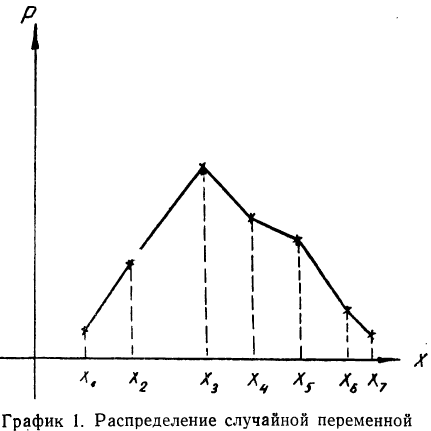
Для наглядности ряд распределения изображают графически, откладывая на прямоугольной системе координат по оси абсцисс возможные значения случайной переменной, а по оси ординат — их вероятности. В результате графического изображения получается многоугольник или полигон распределения (график 1). Многоугольник распределения является одной из форм закона распределения.
Функция распределения
Ряд распределения является исчерпывающей характеристикой прерывной случайной перемен-
Вероятность того, что Х
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Какое распределение имеет случайная величина
1. Формирование представление о случайной величине, дискретных и непрерывных случайных величинах.
2. Знакомство с законом распределения дискретной случайной величины, функцией распределения и плотностью распределения непрерывной случайной величины, числовых характеристиках случайных величин.
1. Виды случайных величин.
2. Закон распределения дискретной случайной величины.
3. Функция распределения вероятностей случайной величины.
4. Плотность распределения вероятностей непрерывной случайной величины.
5. Математическое ожидание.
6. Дисперсия и среднеквадратическое отклонение.
1. Виды случайных величин.
Случайной величиной называется такая величина, которая случайно принимает какое-то значение из множества возможных значений.
По множеству возможных значений различают дискретные и непрерывные случайные величины.
Дискретными называются случайные величины, значениями которых являются только отдельные точки числовой оси. (Число их может быть как конечно, так и бесконечно).
Пример: Число родившихся девочек среди ста новорожденных за последний месяц- это дискретная случайная величина, которая может принимать значения 1,2,3,…
Непрерывными называются случайные величины, которые могут принимать все значения из некоторого числового промежутка.
2. Закон распределения дискретной случайной величины.
Закон распределения дискретной случайной величины— это соответствие между возможными значениями случайной величины и их вероятностями.
Закон распределения можно задать таблично, аналитически, графически.
При задании закона распределения таблично, в первую строку таблицы вносятся возможные значения случайно величины, а во вторую- их вероятности.
Пример: Монету подбросили 3 раза. Запишите закон распределения числа выпадения «герба».
Возможные значения данной случайной величины: 0, 1, 2, 3.
Найдем вероятность того, что «герб» не появится (0 раз).
Найдем вероятность того, что «герб» появится 1 раз.
Найдем вероятность того, что «герб» появится 2 раза.
Найдем вероятность того, что «герб» появится 3 раза.
Тогда закон распределения данной дискретной случайной величины можно представить таблицей:
Для наглядности закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки с координатами (xi ; pi), а затем соединяют их отрезками прямых. Полученная фигура называется многоугольником распределения.
Однако, такой способ задания (перечисление всех возможных значений случайной величины и их вероятностей) не подходит для непрерывных случайных величин. Составить перечень их возможных значений невозможно.
3. Функция распределения вероятностей случайной величины.
Дадим новый способ задания любых типов случайных величин. С этой целью введем функцию распределения вероятностей случайной величины.
Функцией распределения случайной величины называют функцию F ( x ), определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньшее х, т.е. F ( x ) P ( X x ).
Геометрически это равенство можно истолковать так: F ( x ) –есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Иногда вместо термина «функция распределения» используется термин «интегральная функция».
Свойства функции распределения:
Следствие 1: Вероятность того, что случайная величина примет значение, заключенное в интервале (а; b ), равна приращению функции распределения на этом интервале:
Пример: Случайная величина Х задана функцией распределения:
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0; 2).
Следствие: Если возможные значения непрерывной случайной величины распределены на всей числовой оси, то справедливы следующие предельные соотношения:
Рассмотренные выше свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.
График расположен в полосе, ограниченной прямыми у=0, у=1 (1 свойство).
4. При возрастании значения х в интервале ( a ; b ), в котором заключены все возможные значения случайной величины, график растет вверх (2 свойство).
5. При ординаты графика равны 0, при ординаты графика равны 1 (3 свойство).
Замечание: График функции распределения дискретной случайной величины имеет ступенчатый вид.
Пример: Дискретная случайная величина Х задана таблицей распределения:
Найдите функцию распределения и постройте ее график.
Итак, функция распределения имеет следующий вид:
4. Плотность распределения вероятностей непрерывной случайной величины.
Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (дифференциальной функцией).
Плотность распределения вероятностей непрерывной случайной величины Х называют функцию f ( x )- первую производную от функции распределения F ( x ).
Пример: Задана плотность вероятностей случайной величины Х.
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).
Свойства плотности распределения вероятностей:
Свойство 1: Плотность распределения- неотрицательная функция: f ( x ) > 0.
Часто, для того чтобы характеризовать случайную величину используют числа, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины. К числу важнейших числовых характеристик относятся математическое ожидание и дисперсия.
5. Математическое ожидание.
Математическое ожидание приближенно равно среднему значению случайной величины. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и следовательно стреляет лучше.
Пример: Найдите математическое ожидание, зная закон распределения дискретной случайной величины.
Основные законы распределения
1.Биномиальный закон распределения.
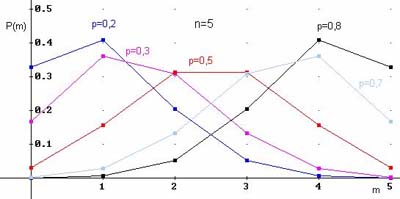
Биномиальный закон распределения описывает вероятность наступления события А m раз в n независимых испытаниях, при условии, что вероятность р наступления события А в каждом испытании постоянна.
Например, отдел продаж магазина бытовой техники в среднем получает один заказ на покупку телевизоров из 10 звонков. Составить закон распределения вероятностей на покупку m телевизоров. Построить полигон распределения вероятностей.
2.Геометрическое распределение.
Геометрическое распределение случайной величины имеет следующий вид:
Пример. В компанию по ремонту бытовой техники поступила партия из 10 запасных блоков для стиральных машин. Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей.
3.Гипергеометрическое распределение.
Гипергеометрическое распределение случайной величины имеет следующий вид:
Из таблицы видно, что вероятность угадывания одного числа m=1 выше, чем при m=0. Однако затем вероятность начинает быстро снижаться. Таким образом, вероятность угадывания 4-х чисел уже составляет менее 0,005, а 5-ти ничтожно мала.
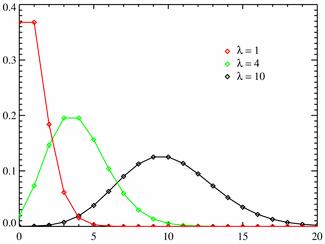
4.Закон распределения Пуассона.
Случайная величина Х имеет распределение Пуассона, если закон ее распределения имеет вид:
Из условия имеем: m=100, λ 1 =8, λ 2 =6, λ 3 =4 ( ≤10 )
(таблица дана не полностью)
Если n достаточно большое и стремится к бесконечности, а значение p стремится к нулю, так что произведение np стремится к постоянному числу, то данный закон является приближением к биномиальному закону распределения. Из графика видно, что чем больше вероятность р, тем ближе кривая расположена к оси m, т.е. более пологая. (Рис.4)
Необходимо отметить, что биномиальный, геометрический, гипергеометрический и закон распределения Пуассона выражают распределение вероятностей дискретной случайной величины.
5.Равномерный закон распределения.
Если плотность вероятности ϕ(х) есть величина постоянная на определенном промежутке [a,b], то закон распределения называется равномерным. На рис.5 изображены графики функции распределения вероятностей и плотность вероятности равномерного закона распределения.
6.Нормальный закон распределения (закон Гаусса).
Среди законов распределения непрерывных случайных величин наиболее распрастраненным является нормальный закон распределения. Случайная величина распределена по нормальному закону распределения, если ее плотность вероятности имеет вид:
График плотности вероятности случайной величины, имеющей нормальный закон распределения, симметричен относительно прямой х=а, т.е х равному математическому ожиданию. Таким образом, если х=а, то кривая имеет максимум равный:
При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (Рис.6) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины.
Функция, которая выражает распределение случайной величины на интервале (-∞,х), и имеющая нормальный закон распределения, выражается через функцию Лапласа по следующей формуле:
7.Показательный закон распределения.
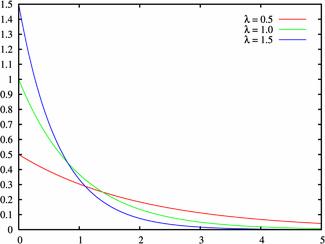
Закон распределения случайной величины Х называется показательным (или экспоненциальным), если плотность вероятности имеет вид:
График плотности вероятности с параметрами
λ = 2, λ = 4, λ =6 изображен на рис.8
Функция распределения случайной величины Х, которая имеет показательное распределение, имеет вид:
График функции изображен на рис.9
Если функцию распределения случайной величины выразить через плотность вероятности при х ≥ а, то она примет вид:
8.Логарифмически-нормальное распределение.
Если логарифм непрерывной случайной величины изменяется по нормальному закону, то случайная величина имеет логарифмически-нормальное распределение. Функция логаривмически-нормального распределения имеет вид.
Из графика видно, что чем меньше σ и больше математическое ожидание а, тем кривая становится более пологая и больше стремится к симметрии. Данный закон, чаще всего, используется для описания распределения поступления денежных средств (доходов), банковских вкладов, износа основных средств и т.д. (Рис.10)
9. χ ² распределение
Сумма квадратов k независимых случайных величин, которые распределены по нормальному закону, называется χ ² распределением.
χ ² распределение имеет вид:
Плотность вероятности случайной величины, распределенной по распределению χ ² имеет вид:
Из графика видно, что чем больше n=k, тем кривая стремиться к нормальному распределению. Рис.11.
Распределение непрерывной случайной величины называется распределением Стьюдента, если оно имеет вид:
Плотность вероятности распределения Стьюдента имеет вид:
На рис.12 изображена плотность вероятности распределения Стьюдента. Из графика можно увидеть, что чем больше k, тем больше кривая приближается к нормальному распределению.
11. Распределение Фишера-Снедекора.
Распределение случайной величины Фишера-Снедекора имеет вид:
Плотность вероятности случайной величины имеет вид:
При стремлении n к бесконечности распределение Фишера-Снедекора стремится к нормальному закону распределения.(Рис.13)
Формулы: законы распределения случайных величин
В данном разделе вы найдете формулы по теории вероятностей, описывающие законы распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, экспоненциальный, равномерный, нормальный.
Каталог формул по теории вероятности онлайн
Законы распределения на этой странице
Дискретные случайные величины
Биномиальное распределение ДСВ
| $x_k$ | 0 | 1 | . | k | . | n |
| $p_k$ | $q^n$ | $n\cdot p \cdot q^ | $C_n^k \cdot p^k \cdot q^ | $p^n$ |
Здесь вероятности находятся по формуле Бернулли:
Числовые характеристики биномиального распределения:
Пуассоновское распределение ДСВ
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Ряд распределения по закону Пуассона имеет вид:
| $x_k$ | 0 | 1 | . | k | . |
| $p_k$ | $e^<-\lambda>$ | $\lambda e^<-\lambda>$ | . | $\frac<\lambda^k> | . |
Вероятности вычисляются по формуле Пуассона:
Числовые характеристики для распределения Пуассона:
Геометрическое распределение ДСВ
Формула для вероятностей:
Ряд распределения геометрического закона:
| $x_k$ | 0 | 1 | 2 | . | k | . |
| $p_k$ | $p$ | $q\cdot p$ | $q^2 \cdot p$ | . | $q^k \cdot p$ | . |
Гипергеометрическое распределение ДСВ
$$M(X)=\frac
Непрерывные случайные величины
Показательное распределение НСВ
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Числовые характеристики можно найти по формулам:
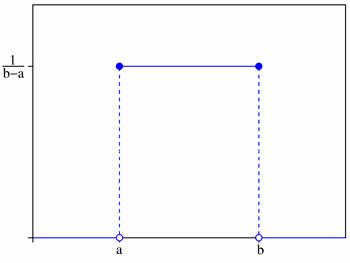
Равномерное распределение НСВ
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.
Числовые характеристики равномерно распределенной случайной величины:
График плотности вероятностей:
Нормальное распределение или распределение Гаусса НСВ
Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.
Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
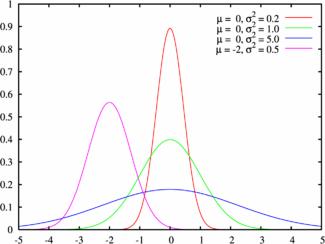
Числовые характеристики для нормального распределения:
Пример графика плотности распределения для различных значений среднего и СКО:
Функция Лапласа определяется как:
Решенные задачи по теории вероятностей
Ищете готовые задачи по теории вероятностей? Посмотрите в решебнике:
Какое распределение имеет случайная величина
тБУРТЕДЕМЕОЙС УМХЮБКОЩИ ЧЕМЙЮЙО УХФШ ПУОПЧОЩЕ ПВЯЕЛФЩ ЙЪХЮЕОЙС Ч ФЕПТЙЙ ЧЕТПСФОПУФЕК. нЩ ОЕ ВХДЕН, ЛБЛ РТБЧЙМП, ЙОФЕТЕУПЧБФШУС ФЕН, ЙЪ ЛБЛПЗП НОПЦЕУФЧБ ДЕКУФЧХЕФ ЖХОЛГЙС Й ЛБЛЙН ЙНЕООП ЬМЕНЕОФБТОЩН ЙУИПДБН УПРПУФБЧМСЕФ УЧПЙ ЧПЪНПЦОЩЕ ЪОБЮЕОЙС. оБУ ЮБЭЕ ВХДЕФ ЙОФЕТЕУПЧБФШ ФП, ОБ НОПЦЕУФЧЕ ЛБЛПК ЧЕТПСФОПУФЙ ЬФЙ ЪОБЮЕОЙС РТЙОЙНБАФУС. рТЙЧЕДЈН ОЕУЛПМШЛП РТЙНЕТПЧ УПЧЕТЫЕООП ТБЪОЩИ УМХЮБКОЩИ ЧЕМЙЮЙО, ЙНЕАЭЙИ ПДОП Й ФП ЦЕ ТБУРТЕДЕМЕОЙЕ ( ПДЙОБЛПЧП ТБУРТЕДЕМЈООЩИ ).
=1, ЕУМЙ = ЗЕТВ, Й =0, ЕУМЙ = ТЕЫЛБ;
=0, ЕУМЙ = ЗЕТВ, Й =1, ЕУМЙ = ТЕЫЛБ.
2. фПЮЛБ ОБХДБЮХ ВТПУБЕФУС ОБ ПФТЕЪПЛ [0, 1]. ч ЬФПН УМХЮБЕ ЕУФШ ПФТЕЪПЛ [0, 1] У УЙЗНБ-БМЗЕВТПК ВПТЕМЕЧУЛЙИ РПДНОПЦЕУФЧ Й НЕТПК мЕВЕЗБ. рТЕДМБЗБА ЮЙФБФЕМА ХВЕДЙФШУС, ЮФП ДЧЕ УПЧЕТЫЕООП ТБЪОЩЕ ЖХОЛГЙЙ: Й (ТБУУФПСОЙС ДП ХРБЧЫЕК ФПЮЛЙ ПФ МЕЧПЗП Й ПФ РТБЧПЗП ЛПОГПЧ ПФТЕЪЛБ УППФЧЕФУФЧЕООП) ПВМБДБАФ ПДЙОБЛПЧЩНЙ ЧЕТПСФОПУФСНЙ РТЙОЙНБФШ ЪОБЮЕОЙС ЧОХФТЙ МАВЩИ ВПТЕМЕЧУЛЙИ НОПЦЕУФЧ (ЧЕТПСФОПУФЙ, ТБЧОЩЕ НЕТЕ мЕВЕЗБ РЕТЕУЕЮЕОЙС НОПЦЕУФЧ Й [0, 1]). фБЛЙН ПВТБЪПН, ЬФЙ УМХЮБКОЩЕ ЧЕМЙЮЙОЩ УОПЧБ ПДЙОБЛПЧП ТБУРТЕДЕМЕОЩ, ОП ОЕ ПДЙОБЛПЧЩ: ЙИ ЪОБЮЕОЙС УПЧРБДБАФ МЙЫШ РТЙ ПДОПН ЬМЕНЕОФБТОПН ЙУИПДЕ = 0.5 ( ОБТЙУПЧБФШ ЗТБЖЙЛЙ ЖХОЛГЙК Й ).
пРЙЫЕН ТБЪМЙЮОЩЕ ФЙРЩ ТБУРТЕДЕМЕОЙК УМХЮБКОЩИ ЧЕМЙЮЙО. чУС ЧЕТПСФОПУФОБС НБУУБ НПЦЕФ ВЩФШ УПУТЕДПФПЮЕОБ Ч ОЕУЛПМШЛЙИ ФПЮЛБИ РТСНПК, НПЦЕФ ВЩФШ «ТБЪНБЪБОБ» РП ОЕЛПФПТПНХ ЙОФЕТЧБМХ ЙМЙ РП ЧУЕК РТСНПК. ч ЪБЧЙУЙНПУФЙ ПФ ФЙРБ НОПЦЕУФЧБ, ОБ ЛПФПТПН УПУТЕДПФПЮЕОБ ЧУС ЕДЙОЙЮОБС ЧЕТПСФОПУФОБС НБУУБ, ТБУРТЕДЕМЕОЙС ДЕМСФ ОБ ДЙУЛТЕФОЩЕ, БВУПМАФОП ОЕРТЕТЩЧОЩЕ, УЙОЗХМСТОЩЕ Й ЙИ УНЕУЙ.
еУМЙ УМХЮБКОБС ЧЕМЙЮЙОБ ЙНЕЕФ ДЙУЛТЕФОПЕ ТБУРТЕДЕМЕОЙЕ, ФП ДМС МАВПЗП
дЙУЛТЕФОПЕ ТБУРТЕДЕМЕОЙЕ ХДПВОП ЪБДБЧБФШ УМЕДХАЭЕК ФБВМЙГЕК, Ч ЛПФПТПК :
фПЗДБ ДМС МАВПЗП ЧЩРПМОЕОП:
оБЛПОЕГ, ТБУРТЕДЕМЕОЙЕ НПЦЕФ ВЩФШ ЧЩРХЛМПК МЙОЕКОПК ЛПНВЙОБГЙЕК ДЙУЛТЕФОПЗП, БВУПМАФОП ОЕРТЕТЩЧОПЗП Й УЙОЗХМСТОПЗП ТБУРТЕДЕМЕОЙК.
ч УЙМХ ОЕЪБЧЙУЙНПУФЙ УПВЩФЙК РПД ЪОБЛПН ЛБЦДПК ЙЪ ЧЕТПСФОПУФЕК,