какое наибольшее число ребер куба может пересечь одна плоскость четыре пять три шесть
Тест №12: «Пересечение многогранника плоскостью»
1. Какая фигура получается в сечении данного многогранника плоскостью α?
2. Какая фигура получается в сечении данной призмы плоскости β?
3. Какая плоскость образует в сечении многоугольник с наибольшим количеством вершин?
1. 
2. 
3. 
4. 
4. Какая фигура образуется в сечении треугольной призмы, если заданная плоскость пересекает два боковых ребра и треугольник основания?
Пятиугольник Треугольник Четырехугольник Шестиугольник
5. Какая фигура образуется в сечении четырехугольной пирамиды, если заданная плоскость пересекает три боковых ребра и четырехугольник основания?
Треугольник Пятиугольник Шестиугольник Четырехугольник
6. Какое наибольшее количество ребер куба может пересечь одна плоскость?
Четыре Семь Пять Шесть
7. 
Которая из плоскостей пересекает куб, образуя в сечении четырехугольник?
1. 1.
2. 2.
3. 3.
4. 4.
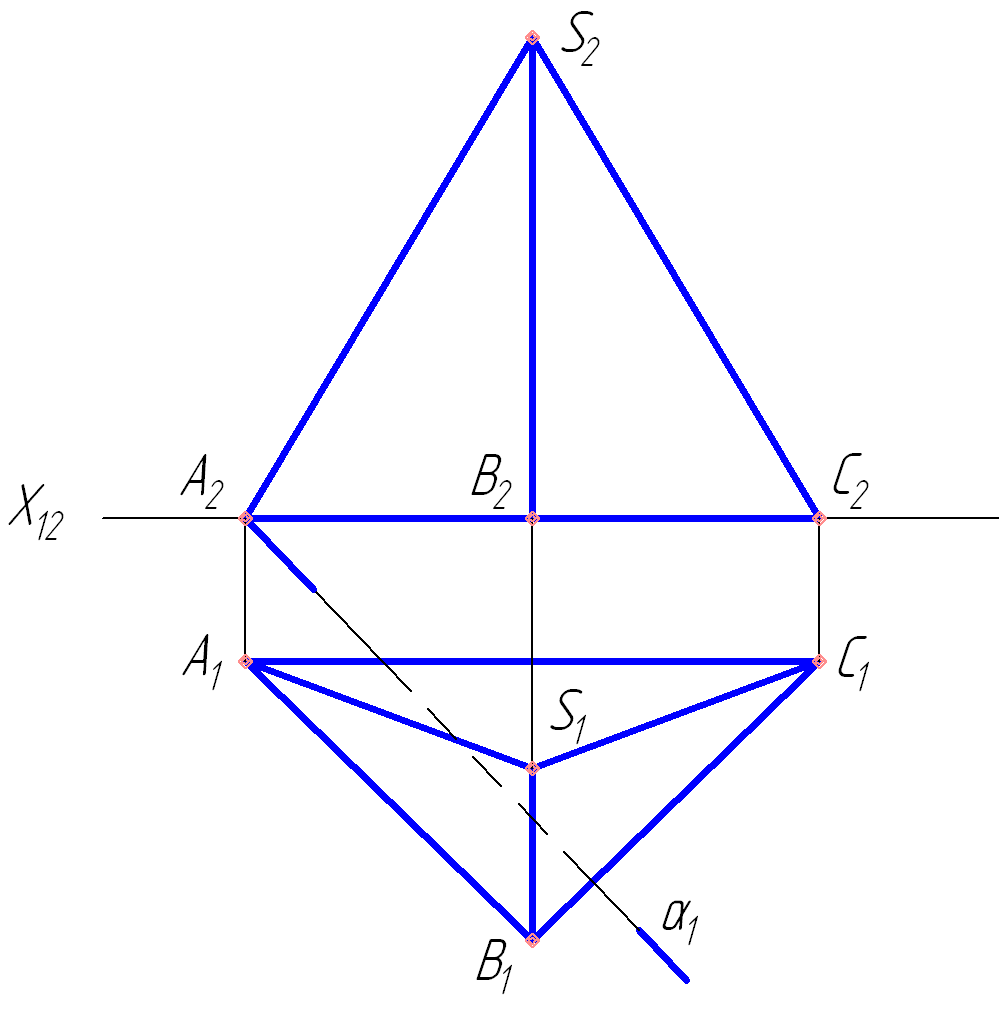
8. Построить сечение пирамиды плоскостью α (α1). Определить видимость.
8.1. Что представляют собой боковые грани пирамиды?
А – ве ртикально-проецирующие плоскости;
В – горизонтально-проецирующие плоскости;
С – плоскости общего положения.
8.2. На какой плоскости проекций располагается основание пирамиды?
8.3. Проецируются ли боковые ребра пирамиды на плоскости проекций П1 или П2 в истинную величину?
8.4. Проецируется ли основание пирамиды на плоскость П1 в истинную величину?
8.5. Какое из боковых ребер пирамиды является профильной прямой?
8.6. Как называется плоскость α1?
8.7. Где располагается горизонтальная проекция линии пересечения пирамиды плоскостью?
В – на горизонтальном следе плоскости α1.
8.8. Какую геометрическую плоскую фигуру будет представлять собой сечение пирамиды плоскостью α1?
8.9. Проецируется ли вертикальная проекция линии пересечения пирамиды плоскостью α1 в истинную величину?
Какое наибольшее число ребер куба может пересечь одна плоскость четыре пять три шесть
В кубе ABCDA1B1C1D1 все рёбра равны 7. На его ребре BB1 отмечена точка K так. что KB = 4. Через точки K и C1 проведена плоскость α, параллельная прямой BD1.
б) Найдите объём большей из двух частей куба, на которые он делится плоскостью α.
Это задание ещё не решено, приводим решение прототипа.
Водолазный колокол, содержащий υ = 2 моля воздуха при давлении p1 = 1,75 атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления p2. Работа, совершаемая водой при сжатии воздуха, определяется выражением 
где 
— постоянная, T = 300 K — температура воздуха. Найдите, какое давление p2 (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 15 960 Дж.
Задача сводится к решению уравнения 
:
Проверочная работа «13 задание ПРОФИЛЬ ЕГЭ математика»
Ищем педагогов в команду «Инфоурок»
ПРОФИЛЬ ЕГЭ математика
1. Дана правильная четырехугольная пирамида SABCD. Плоскость α параллельна прямой АС, проходит через точку В и середину высоты пирамиды.
а) Докажите, что плоскость α делит ребро SD в отношении 2 : 1, считая от точки D.
б) Найдите синус угла между плоскостью α и плоскостью ASC, если угол SAC равен 30°.
2. Боковое ребро правильной треугольной пирамиды SABC равно 6, а косинус угла ASB при вершине боковой грани равен 
Точка M — середина ребра SC, точка 
— середина ребра AC.
а) Докажите, что угол между прямыми BM и SA равен углу BMN.
б) Найдите косинус угла между прямыми BM и SA.
3. В основании правильной пирамиды PABCD лежит квадрат ABCD со стороной 9. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды.
4. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB = 4 и диагональю BD = 7. Все боковые рёбра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF = BE = 3.
б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.
5. В конус, радиус основания которого равен 6, вписан шар радиуса 3.
а) Изобразите осевое сечение комбинации этих тел.
б) Найдите отношение площади полной поверхности конуса к площади поверхности шара.
6. В пирамиде SABC в основании лежит правильный треугольник ABC со стороной 
Точка O — основание высоты пирамиды, проведённой из вершины S.
а) Докажите, что точка O лежит вне треугольника ABC.
б) Найдите объём четырёхугольной пирамиды SABCO.
7. Точка M середина ребра AB правильного тетраэдра DABC.
а) Докажите, что ортогональная проекция точки M на плоскость ACD лежит на медиане AP грани ACD.
б) Найдите угол между прямой DM и плоскостью ACD.
8. Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Грань ACC1A1 является квадратом.
а) Докажите, что прямые CA1 и AB1 перпендикулярны.
б) Найдите расстояние между прямыми CA1 и AB1, если AC = 4, BC = 7.
9. Длины всех ребер правильной четырёхугольной пирамиды PABCD с вершиной P равны между собой. Точка M — середина бокового ребра пирамиды AP.
а) Докажите, что плоскость, проходящая через точки B и M и перпендикулярная плоскости BDP, делит высоту пирамиды пополам.
б) Найдите угол между прямой BM и плоскостью BDP.
а) Докажите, что B1KLM — правильная пирамида.
ПРОФИЛЬ ЕГЭ математика
1. Точки A, B и C лежат на окружности основания конуса с вершиной S, причём A и C диаметрально противоположны. Точка M — середина BC.
а) Докажите, что прямая SM образует с плоскостью ABC такой же угол, как и прямая AB с плоскостью SBC.
б) Найдите угол между прямой SA и плоскостью SBC, если AB = 4, BC = 6 и 
2. В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB = 3. Через точки K и C1 построена плоскость α, параллельная прямой BD1.
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.
3. В основании четырехугольной пирамиды SАВСD лежит параллелограмм АВСD c центром О. Точка N — середина ребра SC, точка L — середина ребра SA.
а) Докажите, что плоскость BNL делит ребро SD в отношении 1 : 2, считая от вершины S.
б) Найдите угол между плоскостями BNL и АВС, если пирамида правильная, SA = 8, а тангенс угла между боковым ребром и плоскостью основания пирамиды равен 
4. Основание ABCD призмы 
— трапеция с основаниями AB = 2CD.
а) Докажите 
проходит через середину бокового ребра 
б) Найдите угол между боковым ребром 
и этой плоскостью, если призма прямая, трапеция ABCD прямоугольная с прямым углом при вершине B, а BC = CD и 
5. В правильной треугольной пирамиде SABC сторона основания AB равна 9, а боковое ребро SA = 6. На рёбрах AB и SC отмечены точки K и M соответственно, причём AK : KB = SM : MC = 2 : 7. Плоскость α содержит прямую KM и параллельна прямой SA.
а) Докажите, что плоскость α делит ребро SB в отношении 2 : 7, считая от вершины S.
б) Найдите расстояние между прямыми SA и KM.
6. Сторона правильной треугольной призмы ABCA1B1C1 равна 8. Высота этой призмы равна 6.
а) Докажите, что плоскость, содержащая прямую 
и параллельная прямой 
делит пополам ребро 
7. Дана треугольная пирамида DABC, точки M, N, P и Q лежат на рёбрах AB, BC, AD, CD, причём AM : MB = CN : NB = 3 : 1. Точки P и Q — середины рёбер DA и DC соответственно.
а) Докажите, что точки P, Q, M и N лежат в одной плоскости.
б) Найдите отношение многоугольников на которые делит плоскость PQM пирамиду.
8. ABCA 1 B 1 C 1 — правильная призма, сторона AB равна 16. Через точки M и P, лежащие на рёбрах AC и BB1 соответственно, проведена плоскость α, параллельная прямой AB. Сечение призмы этой плоскостью — четырёхугольник, одна сторона которого равна 16, а три другие равны между собой.
а) Докажите что периметр сечения призмы плоскостью α больше 40.
б) Найдите расстояние от точки A до плоскости α, если упомянутый периметр равен 46.
9. В правильной треугольной призме ABCA1B1C1 сторона основания 
а боковое ребро AA1 = 5.
а) Найдите длину отрезка A1K, где K — середина ребра BC.
10. В основании пирамиды SABCD лежит прямоугольник ABCD со стороной AB = 4 и диагональю BD = 7. Все боковые рёбра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка E, а на ребре AS — точка F так, что SF = BE = 3.
б) Плоскость CEF пересекает ребро SD в точке Q. Найдите расстояние от точки Q до плоскости ABC.
ПРОФИЛЬ ЕГЭ математика
б) Найдите угол между плоскостью α и плоскостью ADD1.
2. В правильном тетраэдре MNPQ через биссектрисы NA и QB граней MNP и QNP проведены параллельные плоскости.
а) Найдите отношение суммы объемов отсекаемых от MNPQ тетраэдров к объему MNPQ
б) Найдите расстояние между NA и QB, если ребро тетраэдра равно 1.
а) Докажите, что прямые B1P и QB перпендикулярны.
б) Найдите площадь сечения куба плоскостью, проходящей через точку P и перпендикулярной прямой BQ, если ребро куба равно 10.
4. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите площадь боковой поверхности цилиндра, если AB = 20, BB1 = 15, B1C1 = 21.
5. Дана треугольная пирамида DABC, точки M, N, P и Q лежат на рёбрах AB, BC, AD, CD, причём AM : MB = CN : NB = 3 : 1. Точки P и Q — середины рёбер DA и DC соответственно.
а) Докажите, что точки P, Q, M и N лежат в одной плоскости.
б) Найдите отношение многоугольников на которые делит плоскость PQM пирамиду.
6. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 12 и 
Длины боковых рёбер пирамиды SA = 5, SB = 13, SD = 10.
а) Докажите, что SA — высота пирамиды.
б) Найдите расстояние от вершины A до плоскости SBC.
7. а) Дан прямоугольный параллелепипед 
Докажите, что все грани тетраэдра 
— равные треугольники (тетраэдр, обладающий таким свойством, называют равногранным).
8. В правильной треугольной призме ABCA1B1C1 все рёбра равны 1.
а) Докажите, что прямая AB1 параллельна прямой, проходящей через середины отрезков AC и BC1.
б) Найдите косинус угла между прямыми AB1 и BC1.
9. Прямоугольник ABCD и цилиндр расположены таким образом, что AB — диаметр верхнего основания цилиндра, а CD лежит в плоскости нижнего основания и касается его окружности, при этом плоскость прямоугольника наклонена к плоскости основания цилиндра под углом 60°.
а) Докажите, что ABCD — квадрат.
б) Найдите длину той части отрезка BD, которая находится снаружи цилиндра, если радиус цилиндра равен 
а) Докажите, что плоскость EFT проходит через вершину D1.
б) Найдите угол между плоскостью EFT и плоскостью BB1C1.
ПРОФИЛЬ ЕГЭ математика
а) В каком отношении плоскость ETD1 делит ребро BB1?
б) Найдите угол между плоскостью ETD1 и плоскостью AA1B1.
2. В основании прямой треугольной призмы ABCA1B1C1 лежит равнобедренный треугольник ABC с основанием AC. Точка K — середина ребра A1B1, а точка M делит ребро AC в отношении AM : MC = 1 : 3.
а) Докажите, что KM перпендикулярно AC.
б) Найдите угол между прямой KM и плоскостью ABC, если AB = 12, AC = 16 и AA1 = 6.
3. В треугольной пирамиде SABC известны боковые рёбра: 
Основанием высоты этой пирамиды является середина медианы CM треугольника ABC. Эта высота равна 4.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите объём пирамиды SABC.
4. В основании правильной треугольной призмы ABCA1B1C1лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A1C1.
а) Постройте сечение призмы плоскостью BAN.
б) Найдите периметр этого сечения.
5. В основании MABCD лежит прямоугольник ABCD со сторонами AB = 4 и BC = 
все боковые ребра пирамиды равны 4. На диагонали BD основания ABCD отмечена точка Е, а на ребрах AM и AB — точка F и G соответственно так, что MF = BE = BG = 3.
а) Докажите, что плоскость GEF проходит через точку C.
б) Найдите длину отрезка, по которому плоскость GEF пересекает грань CMD пирамиды.
6. Длина ребра правильного тетраэдра ABCD равна 1. M — середина ребра BC, L — середина ребра AB.
а) Докажите, что плоскость, параллельная прямой CL и содержащая прямую DM, делит ребро AB в отношении 3 : 1, считая от вершины A.
б) Найдите угол между прямыми DM и CL.
7. Дана пирамида SABC, в которой 
а) Докажите, что ребро SA перпендикулярно ребру BC.
б) Найдите расстояние между ребрами BC и SA.
8. Радиус основания конуса равен 12, а высота конуса равна 5.
а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие.
б) Найдите расстояние от плоскости сечения до центра основания конуса.
9. В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB = 6, а боковое ребро 
На рёбрах AB, A1D1 и C1D1 отмечены точки M, N и K соответственно, причём AM = A1N = C1K = 1.
а) Пусть L — точка пересечения плоскости MNK с ребром BC. Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
10. В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точка N — середина ребра AC, точка O центр основания пирамиды, точка P делит отрезок SO в отношении 3 : 1, считая от вершины пирамиды.
а) Докажите, что прямая NP перпендикулярна прямой BS.
б) Найдите расстояние от точки B до прямой NP.
Какое наибольшее число ребер куба может пересечь одна плоскость четыре пять три шесть
Ребро куба ABCDA1B1C1D1 равно 12. Точка P — середина ребра СВ, точка K лежит на ребре CD так, что KD : KC = 1 : 2. Плоскость, проходящая через точки P, K и A1 пересекает ребро DD1 в точке M.
б) Найдите угол между плоскостями PKA1 и ABC.
Воспользуемся координатным методом исследования. Поместим заданный куб в декартову систему координат, как показано на рисунке. В таком случае имеем точки: A1(12; 0; 12), K(8; 12; 0), P(0; 6; 0).
Будем искать уравнение плоскости PKA1. Примем d = 24. Тогда:
Итак, уравнение плоскости PKA: 3x − 4y − 5z + 24 = 0.
а) Найдем аппликату точки М. Ее абсцисса и ордината имеют значения 12 и 12 соответственно.
Отсюда: DM = 2,4; D1M = 12 − 2,4 = 9,6. DM :D1M = 2,4 : 9,6 = 1 : 4, что и требовалось доказать.
б) Плоскость ABC имеет уравнение: z = 0. Если φ — искомый угол, то: