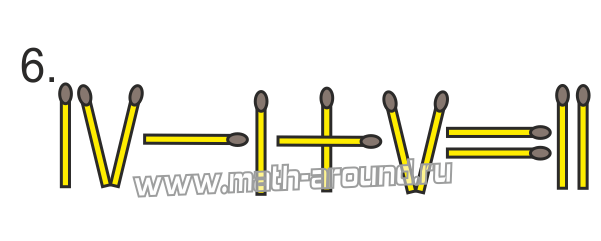
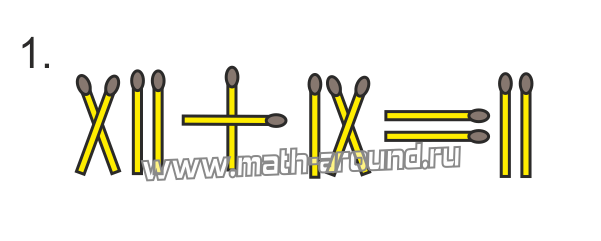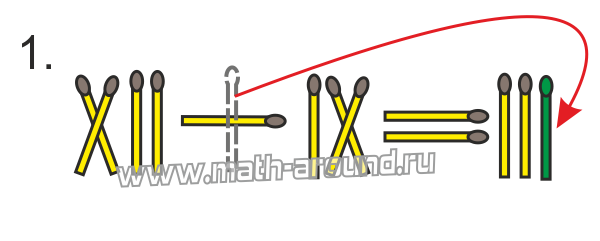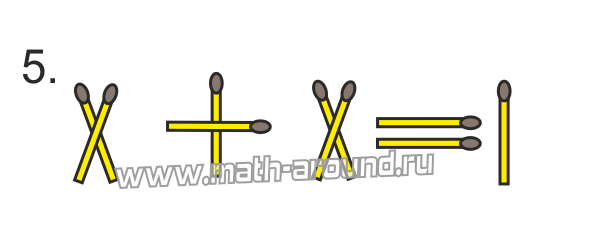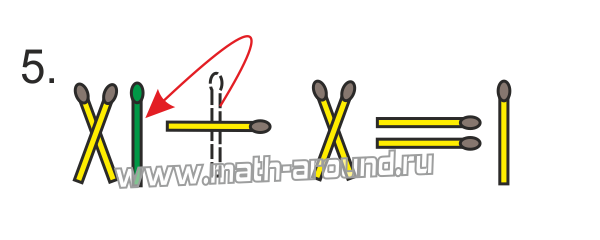какое минимальное количество палочек нужно переложить чтобы уравнение стало верным римские цифры

В выложенных из палочек равенствах с римскими цифрами допущены ошибкию Как надо переложить по одной палочке в каждом

Ответ или решение 2

Для удобства перепишем примеры, используя современные цифры:

Очевидно, что одну палочку необходимо переложить так, чтобы получилась операция сложения 5 + 6 = 11, или V + VI=XI.

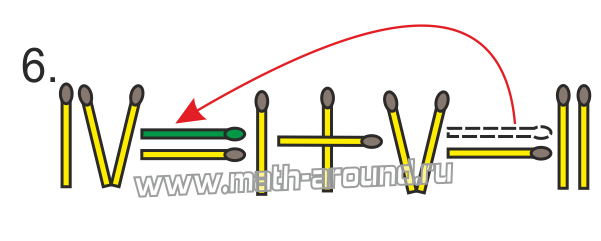
Перекладываем палочку со знака «плюс» к первому числу в конце: 11 – 10 = 1, или XI – X = I.

Аналогично второму примеру.

13 – 9 = 2, или XIII – IX = II.

Решение головоломок с палочками (со спичками) требует нестандартного мышления и пространственного воображения. Они бывают разной сложности, иногда имеют несколько решений и часто содержат какие-то подвохи, затрудняющие найти ошибку в логических рассуждениях. Основная масса заданий со спичками требует переложить одну или несколько спичек так, чтобы начало соблюдаться какое-то условие задания.

Анализ головоломок с римскими числами

Чтобы разгадывать такие головоломки необходимо знать римскую нумерацию. Из условия задачи известно, что в выложенных из палочек равенствах с римскими числами допущены ошибки: VI – VI = XI; X + X = I; XII + IX = II. Запишем эти равенства с помощью арабских чисел: 6 – 6 = 11; 10 + 10 = 1; 12 + 9 = 2.

Чтобы ответить на вопрос, как надо переложить по одной палочке в каждом равенстве, что бы исправить ошибку, необходимо:

Решение головоломок с римскими числами

В примере 6 – 6 = 11 достаточно заменить вычитание сложением, а цифру 6 на 5, и получится верное равенство: 5 + 6 = 11. Значит, палочку от цифры VI переложим на знак минус, получим: V + VI = XI.

В примере 10 + 10 = 1 достаточно заменить сложение вычитанием, а второе слагаемое 10 на 9, и получится верное равенство: 10 – 9 = 1. Значит, палочку от знака + переложим к числу Х, получим: X – IX = I.

Аналогично в примере 12 + 9 = 2 получаем: XII – IX = III.

Ответ: верные равенства V + VI = XI; X – IX = I; XII – IX = III.

Источник

Римские цифры

Это учебная статья по математике, перед началом занятий мы рекомендуем ознакомиться с вводной частью

Для этого занятия вам не потребуется ничего, кроме коробочки спичек (а лучше – счётных палочек или карандашей) и смекалки.

Первая часть занятия посвящена римским цифрам. В настоящее время зачастую дети не знакомы с ними. Поэтому прежде, чем перейти непосредственно к задачам, стоит сначала поговорить о том, как выглядят эти цифры и как их можно складывать из палочек или спичек. Цифры эти придумали этруски, ещё около 500 лет до нашей эры, но широкое применение им дали именно римляне, отчего и закрепилось за этими цифрами такое название.

Из этих примеров легко догадаться, как римскими числами записываются 50, 100, 500, 1000.

Получилось? Конечно, это латинские буквы L; С; D; M.

Для правильной записи больших чисел римскими цифрами следует сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.

Пример: число 1988. Одна тысяча – M, девять сотен – CM, восемьдесят – LXXX, восемь – VIII. Запишем их вместе: MCMLXXXVIII.

Довольно часто, чтобы выделить числа в тексте, над ними рисовали черту. Иногда черту рисовали и сверху, и снизу – в частности, так принято выделять римские цифры в русском рукописном тексте (в типографском наборе это не используют из-за технической сложности).

Безусловно, рассказывать или нет приведённую выше информацию, вы определяете сами, исходя из заинтересованности ребёнка. Для понимания дальнейшего достаточно только знания записи римскими цифрами чисел от 1 до 20. Прежде чем переходить к задачам, попрактикуйтесь вместе с ребёнком складывать числа из палочек или спичек.

Задача 1.

Как из двух спичек сложить «пять»?

Решение:

Очень просто. Нужно сложить «галочку» – римскую цифру 5.

Задача 2.

Закончите равенство римским числом:

Решение.

Ответ:

Чтобы убедиться, что ребёнок свободно обращается с римскими цифрами, вы можете придумать несколько таких равенств самостоятельно и предложить вашему ученику их выложить из палочек.

В следующем блоке задач нужно будет перекладывать или убирать указанное в условии количество «спичек» так, чтобы получались верные равенства. Разберём на примере.

Задача 3.

Переложив одну спичку, сделайте верным равенство.

Решение.

(Убираемые спички отмечены серым цветом, а их новое местоположение – розовым.)

10 + 2 = 12 – получилось верное равенство!

Заметим, что у некоторых задач на исправление равенства может быть несколько решений. Так, эта задача имеет и второе решение:

9 + 3 = 11 − мы получили ещё одно верное равенство!

Иногда встречаются задачи, где из «спичек» выложены различные забавные фигуры, в которых нужно осуществить некоторые «действия» путём перекладывания определённого количества спичек. Конечно, запрещается ломать спички или перекладывать их так, чтобы какие-то части «рисунка» были «лишними». Разберём одну такую задачу.

Задача 4.

На рисунке изображена корова. Переложите 2 спички так, чтобы корова «смотрела» в другую сторону.

Решение.

Для того, чтобы показать, что корова «смотрит» в другую сторону – достаточно повернуть корове голову.

В заключение добавим, что вы можете придумать массу подобных задач самостоятельно, и если будет желание, поделиться ими с авторами занятий!

Испытайте свои знания!

Для самых умных и талантливых учеников мы проводим на сайте дистанционную интернет-олимпиаду. Сразу же после прохождения олимпиады показываются результаты и полный разбор задач для работы над ошибками. В зависимости от успехов олимпиадника выдаются электронные дипломы и похвальные грамоты.

Каждый участник получает электронный сертификат участника.

Источник

В выложенных из палочек равенства с римскими цифрами допущены ошибки. Как надо переложить одной палочке в каждом равенстве,чтобы

Ответ или решение 2

1. V!+V=X!, то есть мы переставляем вертикальную палочку от второй V!, меняя «-» на +. Получается: 6+5=11.

2.V+V!=X!, то есть мы переставляем вертикальную палочку от первой V!, меняя «-» на +. Получается: 6+5=11.

Убираем вертикальную палочку из «+» и переставляем к первой Х, получается:

Убираем вертикальную палочку из «+» и переставляем за знак равенства, получается:

В задаче приведено несколько примеров с использованием римских цифр. Эти примеры выложены на столе с помощью спичек. В каждом из них необходимо поменять месторасположение одной из спичек так, чтобы получилось верное равенство.

Римские цифры

Для записи чисел из первых нескольких десятков, в частности, от 1 до 20, используются комбинации следующих римских цифр:

По правилам расчета чисел, римское число XI соответствует 11:

а римское IV соответствует числу 4:

Получение верных равенств

Очевидно, что знак «-» надо поменять на «+», чтобы увеличить значение в правой части. Это можно сделать, если переставить римскую цифру I. Есть три варианта, из которых нас устраивает два:

VI + V = XI или 6 + 5 = 11;

V + VI = XI или 5 + 6 = 11;

Во втором примере дано:

В этом примере надо уменьшить левую часть, поменяв знак «+» на «-». Переложить вертикальную спичку в знаке «+», можно несколькими способами, из которых нас устраивает только один:

также надо уменьшить левую часть, поменяв знак «+» на «-». Есть несколько способов, как это сделать, из которых подходит только один:

Источник

Скоро вебинар
«ПРЯМАЯ НА ПЛОСКОСТИ»
(Аналитическая геометрия). Жми подробнее.

Арифметика и спички (римские числа)

При решении задач со спичками в этом разделе Вам необходимо знать написание и значение римских чисел, а также уметь считать в пределах 20.

Перейти на арифметические задачи с арабскими цифрами.

Задача1.Из спичек сложили неверные равенства:
Переложите в каждом равенстве по одной спичке так, чтобы равенства стали верным. Возможно несколько правильных ответов.

Автор: Аникина Марина

Комментарии к этой заметке:

Наталья, доброго времени суток! В задании указано, что переложить можно только одну спичку. Давайте посмотрим на ваш ответ и посчитаем сколько раз мы передвинем спичку (см. рисунок ниже).

Спичку передвинули 3 раза.Т.о., решение VI-I+V=X для данной задачи неверно.

Добавить Ваш комментарий

Хотите внести свою лепту в его развитие!? Тогда Вам сюда!

Источник

Со спичками не шутят

Несмотря на огромные перемены в образе жизни, произошедшие в последние годы, из нее не пропали спички. Смартфоны вытесняют фотоаппараты, видеокамеры, калькуляторы и компьютеры, а зажигалки не смогли вытеснить окончательно простые спички. Поэтому сохраняются головоломки, игры, фокусы со спичками. Эта книга – гимн спичкам в прозе. Собрание занимательных, познавательных, развивающих материалов, распределенных как в школе, по отдельным учебным предметам. Добро пожаловать в школу самообразования. Надеюсь, это не будет очень скучно.

Оглавление

Приведённый ознакомительный фрагмент книги Со спичками не шутят предоставлен нашим книжным партнёром — компанией ЛитРес.

Урок 1. Цифры, буквы и немного математики

— Сколько будет, если восемь разделить пополам?

— Если вдоль, то три, а если поперек, то ноль.

При решении задач первого урока спичками нужно будет изображать цифры и буквы. Если вы улыбнулись, прочитав эпиграф, значит с арифметикой у вас всё в порядке. Тогда дерзайте. Минимальные «системные» требования к человеку, решающему задачи этой главы — знать русский и латинский алфавиты, арабское и римское написание чисел, уметь немножечко считать. В обыденной жизни римские цифры последнее время встречаются редко, но многие спичечные задачи с числами и арифметическими примерами имеют давнюю историю и поэтому в них фигурируют цифры этой, постепенно забываемой, системы счисления. Римская нумерация, в отличие от арабской системы, не позиционная. В её основе использованы принцип сложения (например, V+I=VI, то есть 5+1=6) и принцип вычитания (например, X-I=IX, 10-1=9). Основные знаки римской нумерации, в спичечном изображении, выглядят так:

Остальные числа получаются из основных следующим образом: 1=I, 2=II, 3=III, 4=IV (вычитаемое слева от основного знака), 5=V, 6=VI (прибавляют справа до трех знаков), 7=VII, 8=VIII, 9=IX (снова вычитание, вычитается слева только один знак), 10=X, 11=XI, 12=XII, 13=XIII, 14=XIV, 15=XV, 16=XVI, 17=XVII, 18=XVIII, 19=XIX, 20=XX. Далее все идет аналогично.

При изображении спичками букв и цифр возможны варианты, подбирайте подходящий для конкретной задачи. Вот как, к примеру, можно представить число «два»:

Показано четыре варианта, но можно по-другому выложить буквы в слове «два», написать это слово на другом языке, поставить сверху и снизу черточки в римской нумерации, записать это число как квадратный корень из четырех и т. д.

Предваряющие слова свели на нет интригу следующих задач, и вы можете удивиться: в чём же закавыка, всё ведь просто. Обычно подобные головоломки публикуют, не намекая столь прозрачно, что нужно сделать, но ради идеи систематизации заданий пришлось пойти на это. Если же вы захотите проверить мыслительные способности кого-то из ваших приятелей, не говорите им вступительных слов, а сразу — условие задачи и всё.

1-1. Из двух спичек, не ломая их, сделайте пять. Справившись с этим заданием, вы легко сделаете из двух спичек десять и даже пятьдесят.

1-2. Теперь возьмите три спички. Не прибавляя и не ломая их, сделайте из трех спичек четыре. А сможете сделать ещё больше?

1-3. Имея 4 спички, вы без труда сделаете 7, затем 15, наконец, 1000. А можете наоборот уменьшить число и сделать из 4 спичек 3?

1-4. На рисунке из 4 спичек сложено число 14. Переложите только одну спичку так, чтобы получилась тысяча.

1-5. Из 4 спичек сложено число 7.

а). Как переложить одну спичку, чтобы получилось число 1?

б). Как нужно переложить две спички, чтобы получилось число 5?

1-6. Разделите 5 спичек между пятью лицами так, чтобы каждый получил по спичке, и одна спичка осталась в коробке.

1-7. Из 5 спичек сделайте 6. (Есть несколько решений.)

1-8. Из 5 спичек сделайте 8.

1-9. Как доказать на спичках, что если от 8 отнять 5, то ничего не останется?

1-10. Положите 6 спичек так, чтобы получилось «ничто».

1-11. Положите 6 спичек так, как показано на рисунке.

а). Передвиньте одну из них, не касаясь других, так, чтобы получилась арифметическая дробь, равная 1. Спичку, изображающую дробную черту, трогать нельзя.

б). Превратите эту дробь в число 1/3, не изменяя количества данных спичек.

1-12. На рисунке из спичек образовано число 57 в римской нумерации. Переместив две из них, не сдвигая остальных, получите 0. Есть два различных решения.

1-13. Отнимите от 7 спичек 5 спичек так, чтобы и осталось тоже 5.

1-14. Чему равно значение дроби, показанной на рисунке семью спичками?

1-15. Переложите 1 спичку на следующем рисунке так, чтобы равенство стало верным. Существует несколько решений.

1-16. А теперь подумайте над рисунком предыдущей задачи и, не перекладывая спичек, докажите, что равенство изначально было верным.

1-17. Докажите на спичках, что половина числа 12 равна 7.

1-18. Как из 8 спичек сделать три?

1-19. Из спичек сложено математическое выражение. И, конечно же, оно не верно. А вот как его исправить, чтобы выражение стало истинным, переложив всего 1 спичку?

1-20. а). Положите 9 спичек так, чтобы получилось 10.

б). Сделайте из 9 спичек 36.

1-21. Приложите к 4 спичкам 5 спичек так, чтобы получилось 100. (Два решения.)

1-22. Докажите на спичках, что:

а) 9 без 3 равно четырем;

б) 11 без 3 равно шести;

в) половина числа 9 равна 4.

1-23. Переложите спички, показанные на рисунке, так, чтобы в каждом горизонтальном ряду было четыре (а можно сделать в каждом ряду — шесть).

1-24. Положите пять спичек. Прибавьте к ним ещё 5 спичек так, чтобы получилось три.

1-25. Из 10 спичек получите ноль.

1-26. Увеличьте число, составленное из 10 спичек, в полтора раза, переложив как можно меньше спичек.

1-27. Сможете ли вы показать с помощью спичек, как от 5 следует отнять 7/10, чтобы остаток оказался в точности равен 4?

1-28. На рисунке сложено арифметическое выражение из спичек. Какое минимальное количество спичек нужно переложить, чтобы равенство стало верным?

1-29. Переставьте одну спичку, чтобы пример имел решение.

1-30. Из 12 спичек сделайте 2.

1-31. Переложите 2 спички так, чтобы равенство стало верным.

1-32. Превратите это арифметическое выражение в истинное равенство или неравенство, взяв или переложив 1 спичку. Есть много решений.

1-33. Как из 13 целых спичек, каждая из которых равна 5 сантиметрам, положенных одна около другой, составить метр?

1-34. Переложите 2 спички так, чтобы равенство стало верным.

1-35. Из 14 спичек сделайте 50.

1-36. Положите 15 спичек так, чтобы получилась сетка.

1-37. Спички расположены как на рисунке. Убирая каждый раз несколько из них, образуйте как можно больше различных слов. Например, НОС.

1-38. Во всех следующих арифметических выражениях нужно добиться истинности равенств, переложив всего по одной спичке.

1-39. Переложите 1 спичку так, чтобы равенство выполнялось с точностью до 0,002.

1-40. Чему равен Х в изображенном спичками двойном равенстве? (Наборы из трёх вертикальных спичек можно интерпретировать тремя различными способами.)

1-41. От данных 24 спичек, расположенных указанным образом, отнять 8 спичек так, чтобы осталось 6.

1-42. Перед вами 24 спички. Можете ли вы, сняв со стола 13 спичек, сложить из оставшихся сто «Г»?

1-43. С такой же начальной конфигурацией, как и в предыдущей задаче, требуется взять 19 спичек так, чтобы осталось 8.

1-44. Из той же начальной конфигурации взять 13 спичек так, чтобы осталось 8.

1-45. От разложенных на столе 30 спичек постарайтесь отнять 13 спичек и получить три.

1-46. В каждом из трёх горизонтальных рядов переложите по одной спичке так, чтобы все шесть равенств (вертикальных и горизонтальных) оказались верными. (Задания на деление и на умножение).

1-47. У каждой из цифр 1 спичка стоит не на своем месте. Переложите по одной спичке в каждой цифре так, чтобы равенство стало верным.

1-48. В двух дробях можно убрать по 10 спичек (не трогая дробную черту) так, что величина дроби не изменится.

1-49. В этой дроби можно убрать 10 спичек и дробь не изменит значения, но затем можно убрать ещё 4 спички и величина дроби будет прежней.

1-50. Угадайте закономерность форм фигурок, сложенных из спичек. Какую фигуру следует поставить следующей?

1-51. В задаче 1-47 требовалось переложить по одной спичке в каждой цифре, теперь же предлагается в каждом равенстве переложить всего одну спичку, чтобы оно стало верным.

Подобных задач можно придумать сколько угодно. Методика их составления очень проста: выкладываете спичками верное равенство, а потом перекладываете одну из них, как-нибудь похитрее. Задача готова.

1-52. Девятнадцатью спичками выложено неверное числовое выражение. Требуется переложить всего 3 спички так, чтобы получилось правильное равенство.

1-53. В выложенной спичками записи числа 8111 переложите 3 спички таким образом, чтобы получилась запись числа 950.

1-54. В выложенной спичками записи числа 2163 переложите 3 спички таким образом, чтобы получилась запись числа 1995.

1-55. Уберите 1 спичку, чтобы равенство стало верным.

1-56. Уберите 2 спички, чтобы равенство стало верным.

1-57. Уберите 3 спички, чтобы равенство стало верным.

Источник