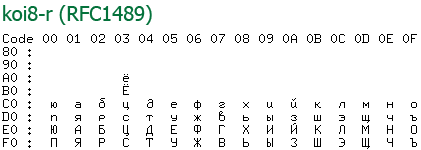какое максимальное количество комбинаций можно закодировать 1 байтом
Один байт равен 2 в степени 8. Итого 256. Как считать комбинации битов?
Если записать число 258 в виде /00000001 00000010/ вам станет понятнее?
258 не умещается в 1 байт(8 бит), поэтому для записи этого числа используется уже 2 байта. Калькулятор с помощью которого вы переводите числа в двоичную систему удалил идущие впереди нули для сокращения записи, поэтому битов вышло 9(в памяти на самом деле все равно выделилось 16). По аналогии в десятичной системе число 0000258 можно записать как 258.
По поводу количества комбинаций 0/1 в 8-ми значном числе их действительно 256.
могу лишь дополнить ответ vreitech
он может быть равен 0(00000000), или он может быть равен 1(00000001), или он может быть равен 2(00000010), или он может быть равен 3(00000011), или он может быть равен 4(00000100), или он может быть равен 5(00000101), или он может быть равен 6(00000110), или он может быть равен 7(00000111), или он может быть равен 8(00001000), или он может быть равен 9(00001001), или он может быть равен 10(00001010), или он может быть равен 11(00001011), или он может быть равен 12(00001100), или он может быть равен 13(00001101), или он может быть равен 14(00001110), или он может быть равен 15(00001111), или он может быть равен 16(00010000), или он может быть равен 17(00010001), или он может быть равен 18(00010010), или он может быть равен 19(00010011), или он может быть равен 20(00010100), или он может быть равен 21(00010101), или он может быть равен 22(00010110), или он может быть равен 23(00010111), или он может быть равен 24(00011000), или он может быть равен 25(00011001), или он может быть равен 26(00011010), или он может быть равен 27(00011011), или он может быть равен 28(00011100), или он может быть равен 29(00011101), или он может быть равен 30(00011110), или он может быть равен 31(00011111), или он может быть равен 32(00100000), или он может быть равен 33(00100001), или он может быть равен 34(00100010), или он может быть равен 35(00100011), или он может быть равен 36(00100100), или он может быть равен 37(00100101), или он может быть равен 38(00100110), или он может быть равен 39(00100111), или он может быть равен 40(00101000), или он может быть равен 41(00101001), или он может быть равен 42(00101010), или он может быть равен 43(00101011), или он может быть равен 44(00101100), или он может быть равен 45(00101101), или он может быть равен 46(00101110), или он может быть равен 47(00101111), или он может быть равен 48(00110000), или он может быть равен 49(00110001), или он может быть равен 50(00110010), или он может быть равен 51(00110011), или он может быть равен 52(00110100), или он может быть равен 53(00110101), или он может быть равен 54(00110110), или он может быть равен 55(00110111), или он может быть равен 56(00111000), или он может быть равен 57(00111001), или он может быть равен 58(00111010), или он может быть равен 59(00111011), или он может быть равен 60(00111100), или он может быть равен 61(00111101), или он может быть равен 62(00111110), или он может быть равен 63(00111111), или он может быть равен 64(01000000), или он может быть равен 65(01000001), или он может быть равен 66(01000010), или он может быть равен 67(01000011), или он может быть равен 68(01000100), или он может быть равен 69(01000101), или он может быть равен 70(01000110), или он может быть равен 71(01000111), или он может быть равен 72(01001000), или он может быть равен 73(01001001), или он может быть равен 74(01001010), или он может быть равен 75(01001011), или он может быть равен 76(01001100), или он может быть равен 77(01001101), или он может быть равен 78(01001110), или он может быть равен 79(01001111), или он может быть равен 80(01010000), или он может быть равен 81(01010001), или он может быть равен 82(01010010), или он может быть равен 83(01010011), или он может быть равен 84(01010100), или он может быть равен 85(01010101), или он может быть равен 86(01010110), или он может быть равен 87(01010111), или он может быть равен 88(01011000), или он может быть равен 89(01011001), или он может быть равен 90(01011010), или он может быть равен 91(01011011), или он может быть равен 92(01011100), или он может быть равен 93(01011101), или он может быть равен 94(01011110), или он может быть равен 95(01011111), или он может быть равен 96(01100000), или он может быть равен 97(01100001), или он может быть равен 98(01100010), или он может быть равен 99(01100011), или он может быть равен 100(01100100), или он может быть равен 101(01100101), или он может быть равен 102(01100110), или он может быть равен 103(01100111), или он может быть равен 104(01101000), или он может быть равен 105(01101001), или он может быть равен 106(01101010), или он может быть равен 107(01101011), или он может быть равен 108(01101100), или он может быть равен 109(01101101), или он может быть равен 110(01101110), или он может быть равен 111(01101111), или он может быть равен 112(01110000), или он может быть равен 113(01110001), или он может быть равен 114(01110010), или он может быть равен 115(01110011), или он может быть равен 116(01110100), или он может быть равен 117(01110101), или он может быть равен 118(01110110), или он может быть равен 119(01110111), или он может быть равен 120(01111000), или он может быть равен 121(01111001), или он может быть равен 122(01111010), или он может быть равен 123(01111011), или он может быть равен 124(01111100), или он может быть равен 125(01111101), или он может быть равен 126(01111110), или он может быть равен 127(01111111), или он может быть равен 128(10000000), или он может быть равен 129(10000001), или он может быть равен 130(10000010), или он может быть равен 131(10000011), или он может быть равен 132(10000100), или он может быть равен 133(10000101), или он может быть равен 134(10000110), или он может быть равен 135(10000111), или он может быть равен 136(10001000), или он может быть равен 137(10001001), или он может быть равен 138(10001010), или он может быть равен 139(10001011), или он может быть равен 140(10001100), или он может быть равен 141(10001101), или он может быть равен 142(10001110), или он может быть равен 143(10001111), или он может быть равен 144(10010000), или он может быть равен 145(10010001), или он может быть равен 146(10010010), или он может быть равен 147(10010011), или он может быть равен 148(10010100), или он может быть равен 149(10010101), или он может быть равен 150(10010110), или он может быть равен 151(10010111), или он может быть равен 152(10011000), или он может быть равен 153(10011001), или он может быть равен 154(10011010), или он может быть равен 155(10011011), или он может быть равен 156(10011100), или он может быть равен 157(10011101), или он может быть равен 158(10011110), или он может быть равен 159(10011111), или он может быть равен 160(10100000), или он может быть равен 161(10100001), или он может быть равен 162(10100010), или он может быть равен 163(10100011), или он может быть равен 164(10100100), или он может быть равен 165(10100101), или он может быть равен 166(10100110), или он может быть равен 167(10100111), или он может быть равен 168(10101000), или он может быть равен 169(10101001), или он может быть равен 170(10101010), или он может быть равен 171(10101011), или он может быть равен 172(10101100), или он может быть равен 173(10101101), или он может быть равен 174(10101110), или он может быть равен 175(10101111), или он может быть равен 176(10110000), или он может быть равен 177(10110001), или он может быть равен 178(10110010), или он может быть равен 179(10110011), или он может быть равен 180(10110100), или он может быть равен 181(10110101), или он может быть равен 182(10110110), или он может быть равен 183(10110111), или он может быть равен 184(10111000), или он может быть равен 185(10111001), или он может быть равен 186(10111010), или он может быть равен 187(10111011), или он может быть равен 188(10111100), или он может быть равен 189(10111101), или он может быть равен 190(10111110), или он может быть равен 191(10111111), или он может быть равен 192(11000000), или он может быть равен 193(11000001), или он может быть равен 194(11000010), или он может быть равен 195(11000011), или он может быть равен 196(11000100), или он может быть равен 197(11000101), или он может быть равен 198(11000110), или он может быть равен 199(11000111), или он может быть равен 200(11001000), или он может быть равен 201(11001001), или он может быть равен 202(11001010), или он может быть равен 203(11001011), или он может быть равен 204(11001100), или он может быть равен 205(11001101), или он может быть равен 206(11001110), или он может быть равен 207(11001111), или он может быть равен 208(11010000), или он может быть равен 209(11010001), или он может быть равен 210(11010010), или он может быть равен 211(11010011), или он может быть равен 212(11010100), или он может быть равен 213(11010101), или он может быть равен 214(11010110), или он может быть равен 215(11010111), или он может быть равен 216(11011000), или он может быть равен 217(11011001), или он может быть равен 218(11011010), или он может быть равен 219(11011011), или он может быть равен 220(11011100), или он может быть равен 221(11011101), или он может быть равен 222(11011110), или он может быть равен 223(11011111), или он может быть равен 224(11100000), или он может быть равен 225(11100001), или он может быть равен 226(11100010), или он может быть равен 227(11100011), или он может быть равен 228(11100100), или он может быть равен 229(11100101), или он может быть равен 230(11100110), или он может быть равен 231(11100111), или он может быть равен 232(11101000), или он может быть равен 233(11101001), или он может быть равен 234(11101010), или он может быть равен 235(11101011), или он может быть равен 236(11101100), или он может быть равен 237(11101101), или он может быть равен 238(11101110), или он может быть равен 239(11101111), или он может быть равен 240(11110000), или он может быть равен 241(11110001), или он может быть равен 242(11110010), или он может быть равен 243(11110011), или он может быть равен 244(11110100), или он может быть равен 245(11110101), или он может быть равен 246(11110110), или он может быть равен 247(11110111), или он может быть равен 248(11111000), или он может быть равен 249(11111001), или он может быть равен 250(11111010), или он может быть равен 251(11111011), или он может быть равен 252(11111100), или он может быть равен 253(11111101), или он может быть равен 254(11111110), или он может быть равен 255(11111111)
Кодирование для чайников, ч.1
Не являясь специалистом в обозначенной области я, тем не менее, прочитал много специализированной литературы для знакомства с предметом и прорываясь через тернии к звёздам набил, на начальных этапах, немало шишек. При всём изобилии информации мне не удалось найти простые статьи о кодировании как таковом, вне рамок специальной литературы (так сказать без формул и с картинками).
Статья, в первой части, является ликбезом по кодированию как таковому с примерами манипуляций с битовыми кодами, а во второй я бы хотел затронуть простейшие способы кодирования изображений.
0. Начало
Давайте рассмотрим некоторые более подробно.
1.1 Речь, мимика, жесты
1.2 Чередующиеся сигналы
В примитивном виде кодирование чередующимися сигналами используется человечеством очень давно. В предыдущем разделе мы сказали про дым и огонь. Если между наблюдателем и источником огня ставить и убирать препятствие, то наблюдателю будет казаться, что он видит чередующиеся сигналы «включено/выключено». Меняя частоту таких включений мы можем выработать последовательность кодов, которая будет однозначно трактоваться принимающей стороной.
1.3 Контекст
2. Кодирование текста
Текст в компьютере является частью 256 символов, для каждого отводится один байт и в качестве кода могут быть использованы значения от 0 до 255. Так как данные в ПК представлены в двоичной системе счисления, то один байт (в значении ноль) равен записи 00000000, а 255 как 11111111. Чтение такого представления числа происходит справа налево, то есть один будет записано как 00000001.
Итак, символов английского алфавита 26 для верхнего и 26 для нижнего регистра, 10 цифр. Так же есть знаки препинания и другие символы, но для экспериментов мы будем использовать только прописные буквы (верхний регистр) и пробел.
Тестовая фраза «ЕХАЛ ГРЕКА ЧЕРЕЗ РЕКУ ВИДИТ ГРЕКА В РЕЧКЕ РАК СУНУЛ ГРЕКА РУКУ В РЕКУ РАК ЗА РУКУ ГРЕКУ ЦАП».
2.1 Блочное кодирование
Информация в ПК уже представлена в виде блоков по 8 бит, но мы, зная контекст, попробуем представить её в виде блоков меньшего размера. Для этого нам нужно собрать информацию о представленных символах и, на будущее, сразу подсчитаем частоту использования каждого символа:
Биты, байты, кодировки
Почти полтора месяца писала данную статью, но надеюсь оно того стоило. Данная статья может выглядеть холиварной, поэтому не спешите писать комментарии пока не прочитаете полностью. Статья главным образом о методологии.
Дело в том, что я твёрдо уверена, что в учебных заведениях по информационной специальности, школьникам и студентам забивают голову историей древнего мира вместо актуальных знаний. Все методички преподают дамы бальзаковского возраста, а пишут эти методички профессора возраста Карла Маркса. В результате от соискателей на работу, и от стажёров, я слышала такие забавные заблуждения, относительно фундаментальных основ, как:
В числе прочих забавных случаев: для выбора десяти случайных чисел из бд, соискатели десять раз делают запрос; для открытия файла на чтение используют в PHP флаг ‘a+’; не умеют работать со строками, кодировками и указателями. Написать функцию, которая возвращает строку задом наперёд, не используя переменную-буфер — вообще непосильная задача.
В этой статье, я хочу коснуться проблемы заблуждений с битами и байтами, и написать свою методику обучения этим фундаментальным знаниям.
Итак… сперва я хочу написать определения из википедии методичек, которые являются догмой в умах профессоров из мин.образования.
Из-за этих определений, в умах будущих программистов ЭВМ, больше каши, чем из-за каких-либо других определений! Они совершенно истинны, но совершенно бесполезны для обучения. Я превращаюсь в Халка, когда слышу их.
Про биты
Итак, дети, садитесь, урок первый, представьте себе выключатель. Нет, не двоичный логарифм вероятности… А обычный такой выключатель, тумблер, рычажок, что угодно, включающее например лампочку, когда находится в одном положении и выключающее в другом. На некоторых рычажках даже подписывают буковки I/O, как указатели положений ручки. Нет, выключатель не несёт в себе информацию. Он выключает свет.
У выключателя есть два положения — вкл/выкл. Если мы поставим рядом два выключателя, то количество комбинаций позиций, которое могут занимать их ручки — четыре. (Когда оба выключены, когда оба включены, и две комбинации когда включен только один из них). Если мы возьмём систему из трёх выключателей — они смогут занимать восемь комбинаций. И так далее, N выключателей имеют 2^N комбинаций. Выключатель который имеет только два положения (вкл/выкл) мы можем назвать битом. Если мы представим, что положениям вкл/выкл соответствуют числа 1 и 0, то можно легко записать какое-нибудь целое число в двоичной системе счисления, используя только последовательный набор выключателей, так чтобы каждый выключатель отвечал за свой двоичный разряд.
Безусловно выключатели мы можем применить к магнитной дорожке, или оптическому диску, так, чтобы при помощи специального устройства можно было «включать» или «выключать» их маленькие участки. Теперь мы наконец подошли к тому, что все компьютерные запоминающие устройства состоят из «ноликов и единичек».
Однако, в этих ноликах и единичках нам надо хранить информацию. Какую же информацию нам можно хранить? Давайте рассмотрим один бит. Мы можем условно договориться, что он может хранить информацию, и два его состояния вкл/выкл содержат значения «баклажан» и «не баклажан» соответственно. Это отлично подходит, когда нам надо произвести учёт баклажанов! Однако в реальном мире компьютеры, которые умеют только считать баклажаны — не пользуются спросом. Выходит выключатель (бит) не может нести в себе информацию. Чтобы записывать ноликами и единичками какую-то информацию, было решено группировать их по несколько штук, и такую группу называть байтом.
На заре компьютеров байты составляли 4, потом 5, потом 6 бит… Группа из 6 бит может принимать целых 64 значений. Вполне неплохо, так как можно создать некую таблицу соответствий этих значений определённым символам — кодировку. Такая кодировка уже может содержать цифры и заглавные буквы латинского алфавита, а также некоторые арифметические знаки. «Шестибитные-кодировки» — применялись на компьютерах в 1950-х — 1960-х годах.
Для человека который только начинает изучать информатику, будет понятно и легко запомнить что байт — является минимальной единицей информации. В байт можно записать какое-нибудь число, либо например какой-нибудь символ из таблицы символов (англ. charset, буквально «набор символов») — кодировки (codepage, encoding).
С развитием компьютеров, появилась потребность в большем количестве значений для байта. В 1963-м году появилась первая редакция семибитной кодировки ASCII. Поэтому байты стали занимать 7 бит. 7 бит, требующиеся для одного символа данной кодировки позволяют использовать 128 значений. В этой кодировке уже были включены строчные латинские символы, и больший набор управляющих и арифметических символов.
Всемирное распространение компьютеров подтолкнуло дальнейшее расширение границ занимаемых байтом. Для различных языков требовалось чтобы таблица символов также могла хранить алфавит того языка, где используется данная ЭВМ. На текущий момент восемь — это последнее и видимо окончательное количество бит составляющих байт. Соответственно байт может принимать 256 значений. По сравнению с таблицей ASCII в. новых таблицах символов — организовалось 128 вакантных мест. Теперь я думаю можно рассказать как значения хранятся в различных кириллических кодировках.
Кодировки
Итак, чтобы хранить символы не входящие в ASCII, необходимо было придумать новые кодировки. Поскольку до этого таблица ASCII была наиболее подходящей (были и другие), то она и пошла в основу новых кодировок. Поэтому следующие кодировки отличаются только значениями начиная с 80 (hex). Для наглядности оставлю только кириллические символы.
Так выглядела наиболее популярная кодировка под DOS. Примечательно что файлы в этой кодировке до сих пор встречаются. Как правило среди устаревшей архивной информации, в программах WinRar, Блокнот и WordPad, до сих пор есть опции «открыть как текст DOS», впрочем последними двумя мало кто пользуется =).
Кодировка koi8 была примечательна тем, что русские буквы там располагались на позициях английских звуков из нижней половины (т. е. ASCII). Это когда-то давно позволяло смягчить переход со старых серверов понимающие только ascii на новые, что было актуально среди почтовых серверов. Смысл был в том что если отправленное вами письмо приходило на старый сервер, то пользователю оно показывалось как транслит, что позволяло хоть как-то понять текст письма.
Самая популярная у нас в России однобайтная кодировка, на сегодняшний день, это именно «windows-1251». Разумеется популярность её целиком обусловлена популярностью Windows среди других операционных систем. Возможностей кодировки вполне хватает для использования её в широком круге задач. Например движок моего блога, по-умолчанию, использует для работы именно данную кодировку.
Я не могу не упомянуть о кодировке ISO, Удивительно, но несмотря на то что её никто никогда не использовал, эта кодировка является единственной кодировкой имеющей статус стандарта.
На примере данных кодировок видно, как один байт может хранить какое угодно символьное значение русского и английского языков, а также цифр и знаков пунктуации.
Но что делать когда этого не достаточно?
Многобайтные кодировки
Если вам хочется создать кодировку которая бы имела коды одновременно для русского и греческого алфавита? Одним байтом тут не отделаться. Появилась задача разработать кодировку один знак которой может занимать больше чем один байт, так как два байта могут принимать уже 2^16 = 65536 значений, а четыре байта аж 4294967296. Поэтому сначала придумали стандарт кодирования символов — Юникод, который включал бы в себя максимально полный перечень символов которые может принимать один знак.
Первая версия Юникода (Unicode 1991 г.) представляла собой 16-битную кодировку с фиксированной шириной символа; общее число разных символов было 2 16 (65 536).
Вторая версия Юникода (UCS-2), стала называться UTF-16, она позволяла гораздо расширить количество возможных значений, также используя для символов 16-битные последовательности (т. е. по 2 или по 4 байта на символ).
Символы с кодами 0×0000.0xD7FF и 0xE000.0xFFFF представляются одним 16-битным словом, а символы с кодами 0×10000–0×10FFFF — в виде последовательности двух 16-битных слов. Количество символов, представляемых двумя 16-битными словами равно (2 20 ). Для представления символов с кодами 0×10000–0×10FFFF используется матрица перекодировки. Первое слово из двух переданных лежит в диапазоне 0xD800-0xDBFF, а второе — 0xDC00-0xDFFF. Именно этот диапазон значений не может встречаться среди символов, передаваемых с помощью одного 16-битного слова, так что расшифровка кодировки всегда однозначна. Ясно, что имеется как раз 2 10 * 2 10 = 2 20 таких комбинаций.
Кодировка UTF-32 (UCS-4) использует по 32 бита, или 4 байта на хранение одного символа. Строго говоря, стандарт Unicode не описывает символы со значениями выше 2^21, так что хватило бы и трёх байт, на символ, вероятно компьютеры работают несколько быстрее с мелкими блоками памяти кратными двум, или для того чтобы в сектор диска попадало кратное количество символов. Так или иначе это единственная из многобайтных кодировок с постоянной длиной. Помимо недостатка — использования четырёх байт на символ, у неё есть и очевидное преимущество — возможность прямой адресации к N-ному символу. В других кодировках требуется последовательное вычисление позиции каждого символа. Поэтому текстовые редакторы, внутри себя хранят всю информацию в виде UCS-4.
В 1992 году Кеном Томпсоном и Робом Пайком был изобретён формат UTF-8. Он отличается тем, что он ASCII совместим, и значения из таблицы Юникода могут занимать от 1 до 4х символов.
Символы UTF-8 получаются из Unicode следующим образом:
| Unicode | UTF-8 | Представленные символы |
|---|---|---|
| 0×00000000 — 0×0000007F | 0xxxxxxx | ASCII, в том числе английский алфавит, простейшие знаки препинания и арабские цифры |
| 0×00000080 — 0×000007FF | 110xxxxx 10xxxxxx | кириллица, расширенная латиница, арабский, армянский, греческий, еврейский и коптский алфавит; сирийское письмо, тана, нко; МФА; некоторые знаки препинания |
| 0×00000800 — 0×0000FFFF | 1110xxxx 10xxxxxx 10xxxxxx | все другие современные формы письменности, в том числе грузинский алфавит, индийское, китайское, корейское и японское письмо; сложные знаки препинания; математические и другие специальные символы |
| 0×00010000 — 0×001FFFFF | 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx | музыкальные символы, редкие китайские иероглифы, вымершие формы письменности |
Заключение
Вот собственно и всё что я хотела рассказать. Я считаю что очень интересно разбираться в том как работает компьютер, знать как хранятся в нём символы которые я набираю на клавиатуре, представлять насколько однобайтная кодировка например win-1251 (или utf-32 с фикс. длиной) работает быстрее со строковыми функциями и почему и т. п. Надеюсь статья вам понравилась.
Большое спасибо Википедии за возможность скопировать цитаты и таблицы, а то бы писала статью ещё месяц.
Все кто хочет узнать больше, также могут почитать про то в каком порядке записываются байты в кодировках UTF-16 и UTF-32 — в википедии тут и тут. А также что такое порядок байтов тут: Порядок_байтов. Также интересна будет статья Юникод в операционных системах Microsoft.