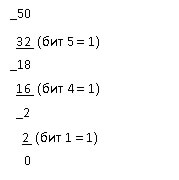какое количество бит содержит слово корова
Какое количество бит содержит слово корова
Для информации существуют свои единицы измерения информации. Если рассматривать сообщения информации как последовательность знаков, то их можно представлять битами, а измерять в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах и петабайтах.
Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.
Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.
Байт – основная единица измерения количества информации.
Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.
Производные единицы измерения количества информации
1 килобайт (Кб)=1024 байта =2 10 байтов
1 мегабайт (Мб)=1024 килобайта =2 10 килобайтов=2 20 байтов
1 гигабайт (Гб)=1024 мегабайта =2 10 мегабайтов=2 30 байтов
1 терабайт (Гб)=1024 гигабайта =2 10 гигабайтов=2 40 байтов
Методы измерения количества информации
Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:
Алфавитный подход к измерению количества информации
При этом подходе отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка, т.е. его алфавит можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет в себе каждый символ:
Вероятностный подход к измерению количества информации
Этот подход применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:
I – количество информации,
N – количество возможных событий,
Pi – вероятность i-го события.
Задача 1.
Шар находится в одной из четырех коробок. Сколько бит информации несет сообщение о том, в какой именно коробке находится шар.
Имеется 4 равновероятных события (N=4).
По формуле Хартли имеем: 4=2 i . Так как 2 2 =2 i , то i=2. Значит, это сообщение содержит 2 бита информации.
Задача 2.
Чему равен информационный объем одного символа русского языка?
В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа. I=log2 N=log2 32=5 битов (2 5 =32).
Примечание. Если невозможно найти целую степень числа, то округление производится в большую сторону.
Задача 3.
Чему равен информационный объем одного символа английского языка?
Задача 4.
Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний (“включено” или “выключено”). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 N сигналов.
2 5 6 , поэтому пяти лампочек недостаточно, а шести хватит. Значит, нужно 6 лампочек.
Задача 5.
Метеостанция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
В данном случае алфавитом является множество чисел от 0 до 100, всего 101 значение. Поэтому информационный объем результатов одного измерения I=log2101. Но это значение не будет целочисленным, поэтому заменим число 101 ближайшей к нему степенью двойки, большей, чем 101. это число 128=2 7 . Принимаем для одного измерения I=log2128=7 битов. Для 80 измерений общий информационный объем равен 80*7 = 560 битов = 70 байтов.
Задача 6.
Определите количество информации, которое будет получено после подбрасывания несимметричной 4-гранной пирамидки, если делают один бросок.
Пусть при бросании 4-гранной несимметричной пирамидки вероятности отдельных событий будут равны: p1=1/2, p2=1/4, p3=1/8, p4=1/8.
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
Задача 7.
Задача 8.
Оцените информационный объем следующего предложения:
Тяжело в ученье – легко в бою!
Так как каждый символ кодируется одним байтом, нам только нужно подсчитать количество символов, но при этом не забываем считать знаки препинания и пробелы. Всего получаем 30 символов. А это означает, что информационный объем данного сообщения составляет 30 байтов или 30 * 8 = 240 битов.
Задачи на кодирование информации
Большая подборка задач разного типа на соотношение единиц измерения и передачу информации, на кодирование текстовой, графической, аналоговой информации и определение информационного объема файлов.
Задания могут быть использованы на уроках с 8 по 11 класс, в том числе и при подготовке к ЕГЭ.
Задания на соотношение единиц измерения информации
1. 2 25 бит – сколько Мбайт?
2. Найти значение Х из соотношения 4 2-х Кб=16Мб
3. Найти Х, при котором равны информационные объемы 32 х+3 килобайт и 256 х мегабайт.
Задания на использование формулы Хартли и применение вероятностного подхода к измерению информации
4. Сколько различных звуковых сигналов можно закодировать с помощью 8 бит?
5. Сколько нужно бит, чтобы закодировать алфавит из 64 символов?
6. Когда Вы подошли к светофору, горел желтый свет. Затем зажегся красный. Какой объем информации Вы получили в момент, когда зажегся красный?
7. Какое количество информации несет сообщение о том, что человек живет в первом или втором подъезде, если в доме 16 подъездов?
9. Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100 процентов, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определите информационный объем в байтах результатов наблюдений.
10. В велокроссе участвуют 779 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем сообщения (в байтах), записанного устройством, после того как промежуточный финиш прошли 280 велосипедистов?
11. Для передачи сигналов на флоте используются специальные сигнальные флаги, вывешиваемые в одну линию (последовательность важна). Какое количество различных сигналов может передать корабль при помощи трех сигнальных флагов, если на корабле имеются флаги четырех различных видов (флагов каждого вида неограниченное количество)?
12. Каждый элемент светового табло может гореть одним из 4 цветов. Какое наименьшее количество элементов должно работать, чтобы можно было передать 500 различных сигналов?
13. Азбука Морзе позволяет кодировать символы для радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать, используя код Морзе длиной не менее пяти и не более шести сигналов (точек и тире)?
14. Некоторое сигнальное устройство за одну секунду передает один из трех специальных сигналов. Какое количество различных сообщений можно передать при помощи этого устройства за четыре секунды?
15. Одна ячейка памяти «троичной ЭВМ» (компьютера, основанного на использовании троичной системы счисления) может принимать одно из трех возможных состояний. Для хранения некоторой величины отвели 6 ячеек памяти. Сколько различных значений может принимать эта величина?
16. В ящике белые и черные шары. Черных среди них 2. Сообщение о том, что достали черный, несет 4 бита информации. Сколько белых шаров в ящике?
17. К празднику надували белые и синие шарики. Белых шариков 24. Сообщение о том, что лопнул синий шарик, несет 2 бита информации. Сколько всего надули шариков?
18. Два исполнителя Шалтай и Болтай проставляют 0 и 1 в каждую из имеющихся в их распоряжении клеточку. Шалтай может закодировать 512 символов и у него на две клеточки больше, чем у Болтая. Сколько клеток в распоряжении у Болтая?
20. Учитель, выставляя в журнал четвертные оценки по биологии за третью четверть (3, 4, 5), обратил внимание, что комбинация из трех четвертных оценок по этому предмету у всех учеников различна. Какое может быть максимальное количество учеников в этом классе?
21. В ящике находится 32 теннисных мяча, среди которых есть мячи желтого цвета. Наудачу вынимается один мяч. Сообщение «извлечен мяч НЕ желтого цвета» несет 4 бита информации. Сколько желтых мячей в ящике?
22. В некоторой стране автомобильный номер длиной 6 символов составляют из заглавных букв (задействовано 30 различных букв) и десятичных цифр в любом порядке. Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объем памяти в байтах, отводимый этой программой для записи 50 номеров.
23. Программа генерирует N-символьные пароли следующим образом: в качестве символов используются десятичные цифры, а также строчные и прописные латинские буквы в любом порядке (в латинском алфавите 26 знаков). Все символы кодируются одним и тем же минимально возможным количеством бит и записываются на диск. Программа сгенерировала 128 паролей и записала их в файл подряд, без дополнительных символов. Размер полученного файла составил 1,5 Кбайта. Какова длина пароля (N)?
24. В ящике лежат красные, белые и черные кубики. Сообщение о том, что достали красный кубик, несет 5 бит информации. Вероятность извлечения черного кубика в 2 раза больше, чем красного. Сколько информации несет сообщение об извлечении черного кубика?
25. Склад сети магазинов Медиамания получил от поставщика партию телевизоров, компьютеров и музыкальных центров. Из них 27 телевизоров. Для проверки качества поступившей аппаратуры товаровед случайным образом выбирает одну из поступивших на склад коробок. Информационный объем сообщения «Для проверки выбран не телевизор» равен 4- log2 7 бит. Количество информации в сообщении «Для проверки выбран не компьютер» равно log2 3-1 бит. Найти количество поступивших на склад компьютеров.
26. Злой экзаменатор никогда не ставит пятерок по информатике. По причине своей зловредности он заранее определил количество отметок каждого вида и произвольно расставил их абитуриентам. Количество информации, содержащееся в сообщении «Абитуриент Иванов не провалился на экзамене», равно log2 3 бит. Информационный объем сообщения «Абитуриент Сидоров получил тройку» равен двум битам. 22 абитуриента получили двойку или тройку. Найти количество абитуриентов, сдавших информатику.
Задачи на кодирование текстовой информации и определение объема текстового файла
27. Считая, что каждый символ кодируется одним байтом, определите, чему равен информационный объем в битах следующего высказывания Жан-Жака Руссо: Тысячи путей ведут к заблуждению, к истине – только один.
28. Определить объем памяти в Кбайтах, занимаемый текстом из 60 страниц по 512 символов на каждой странице. (кодировка ASCII)
29. Сообщение занимает 3 страницы и содержит 7950 байтов информации. Сколько строк на странице, если символов в каждой строке 25 и использована кодировка Unicode?
30. Определить максимальное количество страниц текста, содержащего по 80 символов в каждой строке и 64 строки на странице, которое может содержать файл, сохраненный на гибком магнитном диске объемом 10Кбайт. (кодировка ASCII)
31. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в коде Windows-1251, в кодировку Unicode. При этом информационное сообщение увеличилось на 400 бит. Какова длина сообщения в символах?
32. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16–битном коде Unicode, в 8–битную кодировку Windows–1251, при этом информационный объем сообщения составил 60 байт. Определите информационный объем в битах сообщения до перекодировки.
33. Два текста содержат одинаковое количество символов. Первый текст составлен в алфавите мощностью 8 символов, второй – 16 символов. Во сколько раз отличается количество информации в этих текстах?
34. Информационное сообщение объемом 1,5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, с помощью которого было записано сообщение?
35. Сколько символов содержит сообщение, написанное с помощью 16-символьного алфавита, если объем его составил 3/16 Кбайта?
36. В алфавите некоторого языка всего две буквы А и Б. Все слова этого языка состоят из 11 букв. Каков максимальный словарный запас этого языка?
37. Два сообщения содержат одинаковое количество информации. Количество символов в первом тексте в 2,5 раза меньше, чем во втором. Сколько символов содержат алфавиты, с помощью которых записаны сообщения, если известно, что размер каждого алфавита не превышает 32 символов и на каждый символ приходится целое число битов?
38. Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации в байтах содержит 5 страниц текста?
39. В языке некоторого племени всего 16 букв. Все слова состоят из 5 букв, всего в языке 8000 слов. Сколько памяти в байтах потребуется для хранения всех слов этого языка?
40. В некоторой кодировке слово из 20 букв занимает на 42 байта больше, чем слово из шести букв. Сколько бит отводится на одну букву, если под все символы этой кодировки отводится равный объем памяти?
41. Текст, записанный с помощью 16-ти символьного алфавита, занимает 10 полных секторов на односторонней дискете объемом 180 Кбайт. Дискета разбита на 40 дорожек по 9 секторов. Сколько символов содержит этот текст?
42. Система оптического распознавания символов позволяет преобразовывать отсканированные изображения страниц документа в текстовый формат со скоростью 4 страницы в минуту и использует алфавит мощностью 256 символов. Какое количество информации в байтах будет нести текстовый документ после 5 минут работы приложения, страницы которого содержат 40 строк по 50 символов?
Задания на кодирование графической информации и определение объема графического файла
43. Для хранения изображения размером 128128 точек выделено 4 Кбайт памяти. Определите, какое максимальное число цветов в палитре
44. 16-цветный рисунок содержит 500 байт информации. Из скольких точек он состоит?
45. Определить требуемый объем (в мегабайтах) видеопамяти для реализации графического режима монитора с разрешающей способностью 1024×768 пикселей при количестве отображаемых цветов 4 294 967 296.
46. Определить объем видеопамяти в Кбайтах для графического файла размером 1240480 пикселей и глубиной цвета 16 бит
47. Определить объем видеопамяти в Килобайтах для графического файла размером 640480 пикселей и палитрой из 32 цветов
48. После преобразования графического изображения количество цветов уменьшилось с 256 до 32. Во сколько раз уменьшился объем занимаемой им памяти?
49. Цветной сканер имеет разрешение 1024512 точек на дюйм. Объем памяти, занимаемой просканированным изображением размером 24 дюйма, составляет около 8 Мбайт. Какова выраженная в битах глубина представления цвета сканера?
50. Цвет пикселя, формируемого принтером, определяется тремя составляющими: голубой, пурпурной и желтой. Под каждую составляющую одного пикселя отвели по 4 бита. В какое количество цветов можно раскрасить пиксель?
51. Цвет пикселя монитора определяется тремя составляющими: зеленой, синей и красной. Под красную и синюю составляющие отвели по 5 бит. Сколько бит отвели под зеленую составляющую, если растровое изображение размером 88 пикселей занимает 128 байт?
52. После преобразования растрового 256-цветного графического файла в черно-белый двуцветный формат его размер уменьшился на 70 байт. Каков был размер исходного файла в байтах?
53. В процессе преобразования растрового графического файла его объем уменьшился в 1,5 раза. Сколько цветов было в палитре первоначально, если после преобразования получено изображение того же разрешения в 256-цветной палитре?
54. Фотография размером 1010 см была отсканирована с разрешением 400 dpi при глубине цвета 24 бита. Определите информационную емкость полученного растрового файла в килобайтах. Примечание: принять 1 дюйм = 2,5 см
56. В цветовой модели RGB графического редактора Paint.NET установлены следующие десятичные параметры цвета: 127, 127, 127. Какой цвет будет соответствовать этим параметрам?
Задания на кодирование аналоговой информации и определение объема звукового файла
57. Определить информационный объем в Кбайтах моноаудиофайла длительностью звучания 8 сек при глубине звука 8 бит и частоте 8 кГц
58. Определить длительность звучания стереоаудиофайла, занимающего 468,75 Кбайт памяти при глубине звука 16 бит и частоте 48 кГц
59. Музыкальная запись выполнена в формате CDDA (частота дискретизации 44100 Гц, 16 бит, стерео) и имеет продолжительность 19 мин 20 cек. Сколько секунд займет передача этой записи по каналу с пропускной способностью 16000 байт/сек?
60. При переводе в дискретную форму аналогового сигнала длительностью 2 мин 8 сек использовалась частота дискретизации 32 Гц и 16 уровней дискретизации. Найти в байтах размер полученного кода аналогового сигнала.
Задания на передачу информации по каналам связи и определение информационного объема файлов разных типов
61. Скорость передачи данных через ADSL-соединение равна 1240 Кбит/cек. Через данное соединение в течение 2 секунд передают файл. Определите размер файла в килобайтах.
62. Скорость передачи данных через ADSL-соединение равна 1024 000 бит/c. Через данное соединение передают файл размером 2500 Кбайт. Определите время передачи файла в секундах.
63. Пользователь компьютера, хорошо владеющий навыками ввода информации с клавиатуры, может вводить в минуту 100 знаков. Мощность алфавита, используемого в компьютере, равна 256. Какое количество информации в битах может ввести пользователь в компьютер за 1 минуту?
64. В течение 5 секунд было передано сообщение объемом 375 байт. Каков размер алфавита, с помощью которого оно было записано, если скорость передачи 200 символов в секунду?
65. Алфавит некоторого языка состоит из 32 символов. За сколько секунд можно передать текст из 1600 оптимального закодированных символов этого алфавита при скорости передачи 100 байт/сек
66. Сколько секунд потребуется модему, передающему сообщения со скоростью 28 800 бит/сек, чтобы передать цветное растровое изображение размером 800600 пикселей при условии, что цвет пикселя кодируется тремя байтами?
67. Сколько минут потребуется модему, передающему сообщения со скоростью 51200 бит/сек, чтобы передать цветное растровое изображение размером 800600 пикселей при условии, что в палитре около 4 миллиардов цветов?
68. Вычислить объем видеофайла (в Гбайтах) длительностью 64 сек, скоростью смены кадров равной 32 кадров/сек, разрешении 1280*640 точек и разрядностью цвета 16 бит. Объемом звуковой составляющей видеоклипа можно пренебречь.
69. Модем, передающий информацию со скоростью 16 384 бит/сек, передал цветное растровое изображение за 4 мин 16 сек. Укажите максимальное число цветов в палитре изображения, если известно, что его размер составил 1024512 пикселей.
70. Документ состоит из текстовой и графической информации. Текст содержит 30 строк по 30 символов в каждой в кодировке ASCII. Размер черно-белого изображения составляет 120300 точек. Определить информационный объем этого изображения в байтах.
71. Документ содержит несколько страниц текста, на каждой 60 строк по 30 символов в кодировке КОИ-8, и две иллюстрации размером 120*240 пикселей, в каждом изображении используется не более 8 различных цветов. Модем, работающий со скоростью передачи 28800 бит/сек, передал этот документ за 8 сек. Определите, сколько страниц в тексте.
72. Текст подготовлен для передачи по сети и содержит 51200 символов. Каждый символ кодируется двумя байтами и во избежание искажений передается трижды. Время передачи текста составило 64 секунды. Определите скорость передачи в байт/сек.
73. Данные объемом 16 Мбайт поступают на компьютер по линии со скоростью передачи данных 32 Мбит/сек. После получения 4 Мбайт компьютер начинает одновременно передавать эти данные по другой линии связи со скоростью 4 Мбит/сек. Сколько секунд пройдет от начала приема данных по высокоскоростному каналу до полной передачи их по низкоскоростному каналу?
74. У Оли есть доступ к сети Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения информации 221 бит в секунду. У Маши нет скоростного доступа в Интернет, но есть возможность получать информацию от Оли по низкоскоростному телефонному каналу со средней скоростью 213 бит в секунду. Маша договорилась с Олей, что та будет скачивать для нее данные объемом 8 Мбайт по высокоскоростному каналу и ретранслировать их Маше по низкоскоростному каналу. Компьютер Оли может начать ретрансляцию данных не раньше, чем им будет получен 1 Мбайт этих данных. Сколько Кбайт успеет скачать Маша к моменту окончания скачивания информации Олей?
75. Книга, состоящая из 1360 страниц, занимает 40 Мбайт. Часть страниц книги является цветными изображениями в формате 320640 точек. На одной странице книги с текстом размещается 1024 символа. Символы закодированы кодировкой ASCII. Количество страниц с текстом на 560 больше количества страниц с изображениями. Сколько цветов используется в палитре изображений?
Какое количество бит содержит слово корова
Прежде, чем рассматривать выполнение машинных программ аппаратурой ЭВМ, рассмотрим представление в памяти машины чисел, а также алфавитно-цифровых символов. Это представление потребуется нам в дальнейшем при изучении машинных программ, а также обрабатываемых ими данных.
1.1 Двоичные числа
Чтобы сделать вычислительные системы более надежными и простыми, их аппаратура строится из простейших электронных схем, которые могут находиться только в двух состояниях. Одно из них обозначается 0, а другое – 1. Такая схема предназначена для длительного или краткого хранения самой мелкой единицы информации – бита (от «BInary digiT» – двоичная цифра).
Любое число можно представить в виде цепочки битов. Такое представление числа называется двоичным числом. Цепочка из восьми битов называется байтом (рис. 1).

старший бит (бит 7) младший бит (бит 0)
Рис. 1. Пример байта
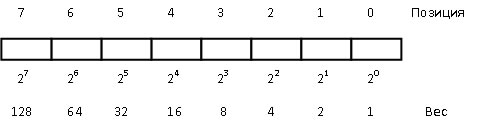
Величина двоичного числа определяется относительной позицией каждого бита и его значением. Позиционный вес младшего бита 2 о = 1(10), где 1(10) – единица в десятичной системе счисления. Следующий бит имеет вес 2 1 = 2(10). Вес любой позиции получается удвоением веса предыдущей позиции (рис. 2).
Рис. 2. Веса позиций байта
Для преобразования десятичного числа в двоичное можно использовать один из двух методов – метод деления и метод вычитания. Первый из этих методов широко используется в программах, выполняющих преобразование чисел из одной системы счисления в другую. Этот метод будет рассмотрен нами в других разделах, при описании соответствующих программ. Сейчас мы будем использовать метод вычитания, главное достоинство которого – наглядность. Согласно этому методу, для преобразования десятичного числа в двоичное надо сделать ряд вычитаний, каждое из которых даст значение одного бита.
Записывая 0 в остальные позиции битов (биты 0,2,3) получаем окончательный результат: 110010.
Для выполнения обратного преобразования следует сложить десятичные веса тех позиций, в которых стоит 1:
32 (бит 5) + 16 (бит 4) + 2 (бит 1) = 50
Байт может представлять десятичные положительные числа от 0 (00000000) до 255 (11111111). Число 255 может быть получено двумя способами: 1) суммированием весов всех битов байта; 2) по формуле 2 8 – 1, где 8 – номер первого бита, не вошедшего в состав байта.
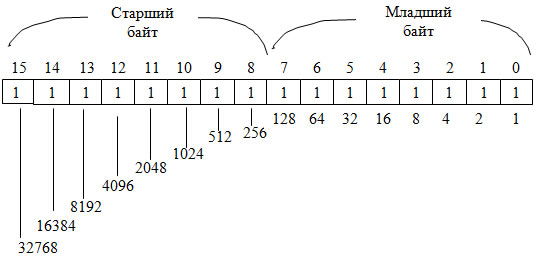
Машинным словом будем называть битовую строку длиной 16 битов. Одно слово содержит 2 байта (рис. 3). Каждый бит слова имеет свой вес. Просуммировав все веса, найдем максимальное целое число без знака, которое можно записать в одно слово, оно равно 2 16 – 1 = 65535.
Двоичное содержимое байта или слова может рассматриваться (интерпретироваться) как число без знака и как число со знаком. Число без знака занимает все 16 битов слова или 8 битов байта. Оно может быть только положительным. Просуммируем два таких числа:
Обратим внимание, что единица, появившаяся в старшем бите результата, свидетельствует лишь о возросшей величине результата, который для беззнаковых чисел может быть только неотрицательным.
Рис. 3. Веса позиций слова
все биты числа (в том числе и знаковый) инвертируются;
к полученному числу прибавляется 1.
Например, получим дополнительный код числа –65:
Для получения абсолютного значения отрицательного числа повторяют эти же самые два действия. Например:
Сумма +65 и –65 должна составить ноль:
В данном примере у нас произошли два интересных переноса: 1) в знаковый (7-й) разряд; 2) за пределы байта. Первая единица переноса обрабатывается как обычно, а вторая теряется. Оба переноса считаются правильными.
Отсюда видно, что нулевые биты в отрицательном двоичном числе фактически определяют его величину: рассмотрите весовые значения нулевых битов так, как если бы это были единичные биты, сложите эти значения и прибавьте 1.