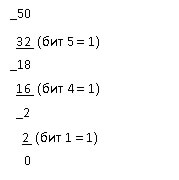какое количество бит содержит слово часы
Информатика. 7 класс
Конспект урока
Единицы измерения информации
Перечень вопросов, рассматриваемых в теме:
Каждый символ информационного сообщения несёт фиксированное количество информации.
Единицей измерения количества информации является бит – это наименьшаяединица.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Формулы, которые используются при решении типовых задач:
Информационный объём сообщения определяется по формуле:
I – объём информации в сообщении;
К – количество символов в сообщении;
i – информационный вес одного символа.
Теоретический материал для самостоятельного изучения.
Любое сообщение несёт некоторое количество информации. Как же его измерить?
Одним из способов измерения информации является алфавитный подход, который говорит о том, что каждый символ любого сообщения имеет определённый информационный вес, то есть несёт фиксированное количество информации.
Сегодня на уроке мы узнаем, чему равен информационный вес одного символа и научимся определять информационный объём сообщения.
Что же такое символ в компьютере? Символом в компьютере является любая буква, цифра, знак препинания, специальный символ и прочее, что можно ввести с помощью клавиатуры. Но компьютер не понимает человеческий язык, он каждый символ кодирует. Вся информация в компьютере представляется в виде нулей и единичек. И вот эти нули и единички называются битом.
Информационный вес символа двоичного алфавита принят за минимальную единицу измерения информации и называется один бит.
Эту формулу можно применять для вычисления информационного веса одного символа любого произвольного алфавита.
Алфавит древнего племени содержит 16 символов. Определите информационный вес одного символа этого алфавита.
Составим краткую запись условия задачи и решим её:
Информационный вес одного символа этого алфавита составляет 4 бита.
Сообщение состоит из множества символов, каждый из которых имеет свой информационный вес. Поэтому, чтобы вычислить объём информации всего сообщения, нужно количество символов, имеющихся в сообщении, умножить на информационный вес одного символа.
Математически это произведение записывается так: I = К · i.
Например: сообщение, записанное буквами 32-символьного алфавита, содержит 180 символов. Какое количество информации оно несёт?
I = 180 · 5 = 900 бит.
Итак, информационный вес всего сообщения равен 900 бит.
В алфавитном подходе не учитывается содержание самого сообщения. Чтобы вычислить объём содержания в сообщении, нужно знать количество символов в сообщении, информационный вес одного символа и мощность алфавита. То есть, чтобы определить информационный вес сообщения: «сегодня хорошая погода», нужно сосчитать количество символов в этом сообщении и умножить это число на восемь.
I = 23 · 8 = 184 бита.
Значит, сообщение весит 184 бита.
Как и в математике, в информатике тоже есть кратные единицы измерения информации. Так, величина равная восьми битам, называется байтом.
Бит и байт – это мелкие единицы измерения. На практике для измерения информационных объёмов используют более крупные единицы: килобайт, мегабайт, гигабайт и другие.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Итак, сегодня мы узнали, что собой представляет алфавитный подход к измерению информации, выяснили, в каких единицах измеряется информация и научились определять информационный вес одного символа и информационный объём сообщения.
Материал для углубленного изучения темы.
Как текстовая информация выглядит в памяти компьютера.
Набирая текст на клавиатуре, мы видим привычные для нас знаки (цифры, буквы и т.д.). В оперативную память компьютера они попадают только в виде двоичного кода. Двоичный код каждого символа, выглядит восьмизначным числом, например 00111111. Теперь возникает вопрос, какой именно восьмизначный двоичный код поставить в соответствие каждому символу?
Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код ‑ просто порядковый номер символа в двоичной системе счисления.
Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.Таблица для кодировки – это «шпаргалка», в которой указаны символы алфавита в соответствии порядковому номеру. Для разных типов компьютеров используются различные таблицы кодировки.
Таблица ASCII (или Аски), стала международным стандартом для персональных компьютеров. Она имеет две части.
В этой таблице латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Это правило соблюдается и в других таблицах кодировки и называется принципом последовательного кодирования алфавитов. Благодаря этому понятие «алфавитный порядок» сохраняется и в машинном представлении символьной информации. Для русского алфавита принцип последовательного кодирования соблюдается не всегда.
Запишем, например, внутреннее представление слова «file». В памяти компьютера оно займет 4 байта со следующим содержанием:
01100110 01101001 01101100 01100101.
А теперь попробуем решить обратную задачу. Какое слово записано следующим двоичным кодом:
01100100 01101001 01110011 01101011?
В таблице 2 приведен один из вариантов второй половины кодовой таблицы АSСII, который называется альтернативной кодировкой. Видно, что в ней для букв русского алфавита соблюдается принцип последовательного кодирования.
Вывод: все тексты вводятся в память компьютера с помощью клавиатуры. На клавишах написаны привычные для нас буквы, цифры, знаки препинания и другие символы. В оперативную память они попадают в форме двоичного кода.
Из памяти же компьютера текст может быть выведен на экран или на печать в символьной форме.
Сейчас используют целых пять систем кодировок русского алфавита (КОИ8-Р, Windows, MS-DOS, Macintosh и ISO). Из-за количества систем кодировок и отсутствия одного стандарта, очень часто возникают недоразумения с переносом русского текста в компьютерный его вид. Поэтому, всегда нужно уточнять, какая система кодирования установлена на компьютере.
Разбор решения заданий тренировочного модуля
№1. Определите информационный вес символа в сообщении, если мощность алфавита равна 32?
№2. Выразите в килобайтах 2 16 байтов.
2 6 = 64, а 2 10 байт – это 1 Кб. Значит, 64 · 1 = 64 Кб.
№3. Тип задания: выделение цветом
8 х = 32 Кб, найдите х.
Какое количество бит содержит слово часы
Для информации существуют свои единицы измерения информации. Если рассматривать сообщения информации как последовательность знаков, то их можно представлять битами, а измерять в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах и петабайтах.
Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.
Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.
Байт – основная единица измерения количества информации.
Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.
Производные единицы измерения количества информации
1 килобайт (Кб)=1024 байта =2 10 байтов
1 мегабайт (Мб)=1024 килобайта =2 10 килобайтов=2 20 байтов
1 гигабайт (Гб)=1024 мегабайта =2 10 мегабайтов=2 30 байтов
1 терабайт (Гб)=1024 гигабайта =2 10 гигабайтов=2 40 байтов
Методы измерения количества информации
Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:
Алфавитный подход к измерению количества информации
При этом подходе отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка, т.е. его алфавит можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет в себе каждый символ:
Вероятностный подход к измерению количества информации
Этот подход применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:
I – количество информации,
N – количество возможных событий,
Pi – вероятность i-го события.
Задача 1.
Шар находится в одной из четырех коробок. Сколько бит информации несет сообщение о том, в какой именно коробке находится шар.
Имеется 4 равновероятных события (N=4).
По формуле Хартли имеем: 4=2 i . Так как 2 2 =2 i , то i=2. Значит, это сообщение содержит 2 бита информации.
Задача 2.
Чему равен информационный объем одного символа русского языка?
В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа. I=log2 N=log2 32=5 битов (2 5 =32).
Примечание. Если невозможно найти целую степень числа, то округление производится в большую сторону.
Задача 3.
Чему равен информационный объем одного символа английского языка?
Задача 4.
Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний (“включено” или “выключено”). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 N сигналов.
2 5 6 , поэтому пяти лампочек недостаточно, а шести хватит. Значит, нужно 6 лампочек.
Задача 5.
Метеостанция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
В данном случае алфавитом является множество чисел от 0 до 100, всего 101 значение. Поэтому информационный объем результатов одного измерения I=log2101. Но это значение не будет целочисленным, поэтому заменим число 101 ближайшей к нему степенью двойки, большей, чем 101. это число 128=2 7 . Принимаем для одного измерения I=log2128=7 битов. Для 80 измерений общий информационный объем равен 80*7 = 560 битов = 70 байтов.
Задача 6.
Определите количество информации, которое будет получено после подбрасывания несимметричной 4-гранной пирамидки, если делают один бросок.
Пусть при бросании 4-гранной несимметричной пирамидки вероятности отдельных событий будут равны: p1=1/2, p2=1/4, p3=1/8, p4=1/8.
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
Задача 7.
Задача 8.
Оцените информационный объем следующего предложения:
Тяжело в ученье – легко в бою!
Так как каждый символ кодируется одним байтом, нам только нужно подсчитать количество символов, но при этом не забываем считать знаки препинания и пробелы. Всего получаем 30 символов. А это означает, что информационный объем данного сообщения составляет 30 байтов или 30 * 8 = 240 битов.
Какое количество бит содержит слово часы
Прежде, чем рассматривать выполнение машинных программ аппаратурой ЭВМ, рассмотрим представление в памяти машины чисел, а также алфавитно-цифровых символов. Это представление потребуется нам в дальнейшем при изучении машинных программ, а также обрабатываемых ими данных.
1.1 Двоичные числа
Чтобы сделать вычислительные системы более надежными и простыми, их аппаратура строится из простейших электронных схем, которые могут находиться только в двух состояниях. Одно из них обозначается 0, а другое – 1. Такая схема предназначена для длительного или краткого хранения самой мелкой единицы информации – бита (от «BInary digiT» – двоичная цифра).
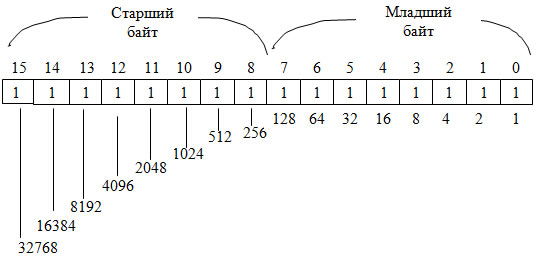
Любое число можно представить в виде цепочки битов. Такое представление числа называется двоичным числом. Цепочка из восьми битов называется байтом (рис. 1).

старший бит (бит 7) младший бит (бит 0)
Рис. 1. Пример байта
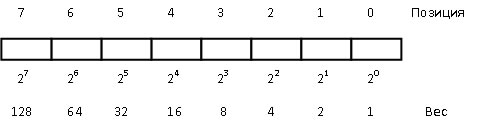
Величина двоичного числа определяется относительной позицией каждого бита и его значением. Позиционный вес младшего бита 2 о = 1(10), где 1(10) – единица в десятичной системе счисления. Следующий бит имеет вес 2 1 = 2(10). Вес любой позиции получается удвоением веса предыдущей позиции (рис. 2).
Рис. 2. Веса позиций байта
Для преобразования десятичного числа в двоичное можно использовать один из двух методов – метод деления и метод вычитания. Первый из этих методов широко используется в программах, выполняющих преобразование чисел из одной системы счисления в другую. Этот метод будет рассмотрен нами в других разделах, при описании соответствующих программ. Сейчас мы будем использовать метод вычитания, главное достоинство которого – наглядность. Согласно этому методу, для преобразования десятичного числа в двоичное надо сделать ряд вычитаний, каждое из которых даст значение одного бита.
Записывая 0 в остальные позиции битов (биты 0,2,3) получаем окончательный результат: 110010.
Для выполнения обратного преобразования следует сложить десятичные веса тех позиций, в которых стоит 1:
32 (бит 5) + 16 (бит 4) + 2 (бит 1) = 50
Байт может представлять десятичные положительные числа от 0 (00000000) до 255 (11111111). Число 255 может быть получено двумя способами: 1) суммированием весов всех битов байта; 2) по формуле 2 8 – 1, где 8 – номер первого бита, не вошедшего в состав байта.
Машинным словом будем называть битовую строку длиной 16 битов. Одно слово содержит 2 байта (рис. 3). Каждый бит слова имеет свой вес. Просуммировав все веса, найдем максимальное целое число без знака, которое можно записать в одно слово, оно равно 2 16 – 1 = 65535.
Двоичное содержимое байта или слова может рассматриваться (интерпретироваться) как число без знака и как число со знаком. Число без знака занимает все 16 битов слова или 8 битов байта. Оно может быть только положительным. Просуммируем два таких числа:
Обратим внимание, что единица, появившаяся в старшем бите результата, свидетельствует лишь о возросшей величине результата, который для беззнаковых чисел может быть только неотрицательным.
Рис. 3. Веса позиций слова
все биты числа (в том числе и знаковый) инвертируются;
к полученному числу прибавляется 1.
Например, получим дополнительный код числа –65:
Для получения абсолютного значения отрицательного числа повторяют эти же самые два действия. Например:
Сумма +65 и –65 должна составить ноль:
В данном примере у нас произошли два интересных переноса: 1) в знаковый (7-й) разряд; 2) за пределы байта. Первая единица переноса обрабатывается как обычно, а вторая теряется. Оба переноса считаются правильными.
Отсюда видно, что нулевые биты в отрицательном двоичном числе фактически определяют его величину: рассмотрите весовые значения нулевых битов так, как если бы это были единичные биты, сложите эти значения и прибавьте 1.
1 символ это сколько бит
Я просто смущен. сколько символов в одном бите?
Это зависит от характера и того, в каком кодировании он находится:
Символ ASCII в 8-разрядной кодировке ASCII составляет 8 бит (1 байт), хотя он может поместиться в 7 бит.
Символ ISO-8895-1 в кодировке ISO-8859-1 составляет 8 бит (1 байт).
Символ Unicode в кодировке UTF-8 находится между 8 битами (1 байт) и 32 битами (4 байта).
Символ Юникода в кодировке UTF-16 находится между 16 (2 байтами) и 32 битами (4 байта), хотя большинство общих символов принимают 16 бит. Это кодировка, используемая Windows внутренне.
Символ Unicode в кодировке UTF-32 всегда 32 бита (4 байта).
Символ ASCII в UTF-8 — 8 бит (1 байт), а в UTF-16 — 16 бит.
Дополнительные символы (не ASCII) в ISO-8895-1 (0xA0-0xFF) будут принимать 16 бит в UTF-8 и UTF-16.
Это означало бы, что между 0.03125 и 0.125 символами.
Один бит это 1/8 (одна восьмая или 0.125 символа). Из учебника информатики мы знаем что для того чтобы записать один символ нам нужен 1 байт, который состоит из 8 бит, отсюда 1 бит это 1/8 символа или 0.125 символа. Почему 1 символ это байт? Все дело в том что машина (компьютер) не понимает наши буквы и символы, она понимает только значения «верно» и «ложь» которые записаны в двоичном коде (то есть при помощи двух символов 1 и 0). Соответственно для того чтобы закодировать один из 256 символов при помощи нолей и единиц нам потребуется восемь мест в каждом из которых может быть только один из двух вариантов: единица или ноль. Таким местом как раз и является один бит который может содержать только ноль или единицу, а вот последовательность из восьми нолей или единиц можно описать один из 256 символов. Таким образом и получается что для записи одного символа нам нужно 8 бит или один байт.
Сравнивая UTF-8 и UTF-16, можно отметить, что наибольший выигрыш в компактности UTF-8 даёт для текстов на латинице, поскольку латинские буквы без диакритических знаков, цифры и наиболее распространённые знаки препинания кодируются в UTF-8 лишь одним байтом, и коды этих символов соответствуют их кодам в ASCII. [4] [5]
Содержание
Алгоритм кодирования [ править | править код ]
Алгоритм кодирования в UTF-8 стандартизирован в RFC 3629 и состоит из 3 этапов:
1. Определить количество октетов (байтов), требуемых для кодирования символа. Номер символа берётся из стандарта Юникод.
| Диапазон номеров символов | Требуемое количество октетов |
|---|---|
| 00000000-0000007F | 1 |
| 00000080-000007FF | 2 |
| 00000800-0000FFFF | 3 |
| 00010000-0010FFFF | 4 |
Для символов Юникода с номерами от U+0000 до U+007F (занимающими один байт c нулём в старшем бите) кодировка UTF-8 полностью соответствует 7-битной кодировке US-ASCII.
2. Установить старшие биты первого октета в соответствии с необходимым количеством октетов, определённом на первом этапе:
Если для кодирования требуется больше одного октета, то в октетах 2-4 два старших бита всегда устанавливаются равными 102 (10xxxxxx). Это позволяет легко отличать первый октет в потоке, потому что его старшие биты никогда не равны 102.
| Количество октетов | Значащих бит | Шаблон |
|---|---|---|
| 1 | 7 | 0xxxxxxx |
| 2 | 11 | 110xxxxx 10xxxxxx |
| 3 | 16 | 1110xxxx 10xxxxxx 10xxxxxx |
| 4 | 21 | 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx |
3. Установить значащие биты октетов в соответствии с номером символа Юникода, выраженном в двоичном виде. Начать заполнение с младших битов номера символа, поставив их в младшие биты последнего октета, продолжить справа налево до первого октета. Свободные биты первого октета, оставшиеся незадействованными, заполнить нулями.
Примеры кодирования [ править | править код ]
| Символ | Двоичный код символа | UTF-8 в двоичном виде | UTF-8 в шестнадцатеричном виде | |
|---|---|---|---|---|
| $ | U+0024 | 100100 | 0 0100100 | 24 |
| ¢ | U+00A2 | 10 100010 | 110 00010 10 100010 | C2 A2 |
| € | U+20AC | 10 0000 10 101100 | 1110 0010 10 000010 10 101100 | E2 82 AC |
| �� | U+10348 | 1 0000 0011 01 001000 | 11110 000 10 010000 10 001101 10 001000 | F0 90 8D 88 |
Маркер UTF-8 [ править | править код ]
| 1-й байт | 2-й байт | 3-й байт | |
|---|---|---|---|
| Двоичный код | 1110 1111 | 1011 1011 | 1011 1111 |
| Шестнадцатеричный код | EF | BB | BF |