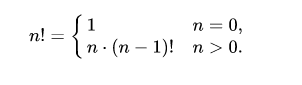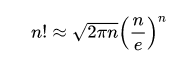Факториал отрицательного числа чему равен
Факториал
ЧТО ТАКОЕ ФАКТОРИАЛ
Для нахождения факториала нужно умножить все целые числа от выбранного нами числа до 1.
Факториал обозначается символом «!»
4! = 4 · 3 · 2 · 1 = 24
5! = 5 · 4 · 3 · 2 · 1 = 120
Обычно говорят 4! как «факториал четырех».
ВЫЧИСЛЕНИЕ ФАКТОРИАЛА
Можно легко рассчитать факториал, зная значение факториала предыдущего числа:
Можно это записать в виде таблицы:
| n | n! | ||
| 1 | 1 | 1 | 1 |
| 2 | 2 x 1 | = 2 x 1! | = 2 |
| 3 | 3 x 2 x 1 | = 3 x 2! | = 6 |
| 4 | 4 x 3 x 2 x 1 | = 4 x 3! | = 24 |
| 5 | 5 x 4 x 3 x 2 x 1 | = 5 x 4! | = 120 |
| 6 | и так далее | и так далее |
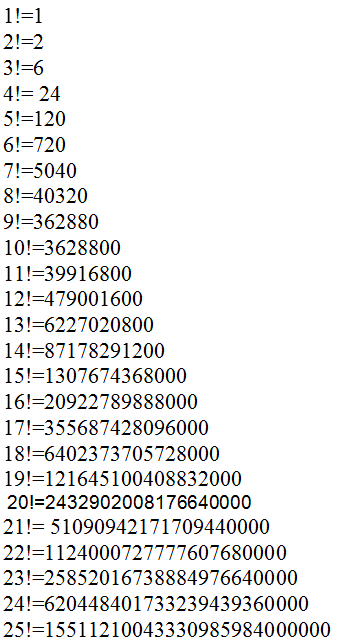
Для точного определения факториала любого числа следует воспользоваться таблицей факториалов
9! равно 362.880. Попробуйте посчитать 10!
10! = 9!х10
10! = 362.880 х 10 = 3.628.800
ФОРМУЛА ФАКТОРИАЛА
Существует правило как найти n факториал:
ФАКТОРИАЛ 0
Это очень интересная тема. Принято, что 0! = 1. А почему?
Никакое умножение чисел не приводит к 1, но давайте проследим факториалы в обратном порядке, скажем, от 4!:
И во многих задачах 0! = 1 просто имеет смысл.
ФАКТОРИАЛ ОТРИЦАТЕЛЬНОГО ЧИСЛА
Можем ли мы найти факториалы для чисел меньших нуля?
Нет. Факториалы для таких чисел не определены.
Почему? Легко объяснить на примере.
Начнем с 3! = 3 × 2 × 1 = 6 и спускаемся вниз:
2! = 3! / 3 = 6 / 3 = 2
1! = 2! / 2 = 2 / 2 = 1
0! = 1! / 1 = 1 / 1 = 1
(поэтому 0! = 1)
(−1)! = 0! / 0 = 1 / 0 = ой, деление на ноль не определено
И с этого момента все целочисленные факториалы не определены.
ФАКТОРИАЛ ДРОБНОГО ЧИСЛА
Можем ли мы найти факториалы для таких чисел, как 0,4 или −8,116?
Да мы можем! Но нам нужно углубиться в тему под названием Гамма-функция, которая выходит за рамки этой страницы.
И они могут быть отрицательными (кроме целых чисел).
Вот несколько значений дробных факториалов:
| (-1/2)! | √π |
| (1/2)! | (1/2)√π |
| (3/2)! | (3/4)√π |
| (5/2)! | (15/8)√π |
ПРИМЕНЕНИЕ ФАКТОРИАЛА
Факториалы незаменимы для вычисления количества перестановок, сочетаний и размещений.
Что такое 100! / 98!
Используя наши знания из предыдущего примера, мы можем сразу перейти к следующему:
100!/98! = 100 × 99 = 9900
Другие примеры задач с факториалом и их решение на странице решение факториалов.
ИНТЕРЕСНЫЕ ФАКТЫ
100 факториал: 100! приблизительно 9,3326215443944152681699238856 x 10 157
200 факториал: 200! приблизительно 7,8865786736479050355236321393 x 10 374
Факториал
Что такое факториал
Чтобы найти факториал числа, нужно умножить все целые числа от 1 до этого числа.
Рассчитать онлайн факториал любого числа можно на этом онлайн калькуляторе.
Факториал обозначается символом «!»
4! = 1 · 2 · 3 · 4 = 24
Выражение 5! = 120 читается так: «пять факториал равно 120» или «факториал пяти равен 120»
Расчет факториала от предыдущего значения
Мы можем легко вычислить факториал из факториала предыдущего числа.
Небольшая таблица для понимания
9! равняется 362880. Попробуйте посчитать 10!
10! = 10 × 9!
10! = 10 × 362880 = 3 628 800
Итак, правило такое:
«Чтобы получить факториал любого числа, нужно это число, умножить на факториал предыдущего числа »
Итак, 10! = 10 × 9!, … и 125! = 125 × 124!, и т. д.
Факториал нуля
А существует ли факториал нуля?
Принято считать, что 0! = 1. Таким образом, факториал нуля равен единице. Почему именно так, можно узнать, посетив страницу Факториалы.
Где используется факториал
Одна из областей, в которой факториал часто используется — это раздел математики, который называется комбинаторика, где нужно посчитать количество перестановок, размещений или сочетаний.
Сколько существует способов расположить буквы а,б,в,г без повторений.
Для одной буквы — это один способ — а (или 1! способов)
Для двух букв — два способа — аб, ба. (или 2! способов)
Для трех букв — шесть способов — абв, авб, бав, бва, ваб, вба (или 3! способов).
Для четырех букв — 24 или 4! способов (комбинации попробуйте сами)
Факториалы отрицательных чисел
Нет. Факториалы отрицательных целых чисел не определены. Если вам интересно, почему нельзя получить факториалы чисел, меньших нуля, посмотрите Почему нет факториалов отрицательных чисел.
Интересные факты о факториале
Шесть недель — ровно 10! секунд (= 3 628 800)
Есть 52! способа перемешать колоду карт.
Это 8,0658175 … × 10 67 способов
В наблюдаемой вселенной около 60! атомов.
Факториал числа n – это произведение чисел от 1 до n. Определён только для целых неотрицательных чисел. Формула факториала:
Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.
Это очень просто, вот пример:
Таблица факториалов
Свойства факториалов
Рекуррентная формула
Комбинаторная интерпретация
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга
Позволяет не перемножать большие числа. Обычно необходим только главный член:
Расчет по предыдущему значению
Функцию легко вычислить из предыдущего значения:
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.
Однако было решено, что в случае 0 результат будет равен 1.
Некоторые очень большие значения
Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.
Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.
Примеры вычисления факториалов больших чисел:
70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
200! это примерно 7 88657867867364479050355236321393 x 103743.
Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.
Программа на языке Паскаль:
На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.
Факториал определение, формула, обозначение, основные свойства и функции, таблица, алгоритмы нахождения, примеры задач с решениями, онлайн-калькулятор
Факториал числа n – это произведение чисел от 1 до n. Определён только для целых неотрицательных чисел.
Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.
Это очень просто, вот пример:
Факторизация — разложение функции на множители.
Таблица факториалов
Свойства факториалов
Рекуррентная формула
Комбинаторная интерпретация
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга
Позволяет не перемножать большие числа. Обычно необходим только главный член:
Расчет по предыдущему значению
Функцию легко вычислить из предыдущего значения:
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.
Однако было решено, что в случае 0 результат будет равен 1.
Некоторые очень большие значения
Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.
Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.
Примеры вычисления факториалов больших чисел:
70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
200! это примерно 7 88657867867364479050355236321393 x 103743.
Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.
Программа на языке Паскаль:
На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.
Факториал дроби (½) — это половина квадратного корня pi = (½)√π.
Примеры задач с решениями
Задание 1
Задание 2
Использование факториалов
Математика и многие ее области используют функцию. В комбинаторике функция была введена именно для расчета перестановки. Также понятие тесно связано с биномом ньютона (формула бинома Ньютона необходима для разложения степени (x + y) n в многочлен).
Факториал
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.
Последовательность факториалов неотрицательных целых чисел начинается так:
1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, … (последовательность A000142 в OEIS)
Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция 
Содержание
Свойства
Рекуррентная формула
Комбинаторная интерпретация
В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества <A,B,C,D> из 4-х элементов существует 4! = 24 перестановки:
Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, т. к. пустое множество упорядочено единственным способом.
Связь с гамма-функцией
Факториал связан с гамма-функцией от целочисленного аргумента соотношением:
Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.
Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при
Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как
Поскольку 

Формула Стирлинга
см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).
Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:
При этом можно утверждать, что
Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что
Разложение на простые числа
Каждое простое число p входит в разложение n! на простые множители в степени
Другие свойства
Обобщения
Двойной факториал

По определению полагают 0!! = 1.
Последовательность значений n!! начинается так:
1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, … (последовательность A006882 в OEIS).
Кратный факториал
Пусть число n представимо в виде 


Кратный факториал связан с гамма-функцией следующим соотношением [2] :
Убывающий факториал
Убывающим факториалом (или неполным факториалом) называется выражение
Возрастающий факториал
Возрастающим факториалом называется выражение
Праймориал или примориал
Праймориал или примориал (англ. primorial ) числа n обозначается n# и определяется как произведение всех простых чисел, не превышающих n. Например,
11# = 12# = 2 · 3 · 5 · 7 · 11 = 2310.
Последовательность праймориалов (включая 
1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, … (последовательность A002110 в OEIS).
Суперфакториалы
Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен
(поскольку устоявшегося обозначения нет, используется функциональное).
Последовательность суперфакториалов чисел n⩾0 начинается так:
1, 1, 2, 12, 288, 34 560, 24 883 200, … (последовательность A000178 в OEIS).
Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Superduperfactorial ), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел n⩾0 начинается так:
1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 125 411 328 000, 5 056 584 744 960 000, 1 834 933 472 251 084 800 000, 6 658 606 584 104 736 522 240 000 000, 265 790 267 296 391 946 810 949 632 000 000 000, 127 313 963 299 399 416 749 559 771 247 411 200 000 000 000 … (последовательность A055462 в OEIS)
где 

Субфакториал
Ссылки
См. также
Примечания
Полезное
Смотреть что такое «Факториал» в других словарях:
ФАКТОРИАЛ — [англ. factorial Словарь иностранных слов русского языка
ФАКТОРИАЛ — (обозначение «!»), число, получаемое в результате умножения данного числа на все целые числа меньше него. Например, факториал числа 6 равен 6!=6.5.4.3.2.1=720. Факториалом нуля считают 0!=1 … Научно-технический энциклопедический словарь
ФАКТОРИАЛ — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1?2. n; обозначается n! … Современная энциклопедия
факториал — сущ., кол во синонимов: 1 • термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Факториал — (от латинского factor деятель, создатель, множитель), произведение натуральных чисел от единицы до какого либо данного натурального числа n, т.е. 1´2´. ´n; обозначается n!. … Иллюстрированный энциклопедический словарь
ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного натурального числа n; обозначается n! = 1·2·3·. ·n; по определению, 0! = 1 … Большая политехническая энциклопедия
факториал — произведение натуральных чисел от единицы до какого либо данного натурального числа n, то есть 1·2·3·. ·n; обозначается: n!. Например, 5! = 1·2·3·4·5 = 120. * * * ФАКТОРИАЛ ФАКТОРИАЛ, произведение натуральных чисел от единицы до какого либо… … Энциклопедический словарь
факториал — faktorialas statusas T sritis fizika atitikmenys: angl. factorial vok. Faktorielle, f; Fakultät, f rus. факториал, m pranc. factorielle, f … Fizikos terminų žodynas