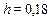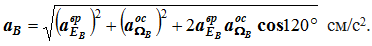Ускорение точки равно показать что точка движется по поверхности кругового конуса
Описание файла
Просмотр DJVU-файла онлайн
Найти нормальное ускорение точки, 1.45. Выразить орты сопровождающего трехгранника (т, и, Ь) через вектор скорости т и вектор ускорения я«точки, если я«х ч
З 2. Сложное движение точки 1.47. Найти кривизну траектории точки, движущейся с ускоре- т нием и = —,(г х г), где г ее радиус-вектор, 7 = сопв1, если в началь- г ный момент скорость точки равняласы’о. й 2. Сложное движение точки 2.1. В соревнованиях по ориентированию на местности п участников в начальный момент находятся на окружности радиуса Л на одинаковом расстоянии друг от друга.
Во время движения каждому из участников известен лишь пеленг соседа, который в начальной позиции был справа. Для того чтобы собраться на окружности радиуса г (г ( Л), участники ориентируют направление своей скорости по известному пеленгу. Найти время, через которое опи соберутся на заданной окружности, если каждый из них будет двигаться с постоянной скоростью ш 2.2.
2.3. Винт самолета, установленного на вибростенде, вращается с постоян- ) ной угловой скоростью оз относительно У горизонтальной оси М% (см. рисунок). А Ось МЮ перемещается параллельно самой себе в вертикальной плоскости зу по закону ОМ = аейпй
2.5. Полая трубка (см. рисунок), изогнутая в форме кругового кольца радиуса Л, вращается с постоянной угловой скоростью оз1 вокруг оси А В, укрепленной в рамке. Рамка в свою очередь вращается вокруг горизонтальной оси С11 с постоянной угловой скоростью еоз. 1. Кинематика и динамика 16 По трубке с постоянной относительной скоростью ие движется шарик. Найти скорость и ускорение шарика в положениях 1, 2, 3, 4 в момент, когда плоскость трубки совпадает с плоскостью рамки. К задаче 2.6 К задаче 2.5 2.6. Кабина для тренировки космонавтов (см. рисунок) вращается относительно горизонтальной оси 1 1, укрепленной в раме, которая в свою очередь вращается относительно вертикальной оси 2- 2. Угловые скорости вращения се1 и са2 относительно указанных осей постоянны.
Найти ускорение точки кабины, отстоящей от оси 1-1 на расстояние 1 и находящейся в начальный момент на оси 2-2, как функцию времени. 2.7. Горизонтальная плоскость лу вращается вокруг вертикальной оси Оз с постоянной угловой скоростью а. Из неподвижной точки О плоскости ху начинает движение точка М. Найти траекторию точки М отпосителын1 плоскости, если абсолютная скорость зг точки постоянна.
Найти также относительное ускорение ш„точки М в зависимости от ОМ = 1. Рассмотреть два случая: а) т а = О, б) т в
О. 2.8. Показать, что при сложном движении точки имеют место соотношения ч„= зг, +тге/2, те = тке+зке/2, где ч„ч„- переносная и относительная скорости; зг„зв„зг, переносное, относительное и кориолисово ускорения. 2.9. Найти условия, при которых в сложном движении точки справедливы соотношения те = тт,, те = тте.
2.10. Показать, что при сложном движении точки всегда справедливо тождество (т,. — те) = тт,. — зге. а1 з 2. Снежное движение точки 2.11. Призма АВС (см. рисунок) движется поступательно вдоль оси Ох с ускорением че, имея в данный момент скорость ч. По линии наиболыпего ската ВС призмы катится без скольжения цилиндр, скорость центра которого относительно призмы постоянна и равна чо. Радиус цилиндра Л, е’.ВСА = а. Найти скорости и ускорения точек 1, 2, 3, 4 цилиндра в данный момент времени. К задаче 2.11 К задаче 2.12 2.12.
Направляющая Ох вращается в горизонтальной плоскости вокруг точки О с постоянной угловой скоростью из (см. рисунок). В этой же плоскости относительно направляющей движется стержень А В с постоянной скоростью чо. Стержень образует прямой угол с направляющей. Найти зависимость скорости и ускорения точки В стержня от времени, если длина стержня равна 1 и в начальный момент точка А совпадала с точкой О.
2.13. На плече АВ центрифуги 1сьь рисунок) укреплена испытательная кабина, которая вращается вокруг горизонтальной оси 2 — 2, перпендикулярной вертикальной плоскости САВ. Угловые скорости цен- в трифуги ео1 (относительно оси 1 «1) К задаче 2.13 и кабины ез2 постоянны, длина плеча А В равна Л.
Кинематика и динамика 2.15. Стержень ОА (см. рисунок) вращается в горизонтальной плоскости относительно вертикальной оси Оз с постоянной угловой К задаче 2.15 К задаче 2.16 К задаче 2.14 скоростью оз. Колечко Р колеблется вдоль стержня по закону ОР = = а(1+ гйпеоо1). Найти скорость и ускорение колечка, пренебрегая его размерами. 2.16. Стержень ОА (см.
рисунок) совершает колебания в плоскости хд по закону
роашсо1. По стержню скользит колечко Р. Пренебрегая размерами колечка, найти его скорость и ускорение, если ОР = а1 /2. 2.17. Движение точки А в плоскости хд (см. рисунок) задано в полярных координатах г = г(1), оз =
р(1). Представляя движение точки А относительно плоскости хд как сложное: вместе с системой Осц (переносное) и относительно Огг1(относительное), найти проекции скорости и ускорения точки А на оси Ос и Оц. К задаче 2.18 К задаче 2.17 2.18.
Движение точки А (см. рисунок) задано в сферических координатах г = г(1), О = 6(1), оз =
Помощь в компьютерном наборе текста
Траекторией относительного движения точки М является прямая линия – образующая конуса; траекторией переносного движения является дуга окружности, по которой движется точка конуса, с которой в данный момент времени совпадает точка М.
Определим положение точки М на образующей конуса в данный момент времени, для этого подставим время t = cек в уравнение относительного движения Sr(t)
Sr = 80 (1– cos2 ) = 80(1– cos2600) = 80∙ = 60 cм.
Вычислим для данного положения точки величину абсолютной скорости ; для вычислений используем векторную формулу скорости абсолютного движения точки
Относительное движение точки задано естественным способом, поэтому величину относительной скорости находим по формуле
Вычислим при t = cек
Переносной скоростью точки М является скорость точки конуса, с которой в данный момент времени совпадает движущаяся точка М. Конус, вместе с которым точка М участвует в переносном движении, совершает вращение вокруг неподвижной оси, поэтому для вычисления переносной скорости точки воспользуемся формулой для определения скорости точки тела вращающегося вокруг неподвижной оси
Найдем величины R и ωе
R = Sr ∙ sin 300 = 60 ∙ 0,5 = 30 см,
тогда величина переносной скорости точки будет равна
Величину абсолютной скорости можно найти по теореме косинусов
при подстановке в нее полученных значений и определяем величину абсолютной скорости точки М
= 123,95 см/сек = 1,2395 м/сек,
Для определения абсолютного ускорения точки М воспользуемся формулой
где – вектор относительного ускорения, – вектор переносного ускорения, – вектор ускорения Кориолиса.
Относительное ускорение при задании движения естественным способом вычисляется по формуле
— касательная составляющая относительного ускорения
знак «–» говорит о том, что вектор ускорения направлен в сторону, противоположную направлению вектора относительной скорости ;
— нормальная составляющая относительного ускорения
Покажем на рисунке вектор
Переносным ускорением точки М является ускорение точки конуса, с которой в данный момент времени совпадает движущаяся точка М. Конус вращается вокруг неподвижной оси, поэтому переносное ускорение точки конуса (а, следовательно, и точки М) вычисляется по формуле
Величина нормальной составляющей переносного ускорения точки равна
Вычислим величину ускорения Кориолиса. Модуль ускорения Кориолиса находится по формуле
Как видно из рисунка угол = α = 300, значит = = 0,5. В результате получаем
= 2·2,5·96,68·0,5 = 241,7 см/сек2.
Направление вектора ускорения Кориолиса можно определить по правилу Жуковского, которое гласит, что для определения направления вектора ускорения Кориолиса следует проекцию вектора относительной скорости на плоскость перпендикулярную оси переносного вращения повернуть в этой же плоскости на угол 90о в направлении вращения.
Все найденные составляющие вектора абсолютного ускорения точки М изображены на рисунке 12.
Величину абсолютного ускорения можно найти:
— графически (для чего необходимо произвести на чертеже построения всех составляющих векторов в масштабе, найти их геометрическую сумму, измерить и с помощью масштаба определить величину результирующего вектора),
Из точки М проведем координатные оси x1, y1, z1 и найдем проекции на эти оси вектора абсолютного ускорения точки М (рисунок 13).
= = 187, 5 + 155,8∙0,5 = 265,4 см/сек2,
= = 155,8∙ 0,866 = 134,9 см/сек2.
Вычислим абсолютное ускорение точки М
= 334,1 см/сек2 = 3,341 м/сек2.
Ответ: величина абсолютной скорости = 123,95 см/сек = 1,2395 м/сек,
величина абсолютного ускорения = 334,1 см/сек2 = 3,341 м/сек2.
Описание файла
Просмотр DJVU-файла онлайн
8.38). Окружность вращается с постоянной угловой скоростью а вокруг вертикальной оси, совпадающей с диаметром окружности. Вычислить скорость центра масс стержня в тот момент, когда он расположен горизонтально (в начальный момент времени стержень покоился относительно окружности в вертикальном положении). 8.39. Вертикальная плоскость вращается с постоянной угловой скоростью си вокруг вертикальной оси. К оси прикреплен вершиной однородный круговой конус с углом 2сс при вершние и образую- Динамика твердого тела 1г. в щей длиной й В начальный момент времени ось конуса занимала горизонтальное положение, Предполагая, что плоскость абсолютно шероховатая, найти границы движения конуса (соприкасающегося с вращающейся плоскостью).
8.40. Один конец оси симметричного волчка закреплен, а другой скользит по гладкой вертикально расположенной окружности с центром в точке закрепления волчка. Эта окружность вращается вокруг вертикальной оси с постоянной угловой скоростью. Написать лагранжиан волчка и найти решение уравнений движения в квадратурах. 8.41. Симметричный волчок закреплен в одной точке. Расстояние от точки закрепления до центра масс волчка равно й Найти решение задачи, исследовать движение быстрого волчка, а также устойчивость волчка при его вращении вокруг вертикальной оси. 8.42.
Методом усреднения рассмотреть движение симметричного волчка с закрепленной точкой (кинетическая энергия волчка велика по сравнению с его потенциальной энергией). рис, ааа 8.43. Шарик движется по шероховатой горизонтальной поверхности, вращающейся вокруг вертикальной оси с постоянной угловой скоростью оз. Найти угловую скорость вращения шарика н закон движения его центра масс.
8.44. Тонкий однородный диск радиуса а катится по шероховатой’поверхности. Найти уравнения движения диска. Исследовать 61 Общий случай рвнженнв 4 З) условия устойчивости при движении диска по прямой линии. 8.45. Обруч радиуса а катится вдоль прямой линии по абсолютно шероховатой горизонтальной поверхности так, что его плоскость остается вертикальной; скорость центра масс обруча равна п, Показать, что при условии оа>1/4да движение обруча устойчиво и при небольших возмущениях его плоскость будет колебаться около вертикали с частотой т
8.46. Центр однородного тонкого диска массы т радиуса а скреплен с концом оси, перпендикулярной поверхности диска 1рис. 8.46). Другой конец оси (длина оси Ь) шарнирно закреплен на расстоянии а от горизонтальной шероховатой плоскости, по которой диск катится без проскальзывания, Найти реакции связей в точке а шарнирного закрепления оси и в точке Ь касания диска с плоскостью. 8.47. Центр масс симметричного спутника движется по окружности радиуса га вокруг Земли. Написать уравнения, определяющие положение спутника относительно плоскости орбиты и радиуса-вектора, проведенного из центра Земли в центр масс спутника.
9.2. Найти канонические уравнения материальной точки, движущейся в однородном гравитационном поле по гладкой сферической поверхности (радиус сферы изменястся по закону т=г(х)), 9.3. Записать уравнения Гамильтона для заряда в постоянном однородном магнитном поле и электрическом поле с потенциалом у. Получить интегралы движения в случае 9=0, 9.4. Рассматривая углы Эйлера в качестве обобщенных координат твердого тела с одной неподвижной точкой, получить функцию Гамильтона для этого тела.
Получить динамические уравнения Эйлера из уравнений Гамильтона. 9.5. Найти траекторию одномерного гармонического осциллятора в фазовом пространстве, 9.6. Показать, что уравнения Гамильтона можно записать в виде —.=(Р„Н), — =(фо Н) (з = 1. з), симметричном относительно канонических переменных’, 9.7.-Показать, что для функции /(с/, р, /) канонических переменных имеют место соотношения (ч, /) = —; (р„/) = — —. д/ д/ дрз ‘ » дух 9.8. Показать, что функция / = х — р//ш является интегралом движения свободной частицы в отсутствие внешних сил. 9 9.
Доказать, что скобки Пуассона а) (М,р’) = О; б) (М,г’) = О. ‘ Здесь н далее длд скобки Пуассона от фуикии» /
и /х канонических переменных нсподьзуетсд обозначение (/ь /х). 4 1) Канонические у авнения Скобки Пуассона 9.10 С помощью скобок Пуассона показать, что импульс Р системы является интегралом движения, если ее гамильтониан инвариантен относительно цронзвольного параллельного переноса системы в пространстве, 9.11. Используя скобки Пуассона, показать, что обобщенный импульс р, является интегралом движения, если гамильтониан Н(ч1..
до р|. р,) инвариантен относительно преобразования Ь-‘»Ч = Ча+бчь 9.12. С помощью скобок Пуассона показать, что кинети- ческий момент системы сохраняется, если ее гамильтониан %ч Р,’ Н =,7 — + У(г„. ги) ннвариантен относительно произволь- ного бесконечно малого поворота системы. 9.13. Используя скобки Пуассона, показать, что при движении частицы в поле Н()г
) сохраняется ее момент импульса.
9.14. Пусть гамильтониан системы явно не зависит от времени. Доказать, что значение функции Р(д(1), р(1)) канонических пере- менных в момент времени 1 выражается через значение Р(д(0), р(0)) в момент времени 1=0 формулой О Р(4(1), Р(1)) = Р(0) +
1з — „, (( ((РН) Н) ° ) Н)о:и, и=1 где д(1), р(1) — удовлетворяют уравнениям движения, а Р(0) =Р(д(0), р(0)). Вычислить с помощью этой формулы х(1) и р(Г) для одномерного гармонического осциллятора, 9.15. Одномерный точечный осциллятор взаимодействует с полем излучения, гамильтониан которого Н = —
— — — Х (р,’+ совф — гамильто- [Гл 9 Уравнения Гамильтона ниан поля излучения; Н,а=ХВар, — энергия взаимодействия, причем В, = а’ вЂ” ‘ (р,А,(г,)) (индексом ч обозначены величины, л / атно относящиеся к определенной моде поля излучения, индексом з обозначены номера атомов), Используя скобки Пуассона, найти изменение энергии й-той моды, обусловленное взаимодействием с молекулой.
$2. Уравнение Гемкпьтеиа — Якоби 9.17. Найти деиствие материальной точки, движущейся в отсутствие поля н проходящей через точки гт=г(11) н г,=г(1а). 9.18. Найти действне одномерного гармоьического осциллятора, проходящего через точки х1 — — х(11), ха=х(1а). 9.19. Найти действие для одномерного осцнллятора с переменной частотой ат(1). 9.20. Найти действие для заряда, движущегося в однородном магнитном поле. 9.21. Найти полный интеграл уравнения Гамильтона — Якоби для точки движения точки. 9.22. Составить уравнения Гамильтона — Якоби для точки, движущейся в однородном гравитационном поле.
Найти полный интеграл этого уравнения, а также траекторию и закон движения точки. 9.23. Найти полный интеграл уравнения Гамильтона — Якоби для тела, движущегося по гладкой наклонной плоскости, составляющей угол а с горизонтом. 924. Найти полный интеграл уравнения Гамильтона — Якоби для математического маятника и закон его движения в квадратуре. 9.25.
Найти полный интеграл уравнения Гамильтона — Якоби для электрона, движущегося в постоянном однородном магнитном поле (в декартовых координатах) Найти также закон движения электрона и его траекторию. 9 26. Найти полный интеграл уравнения Гамильтона — Якоби для заряда, движущегося в постоянном однородном магнитном поле (в цилиндрических координатах). Получить закон движения и траекторию в квадратурах. 9.27, Найти полный интеграл уравнения Гамильтона — Якоби для электрона, движущегося во взаимно-перпендикулярных постоянных и однородных электрическом н магнитном полях.
9.28. Найти полный интеграл уравнения Гамильтона — Якоби для заряда, движущегося в поле волны с вектором-потенциалом А=асозатй Найти закон движения заряда. 9.29. Однородный стержень массы и скользит по гладкой вер- 65 Канонические преооразовании иариационные принципы тнкальной плоскости, вращающейся вокруг вертикальной оси с постоянной угловой скоростью со (7 — главный центральный момент стержня). Найти полный интеграл уравнения Гамильтона— Якоби для стержня. Определить закон движения стержня. 9.30. Исходя из уравнения Гамильтона — Якоби, получить уравнение, выражающее второй закон Ньютона. 5 3. Канонические преобразования.
Интеграпьные вариационные принципы 9 3!. Нанти каноническое преобразование, соответствующее производящей функции Фз(ч, («, 7) =ХЧД,. 9.32. Показать, что производящая функции Фв(д,Р) =Хч71Р определяет тождественное каноническое преобразование. 9 33 Показать, что выражение
,б(7,) является полным диффереппиалом относительно 2з переменных с7, Я, если «старые» и «новые» переменные подчинены каноническому преобразованию 9.34 Найти каноническое преобразование, соответствующее производяьцсй функции Фв(ч)зеузз7) =дчуз+(Ьд — аР)7, где а, Ь вЂ” константы. Записать и новых переменных уравнения Гамильтона 9.35. Найти каноническое преобразование, задаваемое производящей функцией Ф, = — ы (7) дз с(й е7. 2 Записать уравнения движения в переменных с7, Р для осциллятора с переменной частотой.
9.36 Известна функция Гамильтона системы с двумя степенями свободы 2 Нанти козффициенты аь ае производящей функции канонического преобразования Фз п7 ((7
) с(й Яе, при котором гамильтониан приобретает вид У =-,У, + У’З,У»,. Найти собственные частоты и главные координаты системы. 3 зак« (Гл, 9 Уравнения Гамильтона 9.37. Показать, что гамнльтониан является инвариантом при бесконечно малом каноническом преобразовании с производящей функцией о(д, Р) =-
iSopromat.ru
Пример решения задачи на расчет угловой скорости и углового ускорения конуса, который катится по неподвижной горизонтальной плоскости без скольжения, а также, скорости и ускорения нижней и верхней точек его основания.
Задача
Конус с углом при вершине 2α = 60° и радиусом основания r =20 см катится по неподвижной горизонтальной плоскости без скольжения (Рис. 3.6). Скорость центра основания постоянна, νс= 60 см/сек.
Решение
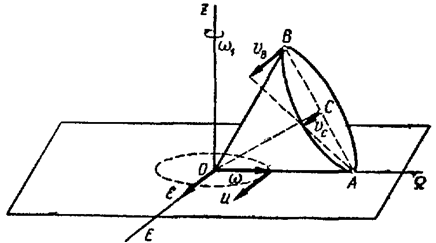
1) рассматриваемое движение конуса является сферическим, так как его вершина остается неподвижной. Так как конус катится по неподвижной плоскости, то образующая OA, которой он соприкасается с плоскостью, является мгновенной осью (все точки этой образующей имеют нулевую скорость).
Зная скорость точки C, можно сразу определить угловую скорость конуса. Найдем расстояние от C до мгновенной оси (рисунок 3.7):
Определяем угловую скорость:
Учитывая направление вектора νс, откладываем вектор ω от точки O вдоль мгновенной оси так, чтобы смотря ему навстречу, видеть вращение конуса происходящим против движения часовой стрелки;
2) для определения углового ускорения ε необходимо построить годограф угловой скорости ω. При качении конуса по горизонтальной плоскости вектор ω перемещается в этой плоскости, поворачиваясь вокруг вертикальной оси z. Так как модуль его не изменяется, то конец вектора ω описывает окружность в горизонтальной плоскости.
Вектор ε геометрически равен скорости u конца вектора ω. В данном случае скорость u является вращательной вокруг оси z. Угловая скорость этого вращения ω1 определяется как угловая скорость вращения оси конуса OC вокруг оси z. Чтобы определить ее модуль, находим расстояние от точки C до оси z:
Скорость u находим как вращательную скорость точки – конца вектора угловой скорости ω при вращении вокруг оси z:
Вектор ε отложен от неподвижной точки в направлении скорости u, т.е. лежит в горизонтальной плоскости и перпендикулярен ω;
3) определим скорости точек A и B. Точка A лежит на мгновенной оси вращения, ее скорость равна нулю νA=0.
Скорость точки B (рисунок 3.7):
Вектор скорости νB направлен перпендикулярно плоскости ΩOz;
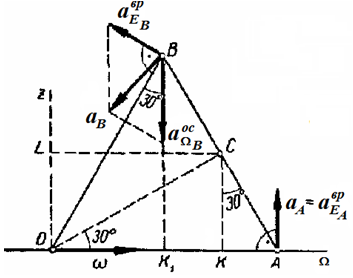
4) точка B имеет ускорение aB, равное сумме осестремительного ускорения aΩB oc и вращательного ускорения aEB вр :
По формулам (3.9) находим:
Для определения модуля aEB вр опустим из B перпендикуляр на ось углового ускорения E. Этот перпендикуляр совпадает с отрезком BO (рисунок 3.6).
Определяем модуль aB как длину диагонали параллелограмма:
В точке A, лежащей на мгновенной оси вращения, осестремительное ускорение равно нулю: aΩA oc =0. Определяем модуль вращательного ускорения точки A (рисунок 3.7):
Вектор aEA вр направлен перпендикулярно AO в плоскости ΩOz.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Порядок выполнения задания
Задача сформулирована отдельно для каждого варианта, чертежи к задачам помещены на схемах, необходимые данные –
в таблице «Исходные данные», с. 33-36 (кроме вариантов, отмеченных звездочкой, с №№ 14, 15, 18, 19, 20, которые содержат исходные данные в условии задачи). Во всех вариантах рассматривается регулярная прецессия твердого тела.
1. Найти неподвижную точку вращения тела, выбираемую за начало отсчета неподвижной (инерциальной) и связанной коорди-натных систем. Выбрать оси прецессии 
, ротации 
.
2. Определить угловые скорости нутации, прецессии, ротации, мгновенную угловую скорость 
и мгновенную ось вращения 
. В зависимости от движения твёрдого тела вектор можно найти двумя путями: 1) определением по ее составляющим (2.1);
2) использованием мгновенной оси вращения.
По известной скорости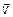 
какой-либо точки М твердого тела и положению оси 
найти величину 
, где 
— кратчайшее расстояние от точки М до мгновенной оси .
3. Определить угловое ускорение 
твердого тела. Как известно, 
, где точка k – конец вектора . В случае регулярной прецессии является закрепленным в точке О векто-ром и определяется по формуле (2.2).
4. Определить скорости произвольных точек твёрдого тела по формуле (2.3).
Так как 
всегда направлено по к оси , можно не пользоваться векторной формой для . Наоборот, 
следует находить только в векторной форме.
Поскольку при вращении около полюса (в отличие от вращения около неподвижной оси) не коллинеарен , то и , вообще говоря, не являются перпендикулярными векторами. Поэтому 
следует находить после построения векторов на чертеже, и величина ускорения будет определяться по (2.6).
Для точек, лежащих на оси ротации твёрдого тела, справедливы и следующие зависимости:
и 
,
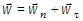
где 
— нормальное ускорение; 
— касательное ускорение; при регулярной прецессии 
; 
— кратчайшее расстояние от точки, лежащей на оси ротации, до оси прецессии 
.
Задание выполняется с приведением эскизных чертежей. Величины, приводимые в таблицах «Исходные данные», считаются точными. Все векторы, лежащие в плоскости xOy (плоскости чертежа), должны быть изображены в этой плоскости; направление других векторов должно быть указано в тексте.
Варианты заданий (условия задач)
Вариант 1.
Прямой круговой конус с углом 2α при вершине катится по плоскости без скольжения таким образом, что ускорение точки С – центра основания конуса – направлено по нормали к ее траектории и равно постоянной величине 
. Высота конуса 
.
1) алгебраические величины проекций угловых скоростей прецессии, ротации и мгновенной угловой скорости на оси 
, 
, 
соответственно;
2) угловое ускорение конуса;
4) ускорения точек А и В (чему равен 
, составленный векторами 
).
Вариант 2.
Прямой круговой усеченный конус катится без скольжения по неподвижной горизонтальной плоскости. Высота конуса 
, радиусы большого и малого оснований равны R и r.
Движение конуса происходит так, что скорость центра большего основания постоянна и равна 
.
1) алгебраические величины проекций угловых скоростей прецессии, ротации и мгновенной угловой скорости на оси , , соответственно;
2) алгебраическую величину проекции углового ускорения на ось 
;
3) скорости точек А и В;
4) ускорения точек В и С.
Вариант 3.
Прямой круговой конус с углом 2α при вершине катится без скольжения по неподвижной плоскости, делая n оборотов в минуту около вертикальной оси . Высота конуса .
1) алгебраические величины проекций угловых скоростей прецессии и ротации на оси и соответственно, а также мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорости точек В и С;
4) ускорение точки В, а также осестремительное и вращатель-ное, нормальное и касательное ускорения точки С.
Вариант 4.
Конус 1 с углом 2α при вершине катится без скольжения
по неподвижному конусу 2 с углом 2β при вершине. Высота конуса 
. Движение конуса происходит так, что осестремительное ускорение центра С основания конуса 
постоянно и равно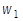 
.
1) алгебраические величины проекций угловых скоростей прецессии и ротации на оси и , соответственно, и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорость точки В;
4) ускорения точек В и С (найти вращательное, а также нормальное и касательное ускорения точки С).
Вариант 5.
Конус 1 с углом 2α при вершине катится без скольжения по неподвижному конусу 2 с углом 2β при вершине так, что скорость точки С центра основания конуса постоянна и равна , 
в данный момент времени. Высота конуса .
1) угловую скорость прецессии, нутации и ротации и мгновенную угловую скорость конуса 1;
2) угловое ускорение конуса;
3) скорости точек А и В;
4) ускорения точек А и С (найти нормальное и осестреми-тельное ускорения точки С).
Вариант 6.
Прямой круговой конус 1 с углом 2α при вершине катится без скольжения по неподвижному конусу 2, обегая его n раз в минуту. Угол при вершине неподвижного конуса равен 2β, радиус основания конуса 1 равен R.
1) угловые скорости прецессии, нутации, ротации и мгновенную угловую скорость конуса 1;
2) алгебраическую величину проекции углового ускорения конуса на ось 
в данный момент времени;
3) скорости точек В и С;
4) ускорение точки С – центра основания конуса. Указать нормальную и касательную составляющие, а также вращательное и осестремительное ускорения точки С. Какой угол γ составляют между собой 
и 
?
Вариант 7.
Конус 1 с углом 2α при вершине катится без скольжения по неподвижному конусу 2 с углом 2β при вершине, совершая за время Т один оборот вокруг вертикальной оси 
против часовой стрелки. Высота конуса .
1) алгебраические величины проекций угловых скоростей прецессии и ротации на оси и 
соответственно и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорость точки В;
4) полное ускорение точки А; вращательное и осестремительное ускорения точки С; какой угол составляют между собой эти векторы?
Вариант 8.
Прямой круговой конус 1 высотой с углом при вершине 2α равномерно катится без скольжения по неподвижному конусу 2 с углом при вершине 2β. Вращательное ускорение центра основания конуса 
.
1) угловое ускорение конуса;
2) угловые скорости прецессии и ротации и мгновенную угловую скорость конуса;
3) скорости точек В и С;
4) осестремительное и полное ускорение точки С, а также касательную и нормальную составляющие ускорения этой точки.
Вариант 9.
Прямой круговой конус 1 высотой с углом при вершине 2α равномерно катится без скольжения по неподвижному конусу 2 с углом при вершине 2β. Ускорение точки М конуса, лежащей на середине его образующей, равно: 
.
1) угловое ускорение конуса;
2) угловые скорости прецессии, ротации и мгновенную угловую скорость конуса;
3) скорости точек С и В;
4) ускорение точки С и точки N, лежащей на середине обра-зующей ОВ.
Вариант 10.
Прямой круговой конус 1 с углом при вершине 2α и радиусом основания R перекатывается без скольжения по неподвижному конусу 2 с углом при вершине 2β. Подвижный конус совершает n оборотов в минуту вокруг своей оси симметрии .
1) угловые скорости прецессии, нутации и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорости точек В и С;
4) вращательное, осестремительное и полное ускорения точки С, а также ее касательное и нормальное ускорения; ускорение точки А.
Вариант 11.
Прямой круговой конус 1 с углом при вершине 2α и радиусом основания R перекатывается без скольжения по неподвижному конусу 2 с углом при вершине 2β. Центр основания конуса С описывает полную окружность 90/π раз в минуту.
Для данного положения конуса (сечение OAB совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угловые скорости прецессии, ротации и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорости точек A и B;
4) ускорение точки С (указать нормальную и касательную составляющие, а также вращательное и осестремительное ускорения точки С). Определить угол γ, который составляют между собой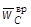 
и 
.
Вариант 12.
Прямой круговой конус 1 высотой с углом 2α при вершине равномерно катится без скольжения по внутренней поверхности конуса 2 с углом 2β при вершине. Ускорение точки М, лежащей на половине образующей ОА, равно: 
.
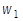
1) Угловые скорости прецессии, нутации, ротации и мгновенную угловую скорость конуса;
2) Угловое ускорение конуса;
4) Ускорения точек В и С.
Вариант 13.
Прямой круговой конус 1 с углом 2α при вершине и радиусом основания R катится без скольжения по внутренней поверхности неподвижного конуса 2 с углом 2β при вершине. Скорость точки С основания конуса постоянна и равна ; 
в данный момент времени.
1) алгебраические величины проекций угловых скоростей прецессии и ротации на оси 
и 
соответственно и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорость точки В;
4) ускорение точки А;
5) ускорение точки N, лежащей на середине образующей ОВ конуса. Под каким углом γ к образующей конуса ОВ направлен вектор 
?
Вариант 14.
Конический каток равномерно вращается вокруг полюса О так, что точка С описывает окружность со скоростью = 2 м/с. Размеры катка: ОС=СА=СВ = 2 м, СK=KM=KN = 1 м.
Для данного положения катка (сечение MABN совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угол нутации, угловые скорости прецессии, ротации и мгновенную угловую скорость катка;
2) угловое ускорение катка;
3) скорости точек A и B;
4) ускорение точек N и C (найти также вращательную и осестремительную, нормальную и касательную составляющие ускорения точки С).
Вариант 15.
Конический каток равномерно вращается вокруг полюса О так, что точка C описывает окружность за π с. Размеры катка: OC=CA=CB = 2 м, CK=KM=KN = 1 м.
Для данного положения катка (сечение MABN совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угловые скорости прецессии, ротации и мгновенную угловую скорость катка.
2) угловое ускорение катка.
3) скорости точек В и N.
4) ускорения точек M и C (найти также вращательную и нормальную составляющие ускорения точки С).
Вариант 16.
Коническая зубчатая шестерня радиуса r, находясь в зацеплении с плоской неподвижной шестерней радиуса R, движется таким образом, что величина ускорения центра С шестерни постоянна и равна 
.
1) угловые скорости прецессии, ротации, нутации и мгновенную угловую скорость шестерни;
2) угловое ускорение шестерни;
4) ускорения точек А и В.
Вариант 17.
Кривошип ОС равномерно вращается против часовой стрелки около вертикальной оси , делая n оборотов в минуту. В точке С на него свободно насажена коническая шестерня радиуса r, перекатывающаяся по зубчатому основанию радиуса R.
Пренебрегая высотой зубьев, определить:
1) алгебраические величины проекций угловых скоростей прецессии, ротации и мгновенной угловой скорости шестерни на оси , и 
соответственно;
2) угловое ускорение шестерни;
3) скорости точек А и В;
4) ускорения точек С и В.
Вариант 18.
Конический каток равномерно вращается вокруг полюса О, имея скорость в центре основания конуса в точке С 
= 2 м/с. Размеры конуса: ОС=СА=СВ = 2 м, СK=KM=KN = 1 м.
Для данного положения катка (сечение MABN совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угловые скорости прецессии, ротации и мгновенную угловую скорость катка;
2) угловое ускорение катка;
3) скорости точек B и K;
4) ускорение точек M и С.
Вариант 19.
Конический каток равномерно вращается вокруг полюса О так, что точка C описывает окружность за π с. Размеры катка: OC=CA=CB = 2 м, CK=KM=KN = 1 м.
Для данного положения катка (сечение MABN совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угловые скорости прецессии, ротации и мгновенную угловую скорость катка;
2) угловое ускорение катка;
3) скорости точек N и B;
4) ускорения точек B и C (указать величины составляющих ускорений точки С: 
, 
).
Вариант 20.
Конический каток равномерно вращается вокруг полюса О, имея скорость в центре С основания конуса = 2 м/с. Размеры конуса: OC=CA=CB = 2 м, CK=KM=KN = 1 м.
Для данного положения катка (сечение MABN совпадает с плоскостью Oxy) и указанного стрелкой направления его движения определить и построить на чертеже:
1) угловые скорости прецессии, ротации, нутации и мгновенную угловую скорость катка;
2) угловое ускорение катка;
3) скорости точек N и C;
4) ускорения точек B и C.
Исходные данные
| № вар | 2α | 2β | h | r | R | vС | w1 | n | T |
| град | м | м/с | м/с 2 | об/мин | с | ||||
| — | 0,12 | — | — | — | 0,  | — | — | ||
| — | 0,12 | — | — | — | 0,  | — | — | ||
| — | 0,10 | — | — | — | 0,  | — | — |
| № вар. | 2α | 2β | h | r | R | vC | w1 | n | T |
| град | м | м/с | м/с 2 | об/мин | с | ||||
| — | — | 0,40 | 0,40 | 0,80 | 2,00 | — | — | — | |
| — | — | 0,  | 0,30 | 0,50 |  | — | — | — | |
| — | — | 0,50 | 0,50 | 1,00 | 1,00 | — | — | — | |
| — | 0,20 | — | — | — | — | — | |||
| — | 0,40 | — | — | — | — | — | |||
| — | 0,30 | — | — | — | — | — | |||
| 0,18 | — | — | — | 0,36 | — | — | |||
| 0,16 | — | — | — | 0,32 | — | — | |||
| 0,15 | — | — | — | 0,30 | — | — | |||
| 0,10 | — | — | 0,20 | — | — | — | |||
| 0.15 | — | — | 0,45 | — | — | — | |||
| 0,20 | — | — | 0,80 | — | — | — | |||
| — | — | 0,30 | — | — | 30/π | — | |||
| — | — | 0,25 | — | — | 60/π | — | |||
| — | — | 0,20 | — | — | 90/π | — | |||
| 0,20 | — | — | — | — | — | ||||
| 0,30 | — | — | — | — | — | ||||
| 0,40 | — | — | — | — | — |
| № вар. | 2α | 2β | h | r | R | VC | w1 | n | T |
| град | м | м/с | м/с 2 | об/мин | с | ||||
| 0,12 | — | — | — | 0,  | — | — | |||
| 0,16 | — | — | — | 0,  | — | — | |||
| 0,20 | — | — | — | 0,  | — | — | |||
| 0,12 | — | — | — | 0,48 | — | — | |||
| 0,16 | — | — | — | 0,72 | — | — | |||
| 0,20 | — | — | — | 0,80 | — | — | |||
| — | — | 0,18 | — | — | — | ||||
| — | — | 0,24 | — | — | — | ||||
| — | — | 0,30 | — | — | — | ||||
| — | — | 0,10 | 0,30 | — | — | — | |||
| — | — | 0,12 | 0,36 | — | — | — | |||
| — | — | 0,14 | 0,42 | — | — | — | |||
| 0,12 | — | — | — | 0,24 | — | — | |||
| 0,15 | — | — | — | 0,30 | — | — | |||
| 0,18 | 0,36 | — | |||||||
| — | — | 0,12 | 0,  | — | — | — | |||
| — | — | 0,15 | 0,  | — | — | — | |||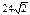
| — | — | 0,18 | 0,  | — | — | — | |||
| 14* | — | ||||||||
| — | — | ||||||||
| — | — | ||||||||
| 15* | — | — | |||||||
| — | |||||||||
| — | — | — | — |
| № вар. | 2α | 2β | h | r | R | vC | w1 | n | T |
| град | м | м/с | м/с 2 | об/мин | с | ||||
| 0,20 | 0,40 | — | 0,90 | — | — | ||||
| — | — | — | 0,30 | 0,60 | — | 1,20 | — | — | |
| — | — | — | 0,20 | 0,  | — | 0,60 | — | — | |
| — | — | — | 0,10 | 0,  | — | — | — | ||
| — | — | — | 0,15 | 0,  | — | — | — | ||
| — | — | — | 0,20 | 0,  | — | — | — | ||
| 18* | |||||||||
| 19* | |||||||||
| 20* |
Рисунки к вариантам 1-20
1) алгебраические величины проекций угловых скоростей прецессии и ротации на оси 
, и 
соответственно и мгновенную угловую скорость конуса;
2) угловое ускорение конуса;
3) скорость точки В;
4) ускорение точек В и С (найти вращательное, а также нормальное и касательное ускорения точки С).
Рис. 2.6
Тогда можно определить
, 
.
Стрелка на pис. 2.6 указывает, что вращение конуса 1 происходит по ходу часовой стрелки, если смотреть с положительного конца оси прецессии 
, поэтому 
противоположна по направлению оси .
2. Далее по теореме синусов для векторного треугольника OMP (см. рис. 2.6) можно записать:
. (2.7)
Векторный треугольник построен так, что 
(оси прецессии), а 
(оси ротации), 
(мгновенной оси вращения).
,
.
Определили угловые скорости прецессии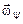 
и ротации 
, соответственно, причем 
.
(2.8)
Имеем регулярную прецессию, так как выполняется условие (2.8).
3. При регулярной прецессии вектор углового ускорения конуса определяется по формуле (2.3) 
.
Величину углового ускорения конуса определить по формуле
,
(см. рис. 2.6).
Вектор углового ускорения 
; в силу (2.2) 
4. Вектор скорости точки В определяется по формуле (2.3): 
.
Тогда величина вектора скорости 
, где 
— кратчайшее расстояние от точки В до мгновенной оси вращения 
.
Вектор скорости точки В по направлению совпадает с осью 
(см. формулу (2.3)).
Вектор вращательного ускорения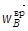 
определить из
векторного произведения (2.5) 
, тогда 
(м/с 2 ).
Вектор 
и направлен в силу (2.5), как показано на рис. 2.6.
Полное ускорение точки В, вектор 
определить по теореме косинусов (2.6): 
. Угол 
=60°, cos60°=0,5.
Тогда 
(м/с 2 ) (с точностью до трех значащих цифр).
Направление вектора 
(см. рис. 2.6) построить как диагональ параллелограмма со сторонами 
. Обратить внимание на то, что угол между не равен 90°, как это бывает при вращении тела вокруг неподвижной оси.
6. Точка 
, поэтому вектор ускорения 
можно определить как векторную сумму касательного 
и нормального 
ускорений точки С, т.е. 
.
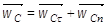
Касательное ускорение 
м/с 2 = const, 
, расстояние от точки С до оси 
, 
.
Вектор 
, направлен к центру О окружности радиуса 
, по которой движется точка С в результате прецессии.
Вращательное ускорение точки С определить по формуле (2.5) векторного произведения 
.
Величина 
(м/с 2 ), 
= 
м.