Унарной позиционной и непозиционной системах счисления чем они отличаются привести примеры
Разница между позиционной и непозиционной системой счисления
Системы счисления классифицируются на 2 основные разновидности — позиционные и непозиционные. В чем заключается специфика тех и других?
Что представляет собой позиционная система счисления?
Рассматриваемая система счисления характеризуется тем, что цифры в ней в зависимости от своей позиции относительно начала числа (при его прочтении слева направо) будут иметь разную силу. Чем правее расположена цифра — тем она слабее. Например, в числе 143 самая сильная цифра — 1, поскольку обозначает сотню, далее по силе — 4, поскольку она обозначает десяток, третья по силе цифра — 3, так как она соответствует единичному числу.
Систем счисления, считающихся позиционными, в мире используется довольно много. В числе самых распространенных — двоичная (применяется в программировании), десятичная (более всего распространена в повседневной жизни), восьмеричная и шестнадцатеричная (в основном они применяются в инженерном деле).
Что представляет собой непозиционная система счисления?
Соответствующая система счисления характеризуется тем, что цифры в ней не всегда делятся по силе в зависимости от позиции относительно начала числа. Разность в их силе, в принципе, возможна, но не всегда является правилом.
Например, римское число XX (двадцать) состоит из двух одинаковых по силе цифр X, каждая из которых обозначает десять. В свою очередь, в числе XV (пятнадцать) первая цифра сильнее, поскольку соответствует десятичному основанию, а вторая — единичному числу пять.
Кроме того, в непозиционной системе счисления, в которой используются римские цифры, число, расположенное левее, может быть более слабым. Например, римская цифра IV, то есть 4, состоит из более слабой, расположенной левее I(единицы) и более сильной, расположенной правее V (пять). Цифра 4 образуется, таким образом, посредством вычитания более слабой цифры из более сильной.
Сравнение
Главное отличие позиционной системы счисления от непозиционной заключается в том, что в первой в структуре числа, состоящего более чем из одной цифры, все цифры отличаются по силе (в общем случае сильнее те, что расположены левее). Во второй системе счисления данная закономерность наблюдается только в некоторых случаях. Вполне возможно, что в структуре числа будут присутствовать цифры с одинаковой силой. При этом если сила цифр разная, необязательно, что более сильные будут располагаться левее, может наблюдаться и обратная ситуация.
Определив,в чем разница между позиционной и непозиционной системой счисления, зафиксируем выводы в таблице.
Позиционные и непозиционные системы счисления



Системы счисления принято делить на два класса: непозиционные и позиционные.
В непозиционных СС от положения (позиции) цифры в записи не зависит величина, которую она обозначает. Характерным примером такой системы счисления является римская СС.
Например, в римской СС число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно двумстам тридцати двум.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются.
Например:
VI = 5 + 1 = 6, а IV = 5 – 1 = 4.
MCMXCVIII = 1000 + (-100 + 1000) + (-10 + 100) + 5 + 1 + 1 + 1 = 1998.
Такие системы счисления используются редко, т.к. не приспособлены для вычислений.
На практике наибольшее распространение получили позиционные системы счисления.
Позиционная система счисления – система счисления, в которой значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр. В каждой позиционной системе счисления имеется основание. Любое число записывается в виде последовательности из цифр основания. Количество цифр основания равно самому основанию. Основание показывает, во сколько раз вес каждой цифры меньше веса цифры, стоящей в старшем соседнем разряде.
Некоторые позиционные системы счисления
| Основание | Система счисления | Знаки |
| Двоичная | 0,1 | |
| Троичная | 0,1,2 | |
| Четвертичная | 0,1,2,3 | |
| Пятиричная | 0,1,2,3,4 | |
| Восьмиричная | 0,1,2,3,4,5,6,7 | |
| Десятиричная | 0,1,2,3,4,5,6,7,8,9 | |
| Двенадцатиричная | 0,1,2,3,4,5,6,7,8,9,А,В | |
| Шестнадцатиричная | 0,1,2,3,4,5,6,7,8,9,А,В,D,E,F |
Числа, которыми мы привыкли пользоваться, называются десятичными и арифметика, которой мы пользуемся, также называется десятичной. Называются они так потому, что каждое число можно составить из набора цифр содержащего 10 символов (цифр) –0123456789.
Возьмём, к примеру, число 246. Его запись означает, что в числе две сотни, четыре десятка и шесть единиц. Следовательно, можно записать следующее равенство:
246 = 200 + 40 + 6 = 2 * 10 2 + 4 * 10 1 + 6 * 10 0
В нашем числе три цифры. Старшая цифра «2» имеет номер 3. Так вот она умножается на 10 во второй степени. Следующая цифра «4» имеет порядковый номер 2 и умножается на 10 в первой степени. Уже видно, что цифры умножаются на десять в степени на единицу меньше порядкового номера цифры.
При этом пользуются следующим алгоритмом:
1) цифра в каждой позиции умножается на основание в степени на 1 меньшую, чем номер позиции;
2) полученные таким образом значения складываются.
12310 = 1 * 10 2 + 2 * 10 1 + 3 * 10 0 ;
В других системам счисления такой перевод будет выглядеть следующим образом:
1238 = 1х8 2 + 2 х 8 1 + 3 х 8 0 = 8310;
1012 = 1 х 2 2 + 0 х 2 1 + 1 х 2 0 = 510;
1Е316 = 1 х 16 2 + 14 х 16 1 + 3 х 16 0 = 48310.
Здесь индекс числа служит указанием на основание системы счисления. Назовем основанием системы счисления число, равное мощности множества (т.е. количеству элементов множества) различных символов, допустимых в каждой позиции числа.
Десятичная система счисления является однородной. Это означает, что одних и тех же символов достаточно для изображения любого числа. Но в повседневной жизни мы пользуемся и неоднородными системами счисления, и системами счисления с другим основанием. Пример тому – неметрические системы единиц (1 пуд=40 фунтов), система счета времени (1 минута = 60 секунд).
В дальнейшем мы будем рассматривать однородные позиционные системы счисления.
Обозначим через p основание системы счисления. Тогда веса позиций числа могут быть представлены следующим образом:
Таким образом, любое число X в позиционной системе счисления с основанием p можно представить в следующей развернутой форме записи:
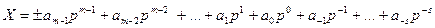
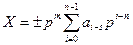
p – основание системы счисления;
m – количество позиций или разрядов, отведенное для изображения целой части числа;
s – количество разрядов, отведенное для изображения дробной части числа;
n = m + s – общее количество разрядов в числе,
ai – любой допустимый символ в разряде (т.е. должен принадлежать множеству <0,1, p-1>).
Заметим, что число, равное основанию системы счисления, в самой системе счисления записывается в виде:
В компьютерных науках наибольшее распространение получила не десятичная, а системы счисления с основанием, кратным 2 – двоичная, восьмеричная, шестнадцатеричная.
В двоичной системе счисления допустимыми символами являются только 0 и 1, а само число может быть представлено в виде последовательности нулей и единиц.
110100102 = 1 * 2 7 + 1 * 2 6 + 0 * 2 5 + 1 * 2 4 + 0 * 2 3 + 0 * 2 2 + 1 * 2 1 + 0 * 2 0 = 16210
В восьмеричной системе счисления допустимыми символами являются 0,1,…7.
2428 = 2 * 8 2 + 4 * 8 1 + 2 * 8 0 = 16210
В шестнадцатеричной системе допустимыми символами являются 0, 1, 9, A, B, C, D, E, F.
A216 = 10 * 16 1 + 2 * 16 0 = 16210
Позиционные и непозиционные системы счисления
Системой счисления называется совокупность приемов и правил представления чисел с помощью цифровых знаков.
Непозиционной называется такая система счисления, в которой значение любой цифры не зависит от положения (позиции) в ряду цифр, изображающих это число.
Например, в числе ХХХ, записанном в римской системе счисления, каждый разряд означает 10 единиц.
Задача 1. Записать числа в римской нумерации: а) 193; б) 564; в) 2708.
Позиционной называется такая система счисления, в которой значение любой цифры зависит от ее положения (позиции) в ряду цифр, изображающих это число.
Например, цифра 3 в числе 723, записанном в десятичной системе счисления, означает три единицы, а в числе 325 – три сотни. К позиционным СС можно отнести шестидесятиричную вавилонскую и десятичную системы счисления.
Под основанием системы счисления понимается определенное постоянное для данной системы счисления отношение единиц соседних разрядов.
Основанием системы счисления может быть любое натуральное число большее 1.
Система счисления с основанием равным 1 называется унарной.
Для записи чисел в позиционной системе счисления используются цифры, количество которых соответствует основанию системы.
Десятичная система счисления, запись чисел в ней
В практике установилась десятичная система счисления. Как известно, в десятичной СС для записи чисел используются 10 знаков (цифр): 1,2,3,4,5,6,7,8,9,0. Из них образуются конечные последовательности, которые являются краткими записями чисел. Например, последовательность 3745 является краткой записью числа 
Определение 4.Десятичной записью натурального числа xназывается его представление в виде:

где коэффициенты an, an-1, …, a1, a0 принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и
Сумму 

Так как понятие числа и его записи нетождественны, то существование и единственность десятичной записи натуральной записи надо доказывать.
Теорема 1. Любое натуральное число х можно представить в виде:

где коэффициенты an, an-1, …, a1, a0 принимают значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
и такая запись единственная.
Десятичная запись числа позволяет просто решать вопрос о том, какое из них меньше.
Теорема 2. Пусть х и у – натуральные числа, запись которых дана в десятичной системе счисления:

Тогда число х меньше числа у, если выполнено одно из условий:
Три первых разряда в записи числа соединяют одну группу и называют первым классом, или классом единиц. В первый класс входят единицы, десятки и сотни.
Четвертый, пятый и шестой разряды в записи числа образуют второй класс – класс тысяч. Затем следует третий класс – класс миллионов, состоящий тоже из трех разрядов: седьмого, восьмого и девятого, т.е. из единиц миллионов, десятков миллионов и сотен миллионов.
Последующие три разряда также образуют новый класс и т.д. выделение классов единиц, тысяч, миллионов и т.д. создает удобства для записи и прочтения чисел.
В десятичной СС всем числам можно дать название (имя). это достигается следующим образом: имеются названия первых 10 чисел, затем из них в соответствии с определением десятичной записи и путем прибавления еще немногих слов образуются названия последующих чисел. Так числа второго десятка, представляемые в виде 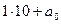
Может быть естественнее было бы говорить «два и десять», но наши предки предпочли говорить «два на десять», что и сохранилось в речи.
Таким образом, чтобы назвать все натуральные числа в пределах миллиарда, потребовалось только 16 различных слов: один, два, три, четыре, пять, шесть, семь, восемь, девять, десять, сорок, девяносто, сто, тысяча, миллион, миллиард. Остальные названия чисел (в пределах миллиарда) образуются из основных.
Определение позиционной и непозиционной системы счисления
Системы счисления
Система счисления — метод записи чисел с помощью письменных знаков.
Системы делятся на позиционные, непозиционные и смешанные. Смысл их в том, чтобы дать каждому числу уникальное представление. В разных системах одно и то же число может быть записано по-разному. Символы, используемые для записи чисел, называют цифрами, даже когда система использует в дополнение к арабским цифрам или вместо них буквы латинского алфавита.
Что такое позиционная система
Позиционная система счисления — система счисления, в которой значение каждого числового знака в записи числа зависит от его позиции.
В позиционной системе количественный эквивалент каждой цифры зависит от места ее записи в коде числа. Любое целое число x в d-ичной позиционной системе счисления является конечной линейной комбинацией степеней числа d:
k — показатель разряда.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В общем случае представить произвольное число x в системе счисления с заданным основанием d означает расписать его по формуле:
Таким образом, в любой позиционной системе число может быть представлено в виде многочлена.
Что такое непозиционная система
Непозиционная система — это такая система счисления, в которой положения цифры в записи числа не зависит величина, которую она обозначает.
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от ее места в коде числа.
Еще до нашей эры разные народы независимо друг от друга отказывались от унарной системы счисления, в которой количество предметов обозначали таким же количеством одинаковых значков, и переходили к более удобным системам. Например, у египтян система счисления была десятичной, но запись числа составлялась только из иероглифов 1, 10, 100, 1000. Их нужно было складывать, поэтому не имело значения, в каком порядке они записаны.
Отличие между системами
Чтобы пользоваться позиционной системой счисления, достаточно знать, как в ней изображаются цифры и что они обозначают, а также ее основание — количество уникальных цифр. Порядок записи во всех позиционных системах одинаков.
В непозиционных системах количество цифр-символов может достигать десятков и даже сотен, так как для записи больших чисел постоянно приходится вводить новые символы. Для чтения числа нужно знать правила его записи. Часто приходится выполнять арифметические операции, например, вычитание и сложение.
Достоинства позиционной системы
Простое выполнение подсчета
У всех позиционных систем одни и те же алгоритмы выполнения арифметических действий. Также в позиционных системах удобно работать с дробями и отрицательными числами, которые зачастую просто невозможно представить в непозиционных системах.
Главные свойства позиционных систем:
Малое количество символов в записи
Позиционные системы используют только десять арабских цифр. Системы с основанием больше десяти добавляют к цифрам 26 латинских букв. В некоторых системах используют круглые и квадратные скобки.
Чем больше основание системы счисления, тем меньшее количество цифр понадобится для записи числа. Числа, состоящие из трех разрядов в десятичной системе, могут иметь всего два разряда в шестнадцатеричной.
Основание позиционной системы
Обычно за основание принимают целое натуральное число. Но существуют также системы с дробным или отрицательным основанием. Последние называют нега-позиционными.
Основание позиционной системы счисления — это количество уникальных символов, изображающих ее цифры.
Таким образом, чтобы найти эту главную характеристику любой позиционной системы, достаточно подсчитать количество цифр в ней.
Классификация позиционных систем
Двоичные
Двоичная система — система счисления, в которой в качестве базовых чисел выбираются степени числа два.
Чтобы не путать их с числами, записанными в десятичной системе счисления, справа внизу указывают основание системы счисления. Обычно число при этом заключают в скобки.
Двоичную систему использовали задолго до возникновения информационных технологий. Во втором тысячелетии до нашей эры народы Южной Америки кодировали двоичной системой свои записи, в том числе и не числовые. Узелок и ровный участок нити чередовались друг с другом.
В современной двоичной системе, на основе которой был создан телеграф, а позже — реле и переключатели, единица обозначает наличие сигнала, ноль — его отсутствие. Цифровые электронные схемы работают по тому же принципу. Также на нем основаны сигнальные системы, использующиеся до сих пор, например, азбука Морзе.
Восьмеричные
Когда-то два индейских племени решили, что им удобно при счете смотреть на восемь промежутков между пальцами, а не на сами пальцы. Восьмеричная система счисления отразилась в их языках, в которых только восемь слов, обозначающих цифры.
В двадцатом веке, когда для написания программ требовалось зашифровывать все больше информации в двоичной системе и упростить вычисления для людей, придумали альтернативную систему, которая позволила сократить количество цифр в коде. Число восемь — это два в кубе, поэтому перевести записи из двоичной системы в восьмеричную и обратно проще, чем в десятичную.
Десятичные
Элементы числовой базы, или ключевые числа, в десятичной системе счисления представляют собой степени десяти: 10 = 10^1, 100 = 10^2, 1000 = 10^3.
В системе всего десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число 10 — основание системы счисления. Цифры от 0 до 9 представляют собой коэффициенты разложения числа по степеням десяти.
Родиной десятичной системы счисления считается Индия, хотя еще в вавилонской цивилизации с ее шестидесятеричной системой использовались закодированные десятичные цифры, а инки в своей узелковой письменности кодировали информацию десятью цветами. Но именно в Индии начали строго соблюдать порядок разрядов числа при записи и ставить ноль, чтобы избежать путаницы. Примерно в середине VIII века эту систему стали использовать другие страны. В Европе она распространилась к XVI веку и была названа «арабской».
Шестнадцатеричные
Шестнадцатеричные системы, как и восьмеричные, появились для упрощения взаимодействия с компьютером. Кроме арабских цифр, в них используются еще и латинские буквы от А до F. В разных языках программирования для записи чисел в шестнадцатеричной системе разные правила, называемые синтаксисом.
Пятеричная
Система, связанная с количеством пальцев на одной руке, использовалась в Китае и у некоторых племен Африки. В китайском языке у иероглифов, обозначающих цифры от шести до девяти, был один и тот же знак в начале — сокращенное обозначение цифры пять. Для записи чисел в этой системе используются цифры 0, 1, 2, 3, 4.
Двенадцатеричная
Если большим пальцем руки сосчитать число фаланг на других пальцах этой руки, получится двенадцать. Группы по двенадцать предметов называли во многих европейских языках словами, схожими с русским словом «дюжина»: duodezim на латыни, douzaine на французском, dozzina на итальянском, dozen на английском. Римляне пользовались двенадцатеричными дробями, \frac1 <12>они называли унцией.
В Европе счет дюжинами долгое время, вплоть до XVIII века, сохранялся наравне с десятеричной системой. Дюжина дюжин составляла гросс (от немецкого слова «большой»), дюжина гроссов — массу. Признаки влияния числа 12 заметны в англо-американской системе линейных мер, в которой 1 фут равен 12 дюймам, 1 дюйм — 12 линиям, 1 линия — 6 точкам.
Шестидесятеричная
Первой позиционной системой счисления считается шестидесятеричная система в Древнем Вавилоне. Ее основание до сих пор применяют для измерения времени. Система счисления времени — смешанная, но для перевода минут в секунды или часы потребуется именно шестидесятеричная система.
Для измерения углов и записи координат (широты, долготы) тоже используют эту систему, так как изначально астрономические координаты записывали в шестидесятеричных дробях. По аналогии с часом градус делят на шестьдесят минут, минуту — на шестьдесят секунд.
Двадцатеричная
Двадцатеричную систему называют вигезимальной. Эта система, как и десятеричная, связана с количеством пальцев, поэтому многие народы изобрели ее независимо друг от друга. Основание 20 сохранилось в лингвистической структуре их языков, именно на нем основана система счета в разговорной речи. Например, во французском языке «восемьдесят» состоит из слов «четыре» и «двадцать».
Римская система счисления
Описание
Римская система счисления относится к непозиционным. Она известна всему миру и широко применяется до сих пор. Это связано не с какими-то особыми достоинствами, а скорее с политическим и культурным влиянием Древнего Рима на европейскую цивилизацию.
Сейчас римская система используется в русском языке для обозначения:
В других странах свои особенности употребления римских цифр: в Европе ими часто записывают номер года, в Латвии — день недели.
Считается, что в основу римских цифр легли жесты:
100 и 1000 обозначаются буквами C и М — первыми буквами соответствующих латинских слов.
Основные характеристики
Для записи чисел используют семь букв латинского алфавита:
Сначала записываются тысячи, потом сотни, потом десятки и единицы. Ноль в системе отсутствует, но раньше вместо него использовали букву N. От позиционных систем римская отличается использованием принципов сложения и вычитания. Когда большая цифра стоит перед меньшей, они складываются. Когда меньшая стоит перед большей — вычитаются.