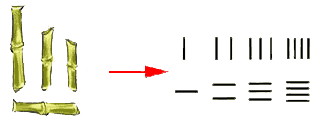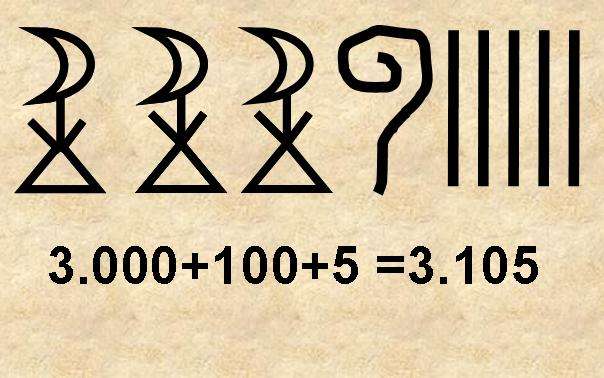Унарная система что это
Унарная система счисления
Здравствуйте, в этой статье пойдет речь про унарную систему счисления. Ниже мы разберем основные определения, касающиеся данной темы, историю происхождения, её достоинства и недостатки. Рассмотрим области, где применяется эта система исчисления, примеры и её значение в информатике и других прикладных науках.
Экскурс в прошлое
Как только древние люди научились подсчитывать предметы, то сразу появилась потребность в отображении чисел. Для подсчета добычи, овец или жителей племени использовались зарубки на деревьях, засечки на костях животных и стенах пещер, камушки, и другие предметы, с помощью которых можно отобразить количественное значение.
Пример У.С: засечки на кости
Ученые археологи нашли такие «записи», которые сохранились до наших дней со времен Палеолита. А это, немного немало, около десяти тысяч лет до нашей эры. Со временем люди стали объединять предметы в группы, появились более совершенные позиционные системы. Однако единичная система исчисления, еще называемая учеными унарной, никуда не ушла – человечество пользуется ей до сих пор. Рассмотрим её более подробно…
Определение и его разъяснение
Унарной – называется непозиционная система счисления, которая состоит всего лишь из одного знака (цифры), который обозначает единицу. Как было написано выше, за «знак» можно было взять всё что угодно – палочку на стене пещеры или зарубку на дереве.
Теперь немного поговорим, почему она называется непозиционной. Тут все очень просто – в таких отображениях положение знака (цифры) не влияет на его значение. Возьмите две спички и примите одну за единицу, поменяйте их местами – число не изменится, каждая спичка, как обозначала 1, так и будет её обозначать.
В позиционных исчислениях все несколько иначе. Давайте возьмем в пример, самое популярное в мире, десятичное счисление. Запишите число 10 и поменяйте нулик с единичкой местами – у вас получится другое число (01). Почему так вышло? Дело в том, что в первом случае 1 обозначала количество десятков, а во втором количество единиц. То есть, поменяв место цифры, мы изменили её значение. Поэтому представление называется позиционным. Далее рассмотрим несколько интересных фактов.
Интересные исторические факты
Не одна древняя цивилизация не использовала примитивную унарную запись в чистом виде, однако она лежала в основе большинства форм представления чисел существовавших в древности.
Преимущества и недостатки
Скорее всего, Вы сами о них уже догадались. К преимуществам унарной формы можно отнести простоту – используется всего лишь один знак, а это значит, что легко выполняются простейшие математические операции, такие как сложение и вычитание.
Недостатков же больше и они очень существенные. Именно из-за них люди предпочли использовать позиционные нумерации:
Примеры применения в мире, информатике и других науках
Заключение
Вот Вы и познакомились с самой примитивной – непозиционной унарной системой счисления. Теперь Вы знаете основные положения и примеры, касающиеся этой темы, области применения в информатике и других сферах. При возникновении вопросов задавайте их в комментариях. А также можете прочитать про Греческий формат.
Единичная система счисления
Уна́рная систе́ма счисле́ния (единичная система счисления) — не-позиционная (не-поместная), положительная суммарная целочисленная система счисления с основанием равным 1.
Может рассматриваться и как вырожденная позиционная (поместная) положительная целочисленная система счисления с основанием равным 1.
В качестве единственной «цифры» используется зарубка или чёрточка (|).
Особенностью такой системы является то, что если приписать к числу одну «цифру» (единицу), то число увеличивается лишь на эту единицу.
(Для сравнения: если в обычной десятичной системе счисления к натуральному числу приписать справа 1, число увеличивается сразу в 10 раз — и плюс 1).
Поэтому такая система записи чисел обычно применяется там, где идёт последовательное увеличение подсчитываемой величины, например: при счёте числа дней, количества одинаковых событий и т. п.
Вероятно, подобная система является древнейшей системой счисления в истории человечества, для примера можно привести Московский математический папирус, датируемый приблизительно 1850 до н. э.
Содержание
Примеры использования
5: ||||| (иногда 
Применение
См. также
Ссылки
Полезное
Смотреть что такое «Единичная система счисления» в других словарях:
Система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Унарная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Позиционная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Троичная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Двоичная система счисления — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия
Двенадцатеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Кириллическая система счисления — Башенные часы с кириллическими числами в Суздале … Википедия
Вигезимальная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Двадцатеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Шестидесятеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Унарная система счисления
| Системы счисления в культуре | |
|---|---|
| Индо-арабская система счисления | |
| Арабская Индийские Тамильская Бирманская | Кхмерская Лаоская Монгольская Тайская |
| Восточноазиатские системы счисления | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные системы счисления | |
| Абджадия Армянская Ариабхата Кириллическая | Греческая Эфиопская Еврейская Катапаяди |
| Другие системы | |
| Вавилонская Египетская Этруская Римская | Аттическая Кипу Майская |
| Позиционные системы счисления | |
| Десятичная система счисления (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60 | |
| Нега-позиционная система счисления | |
| Симметричная система счисления | |
| Смешанные системы счисления | |
| Фибоначчиева система счисления | |
| Непозиционные системы счисления | |
| Единичная (унарная) система счисления | |
| Список систем счисления | |
Уна́рная (едини́чная, ра́зная) систе́ма счисле́ния — положительная суммарная целочисленная система счисления с основанием, равным 1.
В качестве единственной «цифры» используется «1», чёрточка (|), камешек, костяшка счёт, узелок, зарубка и др. [1]
Попытки записи чисел с целой и дробной частью только одной цифрой в строчку пока безуспешны; однако их можно записывать в столбик.
Содержание
Единичные непозиционные системы счисления
Единичные системы счисления с весовыми функциями (коэффициентами) f=b, независящими от положения цифр, являются непозиционными (непоместными). Числа в них могут быть записаны в виде:

Поскольку весовой коэффициент b может быть любым, число единичных непозиционных систем счисления бесконечно. Наибольшее распространение получила единичная непозиционная система счисления с весовым коэффициентом, равным единице (b=1). В народе иногда применяется единичная непозиционная система счисления с весовым коэффициентом, равным двум (b=2) — при счёте па́рами.
Из комбинаторики известно, что число записываемых кодов не зависит от основания весового коэффициента — b, который определяет диапазон представляемых числами x1,b величин, и равно числу размещений с повторениями:

a=1 — одноэлементное множество a= из которого берутся цифры ak, :n — число элементов (цифр) в числе x1,b.
Из этого следует, что вышеприведённая запись для фиксированного числа разрядов — n определяет одно число. Сумма таких записей с числом разрядов n от 1 до n определяет n единичных чисел.
Единичная непозиционная система счисления с единичным весовым коэффициентом
Целые числа записываются в виде:

Особенностью такой системы является то, что если приписать к числу одну «цифру» (1 — единицу), то число увеличивается лишь на эту единицу.
(Для сравнения: если в обычной десятичной системе счисления к натуральному числу приписать справа 1, число увеличивается сразу в 10 раз — и плюс 1).
Поэтому такая система записи чисел обычно применяется там, где идёт последовательное увеличение подсчитываемой величины, например: при счёте числа дней, количества одинаковых событий и т. п.
Вероятно, подобная система является древнейшей системой счисления в истории человечества, для примера можно привести Московский математический папирус, датируемый приблизительно 1850 до н. э.
Дробные числа записываются в виде дроби из двух целых чисел:

n — число цифр числителя (a1) дробного числа x1, m — число цифр знаменателя (a2) дробного числа x1.
Примеры использования
5: ||||| (иногда 
Применение
Единичнодесятичное (унарнодесятичное) кодирование
Подобно двоично-десятичному кодированию, в обычной десятичной системе счисления внутри каждого разряда возможно единичнодесятичное (унарнодесятичное) кодирование, в котором каждой арабской цифре от «0» до «9» соответствует свой единичный (унарный) код от «» до «111111111».
Единичнодвоичное (унарнодвоичное) кодирование
В обычной двоичной системе счисления, применяемой в вычислительной технике, внутри каждого разряда возможно использование единичнодвоичного (унарнодвоичного) кодирования, в котором каждой арабской цифре от «0» до «1» соответствует свой единичный (унарный) код от «» до «1».
Единичнотроичное (унарнотроичное) кодирование
В обычной троичной системе счисления, применяемой в вычислительной технике, внутри каждого разряда возможно применение единичнотроичного (унарнотроичного) кодирования, в котором каждой арабской цифре от «0» до «2» соответствует свой единичный (унарный) код от «» до «11».
Единичночетверичное (унарночетверичное) кодирование
В обычной четверичной системе счисления, применяемой в вычислительной технике, внутри каждого разряда возможно применение единичночетверичного (унарночетверичного) кодирования, в которой каждой арабской цифре от «0» до «3» соответствует свой единичный (унарный) код от «» до «111».
Единичные позиционные системы счисления
Если весовые коэффициенты 




Пример: при
При 
При межразрядной функции 

в которых множество 



Дробные числа записываются в виде:



См. также
Примечания
Ссылки
Полезное
Смотреть что такое «Унарная система счисления» в других словарях:
Система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Позиционная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Троичная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Комбинированная система счисления — В комбинированных системах счисления для записи чисел используются две или более систем счисления с разными основаниями. В общем случае возможно бесконечное множество комбинированных систем счисления. В спаренных (сдвоенных, двойных) системах… … Википедия
Двоичная система счисления — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия
Двенадцатеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Кириллическая система счисления — Башенные часы с кириллическими числами в Суздале … Википедия
Вигезимальная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Двадцатеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Шестидесятеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Унарная система счисления
Вы будете перенаправлены на Автор24
Унарная система счисления — это непозиционная система счисления, состоящая из одной цифры, которая обозначает единицу.
Введение
Ещё с древности человека стали интересовать числа. Люди подсчитывали число дней в году, количество созвездий в небе, различные финансовые траты на сооружение строений, обустройство дорог и тому подобное. Без всякой натяжки возможно считать, что цифры заложены в основание жизнедеятельности человека практически любого вида. Для выполнения каких-либо математических расчётов, нужно обладать соответствующей системой и научиться её использовать.
Под системой счисления понимается набор символов и законов формирования на их базе числовых значений и осуществления арифметических действий.
Таким образом, применяя систему счисления, возможно производить разные вычислительные процедуры и в финале сформировать итог разрешения сформулированной задачи в форме числового значения. Очень важна в разных системах счисления форма выражения числовых значений. Можно разделить возможные форматы чисел на позиционные и непозиционные.
Для позиционного представления чисел, вес каждой цифры определяется её позицией в числовом выражении. Для непозиционного формата числа положение цифры в общем «списке» символов числа не имеет значения.
Готовые работы на аналогичную тему
Унарная система счисления
Под унарной системой счисления понимается метод отображения числовых значений, основанный на единственном цифровом символе.
Согласно данным историков, неизвестны древние цивилизации, которые бы применяли такую примитивнейшую систему для вычислительных операций, однако подтверждён такой факт, что унарная система счисления была положена в основу почти всех представлений о числах в древние времена. В качестве примера можно взять древний Египет. Там унарную систему применяли, чтобы считать от одного до десяти, а далее прибавляли новое обозначение для десятков и считали дальше, суммируя палочки. Когда счёт достигал сотен, опять применялся новый необходимый знак, и продолжали далее. Римская система тоже в своей основе имела унарную систему. Правильность такого вывода можно подтвердить, взглянув на первые три цифры: I, II, III. Истоки унарных систем счисления можно найти и у цивилизаций востока. Например, чтобы посчитать что-либо древние китайцы, японцы и корейцы по аналогии с римской системой, вначале применяли унарные методы счёта, а впоследствии добавляли новую символику.
Примеры применения унарной системы
Невзирая на очень простую структуру, унарные принципы используются и сегодня при осуществлении определённого класса вычислительных процедур. Обычно, эта система обнаруживает свою простоту и полезность в применении в тех случаях, когда не имеет значения финальное число компонентов, и требуется производить процесс счёта просто путём прибавления или вычитания одного компонента. Можно привести следующие примеры использования унарной системы счисления:
Достоинства и недостатки унарных систем
Основное достоинство мы обозначили немного выше, и оно состоит в применении всего единственного знака («|») для выражения любого числа компонентов. Помимо этого, унарное представление чисел позволяет крайне просто производить арифметические операции. Однако недостатки унарной системы счисления имеют существенно больший вес, чем достоинства. Например, отсутствие ноля становится большой преградой для математических вычислений.
Унарная система счисления: исторические факты и использование в современном мире
С древних времен людей интересовали числа. Они считали количество дней в году, число звезд на небе, объемы собранного зерна, затраты на строительство дорог и зданий и так далее. Без преувеличения можно сказать, что числа лежат в основе человеческой деятельности абсолютно любого характера. Для того чтобы выполнить математический счет, необходимо иметь соответствующую систему и уметь ей пользоваться. В данной статье речь пойдет об унарной системе счисления.
Понятие о системе счисления

Под этим понятием подразумевают совокупность символов, правил составления из них чисел и выполнения математических операций. То есть, используя систему счисления, можно выполнять различные вычисления и получать результат решения поставленной проблемы в виде числа.
Важную роль в различных системах счисления играет способ представления чисел. В общем случае принято выделять позиционное и непозиционное представления. В первом случае значение цифры зависит от позиции, в которой она находится, во втором случае значение цифры в числе не отличается от такового, если бы цифра независимо образовывала число.
Унарная система счисления
Чтобы представить некоторое количество каких-либо элементов N в унарной системе счисления, достаточно подряд написать N соответствующих символов («|»). Например, число 5 запишется таким образом: |||||.
Способы представления числа в унарной системе
Из приведенного выше примера становится очевидным, что если увеличивать число элементов, то необходимо будет для их представления написать много «палочек», что является крайне неудобным. Поэтому люди придумали различные способы упрощения записи и чтения чисел в рассматриваемой системе счисления.
Историческая справка
Ни одна известная древняя цивилизация не применяла эту примитивную систему для выполнения вычислений, однако, точно установлен следующий факт: унарная система счисления лежала в основе практических всех численных представлений в древности. Приведем следующие примеры:
Примеры использования рассматриваемой системы
Несмотря на всю свою простоту, унарная система применяется в настоящее время при выполнении некоторых математических операций. Как правило, она оказывается полезной и простой в использовании для случаев, когда неважно конечное количество элементов, и необходимо счет вести по одному, добавляя или вычитая элемент. Так примерами унарной системы счисления являются следующие:
Преимущества и недостатки унарной системы
Главное преимущество уже было названо, оно заключается в использовании всего одного символа («|») для представления любых количеств элементов. Кроме того, с использованием унарной системы счисления легко выполнять сложение и вычитание.
Недостатки ее применения являются более весомыми, чем преимущества. Так, в ней нет нуля, что является огромным препятствием для развития математики. Большие числа в унарной системе представлять крайне неудобно, а такие операции с ними, как умножение и деление, являются чрезвычайно сложными.
Указанные причины объясняют тот факт, что применяется рассматриваемая система только для малых чисел, и только для простых математических операций.