Укажите что принято за минимальную единицу измерения информации
Информатика. 7 класс
Конспект урока
Единицы измерения информации
Перечень вопросов, рассматриваемых в теме:
Каждый символ информационного сообщения несёт фиксированное количество информации.
Единицей измерения количества информации является бит – это наименьшаяединица.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Формулы, которые используются при решении типовых задач:
Информационный объём сообщения определяется по формуле:
I – объём информации в сообщении;
К – количество символов в сообщении;
i – информационный вес одного символа.
Теоретический материал для самостоятельного изучения.
Любое сообщение несёт некоторое количество информации. Как же его измерить?
Одним из способов измерения информации является алфавитный подход, который говорит о том, что каждый символ любого сообщения имеет определённый информационный вес, то есть несёт фиксированное количество информации.
Сегодня на уроке мы узнаем, чему равен информационный вес одного символа и научимся определять информационный объём сообщения.
Что же такое символ в компьютере? Символом в компьютере является любая буква, цифра, знак препинания, специальный символ и прочее, что можно ввести с помощью клавиатуры. Но компьютер не понимает человеческий язык, он каждый символ кодирует. Вся информация в компьютере представляется в виде нулей и единичек. И вот эти нули и единички называются битом.
Информационный вес символа двоичного алфавита принят за минимальную единицу измерения информации и называется один бит.
Эту формулу можно применять для вычисления информационного веса одного символа любого произвольного алфавита.
Алфавит древнего племени содержит 16 символов. Определите информационный вес одного символа этого алфавита.
Составим краткую запись условия задачи и решим её:
Информационный вес одного символа этого алфавита составляет 4 бита.
Сообщение состоит из множества символов, каждый из которых имеет свой информационный вес. Поэтому, чтобы вычислить объём информации всего сообщения, нужно количество символов, имеющихся в сообщении, умножить на информационный вес одного символа.
Математически это произведение записывается так: I = К · i.
Например: сообщение, записанное буквами 32-символьного алфавита, содержит 180 символов. Какое количество информации оно несёт?
I = 180 · 5 = 900 бит.
Итак, информационный вес всего сообщения равен 900 бит.
В алфавитном подходе не учитывается содержание самого сообщения. Чтобы вычислить объём содержания в сообщении, нужно знать количество символов в сообщении, информационный вес одного символа и мощность алфавита. То есть, чтобы определить информационный вес сообщения: «сегодня хорошая погода», нужно сосчитать количество символов в этом сообщении и умножить это число на восемь.
I = 23 · 8 = 184 бита.
Значит, сообщение весит 184 бита.
Как и в математике, в информатике тоже есть кратные единицы измерения информации. Так, величина равная восьми битам, называется байтом.
Бит и байт – это мелкие единицы измерения. На практике для измерения информационных объёмов используют более крупные единицы: килобайт, мегабайт, гигабайт и другие.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Итак, сегодня мы узнали, что собой представляет алфавитный подход к измерению информации, выяснили, в каких единицах измеряется информация и научились определять информационный вес одного символа и информационный объём сообщения.
Материал для углубленного изучения темы.
Как текстовая информация выглядит в памяти компьютера.
Набирая текст на клавиатуре, мы видим привычные для нас знаки (цифры, буквы и т.д.). В оперативную память компьютера они попадают только в виде двоичного кода. Двоичный код каждого символа, выглядит восьмизначным числом, например 00111111. Теперь возникает вопрос, какой именно восьмизначный двоичный код поставить в соответствие каждому символу?
Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код ‑ просто порядковый номер символа в двоичной системе счисления.
Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.Таблица для кодировки – это «шпаргалка», в которой указаны символы алфавита в соответствии порядковому номеру. Для разных типов компьютеров используются различные таблицы кодировки.
Таблица ASCII (или Аски), стала международным стандартом для персональных компьютеров. Она имеет две части.
В этой таблице латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Это правило соблюдается и в других таблицах кодировки и называется принципом последовательного кодирования алфавитов. Благодаря этому понятие «алфавитный порядок» сохраняется и в машинном представлении символьной информации. Для русского алфавита принцип последовательного кодирования соблюдается не всегда.
Запишем, например, внутреннее представление слова «file». В памяти компьютера оно займет 4 байта со следующим содержанием:
01100110 01101001 01101100 01100101.
А теперь попробуем решить обратную задачу. Какое слово записано следующим двоичным кодом:
01100100 01101001 01110011 01101011?
В таблице 2 приведен один из вариантов второй половины кодовой таблицы АSСII, который называется альтернативной кодировкой. Видно, что в ней для букв русского алфавита соблюдается принцип последовательного кодирования.
Вывод: все тексты вводятся в память компьютера с помощью клавиатуры. На клавишах написаны привычные для нас буквы, цифры, знаки препинания и другие символы. В оперативную память они попадают в форме двоичного кода.
Из памяти же компьютера текст может быть выведен на экран или на печать в символьной форме.
Сейчас используют целых пять систем кодировок русского алфавита (КОИ8-Р, Windows, MS-DOS, Macintosh и ISO). Из-за количества систем кодировок и отсутствия одного стандарта, очень часто возникают недоразумения с переносом русского текста в компьютерный его вид. Поэтому, всегда нужно уточнять, какая система кодирования установлена на компьютере.
Разбор решения заданий тренировочного модуля
№1. Определите информационный вес символа в сообщении, если мощность алфавита равна 32?
№2. Выразите в килобайтах 2 16 байтов.
2 6 = 64, а 2 10 байт – это 1 Кб. Значит, 64 · 1 = 64 Кб.
№3. Тип задания: выделение цветом
8 х = 32 Кб, найдите х.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 1.6. Измерение информации
Информатика. 7 класса. Босова Л.Л. Оглавление
1.6.1. Алфавитный подход к измерению информации
Одно и то же сообщение может нести много информации для одного человека и не нести её совсем для другого человека. При таком подходе количество информации определить однозначно затруднительно.
Алфавитный подход позволяет измерить информационный объём сообщения, представленного на некотором языке (естественном или формальном), независимо от его содержания.
Для количественного выражения любой величины необходима, прежде всего, единица измерения. Измерение осуществляется путём сопоставления измеряемой величины с единицей измерения. Сколько раз единица измерения «укладывается» в измеряемой величине, таков и результат измерения.
При алфавитном подходе считается, что каждый символ некоторого сообщения имеет определённый информационный вес — несёт фиксированное количество информации. Все символы одного алфавита имеют один и тот же вес, зависящий от мощности алфавита. Информационный вес символа двоичного алфавита принят за минимальную единицу измерения информации и называется 1 бит.
Обратите внимание, что название единицы измерения информации «бит» (bit) происходит от английского словосочетания binary digit — «двоичная цифра».
За минимальную единицу измерения информации принят 1 бит. Считается, что таков информационный вес символа двоичного алфавита.
1.6.2. Информационный вес символа произвольного алфавита
Разрядность двоичного кода принято считать информационным весом символа алфавита. Информационный вес символа алфавита выражается в битах.
Задача 1. Алфавит племени Пульти содержит 8 символов. Каков информационный вес символа этого алфавита?
Решение. Составим краткую запись условия задачи.
Полная запись решения в тетради может выглядеть так:
1.6.3. Информационный объём сообщения
Информационный объём сообщения (количество информации в сообщении), представленного символами естественного или формального языка, складывается из информационных весов составляющих его символов.
Информационный объём сообщения I равен произведению количества символов в сообщении К на информационный вес символа алфавита i;I = К • i.
Задача 2. Сообщение, записанное буквами 32-символьного алфавита, содержит 140 символов. Какое количество информации оно несёт?
Задача 3. Информационное сообщение объёмом 720 битов состоит из 180 символов. Какова мощность алфавита, с помощью которого записано это сообщение?
1.6.4. Единицы измерения информации
1 байт = 8 битов
Бит и байт — «мелкие» единицы измерения. На практике для измерения информационных объёмов используются более крупные единицы:
1 килобайт = 1 Кб = 1024 байта = 2 10 байтов
1 мегабайт = 1 Мб = 1024 Кб = 2 10 Кб = 2 20 байтов
1 гигабайт = 1 Гб = 1024 Мб = 2 10 Мб = 2 20 Кб = 2 30 байтов
1 терабайт = 1 Тб = 1024 Гб = 2 10 Гб = 2 20 Мб = 2 30 Кб = 2 40 байтов
Задача 4. Информационное сообщение объёмом 4 Кбайта состоит из 4096 символов. Каков информационный вес символа используемого алфавита? Сколько символов содержит алфавит, с помощью которого записано это сообщение?
Ответ: 8 битов, 256 символов.
Задача 5. В велокроссе участвуют 128 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер цепочкой из нулей и единиц минимальной длины, одинаковой для каждого спортсмена. Каков будет информационный объём сообщения, записанного устройством после того, как промежуточный финиш пройдут 80 велосипедистов?
Ответ: 70 байтов.
Самое главное.
При алфавитном подходе считается, что каждый символ некоторого сообщения имеет опредёленный информационный вес — несёт фиксированное количество информации.
1 бит — минимальная единица измерения информации.
Информационный объём сообщения I равен произведению количества символов в сообщении К на информационный вес символа алфавита i: I = K•i.
Байт, килобайт, мегабайт, гигабайт, терабайт — единицы измерения информации. Каждая следующая единица больше предыдущей в 1024 (210) раза.
Вопросы и задания.
1.Ознакомтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
Компьютерная грамотность с Надеждой
Заполняем пробелы — расширяем горизонты!
Единицы измерения объема информации
Для измерения длины есть такие единицы, как миллиметр, сантиметр, метр, километр. Известно, что масса измеряется в граммах, килограммах, центнерах и тоннах. Бег времени выражается в секундах, минутах, часах, днях, месяцах, годах, веках. Компьютер работает с информацией и для измерения ее объема также имеются соответствующие единицы измерения.
Бит и байт — минимальные единицы измерения информации
Мы уже знаем, что компьютер воспринимает всю информацию через нули и единички.
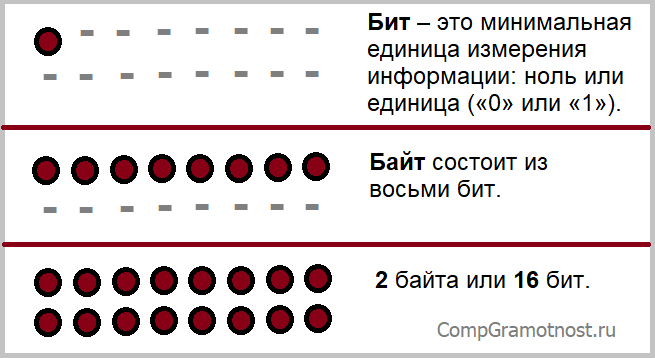
Бит – это минимальная единица измерения информации, соответствующая одной двоичной цифре («0» или «1»).
Бит — это только 0 («ноль») или только 1 («единичка»). С помощью одного бита можно записать одно из двух состояний: 0 (ноль) или 1 (один). Чтобы записать два состояния, потребуется два бита. Бит — это минимальная ячейка памяти, меньше не бывает. В этой ячейке может храниться либо нолик, либо единичка.
Байт состоит из восьми бит. Используя один байт, можно закодировать один символ из 256 возможных (256 = 2 8 ). Таким образом, один байт равен одному символу, то есть 8 битам:
1 символ = 8 битам = 1 байту.
Буква, цифра, знак препинания — это символы. Одна буква — один символ. Одна цифра — тоже один символ. Один знак препинания (либо точка, либо запятая, либо вопросительный знак и т.п.) — снова один символ. Один пробел также является одним символом.
Кроме бита и байта, конечно же, есть и другие, более крупные единицы измерения информации.
Таблица байтов:
1 Кб (1 Килобайт) = 2 10 байт = 2*2*2*2*2*2*2*2*2*2 байт =
= 1024 байт (примерно 1 тысяча байт – 10 3 байт)
1 Мб (1 Мегабайт) = 2 20 байт = 1024 килобайт (примерно 1 миллион байт – 10 6 байт)
1 Гб (1 Гигабайт) = 2 30 байт = 1024 мегабайт (примерно 1 миллиард байт – 10 9 байт)
1 Тб (1 Терабайт) = 2 40 байт = 1024 гигабайт (примерно 10 12 байт). Терабайт иногда называют тонна.
1 Пб (1 Петабайт) = 2 50 байт = 1024 терабайт (примерно 10 15 байт).
1 Эксабайт = 2 60 байт = 1024 петабайт (примерно 10 18 байт).
1 Зеттабайт = 2 70 байт = 1024 эксабайт (примерно 10 21 байт).
1 Йоттабайт = 2 80 байт = 1024 зеттабайт (примерно 10 24 байт).
Такое приближение (или округление) вполне допустимо и является общепринятым.
Ниже приводится таблица байтов с английскими сокращениями (в левой колонке):
10 3 b = 10*10*10 b= 1000 b – килобайт
10 6 b = 10*10*10*10*10*10 b = 1 000 000 b – мегабайт
10 21 b – зеттабайт
10 24 b – йоттабайт
Выше в правой колонке приведены так называемые «десятичные приставки», которые используются не только с байтами, но и в других областях человеческой деятельности. Например, приставка «кило» в слове «килобайт» означает тысячу байт. В случае с километром она соответствует тысяче метров, а в примере с килограммом она равна тысяче грамм.
Продолжение следует…
Возникает вопрос: есть ли продолжение у таблицы байтов? В математике есть понятие бесконечности, которое обозначается как перевернутая восьмерка: ∞.
Напоследок парочка примеров по устройствам, на которые можно записать терабайты и гигабайты информации.
Есть удобный «терабайтник» – внешний жесткий диск, который подключается через порт USB к компьютеру. На него можно записать терабайт информации. Особенно удобно для ноутбуков (где смена жесткого диска бывает проблематична) и для резервного копирования информации. Лучше заранее делать резервные копии информации, а не после того, как все пропало.
CD-диски могут вмещать 650 Мб, 700 Мб, 800 Мб и 900 Мб.
DVD-диски рассчитаны на большее количество информации: 4.7 Гб, 8.5 Гб, 9.4 Гб и 17 Гб.
Упражнения по компьютерной грамотности
Статья закончилась, но можно еще прочитать:
Нашли ошибку? Выделите фрагмент текста и нажмите Ctrl+Enter.
Единицы измерения количества информации
В качестве единицы информации условились принять один бит (англ. bit — binary digit — двоичная цифра). За единицу количества информации принимается такое количество информации, которое содержит сообщение, уменьшающее неопределенность в два раза. Такая единица называется бит.
Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений.
А в вычислительной технике битом называют наименьшую “порцию” памяти, необходимую для хранения одного из двух знаков “0” и “1”, используемых для внутримашинного представления данных и команд.
В 1948 году Клод Шеннон впервые ввел слово «bit» в статье «Математическая теория связи». Происхождение этого слова он приписывал Джону Тьюки, использовавшему сокращение «bit» вместо слов «binary digit» в заметке лаборатории Белла от 9 января 1947 года.
Минимальная единица
Бит — слишком мелкая единица измерения. На практике чаще применяется более крупная единица — байт, равная восьми битам. Именно восемь бит требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256 = 28).
Широко используются также более крупные производные:
1 Килобайт (Кбайт) = 1024 байт = 210 байт;
1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт;
1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт.
В последнее время в связи с увеличением объемов обрабатываемой информации входят в употребление такие производные единицы, как:
1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт;
1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт.
Укажите что принято за минимальную единицу измерения информации
Для информации существуют свои единицы измерения информации. Если рассматривать сообщения информации как последовательность знаков, то их можно представлять битами, а измерять в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах и петабайтах.
Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.
Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.
Байт – основная единица измерения количества информации.
Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.
Производные единицы измерения количества информации
1 килобайт (Кб)=1024 байта =2 10 байтов
1 мегабайт (Мб)=1024 килобайта =2 10 килобайтов=2 20 байтов
1 гигабайт (Гб)=1024 мегабайта =2 10 мегабайтов=2 30 байтов
1 терабайт (Гб)=1024 гигабайта =2 10 гигабайтов=2 40 байтов
Методы измерения количества информации
Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:
Алфавитный подход к измерению количества информации
При этом подходе отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка, т.е. его алфавит можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет в себе каждый символ:
Вероятностный подход к измерению количества информации
Этот подход применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:
I – количество информации,
N – количество возможных событий,
Pi – вероятность i-го события.
Задача 1.
Шар находится в одной из четырех коробок. Сколько бит информации несет сообщение о том, в какой именно коробке находится шар.
Имеется 4 равновероятных события (N=4).
По формуле Хартли имеем: 4=2 i . Так как 2 2 =2 i , то i=2. Значит, это сообщение содержит 2 бита информации.
Задача 2.
Чему равен информационный объем одного символа русского языка?
В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа. I=log2 N=log2 32=5 битов (2 5 =32).
Примечание. Если невозможно найти целую степень числа, то округление производится в большую сторону.
Задача 3.
Чему равен информационный объем одного символа английского языка?
Задача 4.
Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний (“включено” или “выключено”). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 N сигналов.
2 5 6 , поэтому пяти лампочек недостаточно, а шести хватит. Значит, нужно 6 лампочек.
Задача 5.
Метеостанция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
В данном случае алфавитом является множество чисел от 0 до 100, всего 101 значение. Поэтому информационный объем результатов одного измерения I=log2101. Но это значение не будет целочисленным, поэтому заменим число 101 ближайшей к нему степенью двойки, большей, чем 101. это число 128=2 7 . Принимаем для одного измерения I=log2128=7 битов. Для 80 измерений общий информационный объем равен 80*7 = 560 битов = 70 байтов.
Задача 6.
Определите количество информации, которое будет получено после подбрасывания несимметричной 4-гранной пирамидки, если делают один бросок.
Пусть при бросании 4-гранной несимметричной пирамидки вероятности отдельных событий будут равны: p1=1/2, p2=1/4, p3=1/8, p4=1/8.
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
Задача 7.
Задача 8.
Оцените информационный объем следующего предложения:
Тяжело в ученье – легко в бою!
Так как каждый символ кодируется одним байтом, нам только нужно подсчитать количество символов, но при этом не забываем считать знаки препинания и пробелы. Всего получаем 30 символов. А это означает, что информационный объем данного сообщения составляет 30 байтов или 30 * 8 = 240 битов.