Удобные числа в математике что такое
Простые и составные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Натуральные числа больше единицы бывают простые и составные.
Простое число — это натуральное число больше 1, у которого есть всего два делителя: единица и само число.
Составное число — похоже на простое. Это точно такое же натуральное число больше единицы, которое делится на единицу, на само себя и еще хотя бы на одно натуральное число.
Число 1 — не является ни простым, ни составным числом, так как у него только один делитель — 1. Именно этим оно отличается от всех остальных натуральных чисел.
Число 2 — первое наименьшее простое, единственное четное, простое число. Все остальные — нечетные.
Число 4 — первое наименьшее составное число.
В математике есть первые простые и составные числа, но последних таких чисел не существует.
А еще не существует простых чисел, которые оканчиваются на 4, 6, 8 или 0. В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.
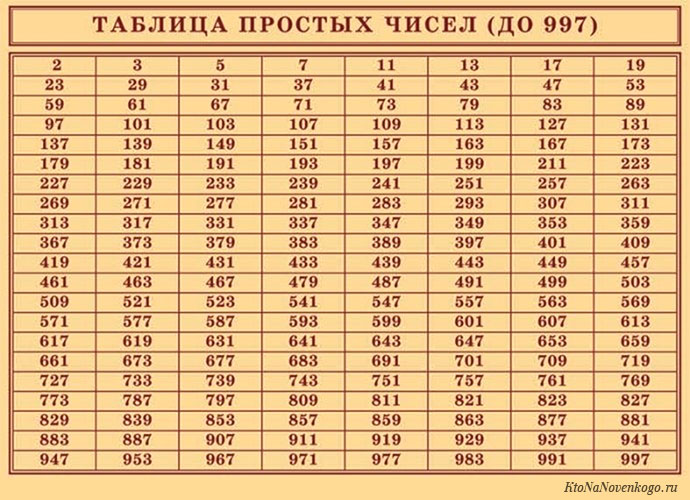
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 |
| 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 | 283 | 293 | 307 |
| 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 | 419 |
| 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 |
| 647 | 653 | 659 | 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 |
| 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 |
| 887 | 907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Простые числа — это чудеса деления
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком математическом понятии, как ПРОСТЫЕ ЧИСЛА.
В школе это проходят в 5 или 6 классе, в зависимости от программы обучения.
И интересно, что если спросить школьников, что такое простые числа, то они, скорее всего, ответят правильно.
А вот взрослые задумаются и не факт, что вспомнят точное определение. Так что это статья скорее для них.
Простые числа — это.
Итак, вот как выглядит официальное определение:
Простые числа – это такие числа, которые имеют только два делителя. Один из них – единица, а другое – само число.
Чтобы было более понятно, приведем простой пример. Для чисел 5 и 7 надо найти все возможные делители, чтобы в результате образовалось целое число.
Если вы попробуете решить эту задачку, то получите, что 5 и 7 делятся только на 1 и 5, и 1 и 7 соответственно. Во всех других случаях вы получите дробное число. И это как раз означает, что числа 5 и 7 относятся к простым.
А вот попробуем по той же схеме разобрать числа 6 и 9. В первом случае мы получим, что 6 можно поделить на 1, 2, 3 и 6, а число 9 – на 1, 3 и 9. И это уже противоречит определению простых чисел, значит, 6 и 9 таковыми не являются.
Они называются в математике – СОСТАВНЫМИ ЧИСЛАМИ.
Список и таблица простых чисел
Некоторые ошибочно полагают, что наименьшее простое число – это единица.
С одной стороны, в этом есть логика, так как 1 делится только на 1. Но это получается одно и то же число (единица), что противоречит определению простых чисел, в котором четко прописано – «делителей должно быть два».
Значит, минимальное простое число – это 2. А первоначальный ряд выглядит следующим образом:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199…
При желании можете проверить эти числа на предмет деления. Мы же скажем, что этот ряд на самом деле не окончательный.
Количество простых чисел не ограничено. Или говоря математическим языком, оно стремится к бесконечности.
История простых чисел
Первые упоминания о простых числах относятся к Древнему Египту. В Британском музее хранится папирус, который датируется 2000 годом до нашей эры. И на нем, согласно расшифровке, содержится учебное пособие по арифметике.
В том числе и про деление чисел. Называется этот артефакт – папирус Райнда, по имени его первого владельца.
В этом документе есть таблица, в которой указаны числа, делящиеся на различные знаменатели. Причем они разделены таким образом, что становится понятно – древние египтяне может и не пользовались понятиям «простое число», но хотя бы имели о нем представление.
Ну а первые исследования простых чисел датируются 300 годом до нашей эры. И связаны они с именем знаменитого древнегреческого математика Евклида.
Как и многое другое, он описал простые и составные числа в своем известном произведении «Начала».
В частности, Евклид описал такие вещи, как:
Сейчас расскажем об этих понятиях подробнее.
Основная теорема арифметики
Основная теорема арифметики, которую придумал еще Евклид, гласит:
Любое натуральное число (это что?), которое больше единицы, может быть представлено в виде произведения простых чисел. Причем их количество не ограничено, а порядок следования неважен.
Если обозначить исходное число буквой N, а простые числа буквами Р1, Р2, Р3 и так далее, то можно записать эту теорему следующим образом:
N = Р1 * Р2 * Р3 * … * РК
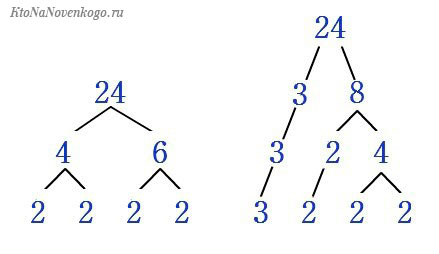
Например, возьмем число 100. Его можно разложить на следующие простые числа:
Или более сложный пример – число 23244:
23244 = 149 * 13 * 3 * 2 * 2
Раскладывать на простые числа легко. Можно сперва делить на 2 и 3, а уже в конце автоматически получить более сложные делители.
Ради интереса придумайте любое число и сами найдите его составляющие.
Лемма Евклида
Еще одна теорема, которая имеет прямое отношение к простым числам. Она гласит;
Если некое простое число Р делит произведение чисел X и Y без остатка, то оно может точно так же поделить или X, или Y.
Звучит несколько сложновато, хотя на деле все это просто. Так, возьмем для примера P = 2, X = 6, Y = 9. И тогда получается, что
В нашем примере P делит это произведение без остатка:
А значит наша P может поделить без остатка или X, или Y. Очевидно, что это X:
Y/P = 9/2 = 4,5 (не подходит)
Как быстро и легко определить простые числа
И еще одно понятие, которое связано с простыми числами. Оно названо в честь другого древнегреческого математика Эратосфена Киренского.
Этот человек придумал, как быстро и легко определить простые числа. В частности, он сделал таблицу, в которой были указаны значения до 1000.
Свою таблицу он нарисовал на глиняной дощечке. А после прокалывал те клеточки, на которых были написаны составные числа. В результате получилось нечто вроде решета, отсюда собственно и название метода.
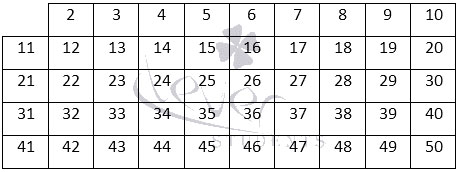
Кстати, пользоваться решетом Эратосфена весьма просто. Например, сделаем таблицу до 50.
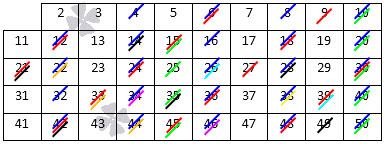
После этого из нее надо поочередно вычеркивать числа, которые кратны 2, 3, 5, 7 и 11. В результате получится вот это:
Те числа, которые остались, и есть простые. Можете сравнить этот ряд с тем, который мы давали в начале статьи. Точно таким же способом можно составить абсолютно любой ряд простых чисел = хоть до тысячи, хоть до миллиона и больше.
Вот и все, что мы хотели рассказать о ПРОСТЫХ ЧИСЛАХ в математике.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Математика весьма хитрая наука, да и простые числа не такие уж и простые, понимание простых и составных чисел привело человечество к тому техническому прогрессу, что окружает нас сейчас.
Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена
В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.
Простые и составные числа – определения и примеры
Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.
Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.
Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.
Простые числа – это натуральные числа, имеющие только два положительных делителя.
Составное число – это натуральное число, имеющее более двух положительных делителей.
Натуральные числа, которые не являются простыми, называют составными.
Таблица простых чисел
Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:
Рассмотрим теорему, которая объясняет последнее утверждение.
Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.
Простых чисел бесконечно много.
Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.
Решето Эратосфена
Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.
Перейдем к формулировке теоремы.
Данное число простое или составное?
Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.
Доказать что число 898989898989898989 является составным.
Ответ: 11723 является составным числом.
Простые числа в математике
Что такое простые числа
Простые числа — натуральное число, имеющее ровно два различных натуральных делителя — единицу и самого себя. Другими словами, число x является простым, если оно больше 1 и при этом делится без остатка только на 1 и на x.
Например, 11 — это простое число. Его можно разделить только на 1 и 11. Деление простого числа на другое приводит к тому, что остается остаток, что называют простым числом.
13 ÷ 4 = 3 (остаток 1).
Число, имеющее более двух множителей, называется составными числами. Наименьшее простое число равно 2, потому что оно делится само на себя и только на 1.
30 не является примером простого числа, потому что его можно разделить на 1,2,3,5,6,10,15,30. Таким образом, 30 является примером составного числа, поскольку оно имеет более двух факторов.
Ноль, единица и числа меньше единицы не считаются простыми числами.
Основная теорема арифметики, лемма Евклида
Основная идея теоремы арифметики — это любое целое число больше 1 либо является простым числом, либо может быть получено путем умножения простых чисел вместе.
Фундаментальная теорема арифметики (название которой указывает на ее основную важность) гласит, что любое число может быть учтено в уникальном списке простых чисел.
Простое число (2,3,5,7,11. ) против составного (4=2×2, 6=2×3, 8=2x2x2, 12=2x2x3. ).
Этот ряд примеров можно продолжить:
Таким образом, они либо простые, либо простые числа, умноженные друг на друга.
Число 42. Можем ли мы получить 42, умножив только простые числа?
Да, 2, 3 и 7 являются простыми числами, и при умножении вместе они составляют 42.
Число 7. 7 уже является простым числом
Число 22. 22 может быть получено путем умножения простых чисел 2 и 11 вместе.
Никакая другая комбинация простых чисел не будет работать.
Лемма — это, как правило, незначительное, доказанное утверждение, которое используется в качестве ступеньки к доказательству более сложной математической теории. По этой причине она также известна как «вспомогательная теорема».
В теории чисел лемма Евклида — это лемма, которая отражает фундаментальное свойство простых чисел, а именно: если простое число p делит произведение ab двух целых чисел a и b, то p должно разделить, по крайней мере, одно из этих целых чисел a и b.
Если p = 19, a = 133, b = 143, то ab = 133 × 143 = 19019, и поскольку это делится на 19, лемма подразумевает, что один или оба из 133 или 143 также должны быть. На самом деле 133 = 19 × 7.
Если предпосылка леммы не выполняется, т. е. p является составным числом, его следствие может быть либо истинным, либо ложным.
В случае p = 10, a = 4, b = 15 составное число 10 делит ab = 4 × 15 = 60, но 10 не делит ни 4, ни 15.
Это свойство является ключевым в доказательстве фундаментальной теоремы арифметики. Лемма Евклида показывает, что в целых числах неприводимые элементы также являются простыми элементами.
Таким образом, изучение чисел в основном сводится к изучению свойств простых чисел. Математики на протяжении тысячелетий довольно много выяснили о простых числах. Одно из самых известных доказательств Евклида показывает, что существует бесконечно много простых чисел.
Как определить простые числа
Сначала попробуйте разделить его на 2 и посмотреть, получится ли целое число. Если да, то оно не может быть простым числом. Если вы не получите целое число, затем попробуйте разделить его на простые числа: 3, 5, 7, 11 (9 делится на 3) и так далее, всегда делясь на простое число.
8 простых чисел до 20: 2, 3, 5, 7, 11, 13, 17 и 19.
Первые 10 простых чисел — это 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
Таблица простых чисел до 1000:
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 |
| 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 |
| 113 | 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 |
| 173 | 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 |
| 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 |
| 281 | 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 |
| 349 | 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 |
| 409 | 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 |
| 463 | 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 |
| 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 |
| 659 | 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 |
| 733 | 739 | 743 | 751 | 757 | 761 | 769 | 773 | 787 | 797 |
| 809 | 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 |
| 863 | 877 | 881 | 883 | 887 | 907 | 911 | 919 | 929 | 937 |
| 941 | 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 |
2 — наименьшее простое число. Это также единственное четное простое число — все остальные четные числа могут быть разделены сами по себе на 1 и 2, что означает, что у них будет, по крайней мере, 3 фактора.
Один из самых известных математиков классической эпохи, Евклид, записал доказательство того, что не существует самого большого простого числа. Самое большое известное простое число (по состоянию на ноябрь 2020 года) составляет 282 589 933-1, число, которое имеет 24 862 048 цифр при записи в базе 10. До этого самым большим известным простым числом было 277 232 917-1, состоящее из 23 249 425 цифр.
За исключением 2 и 3, все остальные простые числа могут быть выражены в общей форме как 6n + 1 или 6n — 1, где n — натуральное число.
Чтобы определить, является ли число простым или составным, нужно решить пример на делимость в следующем порядке (от простого к сложному): 2, 5, 3, 11, 7, и 13. Если вы обнаружите, что число делится на одно из них, и вы знаете, что оно составное, не нужно выполнять остальные тесты.
Если число меньше 121 не делится на 2, 3, 5 или 7, оно простое; в противном случае оно составное.
Если число меньше 289 не делится на 2, 3, 5, 7, 11, или 13, это простое число; в противном случае оно составное.
Примеры решения задач
Является ли 19 простым числом или нет?
Как понять, что число простое можно двумя способами.
Формула для простого числа равна 6n + 1
Запишем данное число в виде 6n + 1.
Проверьте на наличие факторов 19
Следовательно, с помощью обоих методов докажем, что 19 имеет только два фактора 1 и 19, что означает простое число.
53 — это простое число или нет?
Как доказать, что число простое, используя приведенную ниже формулу. Чтобы узнать простые числа, превышающие 40, можно:
32 + 3 + 41 = 9 + 3 + 41 = 53
53 имеет только факторы 1 и 53.
Итак, 53 является простым числом по обоим методам.
Является ли число простым или составным?
Число 185 заканчивается на 5, поэтому оно делится на 5. Оно составное.
Как проверить простое ли число 243?
Число 243 заканчивается нечетным числом, поэтому оно не делится на 2. Он не заканчивается на 5 или 0, поэтому он не делится на 5. Его цифровой корень равен 9 (потому что 2 + 4 + 3 = 9), так что оно делится на 3.
Разряды и классы чисел
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.