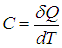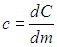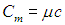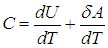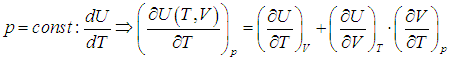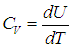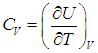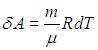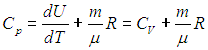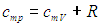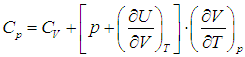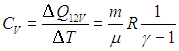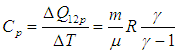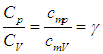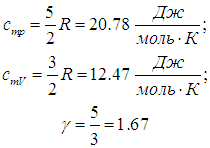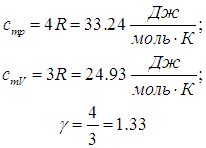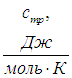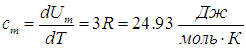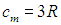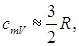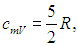Удельная теплоемкость и теплоемкость чем отличаются

Количество теплоты и удельная теплоемкость

Вместо словосочетания «тепловая энергия» физики говорят сокращенно: «теплота».

Удобно сравнивать между собой величины, которые измерены численно. Поэтому, физики говорят о количестве тепловой энергии, или количестве теплоты.

Что такое количество теплоты

Рассмотрим чашку, в которой находится обыкновенная вода комнатной температуры.

Вычислим внутреннюю энергию холодной воды в чашке, получим число, которое можно обозначить так:

\(\large U_<\text<хол>> \left( \text <Дж>\right) \) – внутренняя энергия холодной воды.

Нагреем воду в чашке. Молекулы нагретой воды будут двигаться быстрее. Значит, горячая вода обладает большим количеством внутренней энергии.

Теперь посчитаем внутреннюю энергию горячей воды в чашке. Полученное число обозначим, как

\(\large U_<\text<горяч>> \left( \text <Дж>\right) \) – внутренняя энергия горячей воды.

Найдем разницу внутренней энергии для горячей и холодной воды.

Примечание: Вместо слова «разница» математики скажут «разность».

Мы получим еще одно число. Обозначим его символом Q. Число Q называют количеством теплоты. Именно эту тепловую энергию вода получила во время нагревания.

Примечание: Когда горячая вода остынет, она отдаст ровно столько тепловой энергии, сколько получила во время нагревания. Потому, что выполняется закон сохранения тепловой энергии.

\(\large Q \left( \text <Дж>\right) \) – тепловая энергия, количество теплоты.

Теплота, как и любая энергия, измеряется в системе СИ в Джоулях, в честь английского физика Джеймса Джоуля.

Примечание: Количество теплоты, так же, измеряют в Калориях.

Калория – это тепловая энергия, затраченная на нагревание 1 грамма воды на 1 градус Цельсия.

Джоуль и Калория связаны так:

От чего зависит количество теплоты

Количество теплоты, требуемое для нагревания тела, зависит от нескольких параметров.

От массы вещества

Нальем в одну кастрюльку 1 кг воды, а в другую, точно такую же кастрюльку – 2 килограмма воды.

Пусть, начальная температура воды о обеих кастрюльках равна +20 градусам Цельсия.

Будем нагревать эти кастрюльки по очереди на газовой плите, не меняя интенсивность огня конфорки.

Предположим, нам нужно повысить на 50 градусов Цельсия температуру воды в каждой кастрюльке.

Примечание: После нагревания воды на 50 градусов, конечная температура воды в каждой кастрюльке будет равна 70 градусам.

Чтобы нагреть на 50 градусов 1 килограмм воды, потребуется время. Однако, чтобы нагреть на этой же конфорке 2 килограмма воды на 50 градусов, потребуется больше времени.

Значит, количество теплоты, полученное водой, зависит от массы вещества, которое мы хотим нагреть.

Математики запишут фразу «количество теплоты зависит от массы» так:

Символом f обозначается зависимость.

\(\large m \left( \text <кг>\right) \) – масса нагреваемого вещества.

От разницы температур

Теперь возьмем две кастрюльки, и нальем в них по 1 кг воды. Начальная температура воды в кастрюльках одинаковая и равна +20 градусов Цельсия.

Одну кастрюльку будем нагревать дольше другой. Поэтому, температура воды будет выше в той кастрюльке, которую дольше нагревали.

Так как температура повысилась больше в кастрюльке, которую дольше нагревали, то физики скажут, что воде в этой кастрюльке передали большее количество теплоты.

Значит, количество теплоты зависит от разницы (т. е. разности) между начальной и конечной температурой.

\(\large t_<\text<конеч>> \left( \text <град>\right) \) – температура после нагревания;

\(\large t_<\text<нач>> \left( \text <град>\right) \) – температура до нагревания;

\(\large \Delta t \left( \text <град>\right) \) – разность температуры;

Математики фразу «количество теплоты зависит от разности температур» запишут так:

Символ f обозначает, что Q зависит от разницы температур.

От вида вещества

Теперь будем нагревать 1 килограмм воды и 1 килограмм подсолнечного масла.

Первоначальная температура каждого вещества +20 градусов Цельсия.

Измерим через 5 минут нагревания температуру воды и температуру масла.

Оказывается, за 5 минут масло нагреется до более высокой температуры. При этом и масло, и вода, получили одинаковое количество теплоты.

Значит, количество теплоты зависит от того, из какого вещества состоит тело.

Какие величины называют удельными

Физики часто применяют удельные величины, так как они достаточно удобны для вычислений.

Удельная величина – величина, приходящаяся на единицу массы, длины, площади, или объема.

В обычной жизни мы, так же, пользуемся удельными величинами. К примеру, цена товара – это удельная величина, так как она приходится на единицу товара. Зная количество товара, легко посчитать общую цену покупки.

Например, булочка стоит 20 рублей. Нужно купить 3 булочки. Общую сумму денег найдем, перемножив цену одной булочки (удельную величину) на количество штук.

Известно, что при горении топлива выделяется энергия. Удельная теплота сгорания и количество сгоревших килограммов топлива помогут посчитать выделившуюся тепловую энергию.

Что такое удельная теплоемкость

Возьмем 1 килограмм вещества и нагреем его на 1 градус Цельсия. Тепловая энергия, которую мы для этого затратили, называется удельной теплоемкостью.

Удельная теплоемкость – это энергия, затраченная для нагревания 1 килограмма на 1 градус.

Эту энергию обозначают латинским символом «c». Измеряют ее в Джоулях, деленных на килограмм и градус.

\(\large c \left( \frac<\text<Дж>> <\text<кг>\cdot \text<град>> \right) \) – удельная теплоемкость;

Примечания:

Удельные теплоемкости воды в различных агрегатных состояниях

В твердом состоянии (лед), вода будет иметь такую теплоемкость:

В жидком состоянии (вода), такую:

В газообразном состоянии (пар) при температуре 100 градусов Цельсия, такую:

Примечание: Удельные теплоемкости различных веществ можно найти в школьном справочнике физики.

Как связаны и чем отличаются количество теплоты и удельная теплоемкость

Будем рассматривать такие процессы, как нагревание и охлаждение.

Благодаря процессам нагревания и охлаждения мы можем обогреваться зимой с помощью русской печи. Сначала печь получит количество теплоты (тепловую энергию) от сгорающего топлива — дров. А затем, будет остывать и отдавать это количество теплоты всем телам, находящимся в помещении.

Отличия удельной теплоемкости от количества теплоты

Запомнить, что такое количество теплоты, и чем оно отличается от удельной теплоемкости, можно так (рис. ):

Связь количества теплоты и удельной теплоемкости — формула

то легко посчитать общую тепловую энергию – т. е. количество теплоты.

Для этого используем формулу:

\(\large Q \left( \text <Дж>\right) \) – количество теплоты, т. е. общая тепловая энергия;

\(\large c \left( \frac<\text<Дж>> <\text<кг>\cdot \text<град>> \right) \) – удельная теплоемкость;

\(\large m \left( \text <кг>\right) \) – масса вещества;

\(\large t_<\text<конеч>> \left( \text <град>\right) \) – температура после нагревания;

\(\large t_<\text<нач>> \left( \text <град>\right) \) – температура до нагревания;

Как по графику нагревания или охлаждения определить удельную теплоемкость

На примере покажем, как находить удельную теплоемкость по графику нагревания или охлаждения тела.

Дано твердое тело массой 2 килограмма. На рисунке 5 указано, как зависит температура этого тела от полученного количества теплоты. По горизонтали отложено количество теплоты, а по вертикали – температура некоторого тела, находящегося в твердом состоянии.

Определить удельную теплоемкость вещества, из которого состоит данное твердое тело.

Решение:

Тело нагрелось от \(\large t_ <1>= 0 \left( С \right) \) до температуры \(\large t_ <2>= 60 \left( С \right) \);

Разность температур равна 60 градусам Цельсия.

Масса тела 2 килограмма.

Полученное количество теплоты \(\large Q = 15000 \left( \text <Дж>\right) \).

Выпишем формулу, по которой можно посчитать тепловую энергию Q:

Подставим теперь значения в эту формулу для определения количества теплоты:

\[\large 15000 = c \cdot 2 \cdot 60 \]

Разделим обе части уравнения на число 10:

\[\large 1500 = c \cdot 2 \cdot 6 \]

Теперь разделим обе части уравнения на число 6:

\[\large 250 = c \cdot 2 \]

Разделив обе части на число 2, получим удельную теплоемкость твердого вещества:

Ответ: Удельная теплоемкость твердого вещества \(\large 125 \left( \frac<\text<Дж>> <\text<кг>\cdot \text<град>> \right) \)

Примечание: Тела могут обмениваться тепловой энергией с другими телами. Обмен энергией прекратится при наступлении теплового равновесия. Для решения задач нужно использовать удельные теплоемкости материалов, из которых изготовлены тела. А чтобы рассчитать переданное или полученное телом количество теплоты, нужно уметь применять закон сохранения энергии и составлять уравнение теплового баланса.

Источник

Разница между удельной теплоемкостью и теплоемкостью

Главное отличие

Тепло — это одна из форм энергии, когда два объекта взаимодействуют, передача этой энергии от одного тела к другому весьма вероятна. Тепловая энергия прямо пропорциональна температуре, это означает, что повышение температуры автоматически приводит к увеличению тепловой энергии внутри тела и наоборот. Оба эти термина, удельная теплоемкость и теплоемкость, широко используются в термодинамике, поскольку оба относятся к энергии, необходимой для повышения температуры объекта. Удельная теплоемкость и теплоемкость очень похожи друг на друга с разницей в дополнительной переменной в удельной теплоемкости. Хотя многие люди используют эти термины как синонимы, поскольку их концепция в совокупности описывается как «удельная теплоемкость». Чтобы понять разницу между обоими этими терминами, необходимо знать о дополнительной переменной удельной теплоемкости. C ) или 1 Кельвин, тогда как удельная теплоемкость — это количество тепла, необходимое для повышения температуры вещества массой 1 кг или 1 г на 1 градус Цельсия (° C ) или 1 Кельвин.

Сравнительная таблица

Что такое удельная теплоемкость?

где
Q — добавленное тепло,
C — удельная
теплоемкость, ∆T — изменение температуры.

Это соотношение не остается в силе, когда происходит фазовый переход, что означает преобразование воды в газообразное состояние (точка кипения) или когда лед превращается в жидкое состояние (точка плавления. Это происходит потому, что тепло, отводимое или добавляемое во время фазового перехода, не приводить к изменению температуры.Когда речь идет о теоретической или лабораторной работе, используется удельная теплоемкость, а не теплоемкость, поскольку она также измеряет массу вещества или объекта.

Что такое теплоемкость?

Теплоемкость — это количество тепла, необходимое для повышения температуры вещества до 1 градуса Цельсия (° C) или 1 Кельвина. Втянутое тепло или повышение температуры не имеют ничего общего с массой вещества. Тепловая энергия прямо пропорциональна температуре, это означает, что повышение температуры автоматически приводит к увеличению тепловой энергии внутри тела и наоборот. Теплоемкость можно определить с помощью этого уравнения:

Где
Δ «> Δ Q — количество добавленного тепла,
C — удельная ТЕПЛО,
Δ «> Δ T — изменение температуры.

Источник

Удельная теплоемкость вещества

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Нагревание и охлаждение

Эти два процесса знакомы каждому. Вот нам захотелось чайку, и мы ставим чайник, чтобы нагреть воду. Или ставим газировку в холодильник, чтобы охладить.

Логично предположить, что нагревание — это увеличение температуры, а охлаждение — ее уменьшение. Все, процесс понятен, едем дальше.

Но не тут-то было: температура меняется не «с потолка». Все завязано на таком понятии, как количество теплоты. При нагревании тело получает количество теплоты, а при нагревании — отдает.

В процессах нагревания и охлаждения формулы для количества теплоты выглядят так:

Нагревание

Охлаждение

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

В этих формулах фигурирует и изменение температуры, о котором мы сказали выше, и удельная теплоемкость, речь о которой пойдет дальше.

А вот теперь поговорим о видах теплопередачи.

Виды теплопередачи

Здесь все совсем несложно, их всего три: теплопроводность, конвекция и излучение.

Теплопроводность

Тот вид теплопередачи, который можно охарактеризовать, как способность тел проводить энергию от более нагретого тела к менее нагретому.

Речь о том, чтобы передать тепло с помощью соприкосновения. Признавайтесь, грелись же когда-нибудь возле батареи. Если вы сидели к ней вплотную, то согрелись вы благодаря теплопроводности. Обниматься с котиком, у которого горячее пузо, тоже эффективно.

Порой мы немного перебарщиваем с возможностями этого эффекта, когда на пляже ложимся на горячий песок. Эффект есть, только не очень приятный. Ну а ледяная грелка на лбу дает обратный эффект — ваш лоб отдает тепло грелке.

Конвекция

Когда мы говорили о теплопроводности, мы приводили в пример батарею. Теплопроводность — это когда мы получаем тепло, прикоснувшись к батарее. Но все вещи в комнате к батарее не прикасаются, а комната греется. Здесь вступает конвекция.

Дело в том, что холодный воздух тяжелее горячего (холодный просто плотнее). Когда батарея нагревает некий объем воздуха, он тут же поднимается наверх, проходит вдоль потолка, успевает остыть и спуститься обратно вниз — к батарее, где снова нагревается. Таким образом, вся комната равномерно прогревается, потому что все более горячие потоки сменяют все менее холодные.

Излучение

Пляж мы уже упоминали, но речь шла только о горячем песочке. А вот тепло от солнышка — это излучение. В этом случае тепло передается через волны.

Обоими способами. То тепло, которое мы ощущаем непосредственно от камина (когда лицу горячо, если вы расположились слишком близко к камину) — это излучение. А вот прогревание комнаты в целом — это конвекция.

Удельная теплоемкость: понятие и формула для расчета

Формулы количества теплоты для нагревания и охлаждения мы уже разбирали, но давайте еще раз:

Нагревание

Охлаждение

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

В этих формулах фигурирует такая величина, как удельная теплоемкость. По сути своей — это способность материала получать или отдавать тепло.

С точки зрения математики удельная теплоемкость вещества — это количество теплоты, которое надо к нему подвести, чтобы изменить температуру 1 кг вещества на 1 градус Цельсия:

Удельная теплоемкость вещества

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

Также ее можно рассчитать через теплоемкость вещества:

Удельная теплоемкость вещества

c — удельная теплоемкость вещества [Дж/кг*˚C]

C — теплоемкость вещества [Дж/˚C]

Величины теплоемкость и удельная теплоемкость означают практически одно и то же. Отличие в том, что теплоемкость — это способность всего вещества к передаче тепла. То есть формулу количества теплоты для нагревания тела можно записать в таком виде:

Количество теплоты, необходимое для нагревания тела

Q — количество теплоты [Дж]

c — удельная теплоемкость вещества [Дж/кг*˚C]

t_{конечная} — конечная температура [˚C]

t_{начальная} — начальная температура [˚C]

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Таблица удельных теплоемкостей

Удельная теплоемкость — табличная величина. Часто ее указывают в условии задачи, но при отсутствии в условии — можно и нужно воспользоваться таблицей. Ниже приведена таблица удельных теплоемкостей для некоторых (многих) веществ.

Источник

Теплоёмкость

Единица измерения теплоёмкости в системе СИ — Дж/К.

Содержание

Удельная теплоёмкость

Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество вещества может быть измерено в килограммах, кубических метрах и молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают массовую, объёмную и молярную теплоёмкость.

Массовая теплоёмкость ( С ) — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на килограмм на кельвин (Дж·кг −1 ·К −1 ).

Объёмная теплоёмкость ( С′ ) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на кубический метр на кельвин (Дж·м −3 ·К −1 ).

Молярная теплоёмкость ( С_μ ) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на моль на кельвин (Дж/(моль·К)).

Теплоёмкость для различных состояний вещества

Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).

Для примера, в молекулярно-кинетической теории газов показывается, что молярная теплоёмкость идеального газа с i степенями свободы при постоянном объёме (для одного моля идеального газа) равна:

А при постоянном давлении

Удельные теплоёмкости многих веществ приведены в справочниках обычно для процесса при постоянном давлении. К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда — 2100 Дж/(кг·К).

Теория теплоёмкости

Существует несколько теорий теплоёмкости твердого тела:

Теплоёмкость системы невзаимодействующих частиц (например, газа) определяется числом степеней свободы частиц.

См. также

Полезное

Смотреть что такое «Теплоёмкость» в других словарях:

теплоёмкость — теплоёмкость, и … Русский орфографический словарь

теплоёмкость — теплоёмкость … Словарь употребления буквы Ё

ТЕПЛОЁМКОСТЬ — количество теплоты, поглощаемой телом при нагревании на 1 градус (1°С или 1К); точнее отношение кол ва теплоты, поглощаемой телом при бесконечно малом изменении его темп ры, к этому изменению. Т. ед. массы в ва (г, кг) наз. удельной Т., 1 моля в… … Физическая энциклопедия

теплоёмкость — теплоёмкость, теплоёмкости, теплоёмкости, теплоёмкостей, теплоёмкости, теплоёмкостям, теплоёмкость, теплоёмкости, теплоёмкостью, теплоёмкостями, теплоёмкости, теплоёмкостях (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов

ТЕПЛОЁМКОСТЬ — физ. величина, характеризующая тепловые свойства тела и равная отношению количества теплоты, полученного телом при бесконечно малом изменении его состояния в каком либо процессе, к вызванному им изменению температуры, т. е. теплоёмкость С = d Q/d … Большая политехническая энциклопедия

ТЕПЛОЁМКОСТЬ — ТЕПЛОЁМКОСТЬ, теплоёмкости, мн. нет, жен. (физ.). Количество тепла, необходимое для того, чтобы нагреть данное тело на 1°. Удельная теплоёмкость (количество тепла, необходимое для того, чтоб нагреть 1 г на 1°). Толковый словарь Ушакова. Д.Н.… … Толковый словарь Ушакова

теплоёмкость — и; ж. Физ. Количество теплоты, поглощаемой телом при нагревании на 1 градус (по Цельсию) или отдаваемой при остывании на 1 градус (по Цельсию). Т. металла, пластмассы. Удельная т. (количество теплоты, потребное для нагревания 1 грамма вещества на … Энциклопедический словарь

ТЕПЛОЁМКОСТЬ — ТЕПЛОЁМКОСТЬ, и, жен. (спец.). Количество теплоты (во 2 знач.), необходимое для нагревания данного тела на 1°. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

Теплоёмкость — горных пород (a. heat capacity of rocks; н. Warmekapazitat der Gesteine; ф. capacite calorifique des roches; и. capacidad termica de rocas) свойство г. п. аккумулировать тепло. Удельной Т. С наз. кол во энергии, необходимое для повышения… … Геологическая энциклопедия

теплоёмкость — сущ., кол во синонимов: 1 • теплоемкость (1) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

теплоёмкость — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN heat capacitythermal capacity … Справочник технического переводчика

Источник

2.3. Теплоемкость системы

Введем теперь очень важную термодинамическую характеристику, называемую теплоемкостью системы (традиционно обозначается буквой С с различными индексами).

Теплоемкость системы — это физическая величина, равная количеству теплоты, которое необходимо передать системе, чтобы увеличить ее температуру на один кельвин (градус):

Теплоемкость — величина аддитивная, она зависит от количества вещества в системе. Поэтому вводят также удельную теплоемкость

Удельная теплоемкость — это теплоемкость единицы массы вещества

и молярную теплоемкость

Молярная теплоемкость — это теплоемкость одного моля вещества

Поскольку количество теплоты не есть функция состояния и зависит от процесса, теплоемкость также будет зависеть от способа подвода тепла к системе. Чтобы понять это, вспомним первое начало термодинамики. Разделив равенство ( 2.4 ) на элементарное приращение абсолютной температуры dT, получим соотношение

Второе слагаемое, как мы убедились, зависит от вида процесса. Отметим, что в общем случае неидеальной системы, взаимодействием частиц которой (молекул, атомов, ионов и т. п.) пренебречь нельзя (см., например, § 2.5 ниже, в котором рассматривается ван–дер–ваальсовский газ), внутренняя энергия зависит не только от температуры, но и от объема системы. Это объясняется тем, что энергия взаимодействия зависит от расстояния между взаимодействующими частицами. При изменении объема системы меняется концентрация частиц, соответственно, меняется среднее расстояние между ними и, как следствие, меняется энергия взаимодействия и вся внутренняя энергия системы. Другими словами, в общем случае неидеальной системы

.

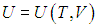
Поэтому, в общем случае первое слагаемое нельзя писать в виде полной производной, полную производную необходимо заменить на частную производную с дополнительным указанием на то, при какой постоянной величине она вычисляется. Например, для изохорного процесса:

.

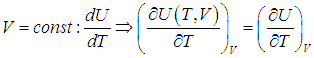
Или для изобарного процесса

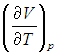
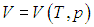
Входящая в это выражение частная производная вычисляется с помощью уравнения состояния системы, записанного в виде . Например, в частном случае идеального газа

,

эта производная равна

.

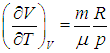
Мы рассмотрим два частных случая, соответствующих процессу подведения теплоты:

В первом случае работа dА = 0 и мы получаем теплоемкость С_V идеального газа при постоянном объеме:

С учетом сделанной выше оговорки, для неидеальной системы соотношение (2.19) необходимо записать в следующем общем виде

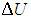
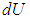
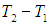
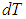
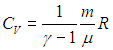
Заменив в 2.7 на , а на немедленно получаем:

.

Для вычисления теплоемкости идеального газа С_p при постоянном давлении (dp = 0) мы учтем, что из уравнения ( 2.8 ) следует выражение для элементарной работы при бесконечно малом изменении температуры

Разделив это уравнение на число молей вещества в системе, получаем аналогичное соотношение для молярных теплоемкостей при постоянном объеме и давлении, называемое соотношением Майера

Приведем для справки общую формулу — для произвольной системы — связывающую изохорную и изобарную теплоемкости:

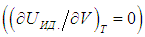
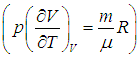
Выражения (2.20) и (2.21) получаются из этой формулы путем подстановки в неё выражения для внутренней энергии идеального газа и использования его уравнения состояния (см. выше):

.

Теплоемкость данной массы вещества при постоянном давлении больше теплоемкости при постоянном объеме, так как часть подведенной энергии тратится на совершение работы и для такого же нагревания требуется подвести больше теплоты. Отметим, что из (2.21) следует физический смысл газовой постоянной:

Газовая постоянная R — это работа, совершаемая молем идеального газа при повышении его температуры на 1 К при постоянном давлении.

Таким образом, теплоемкость оказывается зависящей не только от рода вещества, но и от условий, в которых происходит процесс изменения температуры.

Как мы видим, изохорная и изобарная теплоемкости идеального газа от температуры газа не зависят, для реальных веществ эти теплоемкости зависят, вообще говоря, также и от самой температуры Т.

Изохорную и изобарную теплоемкости идеального газа можно получить и непосредственно из общего определения, если воспользоваться полученными выше формулами ( 2.7 ) и ( 2.10 ) для количества теплоты, получаемого идеальным газом при указанных процессах.

Для изохорного процесса выражение для С_V следует из ( 2.7 ):

Для изобарного процесса выражение для С_р вытекает из ( 2.10 ):

Для молярных теплоемкостей отсюда получаются следующие выражения

Отношение теплоемкостей равно показателю адиабаты:

На термодинамическом уровне нельзя предсказать численное значение g; нам удалось это сделать лишь при рассмотрении микроскопических свойств системы (см. выражение ( 1.19 ), а также ( 1.28 ) для смеси газов). Из формул ( 1.19 ) и (2.24) следуют теоретические предсказания для молярных теплоемкостей газов и показателя адиабаты.

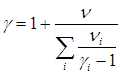
Одноатомные газы (i = 3):

Двухатомные газы (i = 5):

Многоатомные газы (i = 6):

Экспериментальные данные для различных веществ приведены в таблице 1.

Таблица 1

Видно, что простая модель идеальных газов в целом неплохо описывает свойства реальных газов. Обращаем внимание, что совпадение было получено без учета колебательных степеней свободы молекул газа.

Мы привели также значения молярной теплоемкости некоторых металлов при комнатной температуре. Если представить кристаллическую решетку металла как упорядоченный набор твердых шариков, соединенных пружинками с соседними шариками, то каждая частица может только колебаться в трех направлениях (i_кол = 3), и с каждой такой степенью свободы связаны кинетическая k_ВТ/2 и такая же потенциальная энергия. Поэтому на частицу кристалла приходится внутренняя (колебательная) энергия k_ВТ. Умножая на число Авогадро, получим внутреннюю энергию одного моля

откуда вытекает значение молярной теплоемкости

(Вследствие малого коэффициента теплового расширения твердых тел для них не различают с_р и c_v). Приведенное соотношение для молярной теплоемкости твердых тел называется законом Дюлонга и Пти, и из таблицы видно хорошее совпадение расчетного значения

Говоря о неплохом соответствии приведенных соотношений и данных опытов, следует отметить, что оно наблюдается лишь в определенном диапазоне температур. Иначе говоря, теплоемкость системы зависит от температуры, и формулы (2.24) имеют ограниченную область применения. Рассмотрим сначала рис. 2.10, на котором изображена экспериментальная зависимость теплоемкости с_тV газообразного водорода от абсолютной температуры Т.

Рис. 2.10. Молярная теплоемкость газообразного водорода Н₂ при постоям ном объеме как функция температуры (экспериментальные данные)

Ниже, для краткости, говорится об отсутствии у молекул тех или иных степеней свободы в определенных температурных интервалах. Еще раз напомним, что речь в действительности идет о следующем. По квантовым причинам, относительный вклад во внутреннюю энергию газа отдельных видов движения действительно зависит от температуры и в определенных температурных интервалах может быть мал настолько, что в эксперименте — всегда выполняемом с конечной точностью — он незаметен. Результат эксперимента выглядит так, как будто этих видов движения нет, нет и соответствующих степеней свободы. Число и характер степеней свободы определяются структурой молекулы и трехмерностью нашего пространства — от температуры они зависеть не могут.

Вклад во внутреннюю энергию от температуры зависит и может быть мал.

При температурах ниже 100 К теплоемкость

что указывает на отсутствие у молекулы как вращательных, так и колебательных степеней свободы. Далее с ростом температуры теплоемкость быстро возрастает до классического значения

характерного для двухатомной молекулы с жесткой связью, в которой нет колебательных степеней свободы. При температурах свыше 2 000 К теплоемкость обнаруживает новый скачок до значения

Этот результат свидетельствует о появлении еще и колебательных степеней свободы. Но все это пока выглядит необъяснимым. Почему молекула не может вращаться при низких температурах? И почему колебания в молекуле возникают лишь при очень высоких температурах? В предыдущей главе дано краткое качественное рассмотрение квантовых причин подобного поведения. А сейчас можно лишь повторить, что все дело сводится к специфически квантовым явлениям, не объяснимым с позиций классической физики. Эти явления подробно рассмотрены в последующих разделах курса.

http://www.plib.ru/library/book/14222.html — Яворский Б.М., Детлаф А.А. Справочник по физике, Наука, 1977 г. — стр. 236 — таблица характеристических температур «включения» колебательных и вращательных степеней свободы молекул для некоторых конкретных газов;

Обратимся теперь к рис. 2.11, представляющему зависимость молярных теплоемкостей трех химических элементов (кристаллов) от температуры. При высоких температурах все три кривые стремятся к одному и тому же значению

соответствующему закону Дюлонга и Пти. Свинец (Рb) и железо (Fe) практически имеют это предельное значение теплоемкости уже при комнатной температуре.

Для алмаза же (С) такая температура еще не достаточно высока. А при низких температурах все три кривые демонстрируют значительное отклонение от закона Дюлонга и Пти. Это еще одно проявление квантовых свойств материи. Классическая физика оказывается бессильной объяснить многие наблюдаемые при низких температурах закономерности.

Источник