сколько диагоналей можно провести в девятиугольнике
Мерзляк 5 класс — § 13. Многоугольники. Равные фигуры
Вопросы к параграфу
1. Какая фигура ограничивает многоугольник? — Замкнутая ломаная, звенья которой не пересекаются.
2. Могут ли звенья ломаной, ограничивающей многоугольник, пересекаться? — Нет, не могут.
3. Какие элементы многоугольника вы знаете? — Вершина, сторона, углы многоугольника.
4. Как называют и обозначают многоугольник? — Многоугольники называют и обозначают по его вершинам. Чтобы записать название многоугольника, надо последовательно записать все его вершины.
5. Что называют периметром многоугольника? — Периметр многоугольника — это сумма длин все его сторон.
6. Какие многоугольники называют равными? — Многоугольники называют равными, если они совпадают при наложении.
7. Какие фигуры называют равными? — Фигуры называют равными, если они совпадают при наложении.
Решаем устно
1. Сумму чисел 24 и 18 уменьшите на 33.
(24 + 18) — 33 = 42 — 33 = 9
2. Разность чисел 30 и 14 увеличьте в 3 раза.
3. Произведение чисел 12 и 5 увеличьте на 19.
(12 • 5) + 19 = 60 + 19 = 79
4. Частное чисел 189 и 9 уменьшите в 7 раз.
(189 : 9) : 7 = 21 : 7 = 3
5. Укажите среди данных отрезков равные, если:
Ответ: АВ = TQ и EF = MN.
Упражнения
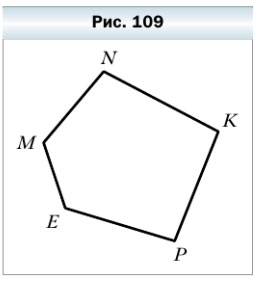
321. Назовите вершины и стороны пятиугольника, изображённого на рисунке 109.
323. Вычислите периметр пятиугольника, стороны которого равны 2 см, 4 см, 5 см 5 мм, 6 см, 7 см.
Периметр многоугольника равен сумме длин его сторон.
2 см + 4 см + 5 см 5 мм + 6 см + 7 см = 24 см 5 мм — периметр данного пятиугольника.
324. Вычислите периметр шестиугольника, три стороны которого равны по 8 см, а три другие — по 10 см.
Периметр многоугольника равен сумме длин его сторон.
8 • 3 + 10 • 3 = 24 + 30 = 54 (см) — периметр данного шестиугольника.
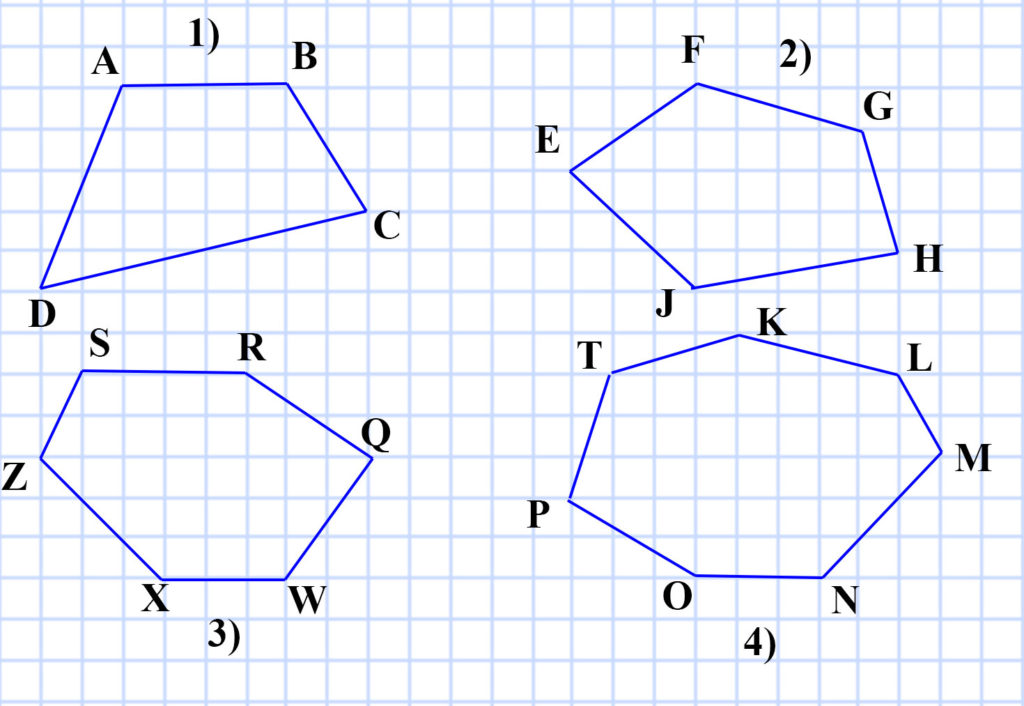
325. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 110.
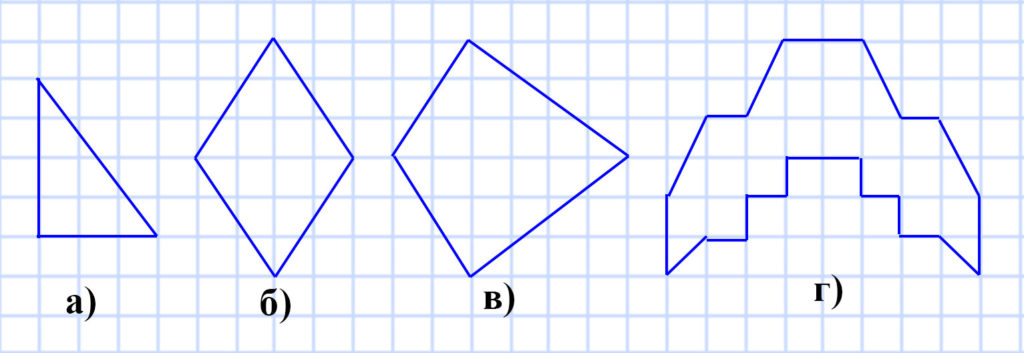
326. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 111.
327. Одна из сторон четырёхугольника равна 8 см, вторая сторона в 3 раза больше первой, а третья — на 7 см меньше второй и на 9 см больше четвёртой. Вычислите периметр четырёхугольника.
1) 8 • 3 = 24 (см) — длина второй стороны четырёхугольника.
2) 24 — 7 = 17 (см) — длина третьей стороны четырёхугольника.
3) 17 — 9 = 8 (см) — длина четвёртой стороны четырёхугольника.
4) 8 + 24 + 17 + 8 = 57 (см) — периметр четырёхугольника.
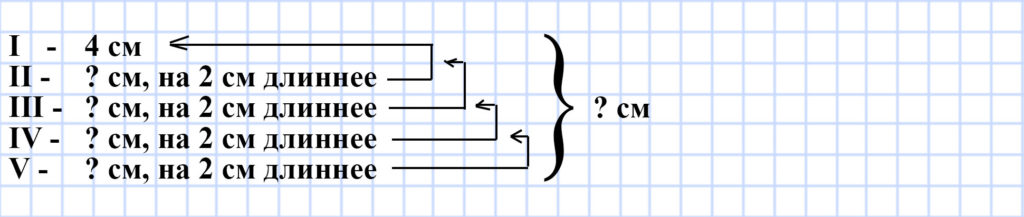
328. Стороны пятиугольника пронумеровали. Первая сторона равна 4 см, а каждая следующая сторона на 2 см длиннее предыдущей. Вычислите периметр пятиугольника.
1) 4 + 2 = 6 (см) — длина второй стороны пятиугольника.
2) 6 + 2 = 8 (см) — длина третьей стороны пятиугольника.
3) 8 + 2 = 10 (см) — длина четвёртой стороны пятиугольника.
4) 10 + 2 = 12 (см) — длина пятой стороны пятиугольника.
5) 4 + 6 + 8 + 10 + 12 = 40 (см) — периметр пятиугольника.
329. 1) Сколько диагоналей можно провести из одной вершины: а) пятиугольника; б) девятиугольника; в) и-угольника, где п > 3?
а) Из одной вершины пятиугольника можно провести 2 диагонали.
б) Из одной вершины девятиугольника можно провести 6 диагоналей.
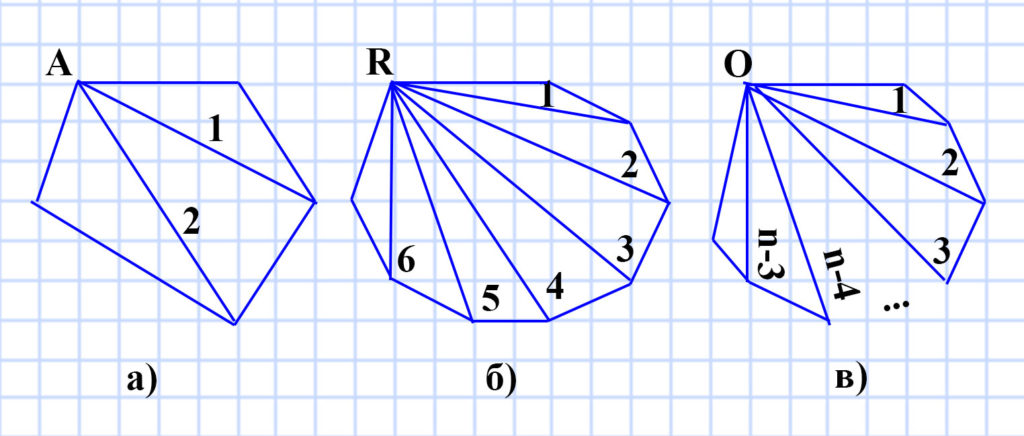
в) Из одной вершины n-угольника можно провести (n-3) диагоналей, так как:
2) Сколько всего диагоналей можно провести: а) в пятиугольнике; б) в девятиугольнике; в) в и-угольнике, где п > 3?
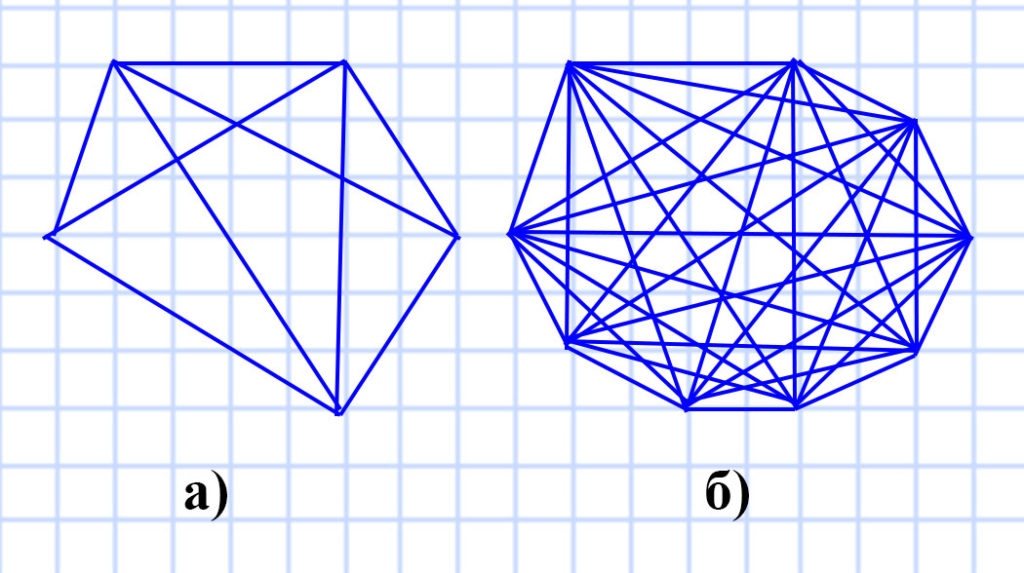
а) Мы знаем, что из одной вершины пятиугольника можно провести 2 диагонали (n-3), Значит из 5 вершин можно провести 5 • 2 = 10 диагоналей (n • (n-3)). Но если провести все 10 диагоналей, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в пятиугольнике можно провести 10 : 2 = 5 диагоналей ((n •(n-3) : 2). Рисунок подтверждает наш вывод.
б) Мы знаем, что из одной вершины девятиугольника можно провести 6 диагоналей (n-3 = 9 — 3 = 6), Значит из 9 вершин можно провести 9 • 6 = 54 диагонали (n • (n-3) = 9 • (9 — 3) = 9 • 6 = 54). Но если провести все 54 диагонали, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в девятиугольнике можно провести 54 : 2 = 27 диагоналей ((n • (n-3) : 2 = 9 • (9 — 3) : 2 = 9 • 6 : 2 = 54 : 2 = 27). Рисунок подтверждает наш вывод.
в) Исследуя предыдущие два задания мы вывели формулу, по которой можно посчитать количество возможных диагоналей в n-угольнике, при n > 3: n • (n-3) : 2. Это значит, у количество диагоналей:
Ответ: 5, 27, n • (n-3) : 2.
330. Как, используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2°?
Для того, чтобы используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2° надо:
331. Как построить угол, градусная мера которого 1°, используя шаблон угла, градусная мера которого равна:
а) 19°
Для того, чтобы используя шаблон угла, градусная мера которого 19°, построить угол, градусная мера которого равна 1° надо:
Для того, чтобы используя шаблон угла, градусная мера которого 7°, построить угол, градусная мера которого равна 1° надо:
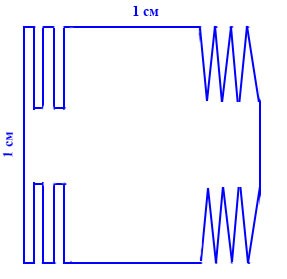
332. Существует ли многоугольник с периметром, равным 1 000 000 см, который можно целиком расположить в квадрате со стороной 1 см?
Да, теоретически такой многоугольник существует. Для этого надо из квадрата со стороной 1 см вырезать множество полосок либо треугольников, либо ещё каких-нибудь фигур вдоль нескольких сторон исходного квадрата. Точное количество таких вырезанных фигур будет зависеть от длины вырезаемых из квадрата сторон фигуры, а также от длины оставшихся от исходного квадрата сторон.
В реальности такую операцию способны выполнить только суперточные приборы, например лазерный принтер. Кроме того, необходимо провести очень точный расчёт вырезаемых фигур.
Упражнения для повторения
333. Сравните:
1) 3 986 г и 4 кг: 4 кг = 4000 г ⇒ 3 986 г
2) 6 м и 712 см: 6 м = 600 см ⇒ 600 см
3) 60 см и 602 мм: 60 см = 600 мм ⇒ 600 мм
4) 999 кг и 10 ц: 10 ц = 1000 кг ⇒ 999 кг
334. Выполните сложение, выбирая удобный порядок вычислений:
1) (636 + 927) + 364 = (636 + 364) + 927 = 1 000 + 927 = 1 927
2) (425 + 798) + 675 = (425 + 675) + 798 = 1 100 + 798 = 1 898
3) 212 + 493 + 788 + 807 = (212 + 788) + (493 + 807) = 1 000 + 1 300 = 2 300
4) 161 + 455 + 839 + 945 = (161 + 839) + (455 + 945) = 1 000 + 1 400 = 2 400
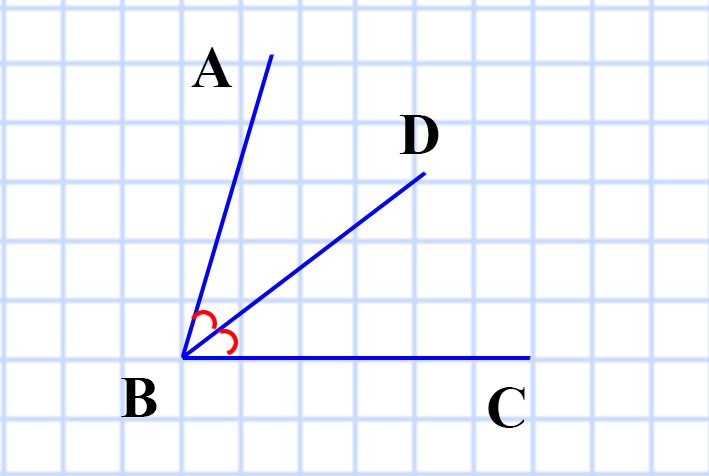
335. Известно, что ∠ABC = 74°, а луч BD — его биссектриса. Вычислите величину угла DBC.
Мы знаем, что биссектриса угла всегда делит угол пополам. Значит:
∠DBC = ∠ABC : 2 = 74° : 2 = 37°
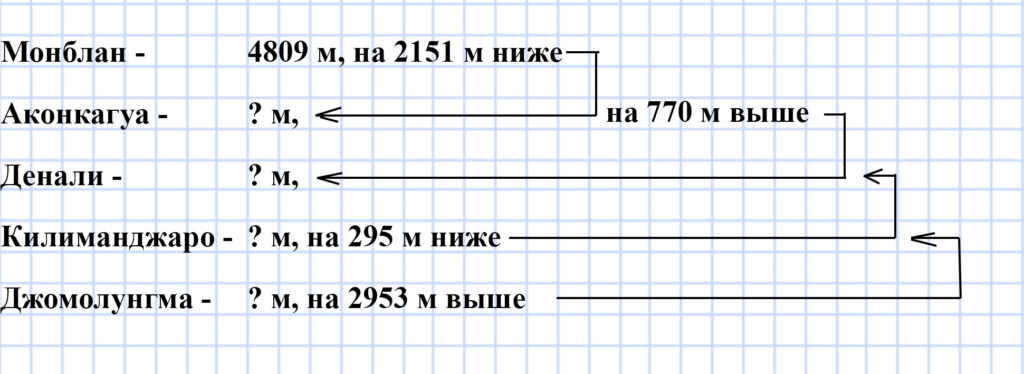
336. Высота самой высокой горы Западной Европы Монблан равна 4 809 м. Она на 2 151 м ниже самой высокой горы Южной Америки Аконкагуа, которая на 770 м выше самой высокой горы Северной Америки Денали. Какова высота самой высокой горы Африки Килиманджаро, если она на 295 м ниже горы Денали? Какова высота самой высокой горы мира Джомолунгмы (Эверест) (рис. 112), если она на 2 953 м выше горы Килиманджаро?
1) 4 809 + 2 151 = 6 960 (м) — высота горы Аконкагуа.
2) 6 960 — 770 = 6 190 (м) — высота горы Денали.
3) 6 190 — 295 = 5 895 (м) — высота горы Килиманджаро.
4) 5 895 + 2 953 = 8 848 (м) — высота горы Джомолунгма.
Ответ: 8 848 метров.
Задача от мудрой совы
337. Лимоны одинаковой массы продают поштучно. Масса каждого лимона составляет целое количество граммов. Купили больше двух, но меньше семи лимонов. Масса всей покупки составляет 850 г. Какова масса одного лимона?
Так как купили больше двух, но меньше семи лимонов, то количество купленных лимонов может быть либо 3, либо 4, либо 5, либо 6.
Масса каждого лимона — целое число, причём все лимоны одинаковые. Проверим, на какое из возможных чисел (3, 4, 5 или 6) общая масса покупки 850 г делится без остатка. Для этого применим метод подбора.
Под заданные условия подходит только число 5.
Сколько диагоналей можно провести в девятиугольнике?
Какое количество диагоналей в девятиугольнике?
Не претендую на правильный вопрос. Буду рассуждать. Из каждого угла девятиугольника можно провести шесть диагоналей. Ближайшие углы диагоналями быть не могут, потому как это его стороны. Из следующего угла пять диагоналей. Одна уже есть из предыдущего угла. Затем четыре, три, две и последняя лишь одна.
Вот и получается зависимость 6+5+4+3+2+1= 21 диагональ.
Я делал в уме, геометрию не строил. Потому, если ошибся не судите строго.
Если предположить, что в ответе не дробь, а целое число, то считать вообще ничего не нужно: получается известный «египетский треугольник» с диагональю 5 и катетами 3 и 4. Периметр прямоугольника равен 2(3 + 4) = 14 см. Если не делать такое предположение о целых числах, вычисления тоже будут несложными. Пусть стороны прямоугольника равны а и с. Тогда а2 + с2 = 25, ас = 12, 2ас = 24. Если сложим первое и третье равенства, получим
а2 + 2ас + с2 = 49, (а + с)2 = 49, а + с = ±7 (в зависимости от а > с или а 2 0
Одной диагонали недостаточно, нужна еще одна сторона или отношение сторон. Например, при отношении сторон 1 к 1, то есть квадрате, площадь будет равна половине диагонали в квадрате. Все остальные прямоугольники с такой же диагональю будут иметь меньшую площадь.
ГДЗ учебник по математике 5 класс Бунимович. 19. Многоугольники. Номер №303
ЗАДАЧА−ИССЛЕДОВАНИЕ
Число диагоналей многоугольника можно подсчитать так:
• найти число диагоналей, выходящих из одной вершины, − их на 3 меньше, чем вершин (рисунок справа);
• умножить это число на число вершин;
• разделить результат на 2 (объясните почему).
Сколько диагоналей у семиугольника? десятиугольника? стоугольника? У какого многоугольника 9 диагоналей?
Решение
Десятиугольник:
1 ) 10 − 3 = 7 (диагоналей) − выходит из каждой вершины;
2 ) 7 * 10 = 70 (диагоналей) − удвоенное количество;
3 ) 70 : 2 = 35 (диагоналей) − в десятиугольнике.
Стоугольник:
1 ) 100 − 3 = 97 (диагоналей) − выходит из каждой вершины;
2 ) 97 * 100 = 9700 (диагоналей) − удвоенное количество;
3 ) 9700 : 2 = 4850 (диагоналей) − в стоугольнике.
Пусть a ( вершин) в многоугольнике, тогда:
1 ) a − 3 (диагоналей) − выходит из каждой вершины;
2 ) a(a − 3 ) (диагоналей) − удвоенное количество;
3 ) a(a − 3 ) : 2 = 9 (диагоналей) − в многоугольнике;
a(a − 3 ) = 9 * 2
a(a − 3 ) = 18
18 = 3 * 6 = 9 * 2
Путем подбора можно вычислить, что a = 6, т.к.:
6 * ( 6 − 3 ) = 18
6 * 3 = 18
Значит у шестиугольника 9 диагоналей.
Ответ: 14 диагоналей; 35 диагоналей; 4850 диагоналей; у шестиугольника.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Сколько диагоналей можно провести из одной вершины: пятиугольника
329. 1) Сколько диагоналей можно провести из одной вершины: а) пятиугольника; б) девятиугольника; в) и-угольника, где п > 3?
Ответ
а) Из одной вершины пятиугольника можно провести 2 диагонали.
б) Из одной вершины девятиугольника можно провести 6 диагоналей.
в) Из одной вершины n-угольника можно провести (n-3) диагоналей, так как:
2) Сколько всего диагоналей можно провести: а) в пятиугольнике; б) в девятиугольнике; в) в и-угольнике, где п > 3?
а) Мы знаем, что из одной вершины пятиугольника можно провести 2 диагонали (n-3), Значит из 5 вершин можно провести 5 • 2 = 10 диагоналей (n • (n-3)). Но если провести все 10 диагоналей, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в пятиугольнике можно провести 10 : 2 = 5 диагоналей ((n •(n-3) : 2). Рисунок подтверждает наш вывод.
б) Мы знаем, что из одной вершины девятиугольника можно провести 6 диагоналей (n-3 = 9 — 3 = 6), Значит из 9 вершин можно провести 9 • 6 = 54 диагонали (n • (n-3) = 9 • (9 — 3) = 9 • 6 = 54). Но если провести все 54 диагонали, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в девятиугольнике можно провести 54 : 2 = 27 диагоналей ((n • (n-3) : 2 = 9 • (9 — 3) : 2 = 9 • 6 : 2 = 54 : 2 = 27). Рисунок подтверждает наш вывод.
в) Исследуя предыдущие два задания мы вывели формулу, по которой можно посчитать количество возможных диагоналей в n-угольнике, при n > 3: n • (n-3) : 2. Это значит, у количество диагоналей: