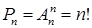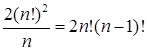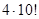сколькими способами можно рассадить 7 человек по 7 местам
Сколькими способами можно рассадить 7 человек в ряд из 7 мест так, чтобы А и Б не оказались соседями?
Денис
7 человек на 7 мест… на первое место претендует 7 человек, на второе-6, на третье-5 и так далее. Эти задания друг от друга не зависят
это будет 7!(семь в факториале) с учетом, что А и Б не окажутся соседями = 7*6*5*4*3*2*1=5040 вариантов
Alexander
Пару и еще 5 человек можно рассадить 6! способами.
пару м енять местами — в 2 р. больше, Итого 2*6! способов
7 человек можно рассадить 7! способами из них 2*6! неправильных
Ответ 7!-6!*2=3600
Маловато что-то…
Олег Никитенко
Количество способов рассадить двоих на 7 мест, если нельзя занимать соседние, равна 7×6 — 12 =30. На каждый способ рассадки А и Б 5! =120 способов рассадить остальных. В итоге, по принципу умножения 30×120=3600 различных способов.
Татьяна Александровна
1) Кол-во способов рассадить 7 чел. на 7 мест равно n = 7!
2) Рассмотрим 6 объектов:
«объект 1» – пара А и Б рассмотрим, как один объект
«объекты 2 – 6» – каждый остальной из оставшихся 5 человек
Кол-во способов рассадить 6 объектов равно 6!
Внутри «объекта 1» — имеется 2 способа рассадить пару А и Б.
Таким образом, кол-во способов рассадить 7 чел. на 7 мест так, чтобы пара А и Б оказались точно рядом равно m = 2 ∙ 6!
3) Тогда кол-во способов рассадить 7 чел. на 7 мест так, чтобы А и Б не оказались рядом равно
N = n — m = 7! – 2 ∙ 6! = 6!∙ (7 – 2) = 3600
Сколькими способами можно рассадить 7 человек по 7 местам?
Сколькими способами можно рассадить 7 человек по 7 местам.
7 человек на 7 мест.
Эти задания друг от друга не зависят(каждый человек может сесть хоть куда) поэтому
(семь в факториале) = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5040 вариантов.
Сколькими способами могут разместиться 6 человек в зрительском зале на 6 свободных мест?
Сколькими способами могут разместиться 6 человек в зрительском зале на 6 свободных мест.
Сколькими способами можно рассадить 5 учеников за круглый стол?
Сколькими способами можно рассадить 5 учеников за круглый стол?
Сколькими способами могут разместиться 5 человек в салоне автобуса на пяти свободных местах?
Сколькими способами могут разместиться 5 человек в салоне автобуса на пяти свободных местах.
Сколькими способами можно рассадить 5 учеников в ряд?
Сколькими способами можно рассадить 5 учеников в ряд?
В автобусе 20 мест, сколькими способами можно рассадить 20 пассажиров в этом автобусе?
В автобусе 20 мест, сколькими способами можно рассадить 20 пассажиров в этом автобусе?
1)Сколькими способами можно рассадить 10 человек на 10 местах в зале?
1)Сколькими способами можно рассадить 10 человек на 10 местах в зале?
2)Сколькими способами можно рассадить 10 человек если имеется 15 свободных мест?
В зале кинотеатра 8 рядов по 16 мест в каждом?
В зале кинотеатра 8 рядов по 16 мест в каждом.
Сколькими способами можно рассадить в этом зале двоих человек так, чтобы они сидели в одном ряду?
Сколькими способами могут разместиться 5 человек в салоне автобуса на пяти свободных местах?
Сколькими способами могут разместиться 5 человек в салоне автобуса на пяти свободных местах?
x∈∅ Точек пересечения нет.
Что то сдесь не то. Может найдёшь ошибку.
Вроде бы, так. Надеюсь, что понятно.
Подробное решение на фотографии.
Решение на фотографии.
Сколькими способами можно рассадить 7 человек по 7 местам
1. Сколько различных пятизначных чисел можно составить из цифр 1, 3, 5, 7, 9 при условии, что ни одна цифра в числе не повторяется?
2. Сколько существует вариантов распределения трех призовых мест, если в розыгрыше участвуют 7 команд?
3. Сколькими способами можно выбрать двух студентов на конференцию, если в группе 33 человека?
4. Решить уравнения
5. Сколько четырехзначных чисел, делящихся на 5, можно составить из цифр 0, 1, 2, 5, 7, если каждое число не должно содержать одинаковых цифр?
6. Из группы в 15 человек должны быть выделены бригадир и 4 члена бригады. Сколькими способами это можно сделать?
7. Буквы азбуки Морзе состоят из символов (точек и тире). Сколько букв можно изобразить, если потребовать, чтобы каждая буква содержала не более пяти символов?
8. Сколькими способами можно составить четырехцветные ленты из семи лент различных цветов.
9. Сколькими способами можно выбрать четырех лиц на четыре различные должности из девяти кандидатов?
10. Сколькими способами можно выбрать 3 из 6 открыток?
11. Перед выпуском группа учащихся в 30 человек обменялась фотокарточками. Сколько всего было роздано фотокарточек.
12. Сколькими способами можно рассадить 10 гостей по десяти местам за праздничным столом?
13. Сколько всего игр должны провести 20 футбольных команд в однокруговом чемпионате?
14. Сколькими способами можно распределить 12 человек по бригадам, если в каждой бригаде по 6 человек?
Теория вероятностей
1. В урне находиться 7 красных и 6 синих шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара красные (событие А)?
2. Девять различных книг расставлены наудачу на одной полке. Найти вероятность того, что четыре определенные книги окажутся поставленными рядом (событие С).
3. Из 10 билетов выигрышными являются 2. Определить вероятность того, что среди взятых наудачу 5 билетов, один выигрышный.
4. из колоды карт (52 карты) наудачу извлекают 3 карты. Найти вероятность того, что это тройка, семерка, туз.
5. Ребенок играет с пятью буквами разрезной азбуки А, К, Р, Ш, Ы. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «Крыша».
6. В ящике находятся 6 белых и 4 красных шара. Наудачу берут два шара. Какова вероятность того, что они окажутся одного цвета?
7. В первой урне находятся 6 черных и 4 белых шара, во второй – 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми?
Случайная величина, математическое ожидание и дисперсия случайной величины
1. Составить закон распределения числа попаданий в цель при шести выстрелах, если вероятность попадания при одном выстреле равна 0,4.
2. Вероятность того, что студент найдет в библиотеке нужную ему книгу, равна 0,3. Составить закон распределения числа библиотек, которые он посетит, если в городе четыре библиотеки.
3. Охотник стреляет по дичи до первого попадания, но успевает делать не более четырех выстрелов. Найти дисперсию числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7.
Сколькими способами можно рассадить 7 человек по 7 местам
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
Пусть первой за стол сядет девочка, рядом с ней есть два места, на каждое из которых может сесть 8 человек, из которых только одна девочка. Таким образом вероятность, что девочки будут сидеть рядом равна
Приведём другое решение (перестановки).
Число способов рассадить 9 человек по девяти стульям равно Благоприятным является случай, когда на «первом» стуле сидит «первая» девочка, на соседнем справа сидит «вторая» девочка, а на остальных семи стульях произвольным образом рассажены мальчики. Поскольку выбрать «первую» девочку можно двумя способами, количество таких исходов равно
А так как «первым» стулом может быть любой из девяти стульев (стулья стоят по кругу), количество благоприятных исходов нужно умножить на 9. Таким образом, вероятность того, что обе девочки будут сидеть рядом, равна
Приведём другое решение (круговые перестановки).
Напомним, что число способов, которыми можно расположить n различных объектов по n расположенным по кругу местам равно (n − 1)! Поэтому посадить за круглым столом 9 детей можно 8! способами. Объединим двух девочек в пару, это можно сделать двумя способами; рассадить по кругу 7 мальчиков и эту неделимую пару можно 7! способами. Тем самым, посадить детей требуемым образом можно 2 · 7! способами, поэтому искомая вероятность равна
Рассуждая аналогично, получим, что в общем случае для n девочек и m мальчиков, сидящих девочки с девочками, а мальчики с мальчиками, количество способов занять места за круговым столом равно n!m!, а вероятность случайной рассадки требуемым образом равна
07. Перестановки
Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.
Перестановками из n элементов называются такие комбинации, каждая из которых содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов.
Поясним это на следующем примере. Из этих трёх элементов: a, b и c. можно составить шесть перестановок: abc, acb, bac, bca, cab, cba. Все приведённые перестановки отличаются друг от друга только порядком их расположения.
Число перестановок n различных элементов обозначают символом Pn и равно
Пример 5.1. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?
Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P6=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P4=4!=24 способами. По принципу умножения имеем
P6P4 = 720×24 = 17280.
Пример 5.2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?
Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равно P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно
4! – 3! = 3×3! = 3×1×2×3 = 18.
Пример 5.3. Сколькими способами можно посадить за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом?
Решение. Естественно предположить, что как мужчины, так и женщины различимы. Предположим также, что места за столом также различимы. Пронумеруем их. Если женщины займут чётные места n! способами, то мужчины будут занимать нечётные места тоже n! способами и наоборот. По правилу умножения получаем 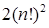
Если места за столом неразличимы, то стол можно поворачивать на одно место, то при этом расположение сидящих не изменится (такая ситуация имеет место, например, на карусели). Поскольку имеется n способов расположения стола относительно сидящих, то предыдущий результат нужно разделить на n.
Вопрос. Сколькими способами можно посадить за круглый стол n супружеских пар, если супруги должны сидеть рядом?
5.1. Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 различных цветов и все стулья должны быть разного цвета.
Ответ: 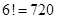
5.2. Дачник выделил на своём участке семь грядок для выращивания овощей, т. к. хочет иметь свои помидоры, огурцы, перец, лук, чеснок, салат и кабачки. Каждый вид должен иметь отдельную грядку. Сколькими способами он может расположить грядки для посадки?
Ответ: 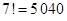
5.3. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находиться в его начале?
Ответ: 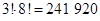
5.4. В первенстве края по футболу участвуют 11 команд. Сколько существует различных способов распределения мест в таблице розыгрыша, если на первое место могут претендовать только 4 определенные команды?
Ответ:
5.5. Сколькими способами можно упорядочить множество <1,2,3,…,2n>так, чтобы каждое чётное число стояло на чётном месте?
Ответ: 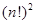
5.6. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?
Ответ: 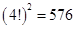
5.7. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?
Ответ: 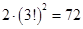
5.8. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.