сколькими способами можно прочитать слово молоко
Сколькими способами можно записать слово молоко?
Сколькими способами можно записать слово молоко?
В кувшине было 12 стаканов молока?
В кувшине было 12 стаканов молока.
На кашу пошло 5 стаканов, а на омлет 2 стакана молока.
Сколько стаканов молока осталось в кувшине?
Как записать условие.
Решить задачу 2 способами карова дала 12 л?
Решить задачу 2 способами карова дала 12 л.
Молока а во второй день 9 литров молока молоко разлили в 3 банки сколько банок наполнилось.
Реши задачи тримя способами?
Реши задачи тримя способами.
В кувшине было 12 стаканов молока.
Сколько стаканов молока осталось в кувшине?
В кувшине 7стаканов молока а в банке 8 стаканов?
В кувшине 7стаканов молока а в банке 8 стаканов.
За обедом дети выпили 5 стаканов молока.
Сколько всего стаканов молока осталось.
Решить задачу разными способами.
В кувшине 7 стаканов молока, а в банке 8 стаканов?
В кувшине 7 стаканов молока, а в банке 8 стаканов.
За обедом дети выпили 5 стаканов молока.
Сколько всего стаканов молока осталось?
Реши задачу разными способами.
Сколько га в 6кв км?
Сколько га в 6кв км.
Записать разными способом.
Как правильно записать условие задачикувшине 7 стаканов молока, а в банке 8 стаканов?
Как правильно записать условие задачикувшине 7 стаканов молока, а в банке 8 стаканов.
За обедом дети выпили 5 стаканов молока.
Сколько всего стаканов молока осталось?
Реши задачу разными способами.
Сколько способами можно записать 47 как число двух простых чисел?
Сколько способами можно записать 47 как число двух простых чисел.
Как решить задачу разными способами : В бидоне 30литров молока, из него налили молоко в банки, в одну 5литров, в другую 3литра?
Как решить задачу разными способами : В бидоне 30литров молока, из него налили молоко в банки, в одну 5литров, в другую 3литра.
Сколько литров молока осталось в бидоне?
Из 200 24 литров молока получают 56 кг творога Сколько килограммов творога можно получить тем же способом из 896 литров молока?
Из 200 24 литров молока получают 56 кг творога Сколько килограммов творога можно получить тем же способом из 896 литров молока.
Лови, это график прямой у = 3х + 6.
4дм 8см1мм = 400мм + 80мм + 1мм = 481мм.
160 раздели на 30. С остатком.
400мм + 80мм + 1мм = 481мм. Ответ : 481мм.
Сколькими способами можно прочитать слово молоко
Сколькими способами можно положить в ряд 2 небесно-голубых лампочки и 4 лампочки цвета травы?
Сколькими способами можно положить в ряд 3 фисташковых лампочки и 5 лампочек цвета морской волны?
Сколькими способами можно переставить буквы слов: а) молоток; б) мисcисипи; в) математика?
б) Перестановку можно выполнить способами;
в) Перестановку можно выполнить способами.
Ответ: а) 840; б) 2 520; в) 151 200.
Сколькими способами можно переставить буквы слов: а) ротор; б) ревербератор; в) синхрофазатрон?
б) Перестановку можно выполнить способами;
в) Перестановку можно выполнить способами.
Ответ: а) 30; б) 3 326 400; в) 5 448 643 200.
Сколькими способами можно переставить буквы слов: а) самовар; б) кофеварка так, чтобы гласные и согласные буквы чередовались?
б) Это можно сделать способами.
Сколькими способами можно переставить буквы слов: а) поворот; б) переворот так, чтобы гласные и согласные буквы чередовались?
б) Это можно сделать способами.
Сколькими способами можно переставить буквы слова математика так, чтобы гласные и согласные буквы чередовались?
Сколькими способами можно переставить буквы слова стереометрия так, чтобы гласные и согласные буквы чередовались?
Сколькими способами можно переставлять буквы в слове перешеек так, чтобы четыре буквы е не шли подряд?
Сколькими способами можно переставлять буквы в слове алабама так, чтобы четыре буквы а не шли подряд?
У папы есть 2 дуриана, 3 фейхоа и 4 рамбутана. В течение 9 дней папа ежедневно даёт сыну по одному фрукту. Сколькими способами можно это делать?
Сколькими способами можно расставить восемь белых фигур (2 ладьи, 2 коня, 2 слона, ферзь и король) на первой линии шахматной доски?
Элементы комбинаторики
Несколько задач по комбинаторике. Общие правила комбинаторики. Комбинаторика в вероятностных задачах.
Просмотр содержимого документа
«Элементы комбинаторики»
Автор –составитель :Паньковская Юлия Вадимовна
Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Начальнику цеха надо распределить несколько видов работ между имеющимися станками, агроному – разместить посевы сельскохозяйственных культур на нескольких полях, заведующему учебной частью школы – составить расписание уроков, ученому-химику – рассмотреть возможные связи между атомами и молекулами, лингвисту – учесть различные варианты значений букв незнакомого языка и т.д. Область математики, в которой изучают закономерности создания подобных комбинаций, называется комбинаторикой.
Комбинаторика возникла в XVI веке. В то время в жизни общества большое место занимали азартные игры. В карты и кости выигрывались и проигрывались золото и бриллианты, дворцы и имения, породистые кони и дорогие украшения. Широко были распространены всевозможные лотереи. Понятно, что первоначально комбинаторные задачи касались в основном азартных игр – вопросов, насколько часто можно выбросить данное число очков, бросая две или три кости, или получить двух королей в данной карточной игре. Эти и другие проблемы азартных игр явились движущей силой в развитии комбинаторики и теории вероятностей.
Большим подспорьем для математиков являлось то, что решения задач такого рода можно было проверить на практике – во время игр. Зачастую проходило так, что во время многочасовых игр замечались определенные закономерности (например, что определенные комбинации карт или костей появляются чаще других), о которых игроки сообщали математикам, а последние объясняли эти наблюдения.
Положение резко изменилось после появления во второй половине ХХ века электронных вычислительных машин и связанного с этим расцветом дискретной математики. С этого момента комбинаторика переживает период бурного развития. Комбинаторные методы находят множество применений. Они используются для решения транспортных задач (в частности задач по составлению расписаний), для составления планов производства и реализации продукции, в теории случайных процессов, статистике, вычислительной математике, планировании экспериментов, шахматных программах для ЭВМ и т.д. Комбинаторика используется для составления и декодирования шифров и для решения других проблем теории кодирования и теории информации. Значительную роль комбинаторные методы играют и в чисто математических вопросах – при изучении конечных геометрий, теории групп и их представлений, неассоциативных алгебр и т.д.
ОБЩИЕ ПРАВИЛА КОМБИНАТОРИКИ
Попробуем помочь председателю. Нам нужно решить такую комбинаторную задачу: сколько трехзначных номеров, не содержащих цифры 8?
Для решения этой задачи определим сначала, сколько однозначных номеров не содержит цифру 8. Ясно, что таких номеров девять: 0, 1, 2, 3, 4, 5, 6, 7, 9. А теперь найдем все двузначные номера, не содержащие цифру 8. Их можно составить так: взять любой из найденных однозначных номеров и написать после него любую из девяти допустимых цифр. В результате из каждого однозначного номера получится девять двузначных. А так как однозначных номеров тоже девять, то получиться 9·9=9 2 двузначных номеров без цифры 8.
За каждым из них снова можно поставить любую из девяти допустимых цифр. В результате получим 9 2 ·9=9 3 =729 трехзначных номеров, не содержащих цифру 8. Значит, таких членских билетов хватит на 729 членов клуба.
А если взять не трехзначные, а четырехзначные номера, то номеров, не содержащих цифру 8, будет 9 4 =6561, а пятизначных – 9 5 =59049.
Заместитель председателя был еще суевернее. Так как число 0 похоже на вытянутое колесо, он предложил отказаться и от этой цифры и попробовать обойтись восемью цифрами: 1, 2, 3, 4, 5, 6, 7, 9. А это у него получится, потому что эта задача похоже на решенную выше, только вместо девяти цифр у нас всего восемь. Поэтому и в ответе надо заменить 9 на 8, так что трехзначных номеров билетов, не использующих цифры 0 и 8, существует 8 3 =512, а членов клуба почти 600.
Зоя Петровна и ее дочь Нина часто играли в лото. Каждая брала по три карточки, Нина хорошо перемешивала бочонки в мешке, затем доставала из мешка очередной бочонок с числом (от 1 до 90), называла его, и тот, у кого на карточке обнаруживалось это число, закрывал его бочонком.
Играли они часто, помнили, как начинались многие игры (кто первым и какой брал себе бочонок), уже не раз первым попадался один и тот же бочонок, но первые два бочонка каждый раз извлекались другие. И однажды Нина задумалась – много ли способов извлечь один за другим два бочонка из мешка, если в нем 90 бочонков?
Первый можно извлечь 90 способами – это понятно, а дальше? Ведь если бочонок 28 уже извлечен, то второй раз его извлечь нельзя. Но Нина как раз в это день готовила таблицу первенства школы по баскетболу, в которой клетки по диагонали перечеркивались (ведь играть сама с собой команда не может), и сообразила, что тот же метод годится и здесь. Она представила себе таблицу 90
Тогда каждая клетка задает один вариант выбора двух бочонков, вот только клетки диагонали надо зачеркнуть (дважды один бочонок извлечь нельзя).
В этой таблице 90·90=8100 клеток 90 зачеркнуты, значит, остается 8010 вариантов. Это и есть число способов извлечь один за другим два бочонка из 90.
А затем Нина сообразила, что можно рассуждать иначе. Первый бочонок можно извлечь 90 способами. После этого в мешке останется 89 бочонков, правда, каких – зависит от того, какой бочонок извлечен первым. Но способов извлечь второй бочонок всегда будет 89 для каждого из 90 способов извлечь первый бочонок, а всего способов будет 90·89=8010.
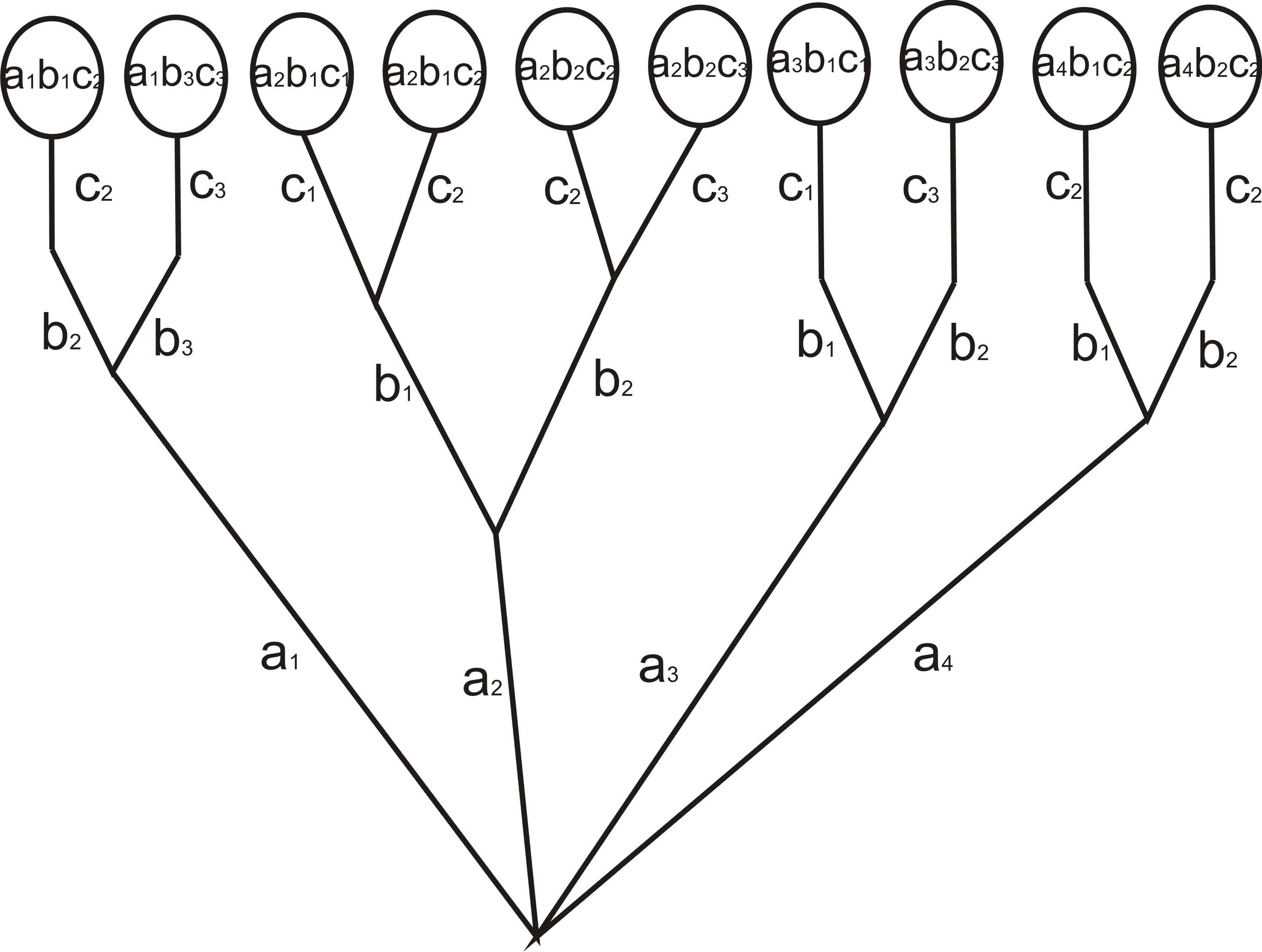
«Команда космического корабля»
В случае, когда число возможных выборов на каждом шагу сложным образом зависит от того, какие элементы были выбраны ранее, удобно изображать процесс составления комбинаций в виде «дерева». Сначала из данной точки проводят столько отрезков, сколько различных выборов можно сделать на первом шагу (таким образом, каждый отрезок соответствует одному элементу). Из конца каждого отрезка проводят столько отрезков, сколько можно сделать выборов на втором шагу, если в первый раз был выбран данный элемент, и т.д.
В результате такого построения получатся «дерево», рассмотрение которого дает число решений нашей задачи.
Рассмотрим следующий пример. Известно, что при составлении команд многоместных космических кораблей возникает вопрос о психологической совместимости участников космического путешествия. Даже вполне подходящие порознь люди могут оказаться непригодными для длительного совместного путешествия. Предположим, что надо составить команду космического корабля из трех человек: командира, инженера и врача. На место командира есть четыре кандидата: а1, а2, а3, а4; на место инженера – 3 кандидата: b1, b2, b3 и на место врача – тоже 3 кандидата: с1, с2, с3. Проведенная проверка показала, что командир а1 психологически совместим с инженерами b1 и b3 и врачами с2 и с3; командир а2 – с инженерами b1 и b2 и всеми врачами; командир а3 – с инженерами b1 и b2 и врачами с1, с3; командир а4 – со всеми инженерами и врачом с2. Кроме того, инженер b1 психологически несовместим с врачом с3, инженер b2 – с врачом с1 и инженер b3 – с врачом с2. Сколькими способами при этих условиях может быть составлена команда корабля?
Соответствующее дерево изображено на рис.1.
Оно показывает, что есть лишь 10 допустимых комбинаций. При этом после каждого выбора командира аi у нас есть 2 варианта выбора инженера bj, поэтому появляется 8 пар командир-инженер, а дальше для каждой такой пары в 6 случаях врач ck определен единственным образом (в силу требований совместимости), а в 2 случаях есть выбор из двух врачей.
Задача 1. Крыса бежит по лабиринту, который устроен так, что сначала она должна выбрать одну из двух дверей, затем одну из трех дверей, а за каждой из них ее ожидают четыре двери. Пройдя какую-либо дверь, крыса не может вернуться через нее обратно. Сколькими различными путями крыса может пройти лабиринт?
Задача 2. Сколькими способами можно прочитать слово КРОНА в таблице, начиная с буквы К в левом верхнем углу и двигаясь вправо или вниз до последней буквы?
КОМБИНАТОРИКА
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m (

Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Алгебра
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Комбинаторика и ее основные принципы
Очень часто приходится решать задачи, в которых надо посчитать количество возможных вариантов для той или иной ситуации. Например, сколько позиций может возникнуть на шахматной доске после первого хода обоих игроков? Сколько разных паролей длиною в десять символов можно записать, если ни один символ не использовать дважды? Сколько разнообразных комбинаций чисел может выпасть при игре в лотерею «6 из 49»? На все эти вопросы помогает ответить специальный раздел математики, называемый комбинаторикой. Почти всегда комбинаторную задачу можно сформулировать так, чтобы ее вопрос начинался словами «сколькими способами…».
Очевидно, что если в конечном множестве содержится n элементов, то есть ровно n способов выбрать один из них.
Пример. В классе 15 человек. Сколькими способами учитель может назначить одного из них ответственным за чистоту доски?
Ответ. Таких способов ровно 15.
В комбинаторике существует два основных правила. Первое из них называется правилом сложения.
Несмотря на формулировку, по сути это очень простое правило.
Пример. В магазине продается 14 телевизоров Panasonic и 17 телевизоров Sony. Петя хочет купить один телевизор. Сколько у него вариантов покупки?
Решение. По правилу сложения Петя может выбрать один из 14 + 17 = 31 телевизоров.
Ответ: 31 телевизор.
Особое значение имеет второе правило, которое называют правилом умножения.
Проиллюстрируем это правило.
Пример. В секции бадминтона 15 мальчиков и 20 девочек. Тренер должен отправить на соревнования смешанную пару. Сколько вариантов действий у него?
Решение. Тренер может составить 15•20= 300 разнополых пар из своих воспитанников.
Пример. Пете нужно купить технику для компьютера. В магазине продается 20 различных клавиатур, 25 моделей геймпадов и 30 компьютерных мышей. Купить надо по одному экземпляру каждого из этих устройств. Сколько вариантов покупки есть у него?
Решение. Сначала подсчитаем число возможных пар «клавиатура-геймпад». Их количество равно 20•25 = 500. Теперь составим «тройку» из одной из 500 пар и одной из 30 мышей. Число троек равно 500•30 = 15000.
Правила сложения и умножения можно комбинировать.
Пример. Сколько слов не более чем из трех букв можно составить, используя алфавит, содержащий ровно 30 букв?
Решение. Очевидно, что слов из одной буквы можно составить ровно 30. Количество двухбуквенных слов равно количеству пар, которые можно составить из этих букв, то есть 30•30 = 900. Трехбуквенных слов можно составить 30•30•30 = 27000. Всего же слов длиною не более 3 букв будет
30 + 900 + 27000 = 27930
Далее мы изучим основные понятия комбинаторики – перестановки, размещения, сочетания.
Перестановки
Рассмотрим простейшую комбинаторную задачу. На полке расставляют по порядку книги. Их ставят вертикально друг за другом. Сколькими способами можно расставить на полке 2 книги? Очевидно, что двумя:
Либо синяя книжка будет первой слева, либо она будет находиться в конце полки, третьего варианта здесь нет. Здесь условно считается, что варианты, когда между книгами есть зазоры, идентичны вариантам без зазоров:
То есть нас интересует исключительно порядок, в котором стоят книги. Каждый из найденных вариантов называется перестановкой книг. Перестановкой называют любое конечное множество, для элементов которого указан порядок элементов.В комбинаторике перестановки являются одними из основных объектов изучения.
Например, если в забеге на 100 метров стартует 8 спортсменов, то они образуют множество участников забега. После финиша становится известно, кто занял 1-ое место, кто оказался вторым или третьим, а кто стал последним. Результат забега будет перестановкой, ведь он представляет собой список спортсменов с указанием их мест, то есть он определяет порядок между ними.
Вернемся к примеру с книгами. Обозначим количество возможных перестановок n элементов как Рn. Две книжки можно расставить двумя разными способами, поэтому Р2 = 2. Обозначим эти перестановки как АБ и БА. Сколько способов расстановки есть в случае трех книжек? Их все можно получить из вариантов с 2 книжками, добавляя между ними книгами ещё один том:
Видно, что между 2 книгами есть три позиции, на которые можно поставить 3-ий том. Общее количество вариантов равно произведению числа этих позиций и количества вариантов для 2 книг, то есть Р3 = 3•Р2 = 3•2 = 6:
Итак, мы имеем 6 перестановок для 3 книг:
А сколько перестановок существует для 4 книг? Снова-таки, между тремя книгами 4-ый том можно поставить четырьмя способами:
То есть из перестановки трех книг АБВ можно получить 4 перестановки:
Всего существует 6 перестановок для 3 книг (Р3 = 6), и для каждой из них можно построить 4 перестановки из 4 книг. Получается, что общее количество перестановок 4 книг равно
Продолжая подобные рассуждения, можно убедиться, что количество перестановок 5 предметов в 5 раз больше, чем перестановок для 4 объектов:
И вообще, если число перестановок n объектов равно Рn, то количество перестановок (n + 1)объекта равно в (n + 1)раз больше:
При этом отметим, что 1 книгу можно расставить на полке только одним способом:
То есть Р1 = 1. Теперь выпишем значения чисел Р при разном количестве переставляемых предметов, используя формулуРn+1 = (n + 1)Рn
Видно, что количество перестановок n объектов равно произведению всех натуральных чисел от 1 до n. В математике есть специальная функция для вычисления значения этого произведения. Она называется факториалом и обозначается восклицательным знаком.
Например, факториал 6 вычисляется так:
Мы убедились на примере с книгами, что количество перестановок из n различных объектов, которое обозначается как Рn, равно n!.
Относительно факториала надо заметить несколько важных моментов. Во-первых, очевидно, что факториал единицы равен 1:
Во-вторых, иногда в комбинаторных задачах приходится вычислять факториал нуля. По ряду соображений эта величина также принимается равной единице
Объяснить это можно так. Факториал числа можно представить как произведение этого числа и факториала предыдущего числа, например:
5! = 1•2•3•4•5 = (1•2•3•4)•5 = 4!•5
7! = 1•2•3•4•5•6•7 = (1•2•3•4•5•6)•7 = 6!•7
В общем случае формула выглядит так:
Из неё несложно получить, что
Подставив в эту формулу единицу, получим
Пример. Сколькими способами тренер может расставить 4 участников эстафеты 4х400 м по этапам эстафеты?
Решение. Количество таких способов равно числу перестановок 4 различных объектов Р4:
Пример. Вася решил изучать сразу 7 иностранных языков, причем на занятия по каждому из них он собирается выделить ровно один день в неделе. Сколько вариантов расписаний занятий может составить себе Вася?
Решение. В данном случае расписание занятий – это порядок, в котором Вася в течение недели будет изучать иностранные языки, например:
Такое расписание можно описать последовательностью символов:
Создавая расписание, Вася переставляет 7 языков, поэтому общее количество расписаний равно 7!:
Пример. Сколько пятизначных цифр можно записать, используя цифры 0, 1, 2, 3, 4, причем каждую не более одного раза?
Решение. Общее количество перестановок 5 цифр составляет Р5. Однако нельзя начинать запись числа с нуля. Так как, перестановка 12340 – это пятизначное число (двенадцать тысяч триста сорок), а перестановка 03241 – не является пятизначным числом.
Расстановок, начинающихся с нуля, ровно Р4, поэтому общее количество допустимых цифр равно Р5 – Р4:
Р5 – Р4 = 5! – 4! = 120 – 24 = 96
Пример. На полке расставляют 7 книг, однако 3 из них образуют трехтомник. Тома трехтомника должны стоять друг за другом и в определенном порядке. Сколько существует способов расстановки книг?
Решение. Будем считать трехтомник одной книгой. Тогда нам надо расставить 5 книг
Пример. Необходимо расставить 7 книг на полке, но три из них принадлежат одному автору. Их надо поставить друг с другом, но они могут стоять в любом порядке. Сколько возможно перестановок книг.
Решение. Снова будем считать три книги как один трехтомник. Получается, что существует 5! = 120 вариантов. Однако каждому из них соответствует 3! = 6 расстановок книг внутри трехтомника, например:
В итоге на каждую из 120 расстановок приходится 6 вариантов расстановки трехтомника, а общее число расстановок равно, согласно правилу умножения, произведению этих чисел:
Перестановки с повторениями
До этого мы рассматривали случаи, когда все переставляемые объекты были различными. Однако порою некоторые из них не отличаются друг от друга. Пусть на полке надо расставить 3 книги, но две из них одинаковые. Сколько тогда существует перестановок? Общее число перестановок 3 книг составляет 3! = 6:
Здесь одинаковые книги отмечены как А и А1. Очевидно, что 1-ый и 2-ой варианты (А1АБ) и (АА1Б) на самом деле не отличаются друг от друга. В них отличается лишь порядок одинаковых книг А и А1. В первом случае за А1 следует А, а во втором, наоборот, за А следует А1. Тоже самое можно сказать про варианты 3 и 4, 5 и 6. Получается, что все возможные перестановки можно разбить на группы, в которых находятся «перестановки-дубликаты»:
В каждой группе находится ровно по два «дубликата». Почему именно по два? Это число равно количеству перестановок одинаковых книг. Так как одинаковых томов 2, а Р2 = 2, то в каждой группе по 2 «дубликата». Действительно, если бы мы «убрали» с полки все книги, кроме повторяющихся, то там осталось бы только 2 одинаковых тома, которые можно переставить двумя способами.
Для того чтобы найти количество «оригинальных» перестановок, надо их общее количество поделить на число дубликатов в каждой группе.
Пусть теперь надо расставить 4 книги, из которых 3 одинаковы. Обозначим тома как А, А1, А2 и Б. Всего можно записать 4! = 24 перестановки. Однако каждые 6 из них будут дублировать друг друга. То есть их можно разбить на группы, в каждой из которых будет 6 идентичных «дубликатов»:
1-ая группа: БАА1А2, БАА2А1, БА1АА2, БА1А2А, БА2АА1, БА2А1А
2-ая группа: АБА1А2, АБА2А1, А1БАА2, А1БА2А, А2БАА1, А2БА1А
3-ая группа: АА1БА2, АА2БА1, А1АБА2, А1А2БА, А2АБА1, А2А1БА
4-ая группа: АА1А2Б, АА2А1Б, А1АА2Б, А1А2АБ, А2АА1Б, А2А1АБ
И снова для подсчета числа оригинальных перестановок надо из общее число расстановок поделить на количество дубликатов в каждой группе:
Для обозначения перестановок с повторениями используется запись
где n – общее количество объектов, а n1, n2, n3,… nk – количество одинаковых элементов. Например, в задаче с 4 книгами мы искали величину Р4(3, 1), потому что всего книг было 4, но они были разбиты на две группы, в одной из которых находилось 3 одинаковых тома (буквы А, А1, А2), а ещё одна книга (Б) составляла вторую группу. Мы заметили, что для вычисления числа перестановок с повторениями надо общее число перестановок делить на количество дублирующих перестановок. Формула в общем случае выглядит так:
Пример. Вася решил, что ему стоит изучать только два иностранных языка. Он решил 4 дня в неделю тратить на английский, а оставшиеся три дня – на испанский. Сколько расписаний занятий он может себе составить.
Решение. Вася должен расставить 3 урока испанского и 4 урока английского, тогда n1 = 3, а n2 = 4. Общее количество уроков равно 3 + 4 = 7. Тогда
Обратите внимание, что для удобства при делении факториалов мы не вычисляли их сразу, а пытались сократить множители. Так как в ответе любой комбинаторной задачи получается целое число, то весь знаменатель дроби обязательно сократится с какими-нибудь множителями в числителе.
Пример. У мамы есть 3 яблока, 2 банана и 1 апельсин. Эти фрукты она распределяет между 6 детьми. Сколькими способами она может это сделать, если каждый должен получить по фрукту?
Решение. Всего есть три группы фруктов. В первой находится 3 яблока, поэтому n1 = 3. Во второй группе 2 банана, поэтому n2 = 2. В третьей группе только 1 апельсин, поэтому nk = 1. Общее число фруктов равно 6. Используем формулу:
В знаменателе формулы для перестановок с повторениями мы записываем число объектов в каждой группе одинаковых предметов. Так, если переставляются 3 яблока, 2 банана и 1 апельсин, то в знаменателе мы пишем 3!•2!•1!. Но что будет, если в каждой группе будет находиться ровно один уникальный объект? Тогда мы запишем в знаменателе произведение единиц:
В итоге мы получили ту же формулу, что и для перестановок без повторов. Другими словами, перестановки без повтора могут рассматриваться просто как частный случай перестановок с повторами.
Размещения
Пусть в футбольном турнире участвуют 6 команд. Нам предлагают угадать те команды, которые займут призовые места (то есть первые три места). Сколько вариантов таких троек существует?
Сначала запишем ту команду, которая выиграет турнир. Здесь есть шесть вариантов, по количеству участвующих команд. Запишем эти варианты:
Далее выберем один из вариантов и для него укажем серебряного призера соревнований. Здесь есть только 5 вариантов, ведь 1 из 6 команд уже записана на 1-ом месте:
Такую пятерку можно записать для каждого из шести вариантов того, кто станет чемпионом. Получается, что всего есть 6•5 = 30 пар «чемпион – серебряный призер». Наконец, для одной такой пары можно записать 4 варианта того, кто окажется третьим (две команды писать нельзя, так как они уже записаны на первых двух строчках):
Для каждой пары можно записать 4 тройки призеров. Так как число пар «чемпион – вице-чемпион» равно 6•5 = 30, то число троек составит 6•5•4 = 120.
В данном случае из некоторого множества команд мы выбрали несколько и расположили их в каком-то порядке. То есть мы выбрали упорядоченное множество. В комбинаторике оно называется размещением.
Если общее число команд обозначить как n (в этом примере n = 6), а количество упорядочиваемых команд равно k, то количество таких размещений в комбинаторике обозначается как
В примере с командами количество размещений равнялось 120:
Читается эта запись как «число размещений из 6 по 3 равно 120».
Для нахождения этого числа мы перемножили k (3)множителей. Первый из них был равен n(6), так как каждая из n команд могла занять первая место. Второй множитель был равен (n– 1), так как после определения чемпиона мы могли поставить на вторую позицию одну из (n– 1) команд. Третий множитель был равен (n– 2). По этой логике каждый следующий множитель будет меньше предыдущего на единицу. Например, чтобы вычислить число размещений из 7 по 4, надо перемножить 4 множителя, первый из которых равен 7, а каждый следующий меньше на 1:
Однако математически удобнее представлять это произведение как отношение двух факториалов. Для этого умножим количество размещений на дробь 3!/3!, равную единице. Естественно, число размещений из-за умножения на единицу не меняется:
Число 3 в данном случае можно получить, если из 7 вычесть 4. В общем случае из числа n надо вычесть число k. Тогда формула для вычисления количества размещений примет вид:
Пример. В программе 8 «А» класса 12 различных предметов. В понедельник проводится 5 занятий подряд. Сколько существует вариантов расписаний для класса, если в течение понедельника нельзя проводить два одинаковых урока?
Решение. Для составления расписания нужно выбрать 5 предметов и расставить их по порядку. Поэтому нам необходимо найти размещение из 12 по 5:
Пример. В вагоне 10 свободных мест. В него зашло 6 пассажиров. Сколькими способами они могут расположиться в вагоне?
Решение. Из десяти мест надо выбрать шесть и указать для каждого, какому пассажиру оно соответствует. То есть каждый вариант рассадки пассажиров – это размещение из 10 по 6. Найдем их количество:
Заметим, что перестановка – это частный случай размещения, когда k = n. Действительно, если нам надо указать тройку призеров турнира, в котором участвуют 6 команд, то мы указываем размещение из 6 по 3. Но если мы указываем для каждой из 6 команд, какое место она займет в чемпионате, то это размещение из 6 по 6. С другой стороны, это расстановка одновременно является и перестановкой 6 команд. Убедимся, что в этом частном случае формула для подсчета количества размещений покажет тот же результат, что и формула для перестановок
Для примера с 6 командами это будет выглядеть так:
Здесь мы использовали тот факт, что факториал нуля принимается равным единице. Данное рассуждение можно, наоборот, использовать для того, чтобы доказать, что факториал нуля – это единица.
Сочетания
Выбирая размещение, мы должны были выбрать из множества несколько объектов и упорядочить их. В частности, мы выбирали три команды из шести и указывали, какая из них будет первой, какая второй, а какая третьей. Поэтому размещения «Локомотив, Зенит, Краснодар» и «Локомотив, Краснодар, Зенит» отличались друг от друга.
Однако порою этот порядок не имеет значения. Так, существует известная лотерея, где предлагается угадать 7 чисел из 49, которые выпадут во время розыгрыша из барабана. При этом порядок их выпадения не играет никакой роли. Игрок, выбирая эти 7 чисел, с точки зрения математики формирует сочетание из 49 по 7.
Количество возможных сочетаний из n по k обозначается буквой С:
Для вычисления количеств сочетаний из n по k сначала найдем количество аналогичных размещений. Оно вычисляется по формуле:
Однако все они соответствуют только одному сочетании – ЛКЗ. Таким образом, считая количество размещений, мы посчитали каждое сочетание не один, а 3! раз. Поэтому для нахождения количества сочетаний в комбинаторике надо поделить число размещений на число перестановок k элементов:
Эта формула связывает важнейшие понятия комбинаторики – перестановки, сочетания и размещения. Подставим в неё формулы для размещений и перестановок и получим:
Пример. Сколько троек призеров турнира можно составить, выбирая три футбольные команды из шести?
Решение. Посчитаем число сочетаний из 6 по 3:
Пример. Сколько комбинаций чисел может составить игрок, играющий в лотереи «5 из 36», «6 из 45», «7 из 49»?
Решение. В каждом из этих случаев игрок выбирает сочетание нескольких чисел. Посчитаем их число:
Ответ: 376992; 8145060; 85900584
Пример. На плоскости отмечены 8 точек, причем никакие три из них не лежат на одной прямой. Сколько различных прямых можно провести через них? Сколько треугольников и четырехугольников можно построить с вершинами в этих точках?
Решение. Для того чтобы провести прямую, достаточно выбрать любые 2 точки из 8. Общее количество прямых будет равно числу сочетаний из 8 по 2:
Заметим принципиальную важность того условия, что никакие три точки не лежат на одной прямой. Оно гарантирует, что при выборе двух различных точек мы будем получать различные прямые. Если бы, например, точки АВС лежали бы на одной прямой, то при выборе сочетаний АВ, ВС и АС мы получали бы одну и ту же прямую:
Это же условие гарантирует, что, выбрав любые 3 и 8 точек, мы сможем построить треугольник с вершинами в этих точках, а выбрав 4 точки, получим четырехугольник. Поэтому для подсчета количества треугольников и четырехугольников следует искать число сочетаний по 3 и 4:
Ответ: 28 прямых, 56 треугольников и 70 четырехугольников.
Пример. В одной урне находится 10 различных шаров с номерами от 0 до 9, а в другой – 8 различных шаров с первыми восемью буквами алфавита. По условиям лотереи ведущий вытаскивает из первой урны два шара с числами, а из второй – три шара с буквами. Для победы в лотерее надо угадать выпавшие шары. Сколько комбинаций шаров может выпасть в игре?
Решение. Посчитаем отдельно, сколькими способами можно выбрать 2 шара с цифрами из 10 и 3 шара с буквами из 8:
По правилу умножения мы должны перемножить эти числа, чтобы найти общее количество возможных вариантов:
Заметим, что выбирая, например, сочетание из 49 по 7, мы одновременно выбираем и сочетание из 49 по 49 – 7 = 42. Действительно, игрок, обводящий в кружок в лотерейном билете свои 7 счастливых чисел, одновременно и определяет остальные 42 числа, какие числа он НЕ считает счастливыми. Для наглядности запишем число сочетаний в обоих случаях:
Получили одну и ту же дробь, в которой отличается лишь последовательность множителей в знаменателе. Можно показать, что и в общем случае число сочетаний из n по k совпадает с количеством сочетаний из n по (n– k):


















