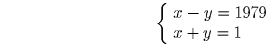сколькими способами можно представить 202 в виде разности квадратов двух натуральных чисел
20 БАЛЛОВ Сколькими способами можно представить 202 в виде разности квадратов двух натуральных чисел?
20 БАЛЛОВ Сколькими способами можно представить 202 в виде разности квадратов двух натуральных чисел?
Чтобы получилось произведение 202 множители должны быть равны (202 и1) или (101 и 2)
Получим 2 системы уравнений
Решая эти системы получим
Ответ нет таких натуральных чисел.
Сколькими способами число 100 можно представить в виде суммы нескольких последовательных натуральных чисел?
Сколькими способами число 100 можно представить в виде суммы нескольких последовательных натуральных чисел?
Выберите верное утверждение 1?
Выберите верное утверждение 1.
Простое число можно представить в виде суммы двух чётных натуральных чисел.
2. простое число можно представить в виде суммы двух нечётных натуральных чисел.
То Число m можно представить в виде суммы квадратов двух целых чисел.
Разность квадратов двух натуральных чисел равна 64, а разность самих чисел равна 2?
Разность квадратов двух натуральных чисел равна 64, а разность самих чисел равна 2.
Можно ли 1998 представить в виде разности двух квадратов?
Можно ли 1998 представить в виде разности двух квадратов.
Разность квадратов двух натуральных чисел равна 64, а разность самих чисел равна 2?
Разность квадратов двух натуральных чисел равна 64, а разность самих чисел равна 2.
Разность квадрата двух натуральных чисел равна 13, а сумма этих чисел равна 13?
Разность квадрата двух натуральных чисел равна 13, а сумма этих чисел равна 13.
Представь число120в виде произведения двух натуральных чисел, одно из которых на26меньше другого?
Представь число120в виде произведения двух натуральных чисел, одно из которых на26меньше другого.
Сумма квадратов двух последовательных натуральных чисел равна 545?
Сумма квадратов двух последовательных натуральных чисел равна 545.
Чему равна разность квадратов этих чисел?
Сколькими способами можно представить 202 в виде разности квадратов двух натуральных чисел
Задача 1: (6–8) Сколькими способами число 1979 можно представить в виде разности двух квадратов натуральных чисел?
Решение: Пусть 1979 = x² – y² — представление, описанное в условии. Тогда 1979 = (x – y)(x + y). Поскольку 1979 — число простое, то существует единственное его представление в виде произведения двух натуральных чисел 1979 = 1 1979. Поэтому должны выполняться либо равенства
Первая система положительных решений не имеет, а единственным решением второй системы будет x = 990, y = 989. Значит, представление числа 1979 в виде разности квадратов двух натуральных чисел единственно. См. Т9.
Задача 2: (6–8) В соревнованиях участвуют 10 фигуристов. Соревнования судят трое судей следующим способом: каждый судья по-своему распределяет между фигуристами места (с первого по десятое), после чего победителем считается фигурист с наименьшей суммой мест. Какое наибольшее значение может принимать эта сумма у победителя (победитель единственный)?
Решение: Докажем, что искомое наибольшее значение суммы мест победителя равно 15. Для этого необходимо доказать два утверждения. Первое: при любом варианте судейства сумма мест победителя не может быть больше 15. Второе: существует такой вариант судейства, при котором сумма мест победителя равна 15.
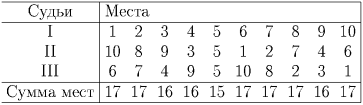
Для доказательства второго утверждения достаточно привести пример судейства, при котором сумма мест победителя равна 15. Такой пример приведен ниже в виде таблицы:
Задача 3: (6–8) В колоде 16 карт, пронумерованных сверху вниз. Разрешается снять часть колоды сверху, после чего снятую и оставшуюся части колоды, не переворачивая «врезать» друг в друга. Может ли случиться, что после нескольких таких операций карты окажутся пронумерованными снизу вверх? Если да, то за какое наименьшее число операций это может произойти?
Решение: Простейший способ осуществить требуемую перестановку — брать карты сверху по одной (это допускается условием задачи) от первой до пятнадцатой и класть на соответствующее место: первую — в самый низ, каждую следующую — между шестнадцатой и предыдущей из положенных карт. Достаточно ясно, что такой способ перестановки за 15 операций не является оптимальным.
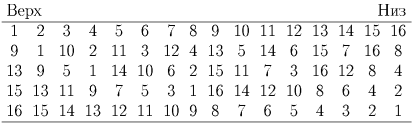
Приведем более «хитрый» способ, позволяющий добиться того же результата всего за 4 операции. Каждый раз будем снимать ровно половину колоды — 8 карт сверху и «врезать» снятую часть колоды в оставшуюся «через одну». Трансформация колоды при таких операциях показана на схеме:
Эти преобразования можно описать проще (подумайте как), если пронумеровать карты числами от 0 до 15 в двоичной системе счисления.
Докажем теперь, что приведенный способ оптимален, т.е. что за три операции такую перестановку осуществить невозможно. Рассмотрим произвольные три операции над колодой, удовлетворяющие условию задачи. При каждой операции колода делится на две части: часть, которая снимается, и часть, которая остается. Поскольку всего карт 16, то одна из этих частей содержит не менее восьми карт. Аналогичное рассуждение показывает, что среди этих карт найдутся по крайней мере четыре, которые при второй операции либо все были в снятой части колоды, либо все в оставшейся. А среди них, в свою очередь, найдутся две карты, оказавшиеся в одной части и при третьей операции. Таким образом, мы нашли две карты, которые при всех операциях либо снимались, либо оставались в колоде вместе. Тем самым порядок этих карт в колоде после трех операций не изменился. Значит, не могло получиться так, что нумерация карт в колоде поменялась на противоположную.
Сколькими способами можно представить 202 в виде разности квадратов двух натуральных чисел
Напрашивается вопрос, какие простые числа и сколькими способами могут быть представлены в виде разности двух квадратов натуральных чисел.
Предположим, что простое число 
разлагается на разность двух квадратов натуральных чисел: 
где х и у — натуральные числа, причем, очевидно, 
Отсюда 
значит, 
у являются натуральными делителями числа 
причем первый меньше второго. Но так как 
простое число, то 
следовательно, 
. Таким образом, число 
должно быть нечетным, и в этом случае мы имеем единственное разложение
Теорема 19. Каждое нечетное простое число представимо в виде разности двух квадратов натуральных чисел и притом только одним способом.
Легко доказать, что для того чтобы натуральное число 
было разностью двух квадратов натуральных чисел, необходимо и достаточно, чтобы при делении на 4 оно не давало в остатке 2.
Можно доказать, что существуют числа, допускающие достаточно большое число разложений на разность двух квадратов. Из теоремы 19 следует, что натуральное число, допускающее более чем одно разложение на разность двух квадратов натуральных чисел, не является простым.
Впрочем, легко также доказать, что если нечетное число имеет только одно разложение на разность двух квадратов целых чисел, то оно является простым. В самом деле, предположим, что нечетное число
составное и, значит, 
где а и 
натуральные числа 
Очевидно, имеем
причем если, например, 
то 
(так как 
), и, следовательно, наши разложения являются различными.
Таким образом, нечетное составное число дает по крайней мере два различных разложения на разность двух квадратов целых чисел. Заметим, однако, что имеются нечетные составные числа, представимые единственным способом в виде разности двух квадратов натуральных чисел, например число 9. (Можно доказать, что такими числами являются квадраты простых нечетных чисел.)
Перейдем теперь к вопросу о разложении простых чисел на суммы трех квадратов натуральных чисел.