сколькими способами можно переставить буквы слова девушка так чтобы гласные шли в алфавитном порядке

Сколькими способами можно переставить буквы слова девушка так чтобы гласные шли в алфавитном порядке

Задача 1:

Из класса, в котором учатся 30 человек, нужно выбрать двоих школьников для участия в математической олимпиаде. Сколькими способами это можно сделать?

Решение:

Первого ученика можно выбрать 30 способами, второго, независимо от выбора первого ученика, – 29 способами. При этом каждая пара учитывается дважды. Поэтому ответ: 30 • 29/2 = 435 способов.

Задача 2:

Сколькими способами можно выбрать команду из трех школьников в классе, в котором учатся 30 человек?

Решение:

Первого ученика можно выбрать 30 способами, второго – 29 способами, третьего – 28 способами. Таким образом получаем 30 • 29 • 28 вариантов выбора. Однако каждая команда при этом подсчете учтена несколько раз: одна и та же тройка учеников может быть выбрана по разному, например, сначала А, потом В, потом С или сначала С, потом А, потом В и т.д. Поскольку число перестановок из трех элементов равно 3!, то каждая команда учтена нами ровно 3! = 6 раз. Поэтому 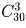равно (30 • 29 • 28)/3!.

Задача 3:

Сколькими способами можно выбрать 4 краски из имеющихся 7 различных?

Решение:

.

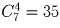
Задача 4:

У одного школьника есть 6 книг по математике, а у другого – 8. Сколькими способами они могут обменять три книги одного на три книги другого?

Решение:

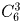
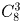
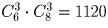
Первый школьник может выбрать 3 книги для обмена способами, второй – способами. Таким образом, число возможных обменов равно .

Задача 5:

В шахматном кружке занимаются 2 девочки и 7 мальчиков. Для участия в соревновании необходимо составить команду из четырех человек, в которую обязательно должна входить хотя бы одна девочка. Сколькими способами это можно сделать?

Решение:

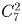
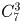
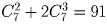
В команду входит либо одна девочка, либо две. Разберем оба случая. Если в команде две девочки, то двух мальчиков к ним можно добавить способами. Если же в команду входит только одна девочка (ее можно выбрать двумя способами), то команду можно дополнить тремя мальчиками различными способами. Таким образом, общее число возможных команд равно .

Задача 6:

Сколькими способами можно разбить 10 человек на две баскетбольные команды по 5 человек в каждой?

Решение:

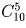
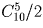
Первую команду можно выбрать способами. Этот выбор полностью определяет вторую команду. Однако при таком подсчете каждая пара команд А и В учитывается дважды: один раз, когда в качестве первой команды выбирается команда А, и второй, – когда в качестве первой команды выбирается команда В. Таким образом, ответ: .

Задача 7:

На плоскости отмечено 10 точек так, что никакие три из них не лежат на одной прямой. Сколько существует треугольников с вершинами в этих точках?

Решение:

.

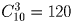
Задача 8:

Рота состоит из трех офицеров, шести сержантов и 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, двух сержантов и 20 рядовых?

Решение:

(n 8 + 1)(n 8 – 1) = n 16 – 1 = 0 (mod 17).

Задача 9:

На прямой отмечено 10 точек, а на параллельной ей прямой – 11 точек. Сколько существует а) треугольников; б) четырехугольников с вершинами в этих точках?

Решение:

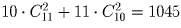
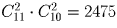
а) б) .

Задача 10:

Сколькими способами можно выбрать из 15 различных слов набор, состоящий не более чем из 5 слов?

Решение:

.

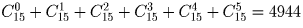
Задача 11:

Сколькими способами можно составить комиссию из 3 человек, выбирая ее членов из 4 супружеских пар, но так, чтобы члены одной семьи не входили в комиссию одновременно?

Решение:

Выберите сначала семьи, а потом в каждой паре конкретного представителя. Ответ: .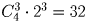

Задача 12:

В классе, в котором учатся Петя и Ваня – 31 человек. Сколькими способами можно выбрать из класса футбольную команду (11 человек) так, чтобы Петя и Ваня не входили в команду одновременно?

Решение:

Разберите три случая: в команду входит только Петя; в команду входит только Ваня; оба они в команду не входят. Ответ: .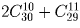

Задача 13:

Сколькими способами можно переставить буквы слова «ЭПИГРАФ» так, чтобы и гласные, и согласные шли в алфавитном порядке?

Решение:

Все определяется местами, на которых стоят гласные буквы. Ответ: .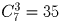

Задача 14:

Из 12 девушек и 10 юношей выбирают команду, состоящую из пяти человек. Сколькими способами можно выбрать эту команду так, чтобы в нее вошло не более трех юношей?

Решение:

.

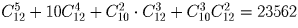
Задача 15:

Сколькими способами можно расставить 12 белых и 12 черных шашек на черных полях шахматной доски?

Решение:

.

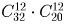
Задача 16:

а) Сколькими способами можно разбить 15 человек на три команды по 5 человек в каждой?

б) Сколькими способами можно выбрать из 15 человек две команды по 5 человек в каждой?

Решение:

а) ; б) .

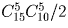
Задача 17:

Сколькими способами можно выбрать из полной колоды (52 карты) 10 карт так, чтобы

а) среди них был ровно один туз?

б) среди них был хотя бы один туз?

Решение:

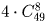
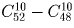
а) ; б) Перейдите к дополнению. Ответ: .

Задача 18:

Сколько существует 6-значных чисел, у которых по три четных и нечетных цифры?

Решение:

Разберите случаи в соответствии с тем, цифра какой четности стоит на первом месте. Затем в каждом случае выберите места для нечетных цифр. Ответ: .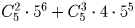

Задача 19:

Сколько существует 10-значных чисел, сумма цифр которых равна а) 2; б) 3; в) 4?

Решение:

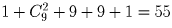
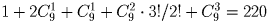
Разберите все возможные представления чисел 2, 3, 4 в виде суммы нескольких натуральных слагаемых. Не забывайте, что первая цифра – не ноль. Ответ: а) 10; б) ; в) .

Задача 20:

Человек имеет 6 друзей и в течение 5 дней приглашает к себе в гости каких-то троих из них так, чтобы компания ни разу не повторялась. Сколькими способами он может это сделать?

Решение:

.

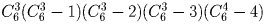
Задача 21:

Как известно, для участия в лотерее «Спортлото» нужно указать шесть номеров из имеющихся на карточке 45 номеров.

а) Сколькими способами можно заполнить карточку «Спортлото»?

б) После тиража организаторы лотереи решили подсчитать, каково число возможных вариантов заполнения карточки, при которых могло быть угадано ровно три номера. Помогите им в этом подсчете.

Решение:

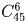
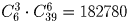
а) ; б) .

Источник

Сколькими способами можно переставить буквы слова девушка так чтобы гласные шли в алфавитном порядке

Сколькими способами можно положить в ряд 2 небесно-голубых лампочки и 4 лампочки цвета травы?

Сколькими способами можно положить в ряд 3 фисташковых лампочки и 5 лампочек цвета морской волны?

Сколькими способами можно переставить буквы слов: а) молоток; б) мисcисипи; в) математика?

б) Перестановку можно выполнить способами;

в) Перестановку можно выполнить способами.

Ответ: а) 840; б) 2 520; в) 151 200.

Сколькими способами можно переставить буквы слов: а) ротор; б) ревербератор; в) синхрофазатрон?

б) Перестановку можно выполнить способами;

в) Перестановку можно выполнить способами.

Ответ: а) 30; б) 3 326 400; в) 5 448 643 200.

Сколькими способами можно переставить буквы слов: а) самовар; б) кофеварка так, чтобы гласные и согласные буквы чередовались?

б) Это можно сделать способами.

Сколькими способами можно переставить буквы слов: а) поворот; б) переворот так, чтобы гласные и согласные буквы чередовались?

б) Это можно сделать способами.

Сколькими способами можно переставить буквы слова математика так, чтобы гласные и согласные буквы чередовались?

Сколькими способами можно переставить буквы слова стереометрия так, чтобы гласные и согласные буквы чередовались?

Сколькими способами можно переставлять буквы в слове перешеек так, чтобы четыре буквы е не шли подряд?

Сколькими способами можно переставлять буквы в слове алабама так, чтобы четыре буквы а не шли подряд?

У папы есть 2 дуриана, 3 фейхоа и 4 рамбутана. В течение 9 дней папа ежедневно даёт сыну по одному фрукту. Сколькими способами можно это делать?

Сколькими способами можно расставить восемь белых фигур (2 ладьи, 2 коня, 2 слона, ферзь и король) на первой линии шахматной доски?

Источник

21. Задачи

А) ,

Б) ,

В) ,

Г) ,

Д) ,

Е) .

Ответ: а); б) 4; в) 1; г) 42; д) 4; е) .

А) ,

Б) ,

В) ,

Г) ,

Д) ,

Е) .

Ответ: а) ; б) ; в) ; г) ; д) ; е) .

3. Решить уравнения (nÎ¥):

А) ,

Б) ,

В) ,

Г) ,

Д) ,

Е) .

Ответ: а) 8; б) 4; в) 10; г) 8; д) 5; е) 4.

4. Найти все n΢, удовлетворяющие условию:

А) ,

Б) ,

В) ,

Г) ,

Д) ,

Е) .

Ответ: а) ; б) ; в) ; г) ; д) ; е) .

5. Доказать справедливость равенств:

А) ,

Б) ,

В) ,

Г) ,

Д) ,

Е) .

6. Разложить по формуле бинома Ньютона и упростить:

А) ,

Б) ,

В) ,

Г) .

Ответ: а) ;

Б) ; в) ;

Г) .

7. Найти средние члены разложения:

А) ,

Б) .

Ответ: а) и ; б) .

8. Решите уравнения:

А) б) в)

9. У одного человека есть 7 книг по математике, а у другого – 9 книг. а) Сколькими способами они могут обменять книгу одного на книгу другого? б) То же самое, но меняются две книги одного на две книги другого.

Ответ: а) ; б) .

10. Несколько человек садятся за круглый стол. Будем считать, что два способа рассадки совпадают, если каждый человек имеет одних и тех же соседей в обоих случаях. а) Сколькими различными способами можно посадить четырех человек? б) семь человек? в) Во скольких случаях два данных человека из семи оказываются соседями? г) Во скольких случаях данный человек (из семи) имеет двух данных соседей?

Решение: а) Отношение соседства сохраняется при циклических перестановках и при симметричном отражении. В случае четырех человек мы имеем 2×4=8 преобразований, сохраняющих отношение соседства. Т. к. общее число перестановок 4 человек равно 4!=24, то имеем 24/8=3 различных способа рассадки.

Б) Если за столом сидят 7 человек, то имеем 7!/14=360 способов, вообще, а в случае n человек (n–1)!/2 способов.

В) Число способов, при которых 2 данных человека сидят рядом, вдвое больше числа способов посадить 6 человек (в силу возможности поменять этих людей местами). Значит оно равно .

Г) Находится аналогичным образом: .

11. Сколькими способами можно посадить за круглый стол 5 мужчин и 5 женщин так, чтобы никакие два лица одного пола не сидели рядом? Если они садятся не за круглый стол, а за карусель и способы, переходящие друг в друга при вращении карусели, считаются совпадающими.

Ответ:, .

12. Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт окажется хотя бы один туз? Во скольких случаях ровно один туз? Во скольких случаях не менее двух тузов? Ровно два туза?

Ответ:, , , .

13. В купе ж/д вагона имеется два противоположных дивана по 5 мест в каждом. Из 10 пассажиров четверо желают сидеть лицом к паровозу, а трое – спиной, остальным безразлично как сидеть. Сколькими способами могут разместиться пассажиры?

Решение: Сначала выберем, кто из трех пассажиров, кому безразлично как сидеть, сядет лицом к паровозу. Этот выбор можно сделать 3 способами. На каждом диване можно пересаживать пассажиров 5! Способами. Всего получаем способов.

14. У мамы 2 одинаковых яблока и 3 одинаковых груши. Каждый день в течение пяти дней подряд она выдает по одному фрукту. а) Сколькими способами это можно сделать? б) Если яблок m, а груш n. в) 2 яблок,3 груши, 4 апельсина.

Ответ: а) ; б) , в) .

15. У отца есть 5 различных апельсинов, которые он выдает своим 8 сыновьям так, что каждый получает либо один апельсин, либо ничего. Сколькими способами можно это сделать? Решите эту задачу при условии, что число апельсинов, получаемых каждым сыном, неограниченно.

Ответ: ; .

16. Из группы, состоящей из 7 мужчин и 4 женщин. Надо выбрать 6 человек так, чтобы среди них было не меньше 2 женщин. Сколькими способами можно это сделать?

Ответ: .

17. Найти сумму всех трёхзначных чисел, которые можно написать с помощью цифр 1, 2, 3, 4. А если никакая цифра не должна появляться дважды в записи каждого числа?

Решение: Всего таких чисел , в них цифр, каждая из 4 цифр употребляется раза – в каждом из трёх разрядов раз, поэтому сумма цифр первого разряда даст 16 (1+2+3+4)=160, второго –1600 и третьего –16000. Сумма равна 17760.

Если цифры не повторяются, то таких чисел , в них 72 цифры, каждая из 4 цифр употребляется в каждом из 3 разрядов 6 раз, поэтому сумма 6(1+2+3+4)(1+10+100)=6660.

18. Сколько различных четырехзначных чисел, делящихся на 4, можно составить из цифр 1,2, 3, 4, 5, если каждая цифра может встречаться в записи числа несколько раз? А если каждая цифра встречается лишь один раз?

Решение: Число должно оканчиваться: 12, 24, 32, 44, 52; первые же две цифры могут быть произвольными. Всего получаем чисел. Во втором случае число должно оканчиваться на одну из четырёх комбинаций: 12, 32, 52, 24; первые же две цифры могут быть выбраны из оставшихся трёх способами. Всего получаем 24 числа.

19. Компания из 7 юношей и 10 девушек танцует парами. а) Если в каком-либо танце участвуют все юноши, то сколько имеется вариантов участия девушек в этом танце? Сколько имеется вариантов, если учитывать лишь то, какие девушки остались неприглашенными? б) Решить те же вопросы, если относительно двух девушек можно с уверенностью утверждать, что они будут приглашены на танец.

Ответ: а) , . б) , .

20. Рота состоит из 3 офицеров, 6 сержантов, 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из одного офицера, двух сержантов и 20 рядовых? Решить эту задачу, при условии, что в отряд должны войти командир роты и старший из сержантов.

Ответ: ; .

21. На школьном вечере присутствуют 12 девушек и 15 юношей. Сколькими способами можно выбрать из них 4 пары для танца?

Ответ: .

22. Сколькими способами можно расставить 20 книг в книжном шкафу с 5 полками, если каждая полка может вместить все 20 книг?

Ответ: Добавим к 20 книгам 4 одинаковых разделительных предмета и рассмотрим все перестановки полученных объектов. Их число равно .

23. Сколькими способами можно надеть 5 различных колец на пальцы одной руки, исключая большой палец?

Ответ: Точно так же как предыдущей задаче .

24. 30 человек голосуют по 5 предложениям. Сколькими способами могут распределиться голоса, если каждый голосует за одно предложение и учитывается лишь число голосов, полученных за каждое предложение?

Решение: Так как учитывается лишь число голосов, поданных за каждое предложение, то надо распределить 30 одинаковых «предметов» по 5 «ящикам». Для этого добавим 4 одинаковых разделительных предмета и рассмотрим все перестановки полученных объектов. Их число равно . Каждой перестановке соответствует своё распределение голосов.

25. Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать, если в каждый цвет должны быть переплетены хотя бы одна книга?

Решение: 12 книг можно переплести в переплеты трёх цветов способами. Из них в случаях книги будут переплетены в не более чем два цвета, а в трех случаях – в один цвет. По формуле включений и исключений в случаях книги будут переплетены в переплеты всех цветов.

26. Сколькими способами можно выбрать 12 человек из 17, если данные двое человек из этих 17 не могут быть выбраны вместе?

Ответ: .

27. Хор состоит из 10 участников. Сколькими способами можно в течение трех дней выбирать по 6 участников, так, чтобы каждый день были различные составы хора?

Ответ: .

28. Человек имеет 6 друзей и в течение 20 дней приглашает к себе 3 из них так, что компания ни разу не повторяется. Сколькими способами можно это сделать?

Ответ: Так как , то каждый способ выбора компании будет использован ровно один раз. Число перестановок этих способов равно 20!

29. Для премии по математической олимпиаде выбраны 3 экземпляра одной книги, 2 экземпляра другой и 1 экземпляр третьей книги. Сколькими способами могут быть вручены премии, если в олимпиаде участвовало 20 человек и никому не дают две книги сразу? Если никому не дают двух экземпляров одной и той же книги, но могут быть вручены две или три различные книги?

Решение: Сначала выберем призеров, а потом распределим между ними книги. В результате по принципу умножения получаем способов. Во втором случае сначала выберем, кто получил первую книгу, потом, кто получил вторую, и, наконец, кому достанется третья книга. Всего получаем способов распределения премий.

30. Сколькими способами можно выбрать из 16 лошадей шестерку для запряжки так, чтобы вошли 3 лошади из шестерки ABCA’B’C’, но ни одна из пар AA’, BB’, CC’?

Решение: Выберем по одной лошади из каждой пары AA’, BB’, CC’ (8 способов выбора), трех лошадей из остальных 10 ( способов) и выберем порядок запрягания лошадей (6! способов). Всего способов.

31. Сколькими способами можно переставить буквы в слове «фатеция» так, чтобы не менялся порядок гласных букв?

Решение: Выпишем сначала гласные в данном порядке. Тогда для буквы «ф» имеем 5 мест. После того как они выписаны, имеем 6 мест для буквы «ц» и, наконец, 7 мест для буквы «м». Всего способов.

32. Сколькими способами можно переставить буквы в слове «параллелизм» так, чтобы не менялся порядок гласных букв?

Ответ: (следует учесть, что буква «л» входит в слово трижды.

33. Сколькими способами можно переставить буквы слова «Юпитер» так, чтобы гласные шли в алфавитном порядке?

Ответ: .

34. Сколькими способами можно переставить буквы слова «пастух» так, чтобы между двумя гласными были две согласные?

Ответ: Сначала фиксируем порядок гласных (2 способа), затем поставим между этими гласными 2 согласные ( способов). Первую из оставшихся согласных букв можно поставить до или после обеих гласных (два способа), а для второй имеем уже три места. Всего получаем способа.

35. Сколькими способами можно распределить 3n предметов между тремя людьми так, чтобы каждый получил n предметов?

Ответ: Расставим предметы в некотором порядке и отдадим первому человеку первые n предметов, второму – вторые n предметов и последнему – оставшиеся предметы. Поскольку порядок элементов в группах не играет роли, получаем .

36. Сколькими способами можно разложить 10 книг на 5 бандеролей по 2 книги в каждой (порядок бандеролей не принимается во внимание)?

Ответ: .

37. Сколькими способами можно раздать 18 различных предметов 5 участникам так, чтобы четверо из них получили по 4 предмета, а пятый – два предмета. Если трое получают по 4 предмета, а двое – по 3 предмета?

Решение: Располагаем участников раздела в некотором порядке. После этого располагаем всеми способами 18 предметов по порядку и делим на 4 группы по 4 предмета и 1 группу в 2 предмета. Группу в 2 предмета отдаём одному из 5 участников раздела, а остальные группы даём остальным (первую группу – первому, вторую – второму и т. д.) Так как порядок элементов в группах не играет роли, получаем способов раздела. Во втором случае точно так же получаем способов.

38. Сколькими способами можно раздать 27 книг лицам A, B и C так, чтобы A и B вместе получили вдвое больше книг, чем C?

Решение: Сначала выберем 9 книг для C. Это можно сделать способами. Оставшиеся 18 книг можно разделить между A и B 218 способами. Всего имеем способов раздела.

39. Сколькими способами можно выбрать из чисел от 1 до 100 три числа так, чтобы их сумма делилась на 3?

Решение: Возможны следующие случаи: на 3 делятся все три слагаемых, одно слагаемое и ни одного из слагаемых. В первом случае слагаемые можно выбрать способами. Во втором случае одно слагаемое дает в остатке 1, а другое – 2. Так как чисел от 1 до 100, дающих в остатке 1, имеется 34, а чисел, делящихся на 3, а также дающих в остатке 2, имеется по 33, то во втором случае имеем способов. Если все три слагаемых не делятся на 3, то они дают либо остатки 1, 1 и 1, либо 2, 2 и 2. Соответственно получаем или способов. Всего имеем способа.

40. Сколькими способами можно выбрать из 3n последовательных целых чисел три числа так, чтобы их сумма делилась на 3?

Ответ: .

41. На плоскости проведены 4 прямые линии, из которых никакие две не являются параллельными и никакие 3 не проходят через одну точку. Сколько получится треугольников?

42. На плоскости задано n точек, из которых p лежат на одной прямой, а кроме них никакие 3 точки не лежат на одной прямой. Сколько существует треугольников, вершинами которых являются эти точки?

Решение: Если бы никакие три из n точек лежат на одной прямой, то было бы треугольников с вершинами в этих точках. Но p точек лежат на одной прямой, и поэтому треугольников надо отбросить. Остается треугольников.

43. На прямой взяты p точек, а на другой прямой – ещё q точек. Сколько существует треугольников, вершинами которых являются эти точки?

Ответ: Можно взять две вершины на одной прямой, а третью – на другой. Поэтому получаем треугольников.

44. Каждая сторона квадрата разбита на n частей. Сколько можно построить треугольников, вершинами которых являются точки деления?

Решение: Треугольники могут быть двух видов: либо все три вершины лежат на разных сторонах квадрата, либо две вершины лежат на одной стороне квадрата, а третья – на какой-либо другой. В первом случае надо выбрать три стороны квадрата из четырех (), а потом на каждой из трех сторон по одной точке из n–1. Всего имеем способов выбора. Во втором случае надо выбрать сторону, где лежат две вершины (4 способа выбора) и две точки из n–1 ( способов), после чего выбрать одну из трёх оставшихся сторон (три способа) и точку на ней ( способов). Всего во втором случае имеем способов выбора. Итого получим способов.

45. Переплётчик должен переплести 12 различных книг в красный, зеленый и коричневый переплеты. Сколькими способами он может это сделать, если в каждый цвет должна быть переплетена хотя бы одна книга?

Решение: 12 книг можно переплести в переплеты 3 цветов 312 способами. Из них в случаях книги будут переплетены в не более чем два цвета, а в 3 случаях – в один цвет. По формуле включений и исключений получаем, что случаях книги будут переплетены всех трех цветов.

46. На столе лежат 20 билетов. Какова вероятность того, что 3 наудачу взятых билета имеют номер не больше 5?

Ответ: .

47. В одной урне 3 белых и 5 черных шаров, в другой – 9 белых и 4 черных. Из каждой урны взяли по три шара. Какова вероятность того, что шары будут одного цвета?

Ответ: .

48. Восемь различных книг случайных образом расставляют на полке. Найти вероятность того, что три определенные книги окажутся рядом?

Ответ: .

49. Зенитная батарея, состоящая из 3 орудий, производит залп по группе, состоящей из 7 самолетам. Каждое из орудий выбирает себе цель наудачу независимо от остальных. Найти вероятность того, что все орудия выстрелят по одному и тому же самолетам.

Ответ: .

50. Для уменьшения общего количества игр 12 команд случайным образом разбиты на две равные подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся в разных подгруппах.

Ответ: .

51. Для уменьшения общего количества игр 2n команд случайным образом разбиты на две равные подгруппы. Определить вероятность того, что две наиболее сильные команды окажутся: а) в разных подгруппах; б) в одной подгруппе.

Ответ: а) , б) .

52. Зенитная батарея, состоящая из k орудий, производит залп по группе, состоящей из l самолетов (k£l). Каждое орудие выбирает себе цель случайно и независимо от других. Найти вероятность того, все k орудий выстрелят по одной и той же цели.

Ответ: .

Ответ: а) , б) .

Ответ: а) , б) .

55. На бочонках лото написаны числа от 1 до N. Из этих N бочонков одновременно случайно выбираются два. Найти вероятность того, что: а) на обоих бочонках написаны числа, меньше чем k (2 2). Найти вероятность того, что два фиксированных лица А и В окажутся рядом.

Ответ: .

57. N человек случайным образом рассаживаются за прямоугольным столом вдоль одной из его сторон (N>2). Найти вероятность того, что два определенных лица А и В окажутся рядом.

Ответ: .

Ответ: .

Источник