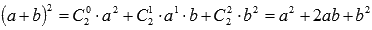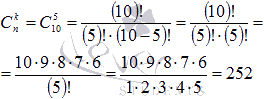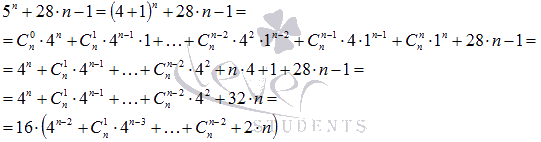понятие о свойствах биномиальных коэффициентов можно отнести к метапредметным

Расчет биномиальных коэффициентов на Си (С++) и Python

При решении задач комбинаторики часто возникает необходимость в расчете биномиальные коэффициентов. Бином Ньютона, т.е. разложение также использует биномиальные коэффициенты. Для их расчета можно использовать формулу, выражающую биномиальный коэффициент через факториалы: или использовать рекуррентную формулу: Из бинома Ньютона и рекуррентной формулы ясно, что биномиальные коэффициенты — целые числа. На данном примере хотелось показать, что даже при решении несложной задачи можно наступить на грабли.
Прежде чем перейти к написанию процедур расчета, рассмотрим так называемый треугольник Паскаля.

или он же, но немного в другом виде. В левой колонке строки значение n, дальше в строке значения для k=0..n

В полном соответствии с рекуррентной формулой значения равны 1 и любое число равно сумме числа, стоящего над ним и числа «над ним+шаг влево». Например, в 7й строке число 21, а в 6й строке числа 15 и 6: 21=15+6. Видно также, что значения в строке симметричны относительно середины строки, т.е. . Это свойство симметричности бинома Ньютона относительно a и b и оно видно в факториальной формуле.
Ниже для биномиальных коэффициентов я буду также использовать представление C(n,k) (его проще набирать, да и формулу-картинку не везде можно вставить.

Расчет биномиальных коэффициентов через факториальную формулу

поскольку биномиальные коэффициенты неотрицательные, будем использовать в расчетах беззнаковый тип.

Значение в очередной строке должно быть примерно в 2 раза больше, чем в предыдущей. Поэтому последний правильно вычисленный коэффициент (см треугольник выше) — это C(12,6) Хотя unsigned int вмещает 4млрд, правильно вычисляются значения меньше 1000. Вот те раз, почему так? Все дело в нашей процедуре bci, точнее в строке, которая сначала вычисляет большое число в числителе, а потом делит его на большое число в знаменателе. Для вычисления C(13,6) сначала вычисляется 13!, а это число > 6млрд и оно не влезает в unsigned int.
Как оптимизировать расчет ? Очень просто: раскроем 13! и сократим числитель и знаменатель на 7! В результате получится . Запрограммируем расчет по этой формуле

Явно лучше, ошибка возникла при расчете C(31,15). Причина понятна — все то же переполнение. Сначала умножаем на 31 (оп-па — переполнение, потом делим на 15). А что, если использовать рекурсивную формулу? Там только сложение, переполнения быть не должно.
Что ж, пробуем:

Все, что влезло в unsigned int, посчиталось правильно. Вот только строчка с n=34 считалась около минуты. При расчете C(n,n/2) делается два рекурсивных вызова, поэтому время расчета экспоненциально зависит от n. Что же делать — получается либо неточно, либо медленно. Выход — в использовании 64 битных переменных.

Замечание по результатам обсуждений: в конце статьи добавлен раздел, где приведен простой и быстрый вариант «bcr с запоминанием» одного из участников обсуждения.

Использование 64 битных типов для расчета C(n,k)

2.8*10 19 уже не влезает в unsigned long long

Дальнейшее повышение точности и расчет при n>67

Для экстремалов и «олимпийцев»

В принципе, для практических задач точности функции bcd достаточно, но в олимпиадных задачах часто даются тесты «на грани». Т.е. теоретически может встретится задача, где точности double недостаточно и C(n,k) влезает в unsigned long long еле-еле. Как избежать переполнения для таких крайних случаев? Можно использовать рекурсивный алгоритм. Но если он для n=34 считал минуту, то для n=67 будет считать лет 100. Можно запоминать рассчтанные значения (см Дополнение после публиукации).Также можно использовать рекурсию не для всех n и k, а только для «достаточно больших». Вот процедура расчета, которая считает правильно для n 67 при малых k (к примеру, считает C(82,21)=1.83*10 19 ).

В какой-то из олимпиадных задач мне потребовалось вычислять много C(n,k) для n >70, т.е. они заведомо не влезали в unsigned long long. Естественно, пришлось использовать «длинную арифметику» (свою). Для этой задачи я написал «рекурсию с памятью»: вычисленные коэффициенты запоминались в массиве и экспоненциального роста времени расчета не было.

Дополнение после публикации

При обсуждении часто упоминаются варианты с запоминанием рассчитанных значений. У меня есть код с динамическим выделением памяти, но я его не привел. На даный момент вот самый простой и эффективный из комментария chersanya: http://habrahabr.ru/post/274689/#comment_8730359http://habrahabr.ru/post/274689/#comment_8730359

Если в программе надо использовать [почти] все коэффициенты треугольника Паскаля (до какого-то уровня), то приведенный рекурсивный алгоритм с запоминанием — самый быстрый способ. Аналогичный код годится и для unsigned long long и даже для длинной арифметики (хотя там, наверное, лучше динамически вычислять и выделять требуемый объем памяти). Конкретные значения N_MAX могут быть такими:
35 — посчитает все коэффициенты C(n,k), n 19
K_MAX — это может быть N_MAX/2+1, но не больше 35, поскольку C(68,34) за границей unsigned long long.
Для простоты можно всегда брать K_MAX=35 и не думать «войдет — не войдет» (до тех пор, пока не перейдем к числами с разрядностью >64 бита).

Расчет биномиальных коэффициентов на Python

Это дополнение появилось спустя примерно погода после публикации статьи. Автор начал осваивать Python и для тренироки я решаю олимпиадные задачи, сделанные ранее на C++. Для задач связанных в точными/длинными вычислениями приходится либо всячески исхитряться (как при расчетах биномиальных коэфиициентов), дабы избежать раннего переполнения, либо смиряться с потерей точности (перейдя к типу double) либо писать(или искать) длинную арифметику. В Python длинная арифметика уже есть, поэтому тут для вычисления биномиальных коэффициентов достаточно реализовать запоминание. Запоминать их будем в списке (передается в функцию как папаметр).

Вот вывод (без таблички)
270288240945436569515614693625975275496152008446548287007392875106625428705522193898612483924502370165362606085021546104802209750050679917549894219699518475423665484263751733356162464079737887344364574161119497604571044985756287880514600994219426752366915856603136862602484428109296905863799821216320
0.4200884663301988
Меньше полсекуды для такого коэффициента
C(68,34) (напомню — он не влезает в long long) считается за 0.017 сек и равен 28453041475240576740

Источник

Метапредметный подход в преподавании математики.

Ищем педагогов в команду «Инфоурок»

МБОУ «СШ №12»,г Нижневартовск

Латыпова Зугура Минигалимовна,

учитель математики высшей категории

Метапредметный подход в преподавании математики.

В статье рассматривается проблема формирования субъектной позиции школьника при освоении предметных и метапредметных умений на уроках математики. Предлагается модель формирования умственных действий, построенная на принципах детельностного подхода в обучении. Определены общие подходы к организации образовательного процесса на уроках математики.

Ключевые слова: метапредмет, метапредметный урок, субъект учебной деятельности; рефлексия; умственное действие; метапредметные методы; метапредметные результаты метапредметная среда.

« Не мыслям следует учить, а мыслить» И.Кант

В Федеральном государственном образовательном стандарте среднего (полного) общего образования появился новый термин – метапредметный. Установленные стандартом новые требования к результатам обучающихся вызывают необходимость в изменении содержания обучения на основе принципов метапредметности как условия достижения высокого качества образования. Учитель сегодня должен стать конструктом новых педагогических ситуаций, новых заданий, направленных на использование обобщенных способов деятельности и создание учащимися собственных продуктов в освоении знаний. Что такое метапредметность, метапредметы? Где их взять (или как их разработать?).

Вот почему перед школой остро встала и в настоящее время остаётся актуальной проблема самостоятельного успешного усвоения учащимися новых знаний, умений и компетенций, включая умение учиться. Большие возможности для этого предоставляет освоение универсальных учебных действий (УУД). Именно поэтому «Планируемые результаты» Стандартов образования (ФГОС) второго поколения определяют не только предметные, но метапредметные и личностные результаты.

Для введения новых стандартов учитель должен идти на шаг впереди и уже быть готов к новому. Учитель сегодня – конструктор новых педагогических ситуаций, новых заданий, направленных на использование обобщённых способов деятельности и создание учащимися новых продуктов в освоении знаний.

Сегодня понятия «метапредмет», «метапредметное обучение» приобретают особую популярность. Это вполне объяснимо, ведь метапредметный подход заложен в основу новых стандартов. В новой версии ФГОС впервые сказано о необходимости и о требованиях к метапредметному образовательному результату обучения.

Введение метапредметного подхода в образовании — попытка осторожно, постепенно, без всяких резких революционных реформ развернуть образование навстречу новым потребностям века.

Метапредмет выстраивается вокруг какой-то мыследеятельностной организованности. В качестве таких мыследеятельностных организованностей могут быть знание, знак, проблема, задача, смысл, категория. Все они имеют деятельностный, а потому универсальный метапредметный характер. На их основе могут быть выстроены учебные предметы нового типа.

Метапредметность характеризует выход за предметы, но не уход от них. Метапредмет – это то, что стоит за предметом или за несколькими предметами, находится в их основе и одновременно в корневой связи с ними. Метапредметность не может быть оторвана от предметности

1. Взгляды ученых на метапредмет.

Метапредметные результаты (по А.Г. Асмолову) включают освоенные обучающимися универсальные учебные действия (познавательные, регулятивные и коммуникативные), обеспечивающие овладение ключевыми компетенциями, составляющими основу умения учиться[6].

Метапредметы (по А.В. Хуторскому): «Метапредметное содержание, то есть то, что предшествует учебному предмету, как бы находится за ним, существует до его конкретного проявления». «Наличие фундаментального образовательного объекта». Примеры метапредметов: «Числа», «Буквы», «Культура», «Мироведение»[7], [8].

В любой деятельности есть: а) то, что делает ее содержательной, то есть ПРЕДМЕТНАЯ составляющая; б) то, что делает ее осознанной и ответственной, то есть МЕТАПРЕДМЕТНАЯ составляющая.

МЕТАПРЕДМЕТНАЯ составляющая деятельности «ОБУЧАЮСЬ»:

Стратегическая (мотив, цель, план, средства, организация, действия, результат, анализ и др.);

исследовательская (факт, проблема, гипотеза, проверка-сбор новых фактов, вывод и др.)

проектировочная ( замысел, реализация, рефлексия и др.);

конструирующей (выстраивание системы мыслительных операций, выполнение эскизов, рисунков, чертежей, позволяющих конкретизировать и детализировать проект и др.);

прогнозирующей (мысленное конструирование будущего состояния объекта на основе предвидения и выстраивание вариантов сценария разворачивания событий и др.

2. Принцип метапредметности можно реализовать в разных форматах:

МЕТАПРЕДМЕТНЫЙ КОМПОНЕНТ в содержании предметного учебного курса – открытие для учащихся смысла форм, видов и приемов разнообразной учебной деятельности, целенаправленное обучение таким способам деятельности.

Осознанный выбор содержания, видов и форм ВНЕУРОЧНОЙ ДЕЯТЕЛЬНОСТИ в соответствии с требованиями ФГОС к образовательным МЕТАПРЕДМЕТНЫМ результатам.

3. Особенности метапредметного урока математики

Для того чтобы оптимизировать учебный процесс, повысить его эффективность, современный ученик и педагог при свободном доступе к информации должны обладать умениями приобретать, сохранять, творчески ее интерпретировать в обучении и профессиональной деятельности использую интерактивные методы обучения.

Метапредметный урок математики предполагает синтез предметных знаний. Целью, урока является в первую очередь преодоление разобщенности различных учебных дисциплин, отказ от узкопредметной специализации. Таким образом, метапредметный урок является синтезом учебных предметов, формирующим целостное восприятие окружающего мира.

На уроках математики с использованием элементов метапредметных технологий происходит выведение учителя и ученика к надпредметному основанию, которым является сама деятельность ученика и педагога. В ходе движения в метапредмете ребенок осваивает сразу два типа содержания – содержание предметной области и деятельность Включение ребенка в разные типы деятельности связано с анализом своеобразных способов действия каждого конкретного ребенка, что создает условия для его личностного роста

1. Это интегрированный урок, с применением ИКТ.

2. Деятельность учащихся организуется не с целью передачи им знаний, а с целью передачи способов работы со знанием.

3. Содержание составляют деятельностные единицы, носящие универсальный характер: понятия, модели, схемы, задачи, проблемы и т.д.

4. Учитель должен хорошо знать свой предмет и его возможности.

5. Системная работа со способом: если ученик освоил решение задач на три параметра в математике, учитель даёт ему решение задачи этого же типа, но из « реальной математики».

6. Ядром творческого метапредметного урока является образовательная ситуация: необходимо заранее продумать и сформулировать одну или несколько ключевых проблем, с помощью которых ученики захотят и смогут проявить себя. Проблема или тема должна быть “острая», носить метапредметный характер.

7. Педагог заранее отбирает культурно-исторические аналоги, которые будут предложены ученикам по рассматриваемой проблеме.

8. Педагог заранее определяет:

каким образом он предполагает обеспечить рефлексию учеником своей деятельности (конкретный способ, или прием, или задание);

как оценить внешний и внутренний образовательный продукт ученика?

с помощью, каких критериев оценит успешность проведения метапредметного занятия.

9. Работа учащихся оформляется виде наглядного продукта (учебную среду ученики создают сами), поэтому заранее необходимо продумать конкретный предвосхищаемый образовательный продукт, который должны будут создать ученики за время занятия. Продукт должен быть конкретный, но без известного для педагога содержания.

Метапредметные результаты определяются как освоенные обучающимися межпредметные понятия и универсальные учебные действия, способность их ис­пользования в учебной, познавательной и социальной практике, самостоятель­ность планирования и осуществления учебной деятельности и организации учеб­ного сотрудничества с педагогами и сверстниками, построение индивидуальной образовательной траектории [1].

4. Процесс освоения способов выполнения действий и этапы метапредметного урока математики.

Этап 1. Для введения учащихся в ситуацию, требующую выполнения действия необходимо предложить конкретно – практическую задачу, в структуру которой входит формируемое действие. Обучаемый в сотрудничестве с учителем должен перевести эту задачу в учебную. Любой вопрос или тема излагаются вначале самими учениками на их уровне представлений, образов и мышления. Достигается это путем создания особых образовательных ситуаций, проблемных вопросов. Ответы и мнения детей обсуждаются, сопоставляются, комментируются. Оценки учителя типа «правильно- неправильно» отсутствуют.

Этап 2. Определение критериев и способов оценки результата действия предполагает поиск ответа на вопрос: «Каким требованиям должен удовлетворять результат действия и как мы будем проверять, соответствует ли он этим требованиям?».

Этап 3. Планирование действия позволяет составить последовательность операций, выполнение которых позволит получить результат.

Этап 4. Выполнение действия и оценка результатов предполагает ряд важных моментов: контроль выполнения действия в соответствии с разработанным планом, оценка результата в соответствии с разработанными критериями и способами оценки. Учащиеся создают собственный образовательный продукт – рисунок, версию, таблицу, схему. Учитель приводит и обсуждает с учениками цитаты из первоисточников, сравнивает определения, которые дали ученики, с теми, которые имеются у учёных, размещены в словарях и энциклопедиях, в параграфе учебника и др. источниках. В результате дети развивают свои предварительно выращенные понимания, либо переопределяют их, выбирая близкую им позицию другого ученика или ученого. В любом случае происходит сопоставление изучаемого материала с лично создаваемым учеником содержанием.

Этап 5. Обсуждение результата и способа выполнения действия (рефлексия способа). На этом этапе необходимо установить насколько результат действия соответствует или не соответствует предъявляемым к нему требованиям. В случае несоответствия учащиеся осуществляют поиск причин этих недостатков. В итоге каждый ученик говорит о том, что у него лучше всего получилось, как он пришел к своему результату, что ему больше всего понравилось, запомнилось. Данный этап называется рефлексивным. Его задача – осознать каждым учеником его результаты, трудности, способы собственной деятельности. На базе рефлексивного этапа происходит самооценка и оценка образовательных результатов Если результат достигнут, то учащиеся обосновывают причины успеха.

Этап 6. Если будут выявлены недостатки способа действий осуществляется «коррекции» способа действия. Необходимо ответить на вопрос: «Что нужно сделать, чтобы улучшить способ действия и получить нужный результат?»

Этап 7. Действие выполняется повторно.

Этап 8. Оценка и обсуждение результата и способа повторного выполнения действия [ 11].

5. Эффективные инструменты достижения метапредметных результатов в образовательном процессе

Образование – это институт социализации, а благодаря Интернету современная школа утрачивает монополию в сфере воспитания и социализации подрастающего поколения. Интернет – это ключевая социальная инновация современной информационной эпохи. Новые стандарты диктуют новое содержание образования. Сегодня активное использование ИКТ в образовании способствует формированию креативной, развитой личности. Для достижения личностного, профессионального успеха уже созданы условия повышения качества, мобильности, доступности ЭОР.

Учитель организует деятельность ученика в инновационной образовательной среде, используя преимущество современных технологий сетевого взаимодействия, заключающиеся во взаимосвязи двух продпространств – непосредственно личного взаимодействия участников проекта (офф-лайн) и взаимодействия через Интернет-ресурсы и коммуникативные площадки Интернета (он-лайн).

Фундаментальный образовательный объект – общий для учащихся объект познания, который обеспечивает каждому из них личный результат его познавательной деятельности.

Примеры фундаментальных объектов:

Источник

Расчет биномиальных коэффициентов с использованием Фурье-преобразований

При решении задач комбинаторики часто возникает необходимость в расчете биномиальных коэффициентов. Бином Ньютона, т.е. разложение также использует биномиальные коэффициенты. Для их расчета можно использовать формулу, выражающую биномиальный коэффициент через факториалы: или использовать рекуррентную формулу: Из бинома Ньютона и рекуррентной формулы ясно, что биномиальные коэффициенты — целые числа.

Одним из методов, позволяющих значительно сократить количество вычислений, является применение Фурье преобразований и дискретных Фурье преобразований.

Наличие большого числа библиотек, реализующих Фурье преобразований (во всевозможных вариантах быстрых версий), делает реализацию алгоритмов не очень сложной задачей для программирования.
Реализованные алгоритмы являются частью библиотеки с открытым исходным кодом FFTTools. Интернет-адрес: github.com/dprotopopov/FFTTools

Преобразование Фурье функции f вещественной переменной является интегральным и задаётся следующей формулой:

Разные источники могут давать определения, отличающиеся от приведённого выше выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Но все свойства будут те же, хотя вид некоторых формул может измениться.

Кроме того, существуют разнообразные обобщения данного понятия.

Дискретное преобразование Фурье

Дискретное преобразование Фурье (в англоязычной литературе DFT, Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов. Существуют многомерные дискретные преобразования Фурье.

Формулы дискретных преобразований

Дискретное преобразование Фурье является линейным преобразованием, которое переводит вектор временных отсчётов в вектор спектральных отсчётов той же длины. Таким образом преобразование может быть реализовано как умножение симметричной квадратной матрицы на вектор:

Свёртка двух функций

Фурье-преобразования для вычисления свёртки

Одним из замечательных свойств преобразований Фурье является возможность быстрого вычисления корреляции двух функций определённых, либо на действительном аргументе (при использовании классической формулы), либо на конечном кольце (при использовании дискретных преобразований).

И хотя подобные свойства присущи многим линейным преобразованиям, для практического применения, для вычисления операции свёртки, согласно данному нами определению, используется формула

Биномиальные коэффициенты

Рассмотрим полином F(x)=1+x и его свёртку с самим собой n раз
Fx..xF = SUM С( i, n-1 )*x^i = BFT ( FFT(F)*. *FFT(F) ) = BFT ( FFT(F)^(n-1) )
То есть биномиальные коэффициенты С( i, n-1 ) могут быть получены из значений коэффициентов полинома (1+x)^(n-1)

Программируем:

Проверяем:

Зачем?

При вычислении с помощью треугольника Паскаля трудоёмкость имеет оценку O(n^2).
При вычислении с помощью быстрых Фурье-преобразований трудоёмкость имеет оценку O(n*log n).

Источник

Свойства биномиальных коэффициентов.

Лекция № 9. Формула бинома Ньютона. Свойства биноминальных коэффициентов. Треугольник Паскаля.

Формула бинома Ньютона

Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид. где. — биномиальные коэффициенты, — неотрицательное целое число.

Для натуральных n имеет вид

, где — биномиальные коэффициенты, представляющие из себя сочетания из n по k, k=0,1,2,…,n, «!» – это знак факториала).

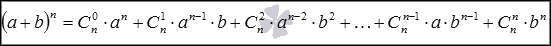
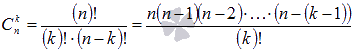
Формула сокращенного умножения «квадрат суммы» раскладывается согласно формуле бинома Ньютона:

т.е.представляет собой частный случай бинома Ньютона при n=2.

— выражение в правой части формулы бинома Ньютона, называют разложением выражения (a+b) n ;

Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля.

Треугольник Паскаля.

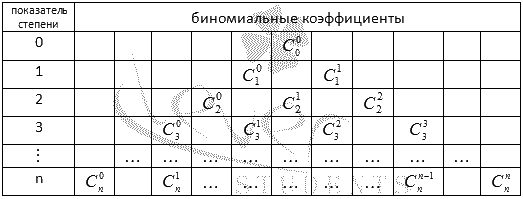
Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля.

В общем виде треугольник Паскаля имеет следующий вид:

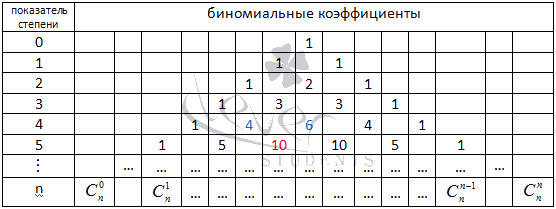
Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n:

Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.

Свойства биномиальных коэффициентов.

Для коэффициентов бинома Ньютона справедливы следующие свойства:

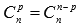
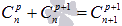
· коэффициенты, равноудаленные от начала и конца разложения, равны между собой , p=0,1,2,…,n;

· ;

· сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома Ньютона: ;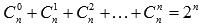

· сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.

Напишите разложение выражения (a+b) 5 по формуле бинома Ньютона.

Смотрим на строку треугольника Паскаля, соответствующую пятой степени (п.2.1). Биномиальными коэффициентами будут числа 1, 5, 10, 10, 5, 1.

Таким образом, имеем .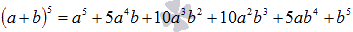

Найдите коэффициент бинома Ньютона для шестого члена разложения выражения .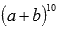

В нашем примере n=10, k=6-1=5. Таким образом, мы можем вычислить требуемый биномиальный коэффициент:

Доказать, что значение выражения 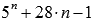, где n – натуральное число, делится на 16 без остатка.

Представим первое слагаемое выражение как 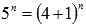и воспользуемся формулой бинома Ньютона:

Согласно формуле бинома Ньютона имеем:

Раскладываем по формуле бинома Ньютона:

С₅ 0 *(х 2 ) 5 + С₅ 1 *(х 2 ) 4 * (-2y) + С₅ 2 *(х 2 ) 3 * (-2y) 2 + С₅ 3 *(х 2 ) 2 * (-2y) 3 + С₅ 4 *(х) 2 * (-2y) 4 + С₅ 5 * (-2y) 5

По треугольнику Паскаля для n = 5 (см. п.2.1) определяем значения биноминальных коэффициентов:

Подставляем в формулу бинома Ньютона:

1*(х) 10 + 5*(х) 8 * (-2y) + 10*(х) 6 * (-2y) 2 + 10*(х) 4 * (-2y) 3 + 5*(х) 2 * (-2y) 4 + 1* (-2y) 5

Источник