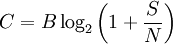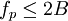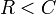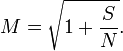по мнению к шеннона точности передачи информации можно добиться за счет увеличения ответ сигнала

Эффективность передачи данных и теория информации

Кодирование информации в простейшей форме зародилось при общении людей в виде жестовых кодов, а позднее в виде речи, суть которой кодовые слова для передачи наших мыслей собеседнику, далее наступил новый этап развития такого кодирования – письменность, которая позволяла хранить и передавать информацию с наименьшими потерями от писателя к читателю. Иероглифы – есть конечный алфавит, обозначающий понятия, предметы или действия, элементы которого в каком-то виде заранее оговорены людьми для однозначного «декодирования» записанной информации. Фонетическое письмо использует буквенный алфавит для внутреннего кодирования слов речи и так же служит для однозначного воспроизведения записанной информации. Цифры позволяют использовать кодовое представление вычислений. Но данные типы кодирования служили скорее для непосредственного общения, но людям требовалось так же передавать информацию на расстояние и достаточно быстро, как следствие появились простейшие системы телекоммуникаций.

Важнейшим скачком в истории развития передачи информации стало использование цифровых систем передачи данных. Использование аналоговых сигналов требует большой избыточности информации, передаваемой в системе, а так же обладает таким существенным недостатком как накапливание помех. Различные формы кодирования для преобразования аналоговых сигналов в цифровые, их хранения, передачи и преобразования обратно в аналоговую форму начали своё бурное развитие во второй половине XX века, и к началу XXI практически вытеснили аналоговые системы.

Основная проблема, которую необходимо решить при построении системы коммуникации, была впервые сформулирована Клодом Шенноном в 1948 году:

Главное свойство системы связи заключается в том, что она дольно точно или приближенно воспроизвести в определенной точке пространства и времени некоторое сообщение, выбранное в другой точке. Обычно, это сообщение имеет какой-то смысл, однако это совершенно не важно для решения поставленной инженерной задачи. Самое главное заключается в том, что посылаемое сообщение выбирается из некоторого семейства возможных сообщений.

Такая точная и ясная постановка проблемы коммуникации оказала огромное воздействие на развитие средств связи. Возникла новая научная отрасль, которая стала называться теорией информации. Главная идея, обоснованная Шенноном, заключается в том, что надежные коммуникации должны быть цифровыми, т.е. задачу связи следует рассматривать как передачу двоичных цифр (битов). Появилась возможность однозначно сравнить переданную и принятую информацию.

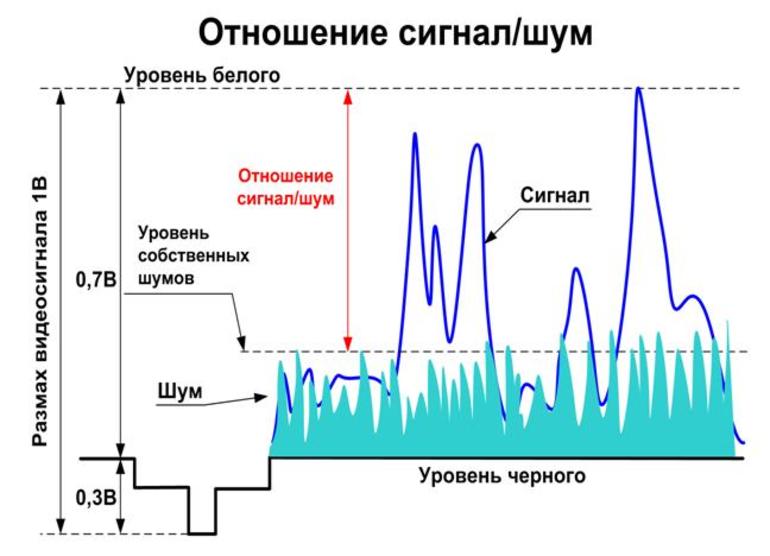
Заметим, что любой физический канал передачи сигналов не может быть абсолютно надежным. Например, шум, который портит канал и вносит ошибки в передаваемую цифровую информацию. Шеннон показал, что при выполнении некоторых достаточно общих условий имеется принципиальная возможность использовать ненадежный канал для передачи информации со сколь угодно большой степенью надежности. Поэтому нет необходимости пытаться очистить канал от шумов, например, повышая мощность сигналов (это дорого и зачастую невозможно). Вместо этого следует разрабатывать эффективные схемы кодирования и декодирования цифровых сигналов.

Задача кодирования канала (выбор сигнально-кодовой конструкции) заключается в построении на основе известных характеристик канала кодера, посылающего в канал входные символы, которые будут декодированы приемником с максимальной степенью надежности. Это достигается с помощью добавления в передаваемую цифровую информацию некоторых дополнительных проверочных символов. На практике каналом может служить телефонный кабель, спутниковая антенна, оптический диск, память компьютера или еще что-то. Задачей кодирования источника является создание кодера источника, который производит компактное (укороченное) описание исходного сигнала, который необходимо передать адресату. Источником сигналов может служить текстовый файл, цифровое изображение, оцифрованная музыка или телевизионная передача. Это сжатое описание сигналов источника может быть неточным, тогда следует говорить о расхождении между восстановленным после приема и декодирования сигналом и его оригиналом. Это обычно происходит при преобразовании (квантовании) аналогового сигнала в цифровую форму.

Если скорость передачи сообщений меньше пропускной способности канала связи, то существуют коды и методы декодирования такие, что средняя и максимальная вероятности ошибки декодирования стремятся к нулю, когда длина блока стремится к бесконечности
Иными словами: Для канала с помехами всегда можно найти такую систему кодирования, при которой сообщения будут переданы со сколь угодно большой степенью верности, если только производительность источника не превышает пропускной способности канала.

Если скорость передачи больше пропускной способности, то есть, то не существует таких способов передачи, при которых вероятность ошибки стремится к нулю при увеличении длины передаваемого блока.

Для аддитивного белого гауссова шума Шеннон получил следующее выражение:
, где
C — пропускная способность канала, бит/с;
W — ширина полосы канала, Гц;
S — мощность сигнала, Вт;
N — мощность шума, Вт.

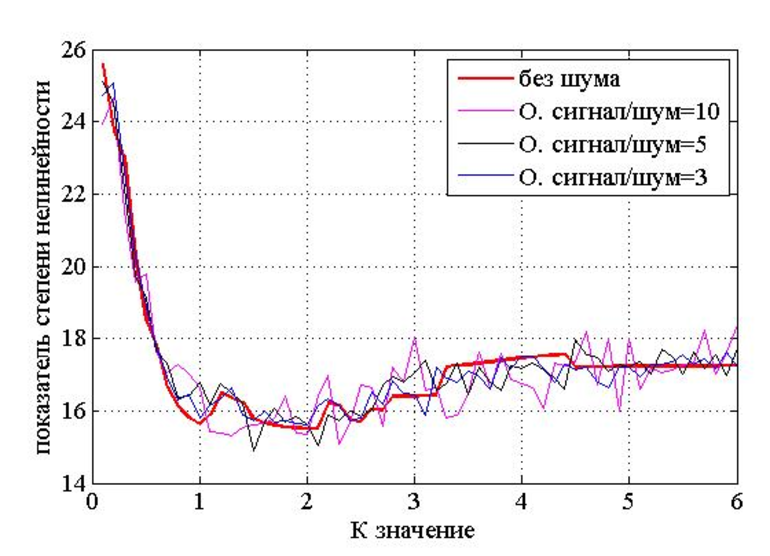
(График для наглядности, зависимость C(W,P) при N₀=const; значения с потолка, попрошу на них не смотреть)
Т.к. мощность АБГШ растёт линейно с шириной полосы канала, имеем, что пропускная способность канала имеет предел C_max=(S/N₀)log(2), при бесконечно широкой частотной полосе (который растёт линейно по мощности).

, где
η — эффективность использования спектра, бит/с/Гц;
T_R — скорость передачи информации, бит/с;
W — ширина полосы канала, Гц.

Тогда, , используя значение энергии бита (для сигналов со сложными сигнально кодовыми конструкциями я понимаю среднее значение энергии на бит) и , где
k — количество бит на символ, передаваемый в канал;
T — длительность символа, с;
R — скорость передачи в канале, бит/с;
E_b — энергия на передачу одного бита в канале;
N₀ — спектральная плотность мощности шума, Вт/Гц;
получим или .

Предел Шеннона будет иметь вид:

Данный предел имеет смысл для каналов без кодеков (R = T_R), для достижения такой эффективности принимаемое слово должно быть бесконечной длины. Для каналов с использованием кодеков помехоустойчивого кодирования под E_b следует понимать энергию на передачу одного информационного, а не канального бита (тут возможны разночтения и я готов выслушать альтернативные версии) => E_b/N₀ в канале отлично от этого значения в зависимости от скорости кода (1/2, 3/4, 7/8… )

Таким образом видим, что существует предел отношения сигнал/шум в канале (E_b/N₀) такой, что невозможно построить систему передачи данных, в которой можно добиться сколь угодно малой вероятности ошибки, при большем уровне шума (может существовать система с просто малой вероятностью ошибки, при предельном отношении!).

Литература

Галлагер Р. «Теория информации и надёжная связь» – М.: «Советское радио», 1974.
Сэломон Д. «Сжатие данных, изображений и звука» – М.: «Техносфера», 2004

Спасибо за внимание, в качестве продолжения, если интересно, могу написать статью с иллюстрациями и сравнением эффективности сигнально-кодовых конструкций по отношению к границе Шеннона.

Источник

Теорема Шеннона-Хартли

Теорема Шеннона-Хартли

Теорема Шеннона-Хартли в теории информации — применение теоремы кодирования канала с шумом к архетипичному случаю непрерывного временного аналогового канала коммуникаций, искаженного гауссовским шумом. Теорема устанавливает шенноновскую ёмкость канала, верхнюю границу максимального количества безошибочных цифровых данных (то есть, информации), которое может быть передано по такой связи коммуникации с указанным полоса пропускания в присутствии шумового вмешательства, согласно предположению, что мощность сигнала ограничена, и Гауссовский шум характеризуется известной мощностью или мощностью спектральной плотности. Закон назван в честь Клода Шеннона и Ральфа Хартли.

Содержание

Утверждение теоремы

Рассматривая все возможные многоуровневые и многофазные методы шифрования, теорема Шеннона-Хартли утверждает, что ёмкость канала C, означающая теоретическую верхнюю границу скорости передачи данных, которые можно передать с данной средней мощностью сигнала S через аналоговый канал связи, подверженный аддитивному белому гауссовскому шуму мощности N равна:

C — ёмкость канала в битах в секунду; B — полоса пропускания канала в герцах; S — полная мощность сигнала над полосой пропускания, измеренной в ваттах или вольтах в квадрате; N — полная шумовая мощность над полосой пропускания, измеренной в ваттах или вольтах в квадрате; S/N — отношение сигнала к шуму(SNR) сигнала к гауссовскому шуму, выраженное как отношение мощностей.

История развития

В течение конца 1920-ых Гарри Найквист и Ральф Хартли разработали фундаментальные идеи, связанные с передачей информации, с помощью телеграфа как система коммуникаций. В то время, это был прорыв, но науки как таковой не существовало. В 1940-ых, Клод Шеннон ввел понятие способности канала, которое базировалось на идеях Найквиста и Хартли, а затем сформулировал полную теорию передачи информации.

Критерий Найквиста

Формула Хартли

Теоремы Шеннона для канала с шумами

Теоремы Шеннона для канала с шумами (теоремы Шеннона для передачи по каналу с шумами) связывают пропускную способность канала передачи информации и существование кода, который возможно использовать для передачи информации по каналу с ошибкой, стремящейся к нулю (при увеличении длины блока).

Если скорость передачи сообщений меньше пропускной способности канала связи,

то существуют коды и методы декодирования такие, что средняя и максимальная вероятности ошибки декодирования стремятся к нулю, когда длина блока стремится к бесконечности,

C \,» style=»max-width : 98%; height: auto; width: auto;» src=»http://dic.academic.ru/pictures/wiki/files/48/06361f1e73691ae593c595b5dc19371f.png» border=»0″ />

то тогда, на основе которого можно добиться сколько угодной малой вероятности возникновения ошибки, не существует.

Теорема Шеннона-Хартли

В данной теореме определено, что достичь максимальной скорости (бит/сек) можно путем увеличения полосы пропускания и мощности сигнала и, в то же время, уменьшения шума.

Теорема Шеннона-Хартли ограничивает информационную скорость (бит/с) для заданной полосы пропускания и отношения сигнал/шум. Для увеличения скорости необходимо увеличить уровень полезного сигнала, по отношению к уровню шума.

Значение теоремы

Сравнение способности Шеннона к законному Сравнению Хартли

способности канала к информационной норме из закона Хартли, мы можем найти эффективное число различимых уровней

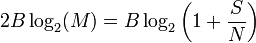
квадратный корень эффективно преобразовывает отношение мощности в отношение напряжения, таким образом число уровней приблизительно пропорционально отношению среднеквадратической амплитуды сигнала к шумовому стандартному отклонению. Это подобие в форме между способностью Шаннона и законом Hartley’s не должно интерпретироваться, чтобы означать, что М. уровней пульса можно буквально послать без любого беспорядка; больше уровней необходимо, чтобы учесть избыточное кодирование и устранение ошибки, но чистая скорость передачи данных, к которой можно приблизиться с кодированием, эквивалентна использованию того М. в законе Хартли.

Источник

Информационная теория

Обработка информации — важная техническая задача, чем, например, преобразование энергии из одной формы в другую. Важнейшим шагом в развитии теории информации стала работа Клода Шеннона (1948). Логарифмическое измерение количества данных было первоначальной теорией, и прикладными задачами по коммуникации в 1928 году. Наиболее известным является вероятностный подход к измерению информации, на основе которого представлен широкий раздел количественной теории.

Отличительная черта вероятностного подхода от комбинаторного состоит в том, что новые предположения об относительной занятости любой системы в разных состояниях и общего количества элементов не учитываются. Ряд информации взят из отсутствия неопределённости в выборе различных возможностей. В основе такого подхода лежат энтропийные и вероятностные множества.

Основная теорема Шеннона о кодировании

Важный практический вопрос при обработке информации — какова мощность системы передачи данных. Можно получить определённый ответ, используя уравнение Шеннона. Оно позволяет точно понять информационную пропускную способность любого сигнального канала. Формула Шеннона в информатике: I = — (p1log2 p1 + p2 log2 p2 +. + pN log2 pN)

Основная теория Шеннона о кодировании для дискретного канала с помехой, приведённая здесь без доказательства, аналогична теореме канала не имеющего помех: если источник данных с энтропией H (Z), а канал связи имеет ширину полосы C, то сообщения, сгенерированные источником, всегда могут быть закодированы так, чтобы их скорость передачи vz была произвольно близка к значению: vzm = C | H (Z).

Не существует метода кодирования, который бы позволял передавать со скоростью, превышающей vzm, и с произвольно низкой вероятностью ошибки. Другими словами, если поток информации: H ‘(Z) = vz * H (Z) C он не существует.

Стоит рассмотреть сигнал, который эффективно передаётся (т. е. без избыточности) в виде зависящего от времени аналогового напряжения. Картина изменения в течение определённого интервала T позволяет приёмнику выявить, какое из возможных сообщений было фактически отправлено.

Используя идею межсимвольного влияния, можно сказать, что, поскольку нет избыточности значения будут независимыми при условии, и они достаточно далеки друг от друга, чтобы их стоило отбирать отдельно. По сути, невозможно сказать, что одно из значений просто от знания другого. Конечно, для любого сообщения оба типа данных заранее определяются содержанием.

Но получатель не может знать, какое из всех возможных сообщений прибыло, пока оно не пришло. Если приёмник заранее знает, какое напряжение, должно быть, передано, то само сообщение не дало бы никакой новой информации! То есть получатель не будет знать больше после его прибытия, чем раньше.

Это приводит к замечательному выводу:

Именно поэтому случайный шум может привести к ошибкам в полученном сообщении. Статистические свойства эффективного сигнала аналогичны. Если шум был явно разным, приёмник мог легко отделить информацию и избежать каких-либо неполадок. Поэтому для обнаружения и исправления ошибок нужно сделать реальный сигнал менее «шумоподобным».

Условие применения формулы Шеннона — избыточность, создаёт предсказуемые отношения между различными участками сигнального устройства. Хотя это снижает эффективность передачи информации в системе, но помогает отличать детали сигнала от случайного шума. Здесь обнаружена максимально возможная информационная пропускная способность системы. Поэтому нужно избегать избыточности и позволять сигналу иметь «непредсказуемые» качества, которые делают его статистически похожим на случайный шум.

Передача сигналов

Реальный сигнал должен иметь конечную мощность. Следовательно, для этого набора сообщений должен быть некоторый максимально возможный уровень мощности. Это значит что напряжение тока сигнала ограничено к некоторому ряду. Это также означает, что мгновенное напряжение сигнала, должно быть, ограничено и не выступает за пределы диапазона. Аналогичный аргумент должен быть верен и для шума. Поскольку предполагается, что система эффективна, можно ожидать, сигнал и шум будут иметь аналогичные статистические свойства.

Это означает:

При передаче сигналов в присутствии шума нужно стараться, чтобы сигнал был больше и свести к минимуму эффекты шума. Поэтому можно ожидать, что система передачи информации применится и обеспечит, чтобы для каждого типичного сообщения сила почти равнялось некоторому максимальному значению.

Это означает, что в такой системе, большинство сообщений будет одинаковый уровень мощности. В идеале каждое ИС должно иметь одинаковый, максимально возможный уровень мощности. На самом деле можно повернуть этот аргумент с ног на голову и сказать, что «типичны» только сообщения со средними силами, подобными этому максимуму. Те, что обладают гораздо более низкими способностями, необычны — то есть редки.

Определённое уравнение

Сигнал и шум не коррелированны, то есть они не связаны каким-либо образом, который позволит предсказать один из них. Суммарная мощность, получаемая при объединении этих некоррелированных ИС, по-видимому, случайно изменяющихся величин, задаётся.

Поскольку сигнал и шум статистически аналогичны, их комбинация будет иметь то же значение форм-фактора, что и сам сигнал или шум. Потому можно ожидать, что комбинированный сигнал и шум, как правило, будут ограничены диапазоном напряжения.

Стоит рассмотреть теперь разделение этого диапазона на полосы одинакового размера. (т. е. каждая из этих полос будет охватывать ИС.) Чтобы предоставить другую метку для каждой полосы, нужны символы или цифры. Поэтому всегда можно указать, какую полосу занимает уровень напряжения в любой момент с точки зрения B-разрядного двоичного числа. По сути, этот процесс является ещё одним способом описания того, что происходит, когда берут цифровые образцы с B-разрядным аналоговым преобразователем, работающим в общем диапазоне.

Нет никакого реального смысла в выборе значения, которое настолько велико. Это потому что шум кубика будет просто иметь тенденцию рандомизировать фактическое напряжение на эту сумму, делая любые дополнительные биты бессмысленными. В результате максимальное количество битов информации, которую можно получить относительно уровня в любой момент, будет определено.

Уравнение Шеннона может использовать:

При передаче информации некоторые параметры используемых сигналов могут приобретать случайный символ в канале связи, например, из-за многолучевого распространения радиоволн, гетеродинирующих сигналов. В результате амплитуда и начальная фаза данных являются случайными. Согласно статистической теории связи, эти особенности сигналов необходимы для их оптимальной обработки, они определяют как структуру приёмника, так и качество связи.

Хартли понимал информационное получение как подбор одного вида данных из набора равновероятного сообщения и определил объём, содержащейся ВС, как логарифм N. Выполняются примеры решения по формуле Хартли в информатике: N = mn.

Помехи разложения всегда присутствуют в границе любого реального сигнала. Однако, если их уровень настолько мал, что вероятность искажения практически равна нулю, можно условно предположить, что все сигналы передаются неискажёнными.

В этом случае средний объём информации, переносимой одним символом, можно считать расчётным: J (Z; Y) = Хапр (Z) — Хапест (Z) = Хапр (Y). Поскольку функция H (Y) = H (Z) и H (Y / Z) = 0, а индекс max = Hmax (Y) — максимальная энтропия источника класса сигнала, возникающая в результате распределения символов Y: p (y1) = p (y2) = … = p (ym) = 1 / My, т. е. Hmax (Y) = logaMy.

Следовательно, главная дискретная ширина полосы таблицы без информации о помехах в единицу времени равна: Cy = Vy • max = Vy • Hmax (Y) = Vy • logaMy или записываться Ck = Vk • logaMy. Где буква Mk — должно быть максимально возможное количество уровней, разрешённых для передачи по этому каналу (конечно, может обозначаться Mk = My).

Согласно теореме, метод кодирования онлайн, который может использоваться и позволяет:

Вероятностный подход к определению вычисления объёма информации — математический вывод формулы Шеннона не является удовлетворительным для метода оценки роли энтропии, отражения элементов системы и может не применяться. Как общий информатический объект невозможно допустить единый способ измерения и его правила.

Источник

СОДЕРЖАНИЕ

Формулировка теоремы

Историческое развитие

В конце 1920-х годов Гарри Найквист и Ральф Хартли разработали несколько фундаментальных идей, связанных с передачей информации, особенно в контексте телеграфа как системы связи. В то время эти концепции были мощными прорывами по отдельности, но они не были частью всеобъемлющей теории. В 1940-х годах Клод Шеннон разработал концепцию пропускной способности канала, частично основанную на идеях Найквиста и Хартли, а затем сформулировал полную теорию информации и ее передачи.

Ставка Найквиста

В 1927 году Найквист определил, что количество независимых импульсов, которые могут быть пропущены по телеграфному каналу за единицу времени, ограничено удвоенной шириной полосы канала. В символической записи

Закон Хартли

В 1928 году Хартли сформулировал способ количественной оценки информации и ее линейной скорости (также известной как скорость передачи данных R бит в секунду). Этот метод, позже известный как закон Хартли, стал важным предшественником более изощренного представления Шеннона о пропускной способности канала.

M знак равно 1 + А Δ V <\ Displaystyle M = 1 + > .

Принимая информацию за импульс в битах / импульсах за логарифм по основанию 2 числа различных сообщений M, которые могут быть отправлены, Хартли построил меру линейной скорости R как:

Концепция безошибочной пропускной способности ждала Клода Шеннона, который основывался на наблюдениях Хартли о логарифмической мере информации и наблюдениях Найквиста о влиянии ограничений пропускной способности.

Теорема кодирования канала с шумом и пропускная способность

Развитие теории информации Клодом Шенноном во время Второй мировой войны явилось следующим большим шагом в понимании того, какой объем информации может быть надежно передан через зашумленные каналы. Основываясь на фундаменте Хартли, теорема Шеннона о кодировании канала с шумом (1948) описывает максимально возможную эффективность методов исправления ошибок по сравнению с уровнями шумовых помех и искажения данных. Доказательство теоремы показывает, что случайно построенный код с исправлением ошибок по существу не хуже наилучшего из возможных; Теорема доказывается с помощью статистики таких случайных кодов.

Обратное тоже важно. Если

вероятность ошибки на приемнике неограниченно возрастает с увеличением скорости. Таким образом, никакая полезная информация не может передаваться за пределы пропускной способности канала. Теорема не рассматривает редкую ситуацию, в которой скорость и мощность равны.

Если бы существовала такая вещь, как аналоговый канал без шума, можно было бы передавать по нему неограниченное количество безошибочных данных за единицу времени (обратите внимание, что аналоговый канал с бесконечной полосой пропускания не может передавать неограниченное количество безошибочных данных. отсутствует бесконечная мощность сигнала). Однако реальные каналы подвержены ограничениям, налагаемым как конечной полосой пропускания, так и ненулевым шумом.

В канале, рассматриваемом теоремой Шеннона – Хартли, шум и сигнал суммируются. То есть приемник измеряет сигнал, который равен сумме сигнала, кодирующего желаемую информацию, и непрерывной случайной величины, представляющей шум. Это добавление создает неопределенность относительно значения исходного сигнала. Если приемник имеет некоторую информацию о случайном процессе, который генерирует шум, в принципе можно восстановить информацию в исходном сигнале, рассматривая все возможные состояния шумового процесса. В случае теоремы Шеннона – Хартли предполагается, что шум генерируется гауссовским процессом с известной дисперсией. Поскольку дисперсия гауссовского процесса эквивалентна его мощности, принято называть эту дисперсию мощностью шума.

Такой канал называется каналом аддитивного белого гауссова шума, потому что к сигналу добавляется гауссов шум; «белый» означает равное количество шума на всех частотах в полосе пропускания канала. Такой шум может возникать как из-за случайных источников энергии, так и из-за ошибок кодирования и измерения на отправителе и получателе соответственно. Поскольку суммы независимых гауссовских случайных величин сами являются гауссовскими случайными величинами, это удобно упрощает анализ, если предположить, что такие источники ошибок также являются гауссовыми и независимыми.

Следствия теоремы

Сравнение способности Шеннона с законом Хартли

Сравнивая пропускную способность канала со скоростью передачи информации по закону Хартли, мы можем найти эффективное количество различимых уровней M :

Квадратный корень эффективно преобразует отношение мощностей обратно в отношение напряжений, поэтому количество уровней приблизительно пропорционально отношению среднеквадратичной амплитуды сигнала к стандартному отклонению шума.

Частотно-зависимый (цветной шум) случай

Приближения

Для больших или малых и постоянных отношений сигнал / шум формула емкости может быть приближена:

Случай с ограниченной пропускной способностью

Когда отношение сигнал / шум велико ( S / N 1 ), логарифм аппроксимируется следующим образом:

C ≈ 0,332 ⋅ B ⋅ S N р ( я п d B ) <\ Displaystyle С \ приблизительно 0,332 \ CDOT B \ CDOT \ mathrm >

Корпус с ограничением мощности

Источник