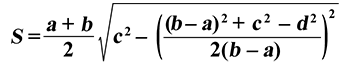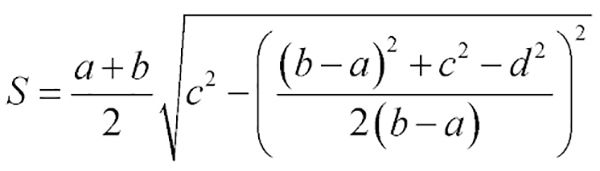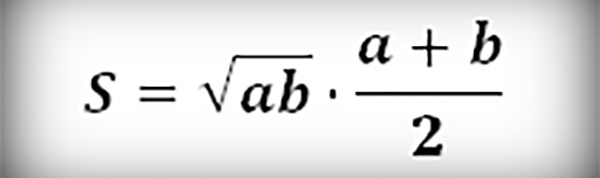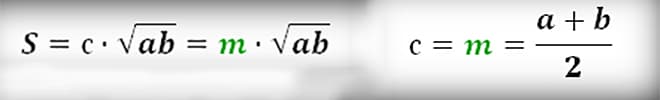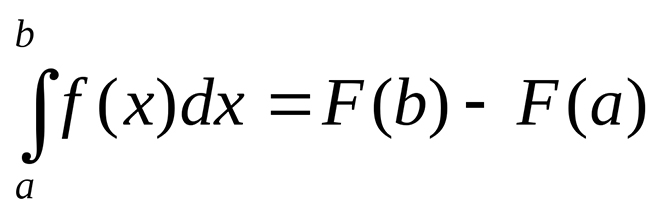площадь трапеции можно вычислить по формуле
Площадь трапеции можно вычислить по формуле
Площадь трапеции можно вычислить по формуле
, где
— основания трапеции,
— высота (в метрах). Пользуясь этой формулой, найдите высоту
, если основания трапеции равны
и
, а её площадь
.
Выразим высоту трапеции из формулы площади:
Приведём другое решение.
Подставим в формулу известные значения величин:
Площадь трапеции можно вычислить по формуле
Площадь трапеции можно вычислить по формуле
где
— основания трапеции,
— высота (в метрах). Пользуясь этой формулой, найдите высоту
если основания трапеции равны
и
а её площадь
Выразим высоту трапеции из формулы площади:
Приведём другое решение.
Подставим в формулу известные значения величин:
Площадь трапеции
Онлайн калькулятор
Через длины оснований и высоту

основание a =
основание b =
высота h =
Чему равна площадь трапеции если известны основания a и b, а также высота h?
Формула
Пример
Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:
S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²
Через среднюю линию и высоту
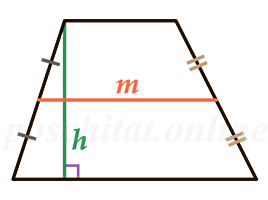
средняя линия m =
высота h =
Чему равна площадь трапеции если известны средняя линия m и высота h?
Формула
Пример
Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:
Через длины сторон и оснований
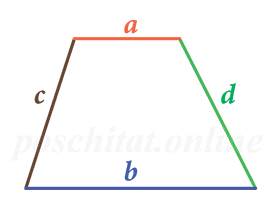
основание a =
основание b =
сторона c = сторона d =
Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?
Формула
Пример
Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:
Через диагонали и угол между ними
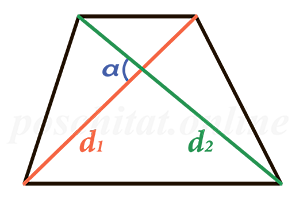
Чему равна площадь трапеции если известны диагонали d1 и d2 и угол между ними α?
Формула
Пример
Если у трапеции одна диагональ d1 = 5 см, другая диагональ d2 = 7 см, а угол между ними ∠α = 30°, то её площадь:
S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.5 ⋅ 0.5= 8.75 см²
Площадь равнобедренной трапеции
Через среднюю линию, боковую сторону и угол при основании
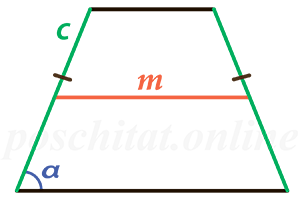
средняя линия m =
сторона c =
угол α =
Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?
Формула
Пример
Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:
S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²
Через радиус вписанной окружности
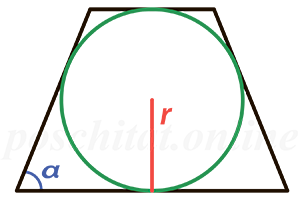
Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании α?
Формула
Пример
Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:
S = 4 ⋅ 5² / sin (30) = 100 / 0.5 = 200 см²
Трапеция
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a – h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a – c· cos α – d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
Средняя линия трапеции
Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
Через длины оснований и высоту
Чему равна площадь трапеции если известны основания a и b, а также высота h?
Формула
Пример
Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:
S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²
Площадь трапеции через перпендикулярные диагонали
Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
Таблица с формулами площади трапеции
В зависимости от известных исходных данных и вида трапеции, площадь трапеции можно вычислить по различным формулам.
| эскиз | формула | ||
| Площадь для всех видов трапеции | |||
| 1 | высота и два основания |  | |
| 2 | высота и средняя линия |  | |
| 3 | четыре стороны |  | |
| 4 | диагонали и угол между ними |  | |
| 5 | основания и углы при одном из оснований |  | |
| Площадь равнобедренной трапеции | |||
| 6 | стороны |  | |
| 7 | основание, боковые стороны и угол при основании |  | |
| 8 | основание, боковые стороны и угол при основании |  | |
| 9 | основания и углы при одном из оснований |  | |
| 10 | диагонали и угол между ними |  | |
| 11 | средняя линия, боковые стороны и углы между основанием и боковыми сторонами |  | |
| 12 | радиус вписанной окружности и угол при основании |  | |
| 13 | основания и радиус вписанной окружности |  | |
| 14 | основания и углы при одном из оснований |  | |
| 15 | основания и боковые стороны |  | |
| 16 | основания и средняя линия |  | |
Найти площадь равнобедренной трапеции, зная радиус вписанной окружности и угол
Через среднюю линию, боковую сторону и угол при основании
Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Пусть a и b основания трапеции. доказать что отрезок, соединяющий середины её диагоналей равен 1/2 * | а – б|?
Возьмем трапецию ABCD
Определим точку М как середину диагонали АС, точку N как середину диагонали BD. Тогда средняя линия трапеции KF будет проходить через точки M и N.
Вспомним свойство средней линии трапеции: средняя линия трапеции является параллельной основаниям и равняется полусумме их длин.
Рассмотрим треугольник ACD:
Рассмотрим треугольник BCD
Выразим MN через отрезки MF и NF:
Подставим в формулу значения отрезков MF и NF:
Площадь трапеции через основания и два угла
Площадь трапеции: как вычислить, формула
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
т.е. взять полусумму оснований, умноженную на высоту.
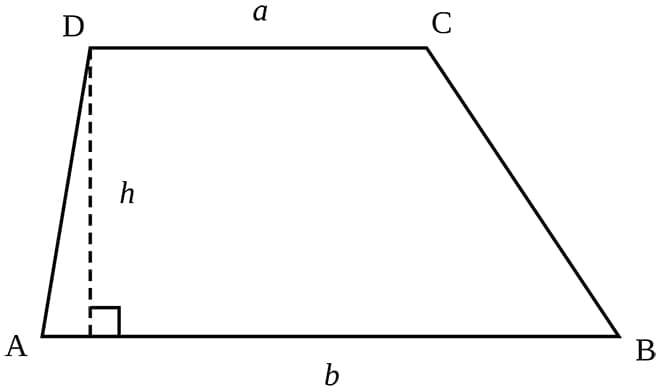
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.

Найти площадь равнобедренной трапеции можно несколькими способами.
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
S = c * sin α * (b – c * cos α)
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
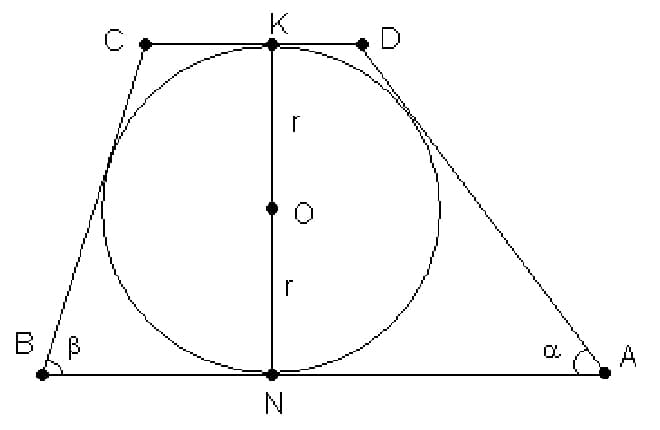
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
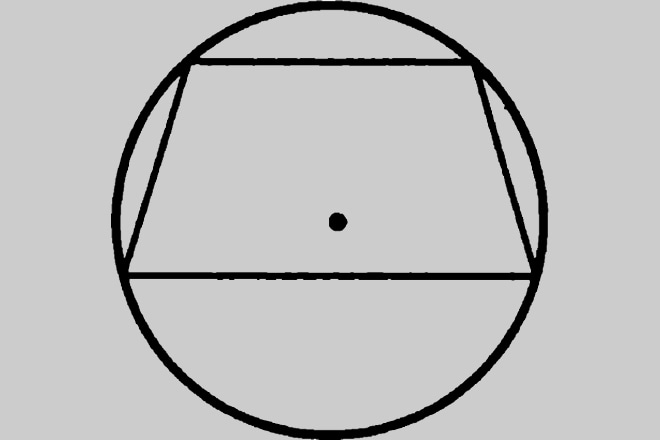
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
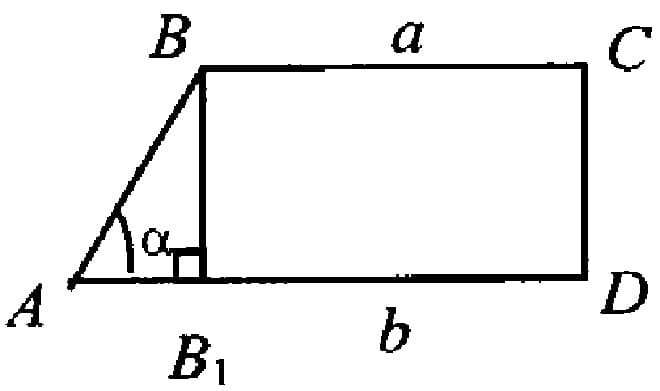
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
или на длину боковой перпендикулярной стороны:
S = ½ * d1 * d2 * sin α
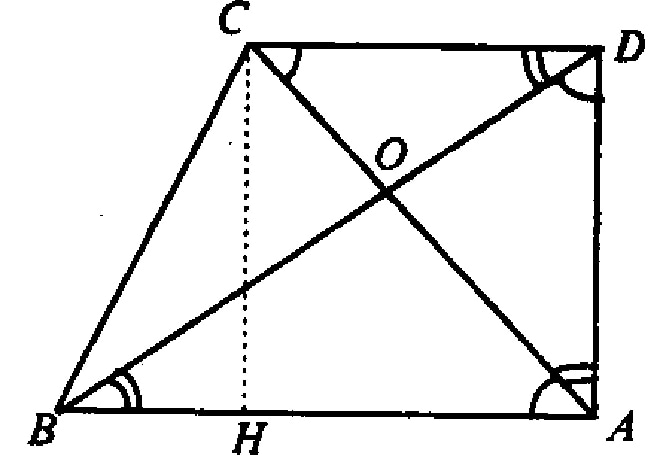
Если диагонали перпендикулярны, то формула упрощается до:
Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке [a;b], осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
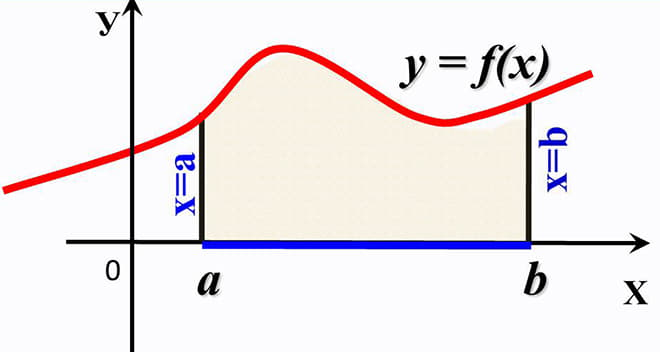
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.