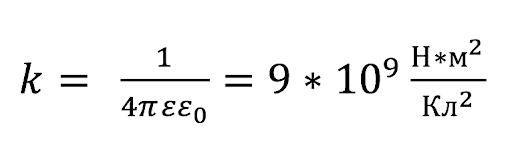какое выражение является законом сохранения электрического заряда

Закон сохранения электрического заряда.

Закон сохранения электрического заряда гласит, что алгебраическая сумма электрических зарядов всех частиц изолированной системы не меняется при происходящих в ней процессах.

Электрический заряд любой частицы или системы частиц является целым кратным элементарному электрическому заряду (равному по величине заряду электрона) или нулевым.

Закон сохранения заряда подтверждается и простыми опытами по электризации тел. Укрепим на стержне электромера металлический диск и, положив на него прослойку из сукна, поставим сверху еще один такой же диск, но с ручкой из диэлектрика. Совершив несколько движений верхним диском по изоляционной прослойке, уберем его в сторону. Мы увидим, что стрелка электромера отклонится, свидетельствуя о появлении на сукне и соприкасающемся с ним диске электрического заряда. Далее прикоснемся вторым диском (которым мы терли о сукно) к стерж­ню второго электромера. Стрелка этого электромера отклонится примерно на такой же угол, что и стрелка первого электромера. Это означает, что при электризации оба диска получили одинако­вый по модулю заряд. Что можно сказать о знаках этих зарядов? Для ответа на этот вопрос завер­шим опыт, соединив электромеры металлическим стержнем. Мы увидим, как стрелки приборов опустятся вниз. Нейтрализация зарядов свидетельствует о том, что они были равны по модулю, но противоположны по знаку (и, следовательно, в сумме давали нуль).

Этот и другие опыты показывают, что в процессе электризации общий (суммарный) заряд тел сохраняется: если он был равен нулю до электризации, то таким он останется и после нее.

Полный электрический заряд сохраняется и в том случае, если первоначальные заряды тел были отличны от нуля. Если обозначить первоначальные заряды тел как q₁ и q₂, а заряд тех же тел после их взаимодействия как q’₁ и q’₂ то можно записать:

При любых взаимодействиях тел их полный электрический заряд остается неизменным.

В этом заключается фундаментальный закон природы — закон сохранения электрического заряда.

Закон сохранения заряда был установлен в 1750 г. американским ученым и видным политическим деятелем Бенджамином Франклином. Он же ввел понятие о положительных и отрицатель­ных зарядах, обозначив их знаками «+» и «-».

Закон сохранения заряда имеет глубокий смысл. Он очевиден, когда число элементарных частиц не меняется. Однако элементарные частицы могут возникать (рождаться) и исчезать, т. е. пре­терпевать различные превращения. Возникают и исчезают элементарные частицы всегда пара­ми (с противоположными зарядами). Многочисленные наблюдения превращений элементарных частиц подтверждают закон сохранения заряда. Этот закон выражает одно из фундаментальных свойств электрического заряда.

Таким образом, электрический заряд во Вселенной сохраняется, а полный электрический за­ряд Вселенной, скорее всего, равен нулю.

Источник

Закон сохранения электрического заряда

Электрический заряд

Электрический заряд — это физическая величина, которая определяет способность тел создавать электромагнитное поле и принимать участие в электромагнитном взаимодействии.

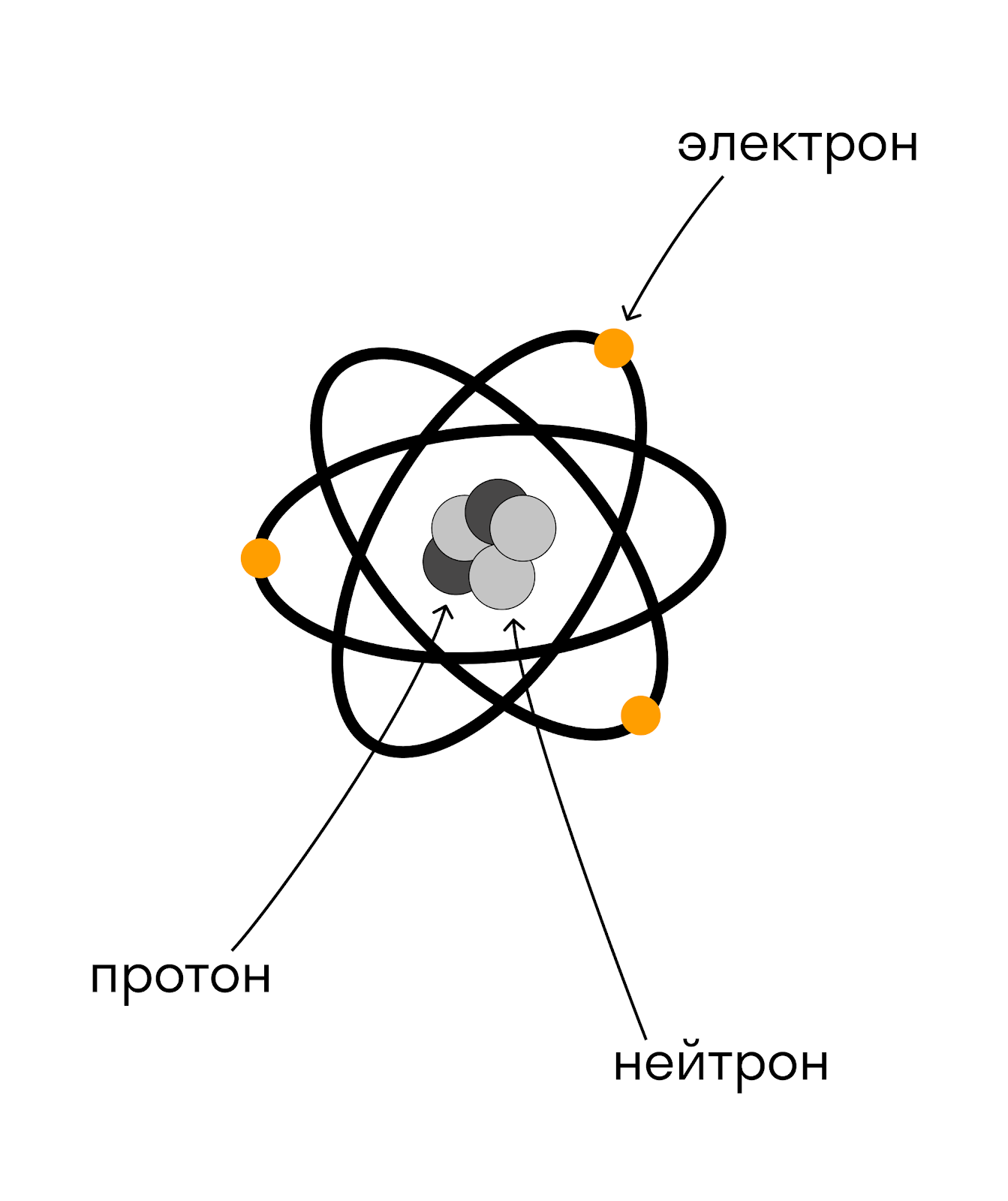
Мы состоим из клеток, клетки состоят из молекул, молекулы в свою очередь состоят из атомов, а атомы — из ядра и электронов. Ядро состоит из протонов и нейтронов.

Протон — это частица, которая заряжена положительно, нейтрон — нейтрально, а электрон — отрицательно. Электрон вращается по орбитам, которые во много раз больше, чем размер электрона.

Размер электрона с размером орбиты можно сравнить так: представьте футбольный мяч и футбольное поле. Во сколько раз поле больше мяча, во столько же раз орбита больше, чем электрон.

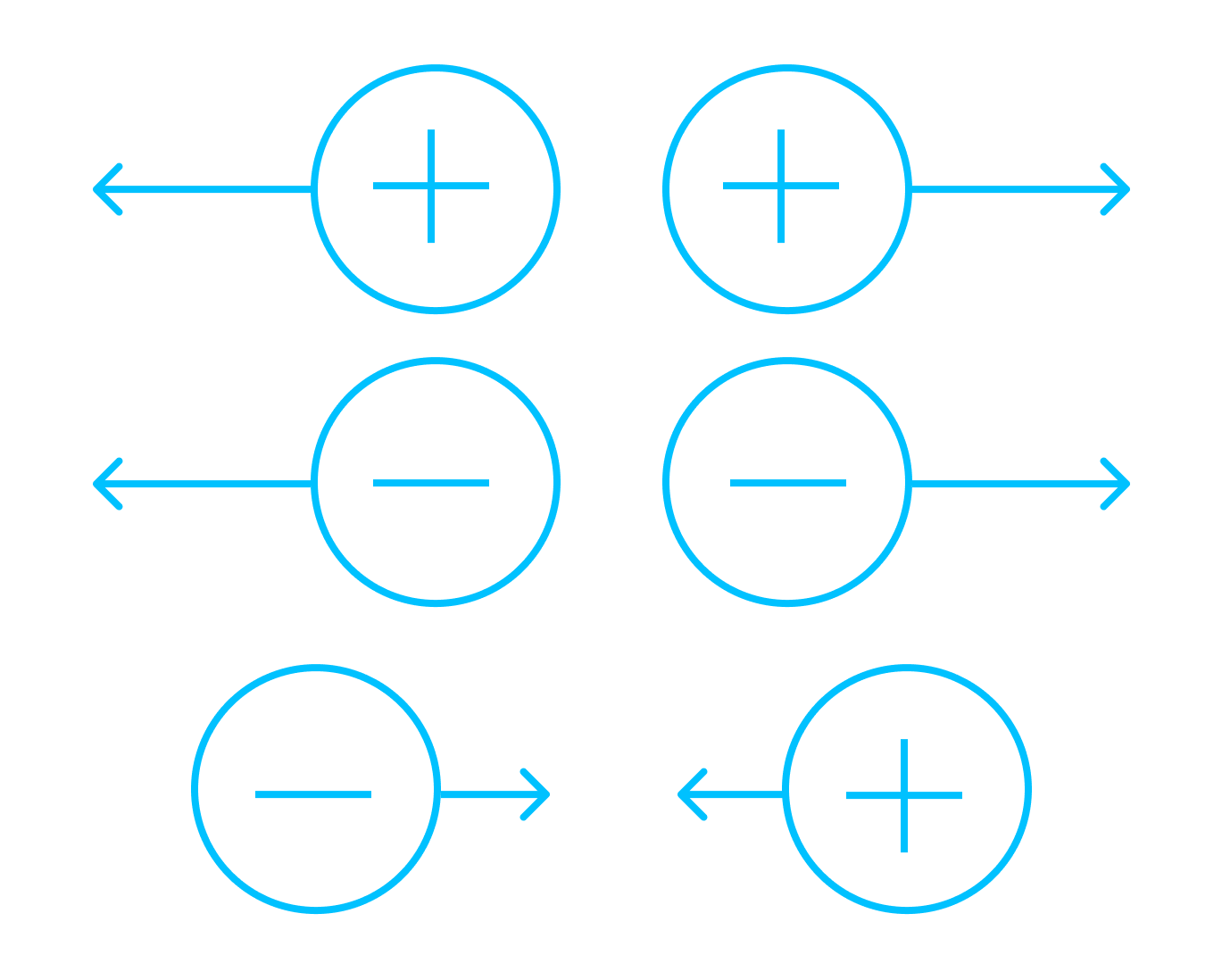
Как мы уже выяснили, электрические заряды бывают положительными и отрицательными. Одноименные заряды отталкиваются, разноименные притягиваются:

А вот измерять Электрический заряд мы будем в Кулонах [Кл]. Нет, не тех, что болтаются на цепочке. Шарль Кулон — это физик, который изучал электромагнитные явления.

Электризация

Чтобы разобраться с тем, как тело приобретает электрический заряд и сохраняет его, нам для начала нужно поближе познакомится с протоном и электроном. Протон — ленивый и неповоротливый — он точно не будет никуда перемещаться, если мы не переместим атом целиком.

А вот электрон — парень подвижный, и ему перебежать с одного атома на другой — ничего не стоит.

Мы поговорим о двух типах электризации: электризация соприкосновением и электризация трением.

Свободные электроны переходят с незаряженного тела на нейтральное. А если мы возьмем положительно заряженное тело вместо отрицательного, то свободные электроны перейдут с нейтрального тела, чтобы уравновесить заряды.

Электроны переходят от одного тела к другому и в отличии от электризации соприкосновением заряжаются противоположными по знаку и равными по модулю зарядами.

То есть при соприкосновении заряд раздают одного знака и поровну. Как если бы ты поделился с другом конфетами, которых у тебя с избытком.

При трении наоборот — заряды у тел будут разных знаков, но также в одинаковом количестве. Например, у вас есть равное количество денег в рублях и долларах, и у меня аналогичная ситуация с той же суммой. Вы решили лететь в США, а мне как раз доллары не нужны. Чтобы не ходить в банк, мы можем просто поменяться. Тогда у вас будут только доллары, а у меня — только рубли. Главное, договориться про курс 🙂

Давайте решим пару задач по этой теме.

Задачка один

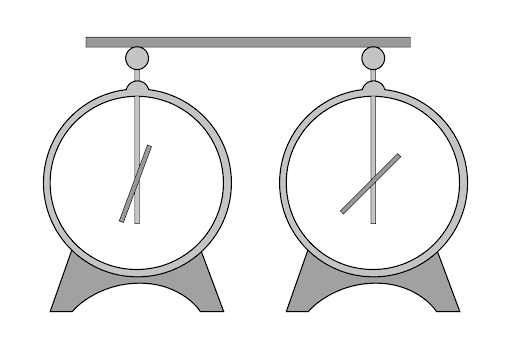
Из какого материала может быть сделан стержень, соединяющий электрометры, изображённые на рисунке?

Решение:

Он может быть сделан либо из проводника, либо из диэлектрика. Проводник пропускает через себя заряды, а диэлектрик — нет. Если мы посмотрим на показания электрометров, то увидим, что они отличаются.

Как мы помним, при соприкосновении заряды уравниваются по величине (один электрометр делится конфетами с другим). В данном случае никто ни с кем не делился, это значит, что стержень не пропускает — он диэлектрик. И стекло, и эбонит являются диэлектриками. Значит подходят оба варианта!

Задачка два

В процессе трения о шёлк стеклянная линейка приобрела положительный заряд. Как при этом изменилось количество заряженных частиц на линейке и шёлке при условии, что обмен при трении не происходил?

А) количество протонов на стеклянной линейке

Б) количество электронов на шёлке

Решение:

Вспомните, как мы охарактеризовали протон: он ленивый и неподвижный! Значит количество протонов ни на стеклянной линейке, ни на шелке измениться просто не может. Мы же не отламываем кусок линейки вместе с атомами, из которых она состоит. А вот электроны охотно перемещаются. Нам известно, что линейка приобрела положительный заряд. Получается, электроны сбежали от нее к шелку. Следовательно, количество электронов на шелке увеличилось.

Электростатическая индукция

Кажется, с электризацией разобрались. Теперь разберемся, что произойдет, если мы поднесем одно тело к другому, но не вплотную. Произойдет такое явление, как электростатическая индукция — явление перераспределения зарядов в нейтрально заряженных телах.

Давай разбираться на примере задачи:

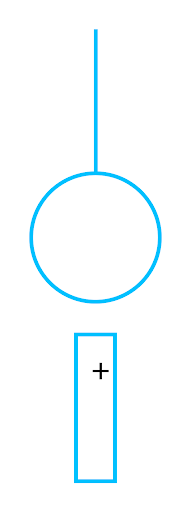
На нити подвешен незаряженный металлический шарик. К нему снизу поднесли положительно заряженную палочку. Как изменится при этом сила натяжения нити?

Решение:

Здесь важно подчеркнуть, что незаряженный — значит заряжен нейтрально. То есть в теле равное количество положительных и отрицательных зарядов.

Электроны металлического шарика будут притягиваться к поднесенной положительной палочке. В результате шарик притягивается к палочке, следовательно, сила натяжения нити увеличивается.

Ответ: сила натяжения нити увеличивается

Поляризация диэлектрика

Давайте возьмем два, на первый взгляд, одинаковых задания из ЕГЭ.

Задание 1

Если к незаряженному металлическому шару поднести, не касаясь, точечный положительный заряд, то на стороне шара, ближайшей к заряду, появится отрицательный заряд. Как называется это явление?

Мы только что это разобрали: то электростатическая индукция.

Задание 2

Если к незаряженному диэлектрическому шару поднести, не касаясь, точечный положительный заряд, то на стороне шара, ближайшей к заряду, появится отрицательный заряд. Как называется это явление?

Кажется, что очень похоже на электростатическую индукцию, но это явление будет называться поляризация. В чем разница:

В первом случае — это проводник, а во втором — диэлектрик. Если не вдаваться в подробности, то поляризация диэлектрика — процесс, очень похожий по природе своей на электростатическую индукцию, только происходит в непроводящих материалах.

Закон сохранения электрического заряда

И последнее, о чем мы сегодня поговорим — этот закон сохранения заряда

Алгебраическая сумма зарядов электрически замкнутой системы сохраняется.

Закон сохранения заряда

q1 + q2 + q3 + … + qn = const

q1, q2, q3, …, qn — заряды электрически замкнутой системы [Кл]

Задачка раз

Решение:

Для решения этой задачи нам нужно найти алгебраическую сумму зарядов.

Это суммарный заряд шариков и до, и после и во время взаимодействия.

Так как суммарный заряд сохраняется, но шарики соприкоснулись, суммарный заряд разделится между всеми шариками поровну. То есть нам нужно суммарный заряд просто поделить на количество шариков — на 2.

И это ответ к нашей задаче.

Задачка два

Металлическая пластина, имевшая положительный заряд, по модулю равный 10е, при освещении потеряла шесть электронов. Каким стал заряд пластины?

Решение:

q = q₀ — 6(— e) = 10e + 6e = 16e

Красный знак «минус» образуется из-за того, что мы «отнимаем» электроны, а зеленый — из-за того, что электрон отрицательный. «Минус на минус» дает плюс, поэтому мы получаем 10e + 6e = 16е.

Ответ: 16е

Задачка три

Решение:

По закону сохранения заряда сумма зарядов в замкнутой системе остается постоянной.

Два шарика привели в соприкосновение и развели, значит их суммарный заряд разделится между шариками поровну.

Ответ: заряды шариков равны 2q.

Закон Кулона и связь с гравитацией

Мы уже упоминали Шарля Кулона. В честь него названа единица измерения заряда — Кулон. Он придумал закон о взаимодействии зарядом.

Закон Кулона

k — коэффициент пропорциональности

E₀= 8,85 * 10-12Н*м²/Кл² — электрическая постоянная

E — диэлектрическая проницаемость среды — показывает во сколько раз сила электростатического взаимодействия в вакууме больше силы в среде (в вакууме равна 1)

q1 — заряд первого тела [Кл]

q2 — заряд второго тела [Кл]

r — расстояние между телами [м]

F — сила электростатического взаимодействия (кулоновская) [Н]

Мы уже знаем, что заряды бывают положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные — притягиваются. Это значит, что сила направлена туда же, куда заряд будет стремиться двигаться.

Например, у положительного заряда сила будет направлена в сторону отрицательного, если он есть где-то поблизости, и от положительного, так как одноименные заряды отталкиваются.

Согласно третьему закону Ньютона, силы одной природы возникают попарно, равны по величине, противоположны по направлению. Если взаимодействуют два неодинаковых заряда, сила, с которой больший заряд действует на меньший (В на А) равна силе, с которой меньший действует на больший (А на В).

Интересно, что у различных законов физики есть некоторые общие черты. Вспомним закон тяготения. Сила гравитации также обратно пропорциональны квадрату расстояния, но уже между массами. И невольно возникает мысль, что в этой закономерности таится глубокий смысл. До сих пор никому не удалось представить тяготение и электричество, как два разных проявления одной и той же сущности.

Сила и тут изменяется обратно пропорционально квадрату расстояния, но разница в величине электрических сил и сил тяготения поразительна. Пытаясь установить общую природу тяготения и электричества, мы обнаруживаем такое превосходство электрических сил над силами тяготения, что трудно поверить, будто у тех и у других один и тот же источник. Нельзя говорить, что одно действует сильнее другого, ведь все зависит от того, какова масса и каков заряд.

Рассуждая о том, насколько сильно действует тяготение, мы не вправе говорить: «Возьмем массу такой-то величины», потому что мы выбираем ее сами. Но если мы возьмем то, что предлагает нам сама Природа: ее собственные числа и меры, которые не имеют ничего общего с нашими дюймами, годами — с любыми нашими мерами, вот тогда мы можем сравнивать.

Мы возьмем элементарную заряженную частицу, например, электрон. Две элементарные частицы, два электрона, за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.

Закон Всемирного тяготения

G= 6,67 * 10⁻¹¹*11м³/кг*c² — гравитационная постоянная

m1 — масса первого тела [кг]

m2 — масса второго тела [кг]

r — расстояние между телами [м]

F — сила гравитационного притяжения [Н]

Тяготение относится к электрическому отталкиванию, как единица к числу с 42 нулями. Да, это огромное число! Исследователи перебирали все большие числа, чтобы понять — откуда это взялось. Одно из таких больших чисел — это отношение диаметра Вселенной к диаметру протона — как ни удивительно, это тоже число с 42 нулями. Нормально так перебрали.

Если вы смотрели Рика и Морти, то знаете о теории параллельных вселенных и о том, что эти вселенные расширяются. Из-за расширения вселенной постоянная сила тяготения меняется. Хотя эта гипотеза еще не опровергнута, у нас нет никаких свидетельств в ее пользу. Наоборот, некоторые данные говорят о том, что постоянная сила тяготения не менялась таким образом. Это громадное число по сей день остается загадкой.

От расширяющихся вселенных и мультиков перейдем к чему-то более приземленному — к задачам.

Задачка раз

Расстояние между двумя точечными электрическими зарядами уменьшили в 3 раза, каждый из зарядов увеличили в 3 раза. Во сколько раз увеличился модуль сил электростатического взаимодействия между ними?

Решение:

Возьмем закон Кулона.

Если расстояние уменьшилось в 3 раза, то знаменатель уменьшился в 9 раз. Каждый из зарядов увеличился в три раза, значит числитель увеличился в 9 раз. Уменьшаем знаменатель в 9 раз, тем самым увеличивая всю дробь в 9 раз, увеличиваем числитель в 9 раз, получаем, что вся дробь увеличилась в 81 раз. И это ответ.

Ответ: модуль сил электростатического взаимодействия увеличится в 81 раз.

Задачка два (последняя!)

Два одинаковых маленьких отрицательно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 5 раз.

Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₂ к F₁.

Решение:

Для начала найдем заряд шариков после соприкосновения.

Теперь по закону кулона найдем силу F2

И находим отношение сил

Ответ: отношение сил равно 1,8

Источник

Физика. 10 класс

§ 16. Электрический заряд. Закон сохранения электрического заряда

Что означает наличие электрического заряда у тела или частицы? Как взаимодействуют электрически заряженные тела?

Электрический заряд. О том, что янтарь, потёртый о шерсть, приобретает свойство притягивать лёгкие предметы (рис. 94), знали ещё древние греки. Однако только в 1600 г. лейб-медик королевы Англии доктор медицины Уильям Гильберт в книге «О магните, магнитных телах и большом магните — Земле» дал первое систематизированное описание свойств электрических и магнитных материалов. Гильберт продемонстрировал, что кроме янтаря свойством притягивать лёгкие предметы обладают после натирания алмаз, сера, фарфор и многие другие тела. Он назвал их «электрическими» (ελεκτρον по-гречески — янтарь). Теперь мы говорим, что такие тела электрически заряжены, т. е. им сообщён электрический заряд.

Электрический заряд — физическая скалярная величина, характеризующая интенсивность электромагнитного взаимодействия тел (частиц).

Электрический заряд является источником электромагнитного поля, связанного с материальным носителем (телом или частицей). Электрический заряд, как и масса, не существует без тела или частицы.

Электрическим зарядам присущи следующие фундаментальные свойства:

1) электрические заряды существуют в двух видах, которые названы положительными и отрицательными (существование двух видов зарядов установил Шарль Дюфэ ( 1698‒1739 ) в 1733 г., а в 1747 г. Бенджамин Франклин ( 1706‒1790 ) приписал им знаки «+» и «‒»);

2) электрический заряд аддитивен, т. е. заряд любой системы тел (частиц) равен сумме зарядов тел (частиц), входящих в систему;

3) в любой электрически изолированной системе алгебраическая сумма зарядов тел (частиц) не изменяется;

4) электрический заряд дискретен, т. е. электрический заряд любого тела (частицы) кратен элементарному электрическому заряду;

5) значение электрического заряда тела (частицы) не зависит от выбора системы отсчёта, следовательно, не зависит от того, движется оно (она) или покоится;

6) электрический заряд тела (частицы) не зависит ни от его (её) механического состояния, ни от каких-либо действующих на него (неё) сил.

Существуют два вида электрических зарядов, которые условились называть положительными и отрицательными. Причём при взаимодействии одноимённо заряженные тела (частицы) отталкивают друг друга (рис. 95, а), а разноимённо заряженные — притягивают друг друга (рис. 95, б).

Заряды разных тел (частиц) могут отличаться не только знаками, но и числовыми значениями.

За единицу электрического заряда в СИ принят кулон (Кл). Эта единица названа в честь Шарля Кулона (1736–1806). 1 Кл — величина электрического заряда, проходящего через поперечное сечение проводника за промежуток времени 1 с при силе постоянного тока 1 А.

Интересно знать

Один кулон — очень большая величина заряда. Расчёты показывают, что на удалённом от всех остальных тел металлическом шаре, находящемся в сухом воздухе, может находиться избыточный заряд 1 Кл, если его диаметр не менее 110 м. Вместе с тем при включении автомобильных фар сила тока в цепи приблизительно 10 А, т. е. ежесекундно через поперечное сечение проводников, подсоединённых к фарам, проходит заряд приблизительно 10 Кл.

Источник

Какое выражение является законом сохранения электрического заряда

Электрический заряд – это физическая величина, характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обычно обозначается буквами q или Q. В системе СИ электрический заряд измеряется в Кулонах (Кл). Свободный заряд в 1 Кл – это гигантская величина заряда, практически не встречающаяся в природе. Как правило, Вам придется иметь дело с микрокулонами (1 мкКл = 10 –6 Кл), нанокулонами (1 нКл = 10 –9 Кл) и пикокулонами (1 пКл = 10 –12 Кл). Электрический заряд обладает следующими свойствами:

1. Электрический заряд является видом материи.

2. Электрический заряд не зависит от движения частицы и от ее скорости.

3. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

4. Существует два рода электрических зарядов, условно названных положительными и отрицательными.

5. Все заряды взаимодействуют друг с другом. При этом одноименные заряды отталкиваются, разноименные – притягиваются. Силы взаимодействия зарядов являются центральными, то есть лежат на прямой, соединяющей центры зарядов.

6. Существует минимально возможный (по модулю) электрический заряд, называемый элементарным зарядом. Его значение:

e = 1,602177·10 –19 Кл ≈ 1,6·10 –19 Кл.

Электрический заряд любого тела всегда кратен элементарному заряду:

где: N – целое число. Обратите внимание, невозможно существование заряда, равного 0,5е; 1,7е; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.

7. Закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Из закона сохранения заряда так же следует, если два тела одного размера и формы, обладающие зарядами q 1 и q 2 (совершенно не важно какого знака заряды), привести в соприкосновение, а затем обратно развести, то заряд каждого из тел станет равным:

С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.

В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов, или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион. Обратите внимание, что положительные протоны входят в состав ядра атома, поэтому их число может изменяться только при ядерных реакциях. Очевидно, что при электризации тел ядерных реакций не происходит. Поэтому в любых электрических явлениях число протонов не меняется, изменяется только число электронов. Так, сообщение телу отрицательного заряда означает передачу ему лишних электронов. А сообщение положительного заряда, вопреки частой ошибке, означает не добавление протонов, а отнимание электронов. Заряд может передаваться от одного тела к другому только порциями, содержащими целое число электронов.

Иногда в задачах электрический заряд распределен по некоторому телу. Для описания этого распределения вводятся следующие величины:

1. Линейная плотность заряда. Используется для описания распределения заряда по нити:

где: L – длина нити. Измеряется в Кл/м.

2. Поверхностная плотность заряда. Используется для описания распределения заряда по поверхности тела:

3. Объемная плотность заряда. Используется для описания распределения заряда по объему тела:

Обратите внимание на то, что масса электрона равна:

Закон Кулона

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:

Силы взаимодействия точечных неподвижных зарядов подчиняются третьему закону Ньютона, и являются силами отталкивания друг от друга при одинаковых знаках зарядов и силами притяжения друг к другу при разных знаках. Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел, равномерно заряженных сфер и шаров. В этом случае за расстояния r берут расстояние между центрами сфер или шаров. На практике закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент k в системе СИ иногда записывают в виде:

где: ε 0 = 8,85∙10 –12 Ф/м – электрическая постоянная.

Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции: если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

Запомните также два важных определения:

Проводники – вещества, содержащие свободные носители электрического заряда. Внутри проводника возможно свободное движение электронов – носителей заряда (по проводникам может протекать электрический ток). К проводникам относятся металлы, растворы и расплавы электролитов, ионизированные газы, плазма.

Диэлектрики (изоляторы) – вещества, в которых нет свободных носителей заряда. Свободное движение электронов внутри диэлектриков невозможно (по ним не может протекать электрический ток). Именно диэлектрики обладают некоторой не равной единице диэлектрической проницаемостью ε.

Для диэлектрической проницаемости вещества верно следующее (о том, что такое электрическое поле чуть ниже):

Электрическое поле и его напряженность

По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда:

Напряженность электрического поля – векторная физическая величина. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.

Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии обладают следующими свойствами.

Электрическое поле называют однородным, если вектор напряжённости одинаков во всех точках поля. Например, однородное поле создаёт плоский конденсатор – две пластины, заряженные равным по величине и противоположным по знаку зарядом, разделённые слоем диэлектрика, причём расстояние между пластинами много меньше размеров пластин.

Во всех точках однородного поля на заряд q, внесённый в однородное поле с напряжённостью E, действует одинаковая по величине и направлению сила, равная F = Eq. Причём, если заряд q положительный, то направление силы совпадает с направлением вектора напряжённости, а если заряд отрицательный, то вектора силы и напряжённости противоположно направлены.

Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рисунке:

Принцип суперпозиции

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:

Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q > 0, то вектор напряженности направлен от заряда, если Q

Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:

Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:

Потенциальная энергия взаимодействия зарядов

Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывает потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:

Обратите внимание на отсутствие модулей у зарядов. Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.

Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.

Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью. Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.

Потенциал. Разность потенциалов. Напряжение

Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.

Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.

Принцип суперпозиции потенциала

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):

Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.

Электрическая емкость. Плоский конденсатор

При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:

В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.

Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:

За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0. Электроёмкость плоского конденсатора может быть рассчитана по формуле:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Обратите внимание, что S в этой формуле есть площадь только одной обкладки конденсатора. Когда в задаче говорят о «площади обкладок», то имеют в виду именно эту величину. На 2 умножать или делить её не надо никогда.

Еще раз приведем формулу для заряда конденсатора. Под зарядом конденсатора понимают только заряд его положительной обкладки:

Сила притяжения пластин конденсатора. Сила, действующая на каждую обкладку, определяется не полным полем конденсатора, а полем, созданным противоположной обкладкой (сама на себя обкладка не действует). Напряженность этого поля равна половине напряженности полного поля, и сила взаимодействия пластин:

Энергия конденсатора. Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):

Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.

Энергия электрического поля

Электрическую энергию следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):

Соединения конденсаторов

Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:

При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:

Из закона сохранения заряда следует, что заряды на соседних обкладках равны:

Напряжение равно сумме напряжений на отдельных конденсаторах.

Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:

Для N одинаковых последовательно соединённых конденсаторов:

Проводящая сфера

Напряженность поля внутри заряженного проводника равна нулю. В противном случае на свободные заряды внутри проводника действовала бы электрическая сила, которая вынуждала бы эти заряды двигаться внутри проводника. Это движение, в свою очередь, приводило бы к разогреванию заряженного проводника, чего на самом деле не происходит.

Факт того, что внутри проводника нет электрического поля можно понять и по-другому: если бы оно было то заряженные частицы опять таки двигались бы, причем они бы двигались именно так, чтобы свести это поле к нолю своим собственным полем, т.к. вообще-то двигаться им не хотелось бы, ведь всякая система стремится к равновесию. Рано или поздно все двигавшиеся заряды остановились бы именно в том месте, чтобы поле внутри проводника стало равно нолю.

На поверхности проводника напряжённость электрического поля максимальна. Величина напряжённости электрического поля заряженного шара за его пределами убывает по мере удаления от проводника и рассчитывается по формуле, аналогичной формулам для напряженности поля точечного заряда, в которой расстояния отсчитываются от центра шара.

Так как напряженность поля внутри заряженного проводника равна нулю, то потенциал во всех точках внутри и на поверхности проводника одинаков (только в этом случае разность потенциалов, а значит и напряжённость равна нулю). Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.

Электрическая емкость шара радиуса R:

Если шар окружен диэлектриком, то:

Свойства проводника в электрическом поле

Замечания к решению сложных задач

1. Заземление чего-либо означает соединение проводником данного объекта с Землей. При этом потенциалы Земли и имеющегося объекта выравниваются, а необходимые для этого заряды перебегают по проводнику с Земли на объект либо наоборот. При этом нужно учитывать несколько факторов, которые следуют из того, что Земля несоизмеримо больше любого объекта находящегося не ней:

2. Еще раз повторимся: расстояние между отталкивающимися телами минимально в тот момент, когда их скорости становятся равны по величине и направлены в одну сторону (относительная скорость зарядов равна нулю). В этот момент потенциальная энергия взаимодействия зарядов максимальна. Расстояние между притягивающимися телами максимально, также в момент равенства скоростей, направленных в одну сторону.

3. Если в задаче имеется система, состоящая из большого количества зарядов, то необходимо рассматривать и расписывать силы, действующие на заряд, который не находится в центре симметрии.

Источник