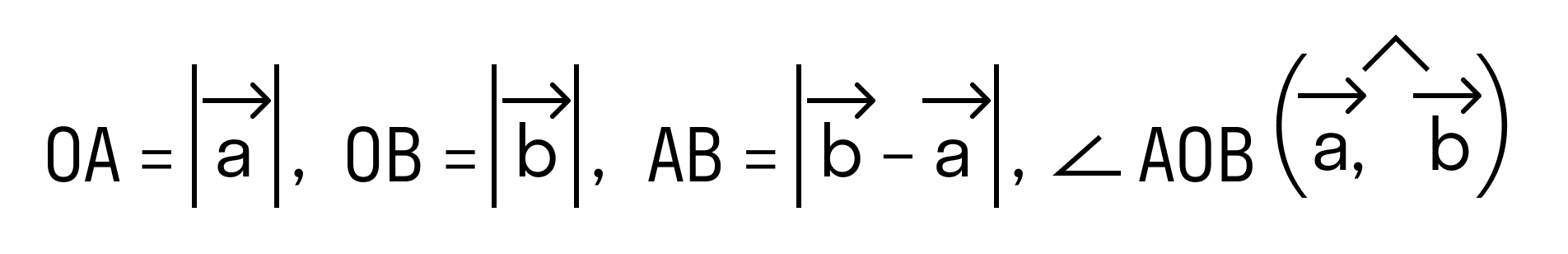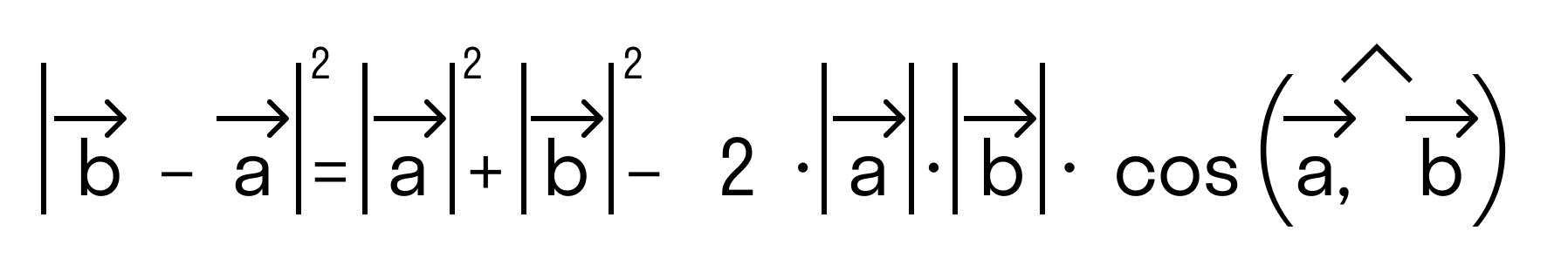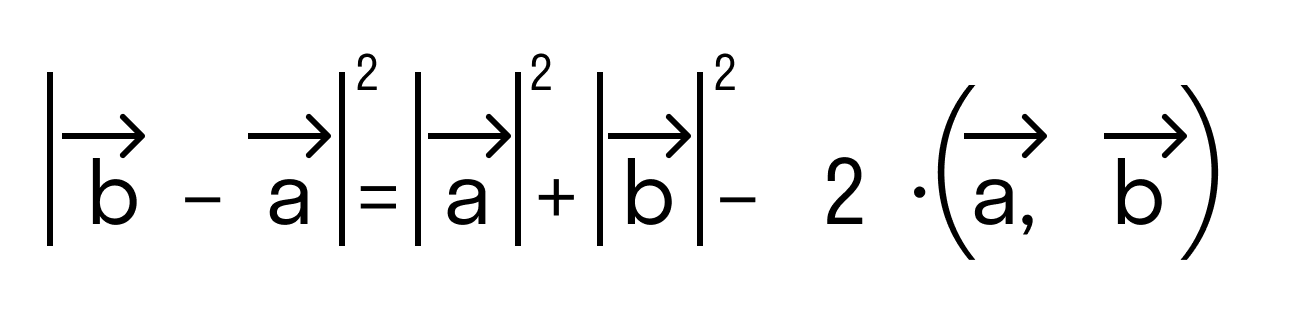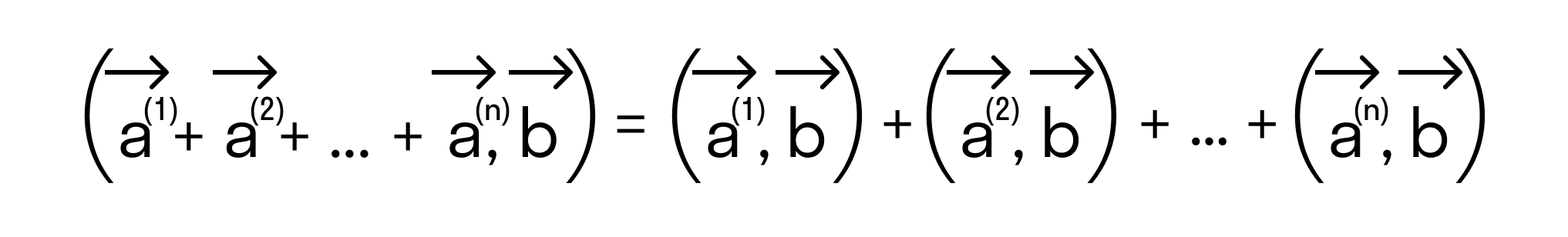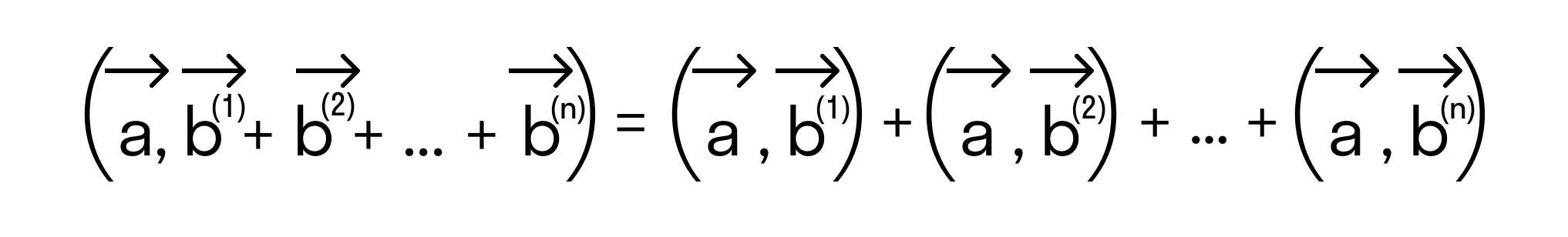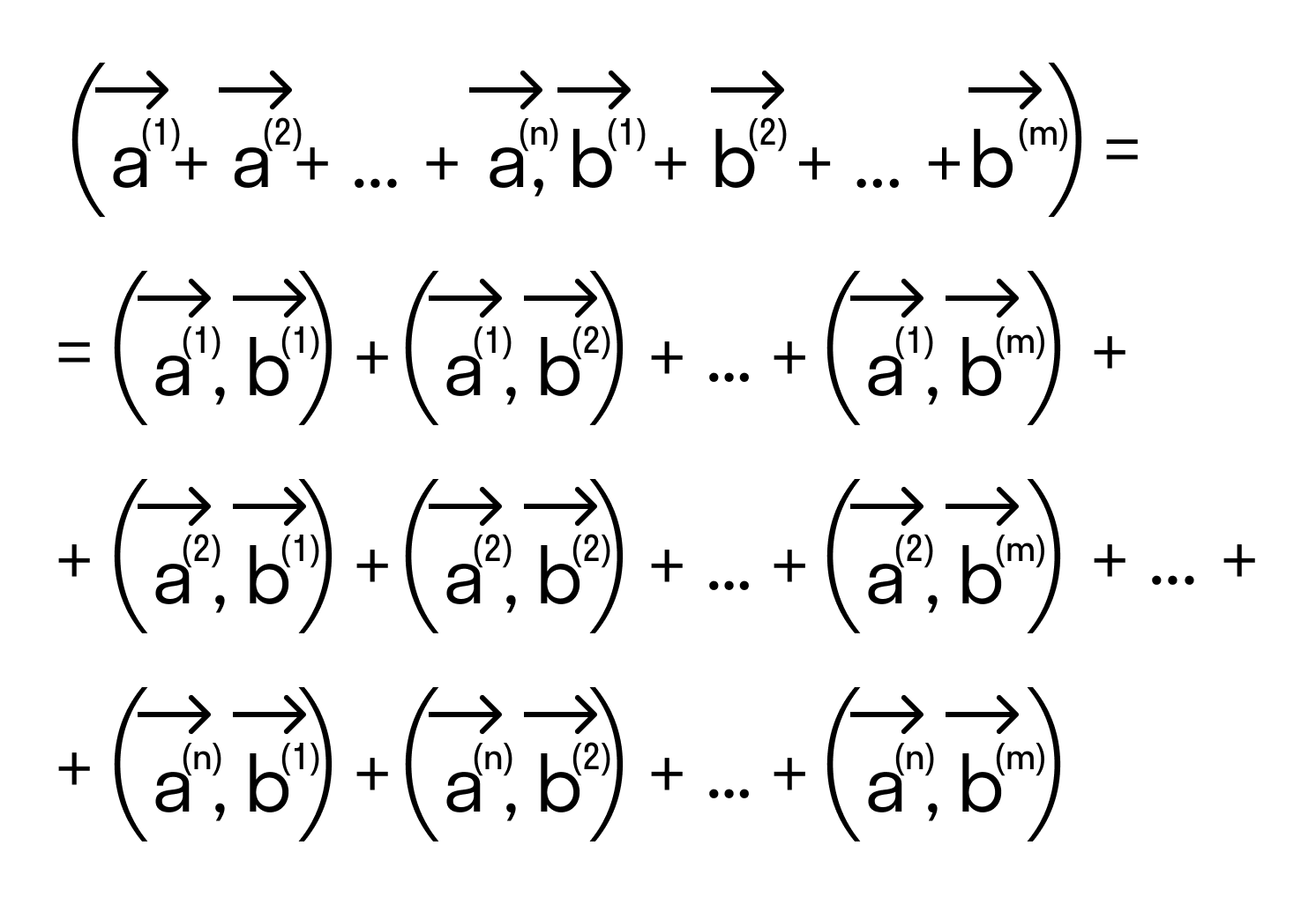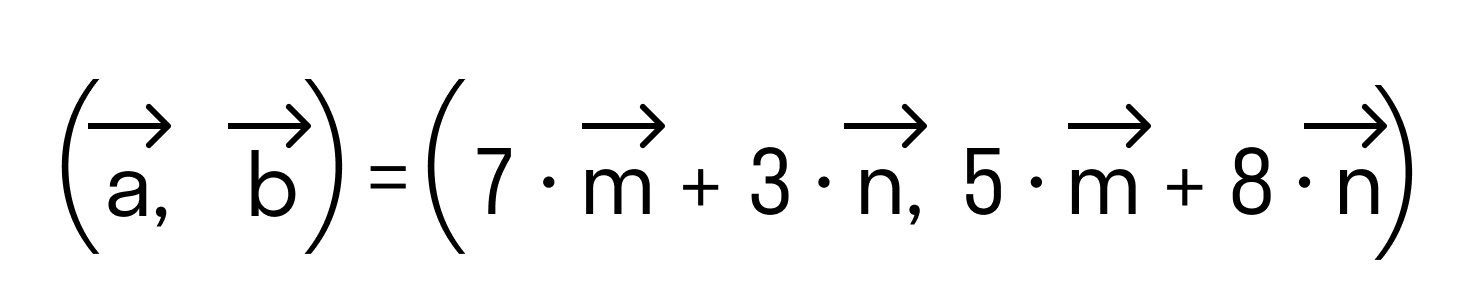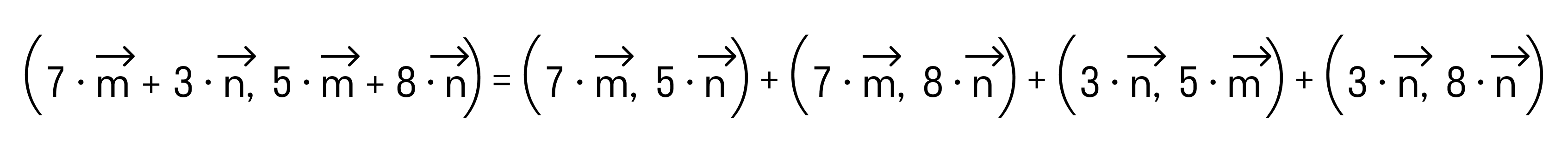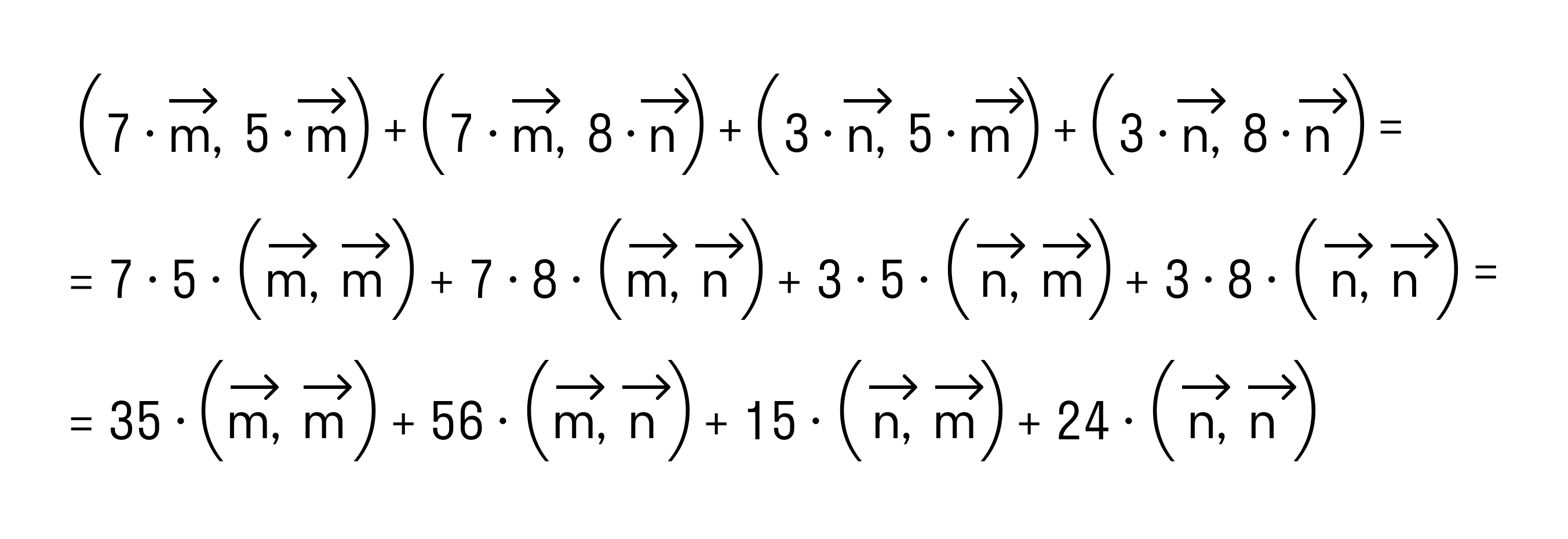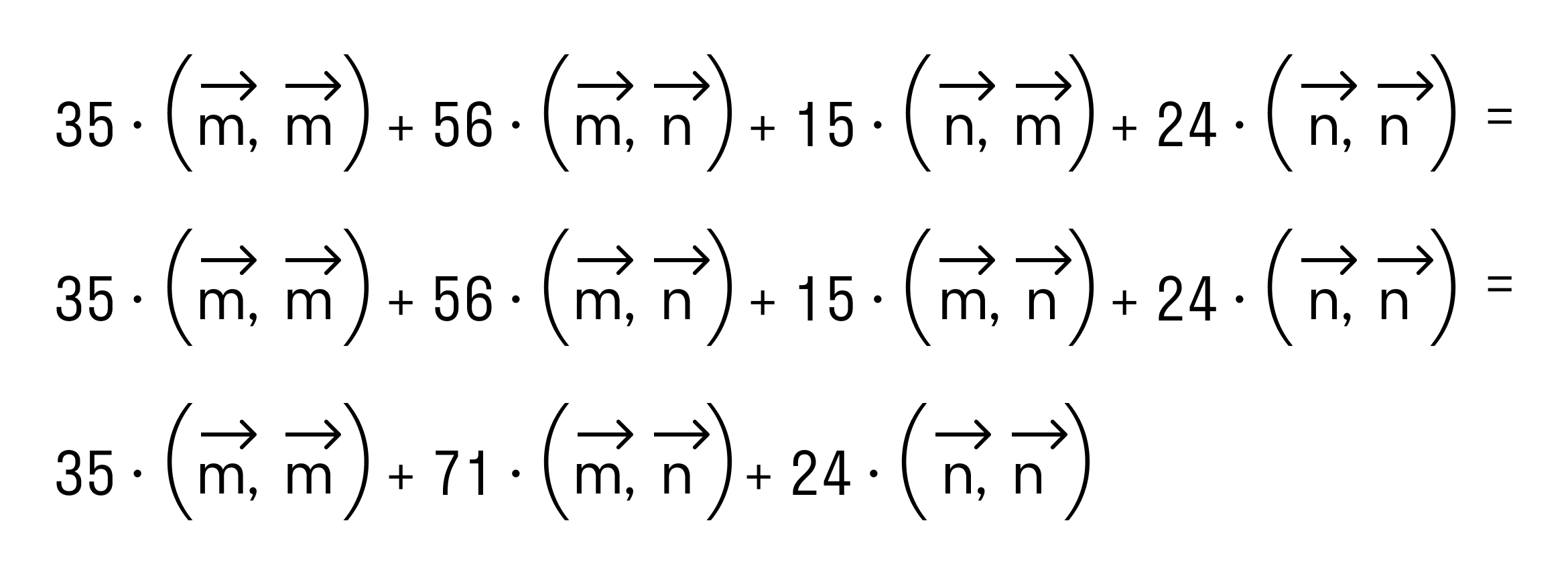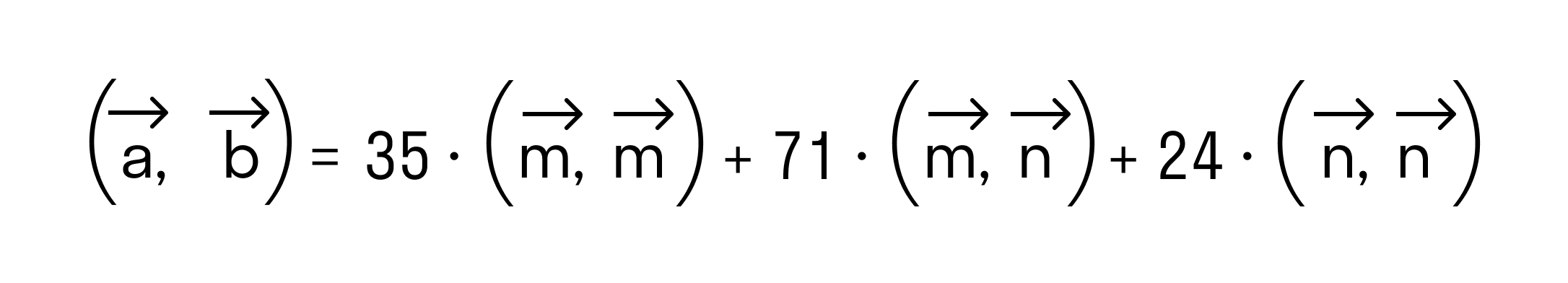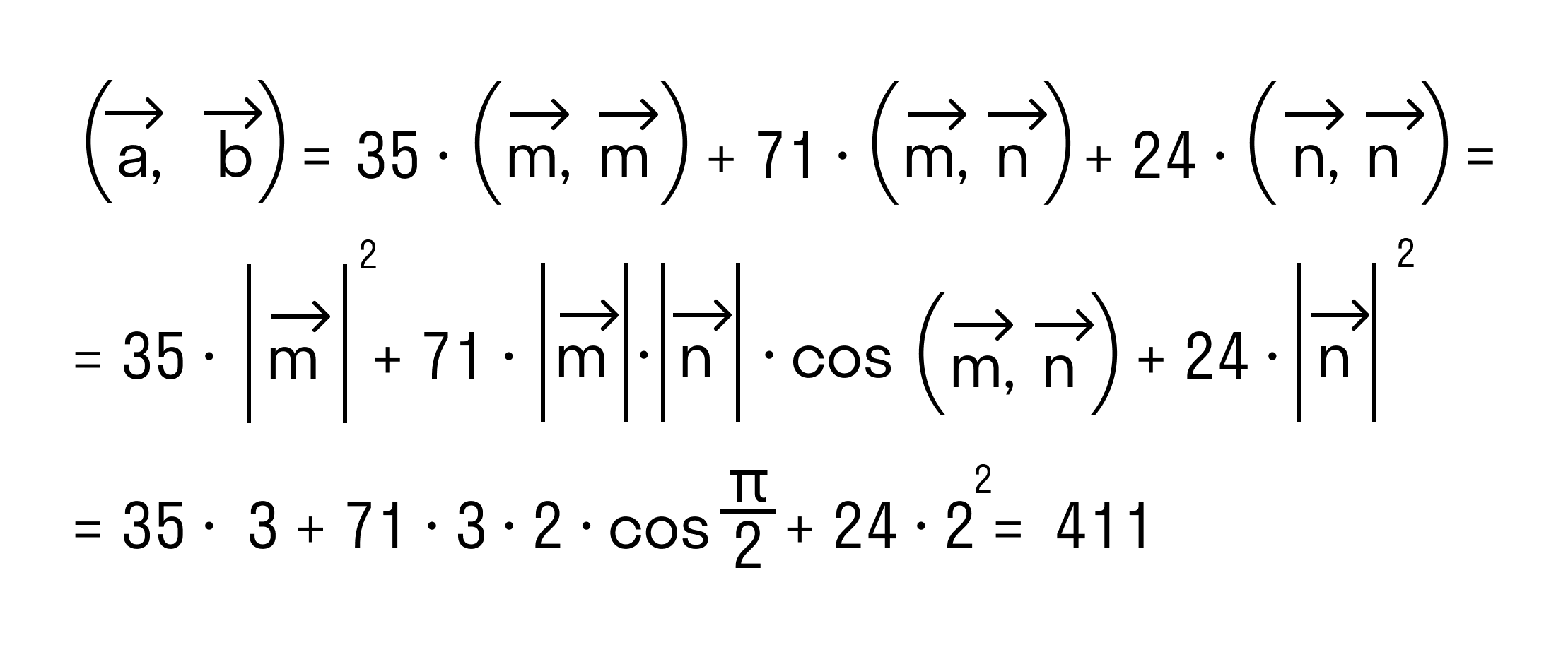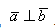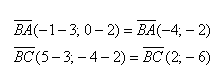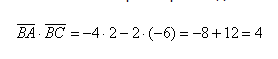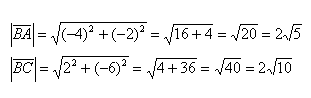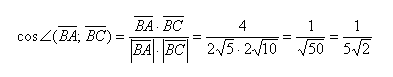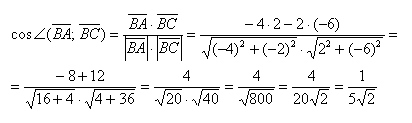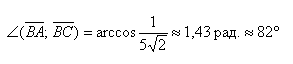какое выражение обозначает скалярное произведение векторов

Скалярное произведение векторов: свойства, примеры вычисления, физический смысл

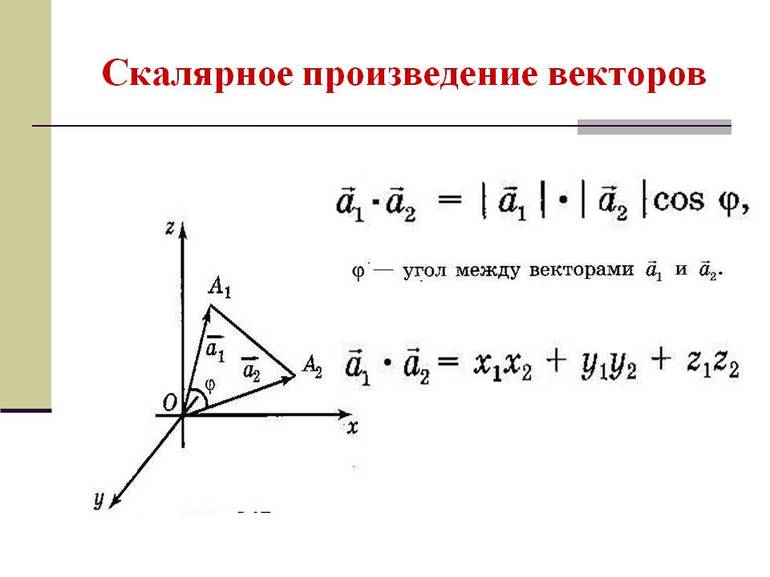
Скалярное произведение векторов называют число, равное произведению дин этих векторов на косинус угла между ними.

При умножении вектора самого на себя, получим квадрат его дины:

Скалярное умножение вектора самого на себя называют скалярным квадратом.

Вычисляется по формуле:

Сформулируем определение произведения для двух векторов:

Скалярное произведение двух векторов a → на b → называют произведение длины вектора a → на проекцию b → на направление a → или произведение длины b → на проекцию a → соответственно.

Скалярное произведение в координатах

Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.

для трехмерного пространства применимо выражение:

Фактически это является третьим определением скалярного произведения.

Следует отложить векторы

– соответственно для векторов трехмерного пространства.

Скалярное произведение и его свойства

Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел.

Дистрибутивность справедлива для любых чисел:

Скалярное произведение с примерами и решениями

Любая задача такого плана решается с применением свойств и формул, касающихся скалярного произведения:

Рассмотрим некоторые примеры решения.

Длина a → равна 3, длина b → равна 7. Найти скалярное произведение, если угол имеет 60 градусов.

По условию имеем все данные, поэтому вычисляем по формуле:

В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи:

Для начала вычисляются координаты векторов, так как по условию даны координаты точек:

Подставив в формулу с использованием координат, получим:

Выносим коэффициент за знак произведения и получим:

По свойству коммутативности преобразуем:

Теперь применим формулу для скалярного произведения с заданным по условию углом:

Если имеется числовая проекция.

Подставив в формулу, получим выражение:

Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.

Из формулы видно, что необходимо найти сумму произведений координат:

Физический смысл скалярного произведения

Механика рассматривает приложение скалярного произведения.

При работе А с постоянной силой F → перемещаемое тело из точки M в N можно найти произведение длин векторов F → и M N → с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения:

Источник

Скалярное произведение векторов

Основные определения

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

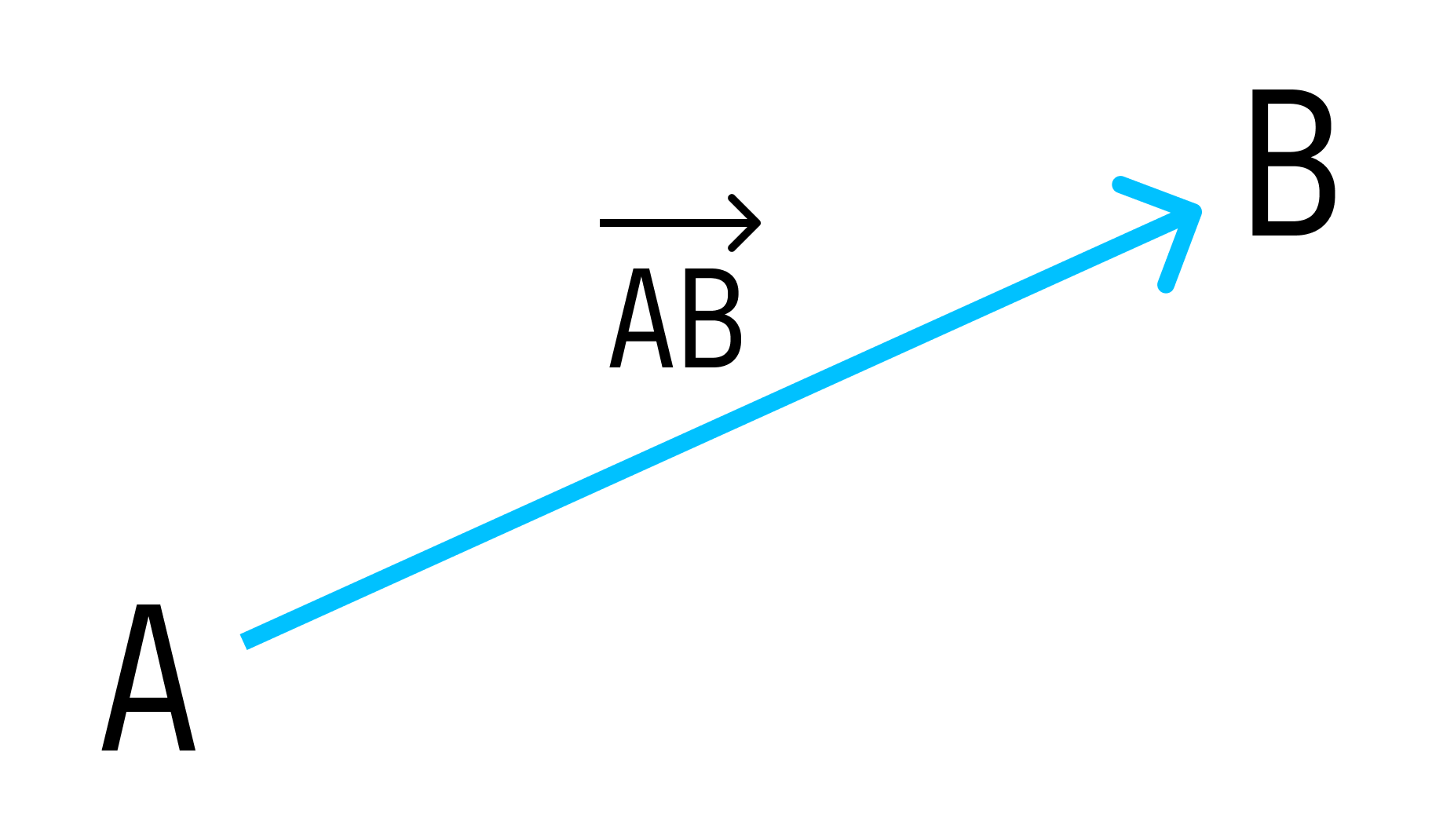
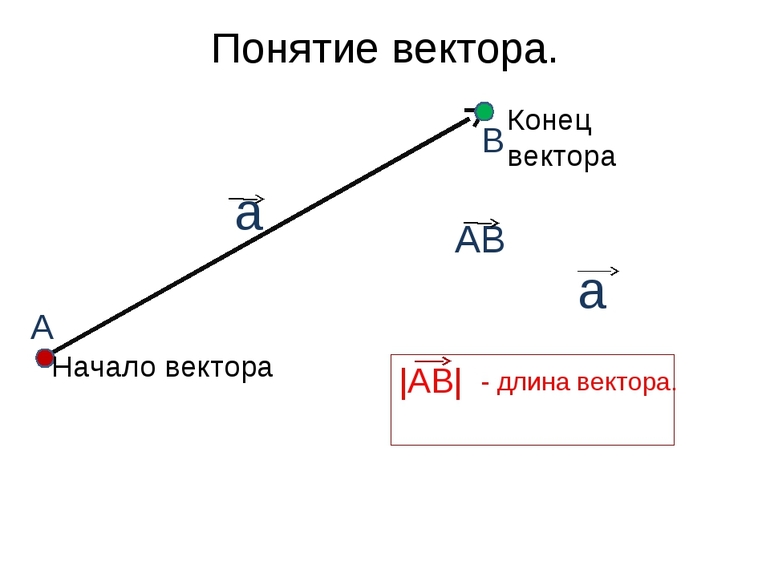
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.

Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.

Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.

Угол между векторами

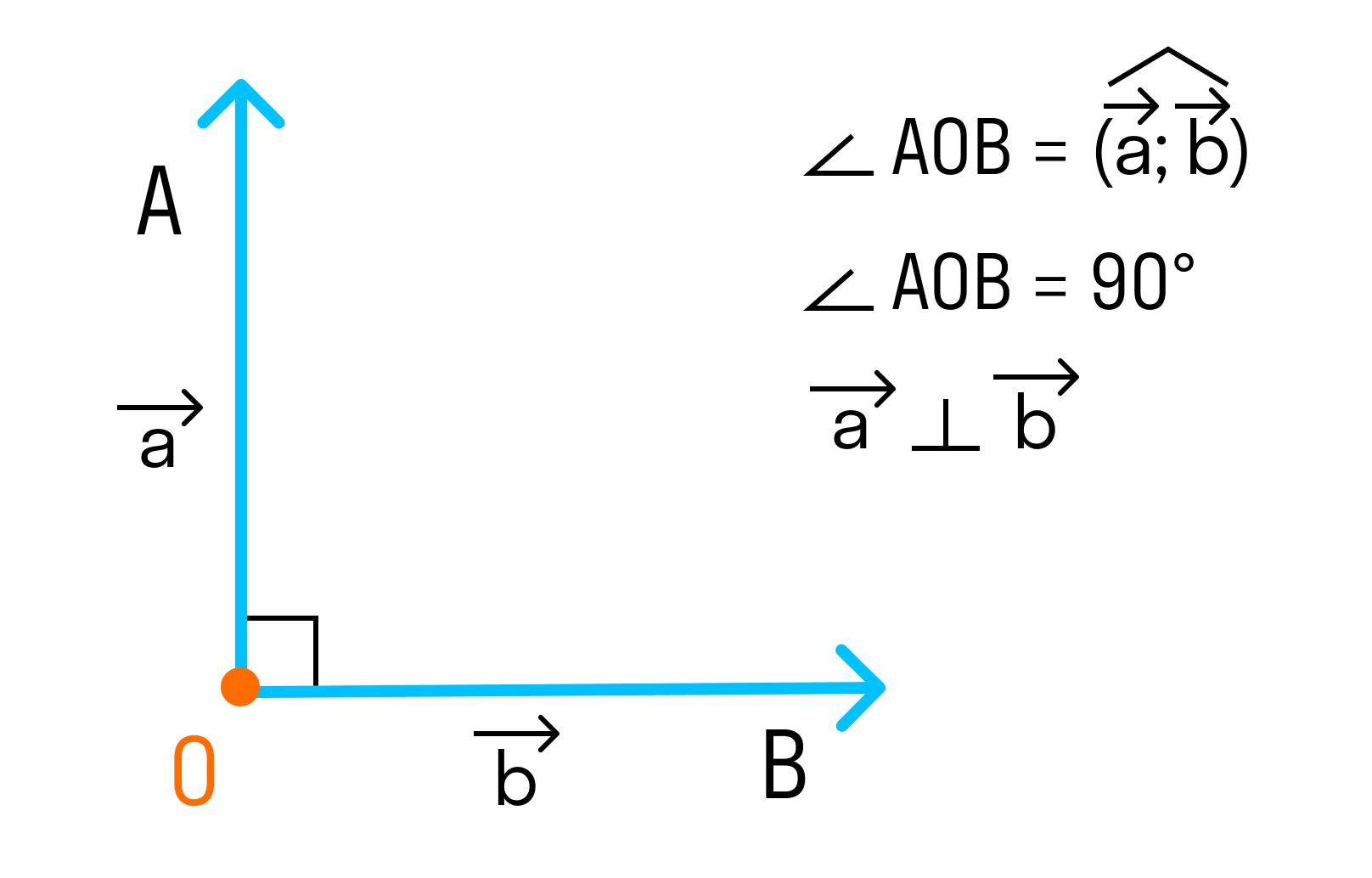
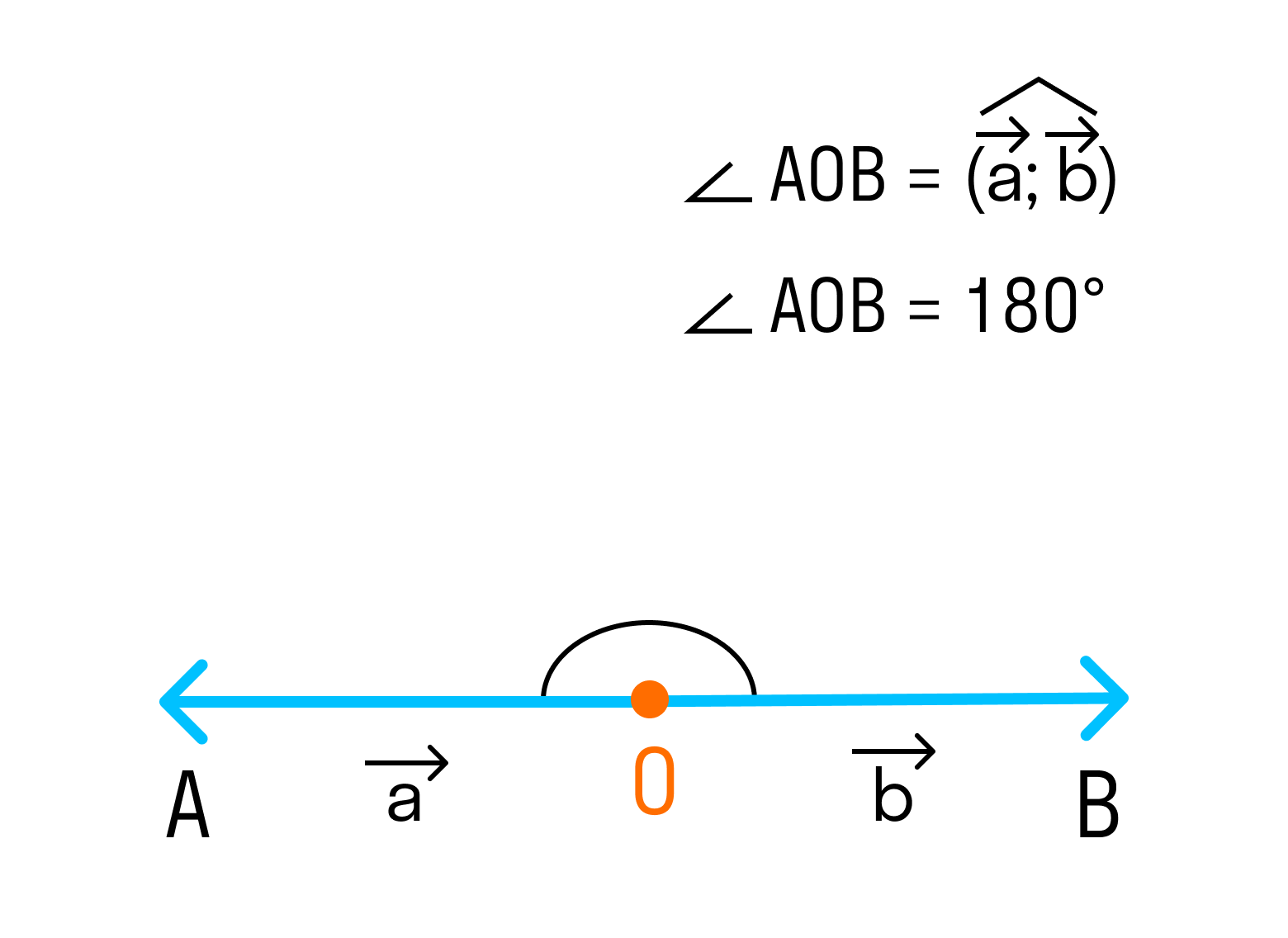
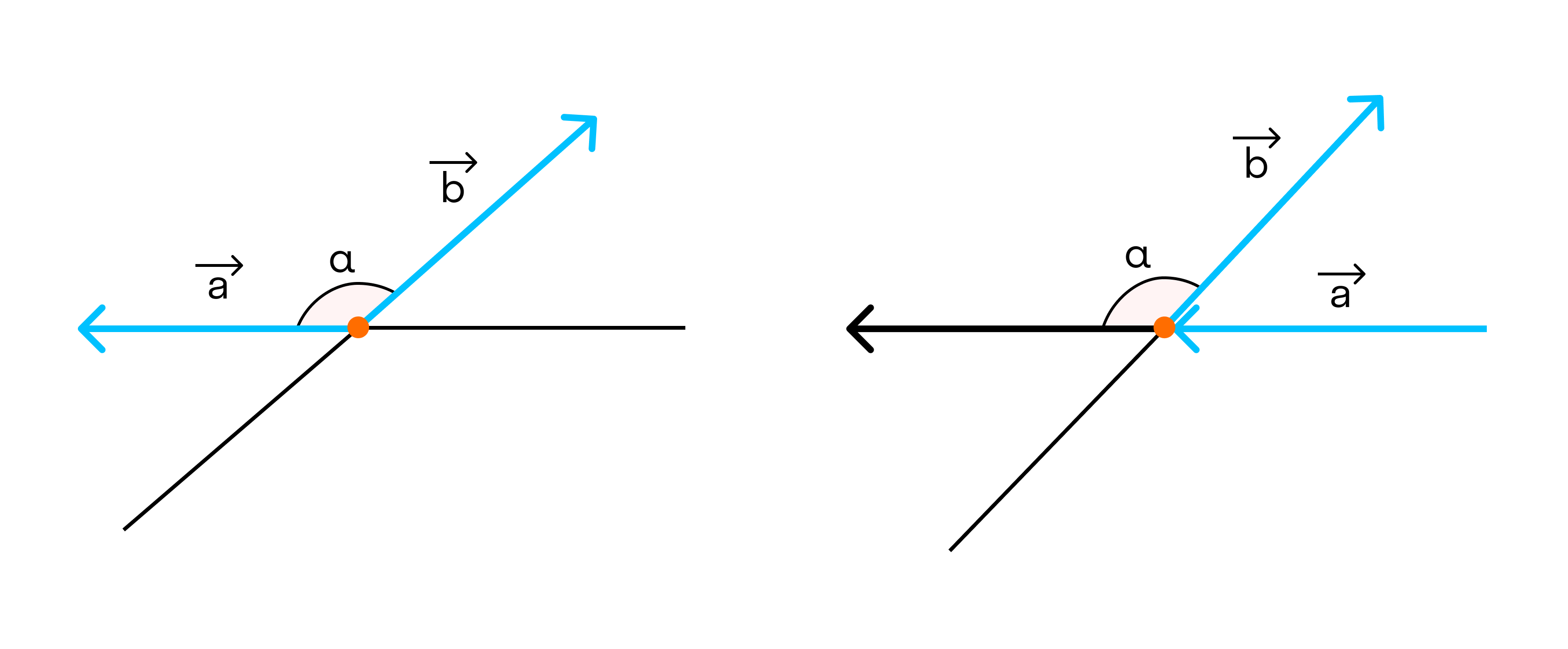
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=

2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.

3. Если векторы направлены в разные стороны, тогда угол между ними 180°.

Также векторы могут образовывать тупой угол. Это выглядит так:

Скалярное произведение векторов

Определение скалярного произведения можно сформулировать двумя способами:

Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.

Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:

Что важно запомнить про геометрическую интерпретацию скалярного произведения:

Скалярное произведение в координатах

Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.

То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by

А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz

Докажем это определение:

для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.

Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)

то последнее равенство можно переписать так:

а по первому определению скалярного произведения имеем

Записывайтесь на наши занятия по математике для учеников с 1 по 11 классы! Попробуйте пробный урок!

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В плоской задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by

Формула скалярного произведения векторов для пространственных задач

В пространственной задаче скалярное произведение векторов a = и b = можно найти по формуле:

a * b = ax * bx + ay * by + az * bz

Формула скалярного произведения n-мерных векторов

Свойства скалярного произведения

Свойства скалярного произведения векторов:

a ≠ 0, b ≠ 0, a * b = 0 a ┴ b

Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.

Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)

По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.

Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.

Аналогично доказываются остальные свойства скалярного произведения.

Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,

Примеры вычислений скалярного произведения

Пример 1.

Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.

У нас есть все данные, чтобы вычислить скалярное произведение по определению:

(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.

Ответ: (→a,→b) = 21/2 = 10,5.

Пример 2.

Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.

Используем формулу →a * →b = →|a| * →|b| * cosα.

→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3

Пример 3.

Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.

По свойству дистрибутивности скалярного произведения имеем

Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:

В силу свойства коммутативности последнее выражение примет вид

Итак, после применения свойств скалярного произведения имеем

Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:

Пример 4.

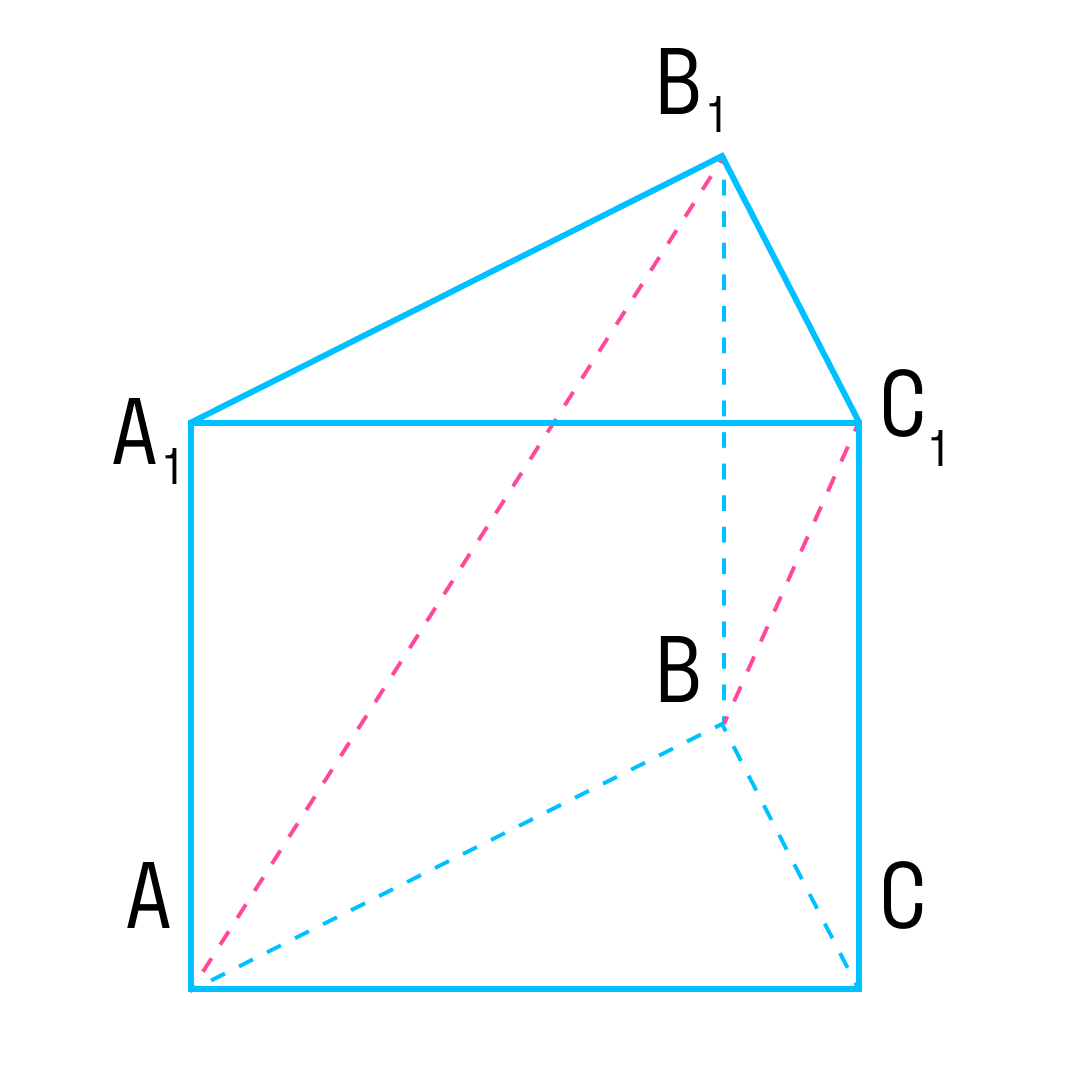
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.

Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.

Пример 5.

б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).

а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно

Обратите внимание на два существенных момента:

Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.

Пример 6.

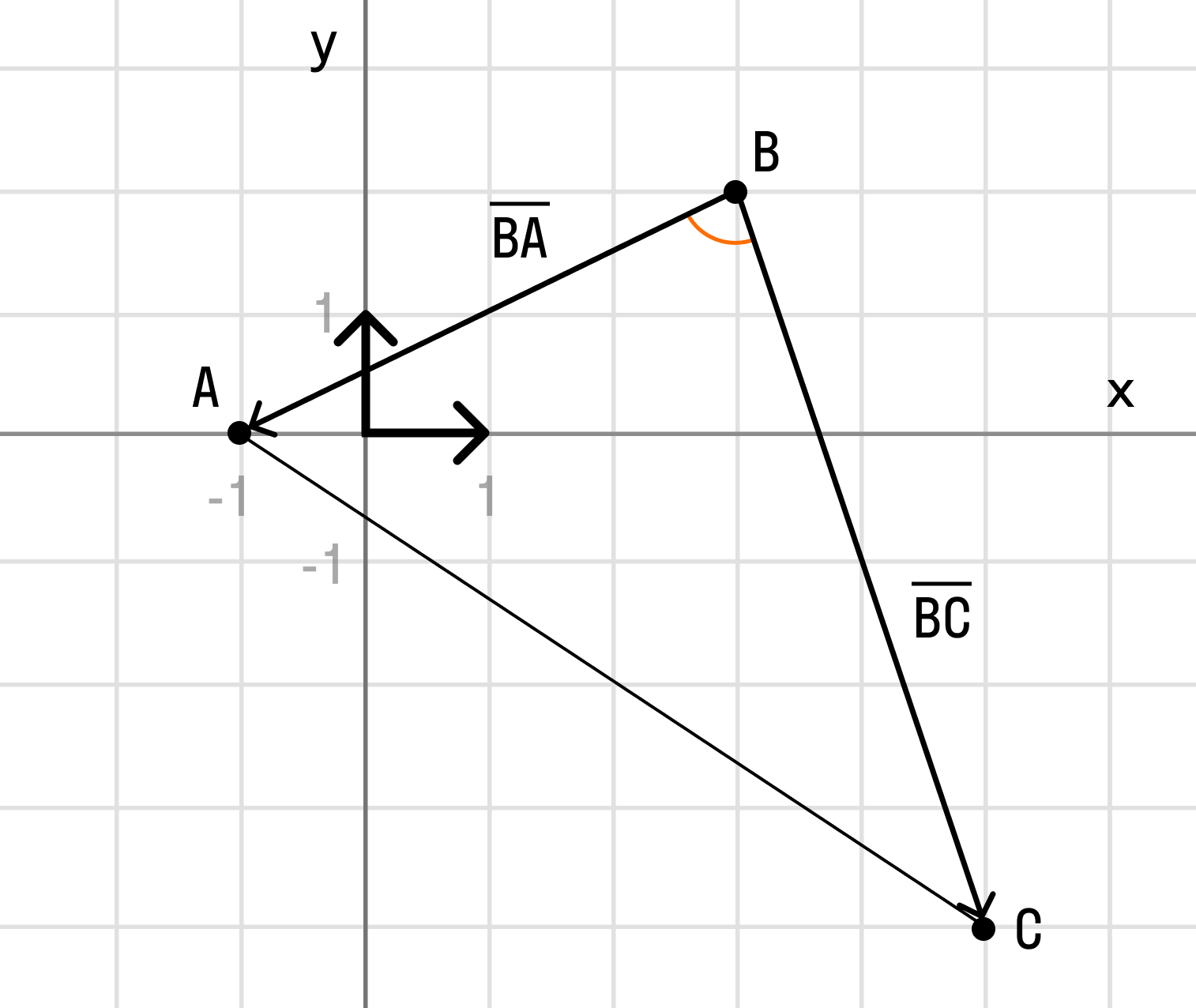
По условию чертеж выполнять не требуется, но для удобства можно сделать:

Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.

Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).

Вычислим скалярное произведение:

Вычислим длины векторов:

Найдем косинус угла:

Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:

Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.

Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.

Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°

Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.

А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.

Источник

Скалярное произведение векторов и его свойства

Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из двух векторов нулевой, то угол между ними не определён, а скалярное произведение считается равным нулю. Скалярное произведение векторов и обозначается

Скалярное произведение вектора самого на себя называется скалярным квадратам.

Решение. По определению находим

Геометрический смысл скалярного произведения векторов

Рассмотрим ортогональную проекцию ненулевого вектора на ось, задаваемую вектором (рис. 1.37). Согласно пункту 1 замечаний 1.4, алгебраическое значение длины проекции равно произведению длины вектора на косинус угла между векторами и :

Алгебраические свойства скалярного произведения

Для любых векторов и любого действительного числа :

Первое свойство определяет симметричность скалярного произведения, второе и третье — аддитивность и однородность по первому множителю, четвертое свойство — неотрицательность скалярного квадрата. Эти свойства аналогичны свойствам произведения чисел: первое свойство соответствует закону коммутативности умножения чисел, второе — закону дистрибутивности умножения по отношению к сложению, третье — закону ассоциативности умножения. Поэтому рассматриваемая операция и называется произведением векторов. Поскольку ее результатом является число (скаляр), то такое произведение векторов называется скалярным.

1. Свойства аддитивности и однородности скалярного произведения означают линейность скалярного произведения по первому множителю :

3. Для любых векторов справедливо неравенство Коши — Буняковского

4. Из неравенства Коши — Буняковского следует неравенство треугольника (длина стороны треугольника меньше суммы длин двух других его сторон и больше модуля их разности):

Геометрические свойства скалярного произведения

С помощью скалярного произведения можно находить основные метрические величины: длины отрезков (или, что то же самое, длины векторов) и величины углов.

2. Величина угла между ненулевыми векторами находится по формуле:

Отсюда заключаем, что:

— ненулевые векторы и перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю: ;

— угол между ненулевыми векторами и острый тогда и только тогда, когда их скалярное произведение положительно;

— угол между ненулевыми векторами и тупой \frac<\pi><2>\right)» png;base64,iVBORw0KGgoAAAANSUhEUgAAAFIAAAAmBAMAAAClsdF/AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAAZvHEYFEYuAx8CFysX6e75gAAAHwSURBVDjLY2AgCbCY4JBgFBQUZGBwcoALOE/ArtDpHRAUMLAjDLLBYaJRsGpTjAMDoy5MhNUAu0r2AuGNC0EMjgNQkX0JuDywQ/ohWMsSKF8Zp1eD2MBmMjZBuNzPcSlkXM4GNpOhbgOYYlqISyX7E56XYIZfAJiSUsClksOA7SmYIdwIpvIKcKnkTWC4BmZAjY7bgNNHAlCa7Q2YshMgGN2Mb8HkYhTBMGz6GFeARBkfowi6mmNRygi2l+0RiD2NgaH4JljQ1cYBU+k9kF8gAWHCwNTcATHNxxRTaVwCTCX7AYZaBw9o4hM33YBbpbADowkDMyyZijeBTGVRAgN1NJUMYgUMEjC/iBmBVIpgVSkhwLuB4RDcSLDtjFhtlyjwEBBvgTkTn4/YHivnWECc6dqKLZRActzgkJ/87lUIoZBnXAwm10BNUkdW6BMDCS9GSFCD1Yu9xhLdnOaHlyOlEIY4kBuYFmBLyRNY1oEdz/kGkZKFL2BROW8Jg14AUkoG5w5OLB5m2LWQIQ5cFvA2EshxjAIMeuBCwQ+S1bif4SnbVjkg5WJG3CUDA9NK5JIBT2nDUAX2OttqAiUY0J+d4OwpASvBGExxqZzswAbySyzBkpazLS0JGJ5sJgRLb2dgkQz0w2YHggXCZGNjY7h1ACJhdRVcflHKAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> тогда и только тогда, когда их скалярное произведение отрицательно.

Свойства 1 и 2 следуют непосредственно из определения скалярного произведения. Третье и четвертое свойства вытекают из геометрического смысла скалярного произведения (см. (1.8)) и п.1 замечаний 1.4.

Пример 1.14. Доказать тождества

Решение. Используя коммутативность и линейность скалярного произведения, запишем равенства

Заменяя скалярные квадраты векторов квадратами их длин (см. геометрическое свойство 1), получаем

Если из первого равенства вычесть второе, то придем к тождеству (а). Если же сложить оба равенства, то получим тождество (б).

Доказанные равенства выражают следующие свойства параллелограмма, построенного на векторах и ( и — его диагонали):

а) скалярное произведение векторов равно одной четвертой от разности квадратов диагоналей параллелограмма, построенного на множителях;

б) сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Источник

Трактовка понятий

Под скалярным произведением (СП) в пространстве над полем вещественных чисел подразумевается функция (x, y) для соответствующих элементов, принадлежащих указанному координатному пространству. Из определения вытекает линейность СП по первичному аргументу.

Для косинуса и синуса справедливо смешанное сопряжение. СП принимает положительную определённость, если соблюдается условие, что x=0. Для вычислений показателя в алгебре используется следующая форма: а = [a1, a2, …, an] и b = [b1, b2, …, bn].

Пример: нужно найти в трёхмерном пространстве произведение двух скаляров [1, 3, −5] и [4, −2, −1]. Решение: необходимо перемножить градиенты (вектора). [1, 3, −5] х [4, −2, −1] = 1 х 4 + 3 х (-2) + (-5) х (-1) = 3.

Геометрическое определение отличается от физического и алгебраического. Чтобы вычислить СП, используя длину и угол между градиентами, которые введены независимым способом, используется следующее выражение: (а, b) = lal x lbl x cos (a, b). Базисом аксиоматики считается скалярное произведение. После его нахождения определяется длина основного вектора и угла.

В современных теоремах понятие СП находится в основе некоторых производных, включая евклидову норму. Термин «длина» используется по отношению к конечномерным векторам. Если имеет смысл криволинейный путь, тогда применяются векторы ненулевой длины. Чаще они находятся в бесконечномерном пространстве.

Угол между такими величинами отличен от нуля. Его значением является число, косинус которого — отношение их СП к произведению их длин. Если пространство псевдоевклидовое (конечномерное, для которого характерна невырожденная индефинитная метрика), понятие «угол» применяется относительно скаляров без изотропных прямых.

Сам угол является числом. Чтобы дать ему значение, вычисляется гиперболический косинус: отношение модуля СП к произведению длин векторов. При перпендикулярности либо ортогональности на плоскости СП равняется нулю. Это свойство скалярного произведения векторов характерно для любого промежутка с положительно определённым СП.

При соблюдении такого условия пространство называется вещественным либо комплексным. Конечномерный вещественный промежуток с положительным СП называется евклидовым, а комплексный — унитарным (эрмитовым).

Если скалярное произведение отрицательное либо не считается знакоопределённым, промежуток называется индефинитной метрикой. Примером такого промежутка является пространство Минковского. СП на таких участках не порождает нормы. Из бесконечномерных выделяются пространства:

Описание свойств

С помощью специальных математических онлайн сервисов или калькулятора легко находится значение СП через теорему косинусов: a = arccos (a, b)/√(а, а)(b, b). Знак зависит от косинуса угла. В норме значения векторов только положительные. СП больше нуля, если угол острый, и меньше, когда он тупой.

Главные свойства умножения скаляров:

Задача 1: вычислить СП векторов а = <1;2>и b = <4;8>. Решение: а х b = 1 х 4 + 2 х 8 = 20.

Задача 2: найти СП скаляров а и b, если из длины равны 3 и 6, а угол — 60 градусов. Решение: а х b = lal x lbl cos α = 3 х 6 х cos60 = 9. Для лучшего усвоения материала два вектора перемножается с помощью матрицы. Чтобы различать множители, первый оформляется в строку, а второй — в столбец. Если в условиях задачи указываются три величины, тогда последняя оформляется в скобки в форме квадратов. Их скалярное произведение вычисляется путём умножения матриц. Результат — единственное число.

Применение в физике

Впервые скалярное произведение ввёл У. Гамильтон в 1846 году. Одновременно учёные начали использовать в своих работах векторное произведение, сумму скаляров. Понятие получило широкое применение и в физике. На его основе сформулированы главные законы электродинамики и механики.

Скаляр является физической величиной. Чтобы его задать, используется одно число. Примеры скаляров в физике:

В каждом предложенном варианте величина задаётся с помощью одного числа, поэтому масса тела и температура относятся к скалярам. Но это понятие в физике не считается простым числом. Для него характерна размерность.

Если в условиях задачи известно, что масса тела равна 3, необходимо указывать единицу измерения (килограммы, граммы). В математике можно сложить числа 3 и 10, а в физике суммируются только скаляры с одинаковой размерностью: массы с массой, градусы с градусами.

Если рассматривать векторную физическую величину, она характеризуется следующим образом:

Понятие скаляр — модуль вектора либо абсолютная величина. Если предположить, что транспортное средство двигается со скоростью 60 км/ч, такая информация считается неполной. В физике важно знать направление движения. Кроме модуля скорости как абсолютной величины, потребуется знать направление в пространстве, поэтому скорость считается векторной величиной.

Если на земле лежит кирпич массой в 1 кг и на него действует сила в 100 Н (модуль), потребуется найти направление движения объекта. Невозможно выяснить параметр, если нет информации о направлении действия силы. Если она идёт вверх, тогда и кирпич будет двигаться в аналогичном направлении.

Если сила идёт вдоль горизонта, тогда объект поедет горизонтально. При вертикальном воздействии силы вниз кирпич останется на прежнем месте. Он будет вжиматься в землю. Подобные явления указывают на то, что сила является вектором, поэтому для неё характерна размерность, модуль.

Для обозначения вектора в физике используются латинские буквы и стрелка:

Стрелка является направленным отрезком. Её начальная точка — начало вектора, а конечная или остриё — конец вектора. В математике величина с начальной точкой А и концом В обозначается →АВ. Если начало и конец направленного отрезка совпадают, тогда получается нулевой вектор. Он обозначается →0.

Такой отрезок считается точкой. У него нет конкретного направления, а длина равняется нулю. К безразмерным скалярам относятся коэффициенты трения и полезного действия, показатель преломления света.

Источник