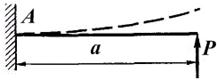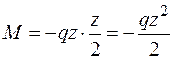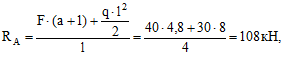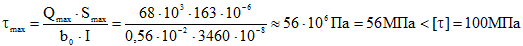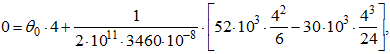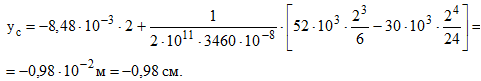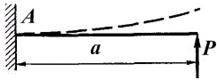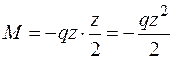какое сечение балки является опасным

Опасное сечение — это поперечное сечение, в котором действуют наибольшие внутренние усилия

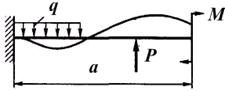
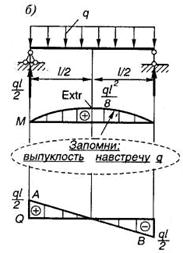
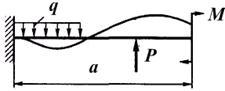
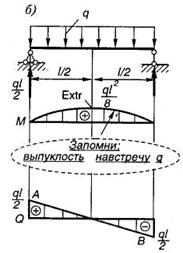
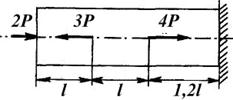
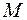
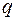
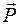
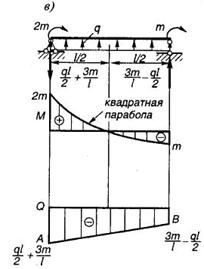
А где будет располагаться опасное сечение в более сложном случае нагружения (рис. 1.11, б)? Сразу дать правильный ответ до­статочно трудно, так как сосредоточенный изгибающий момент и распределенная нагрузка изгибают балку вниз, а сосредото­ченная сила — вверх, при этом величины моментов от каждого вида нагрузки различны.

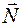
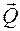
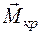
Поэтому для сложных случаев нагружения необходимо знать закон изменения по длине балки изгибающего момента или другого внутреннего усилия (например, продольной силы , поперечной силы или крутящего момента ). Этот закон можно изобразить с помощью специальных графиков, называемых эпюрами.

Эпюра — это график, изображающий закон изменения внутрен­него усилия по длине стержня.

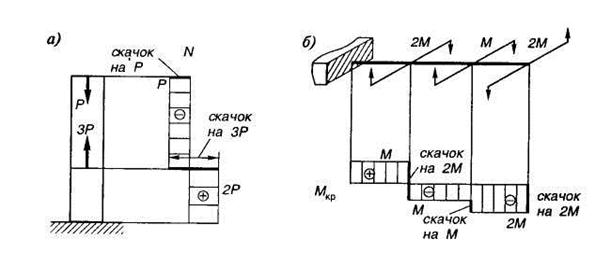
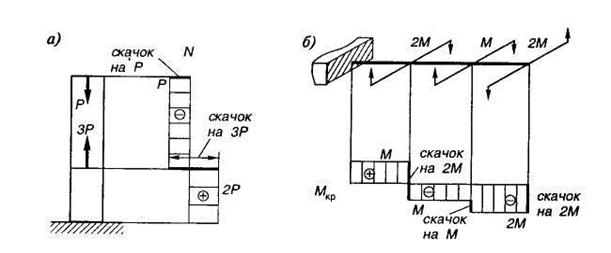
В случаях растяжения — сжатия (рис. 1.12, а) или кручения (рис. 1.12, б) ординаты эпюр продольных сил или крутящих моментов также показывают их величины в соответствующих поперечных сечениях.

Любое внутреннее усилие определяется по внешним нагрузкам при помощи метода сечений. Каждая эпюра на разных участках имеет различные знаки.

Правила знаков внутренних силовых факторов (ВСФ).

Рассмот­рим правила знаков для внутренних усилий, применяемые в маши­ностроении:

1. Продольная сила 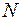считается положительной, если она вызывает растяжение отсеченной части и отрицательной, если вызывает ее сжатие.

2. Поперечная сила 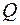считается положительной, если она вращает отсеченную часть по ходу часовой стрелки и отрицательной, если вращение происходит против хода часовой стрелки.

3. Изгибающий момент положителен, если сжаты верхние волокна отсеченной части, и отрицателен, если сжаты нижние волокна. Эпюра изгибающих моментов строится на сжатых волокнах.

4. Правило знаков для крутящего момента удобно принимать произвольным.

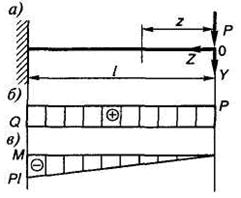
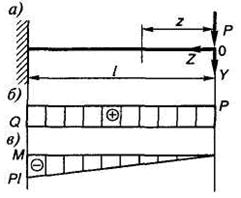
Запишем выражение изгибающих моментов для текущегосечения z, например, в консольной балке, находящейся под действи­емсосредоточенной силы (рис. 1.12):

— уравнение прямой.

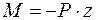
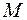
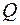
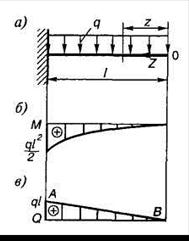
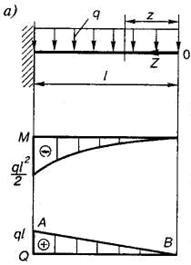
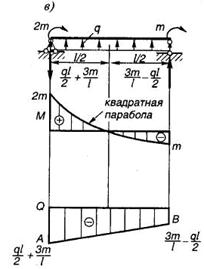
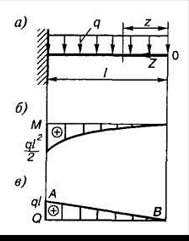
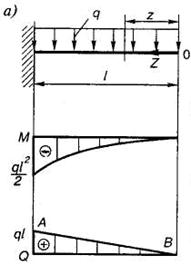
Из этого следует, что на прямолинейном ненагруженном вне­шней пролетной нагрузкой участке стержня эпюра моментов пря­молинейна, а эпюра поперечных сил постоянна (рис. 1.13, а, б, в).

Запишем выражение изгибающих моментов для текущего сечения z в случае изгиба консольной балки, находящейся под действием равномерно распределенной нагрузки (рис. 1.14, а):

— это уравнение квадратной параболы.

В соответствии с дифференциальной зависимостью Журавского:

— уравнение прямой.

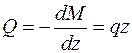
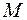
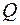
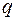
Таким образом, на участке с распределенной нагрузкой эпюры изгибающих моментов очерчены по квадратичной параболе с выпуклостью навстречу действию распределенной нагрузки, а эпюра поперечных сил имеет вид трапеции или треугольника и ограни­чена прямой наклонной линией АВ, при этом направление наклона (при обходе слева направо) совпадает с направлением (рис. 1.13 и 1.14).

Примеры построения эпюр (рис. 1.15).

3. напряжения и деформации

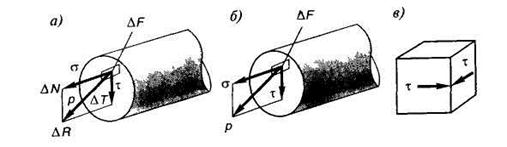
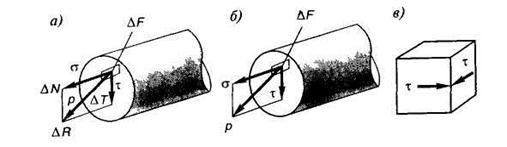
Интенсивность, равная величине внутренних сил, приходящихся на единицу площади называется напряжением в точке (рис. 1.16) и является ключевым понятием в сопромате.

Существует 2 вида напряжений:

,

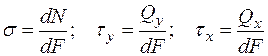
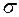
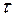
причем (сигма) — нормальное напряжение,действует по нормали (перпендикуляру) к площадке;

(тау) — касательные напряжения, они скользят по площадке, касаются ее(рис. 1.16, в).

Напряжения измеряются в Н/м 2 (Па) и МПа. Иногда используют полное напряжение (рис. 1.16, а, б).

.

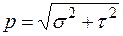
Понятие о деформациях. Реальные тела под воздействием внеш­них сил могут изменять свою форму и размеры — деформироваться. Определение величины этих изме­нений называется расчетом на

жест­кость.

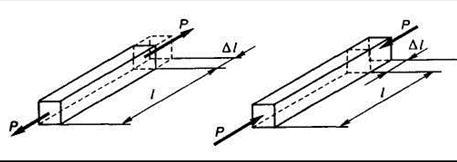
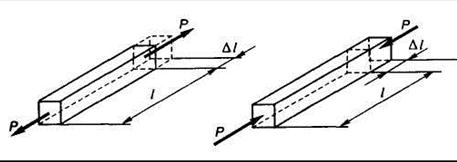
Все возможные изменения формы мо­жно оценить, используя всего лишь два вида деформаций — линейные(рис. 1.17) и угловые(рис. 1.18).

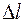
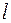
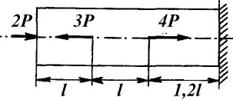
При нагружении растягивающими си­лами стержень удлиняется. Изменение первоначальной длины стержня называется абсолютным удлинени­ем.

Центральное растяжение (сжатие) возникает в случае, ког­да стержень нагружен силами, совпадающими по направлению с его осью (рис. 1.120). В этом случае из шести внутренних силовых факторов пять равны нулю и только продольная сила .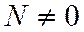

На растяжение, сжатие ра­ботают многие элементы кон­струкций: стержни ферм, ко­лонны, штоки паровых машин и поршневых насосов, стяжные винты, канаты лебедок и другие детали.

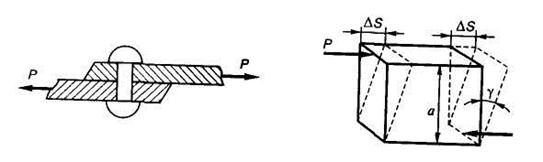
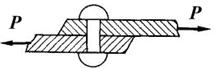
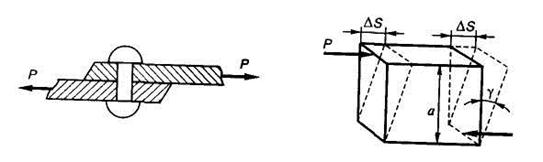
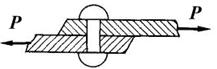
Сдвиг или срез возникает, когда внешние силы смещают два параллельных сечения одно относительно другого, при неизменном расстоянии между ними. На сдвиг или срез работают, например, заклепки или болты, скрепляющие элементы, которые внешние силы пытаются сдвинуть (рис. 1.21).

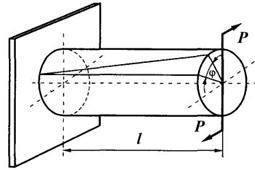
Кручение возникает при действии на стержень внешних сил, образующих моменты от­носительно продольной оси стержня. При этом из шести внутренних сил только 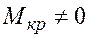. На круче­ние работают валы, шпин­дели токарных и сверлиль­ных станков, роторы дви­гателей и другие детали (рис. 1.22).

Изгиб — это такой вид нагру­жения, когда внешние силы вызыва­ют моменты относительно оси сим­метрии (или главной оси), расположенный в плоскости поперечного се­чения. Этот момент называется изгибающим. Самый простой случай — это плоский изгиб, когда все внешние силы лежат в одной плоскости, совпадающей во всех рассматриваемых нами случаях с плоскостью симметрии (или глав­ной плоскостью) балки.

Источник

iSopromat.ru

Пример решения задачи полного расчета на прочность и жесткость стальной двутавровой балки для заданной системы изгибающих нагрузок.

Задача

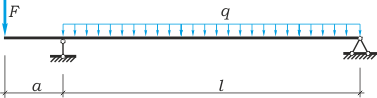
Произвести полный расчет на прочность и проверить жесткость статически определимой двутавровой двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [ σ ]=160 МПа и [ τ ]=100 МПа, допустимый прогиб балки [f]= l/400

Решение

Определение опорных реакций

Подробно, пример определения опорных реакций для балки рассмотрен здесь

А также в нашем коротком видеоуроке:

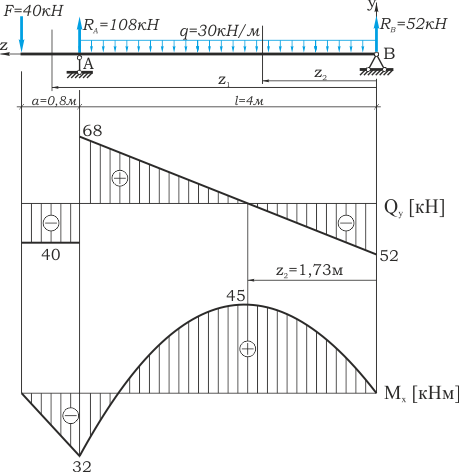
Построение эпюр Q и М

Видео про расчет значений Q и M для построения эпюр:

По этим данным построены эпюры Q и М.

Короткое видео о том, как надо строить эпюры:

Подбор сечения двутавровой балки

Так как М_mах = 45 кНм, то

Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.

Проверка сечения балки по касательным напряжениям

Так как Q_max = 68 кН, то

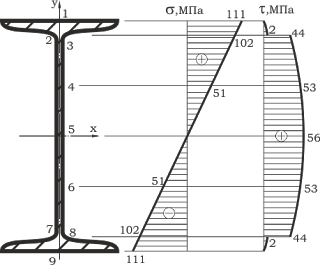
Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:

В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:

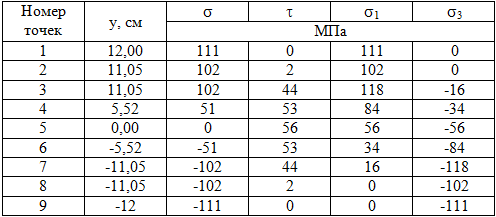
Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1

Проверка прочности балки по главным напряжениям

Прогиб в пролете при z=l/2=4/2=2 м.

Аналогично определяется прогиб на конце консоли при z = l + a =4+0,8 = 4,8 м.

Проверка жесткости балки

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Расчет балки и определение прогибов при косом изгибе

Задача. Для балки построить эпюры изгибающих моментов, проверить прочность, определить положение нулевой линии в сечении, построить эпюру нормальных напряжений, определить величину и направление прогиба на границе участков балки (в точке С).

Дано: сечение из двух двутавров №16, материал балки сталь Ст3, допускаемое напряжение [σ]=160 МПа, модуль упругости Е=2·10 5 МПа.

а) Покажем балку с нагрузкой по оси у (рис.а) и построим эпюру изгибающих моментов М_х.

Сначала определим опорные реакции R_А и R_В.

Строим Эп. М_х методом характерных точек. Характерные точки – начало и конец участков, середина равномерно распределенной нагрузки – т. К.

б) Покажем балку с нагрузкой в плоскости х (рис. в), определяем опорные реакции и построим Эп. М_у.

Строим эпюру М_у методом характерных точек.

Строим эп. М_у (рис. г)

2.Проверим прочность балки по формуле:

Значения М_х и М_у возьмем с эпюр М_х и М_у по опасному сечению, а W_х и W_у для заданного сечения следует определить по формулам:

Выполним чертеж сечения в масштабе

Определим главные центральные моменты инерции всего сечения по формулам перехода:

Определим осевые моменты сопротивления

Проверка прочности. Рассмотрим возможные опасные сечения.

Проверим сечение С, где М_х=14,4 кНм, М_у=3,6 кНм.

Проверим сечение К, где М_х=16,2 кНм, М_у=3,3 кНм.

Из сравнения заключаем, что опасным сечением балки является сечение К.

Проверяем прочность:

Прочность обеспечена.

Сначала определим положение нулевой линии в сечении К.

Уравнение нулевой линии:

Определим координаты двух точек нулевой линии

Строим сечение в масштабе и проводим нулевую линию.

Эпюра нормальных напряжений σ. Для определения напряжений по формуле

определим координаты необходимых точек в сечении (1,2,3,4):

Строить эп. σ будем для опасного сечения в т.К.

Определим напряжения в точках:

Строим эпюры напряжений в точках по периметру сечения и общую эпюру напряжений σ.

Для этого параллельно нулевой линии проводим прямые от наиболее удаленных точек сечения (точки 2 и 4), перпендикулярно им наносим базисную линию (нулевую линию для общей эпюры напряжений σ), и строим на ней общую эпюру σ.

4.Определим прогиб на границе смежных участков, т.е. в точке С. Прикладываем в т. С единичную силу (рис. д), определяем опорные реакции и строим эпюру единичных моментов (рис.е).

Определение опорных реакций.

Определим изгибающие моменты в точках.

Строим эпюру единичных моментов.

Определение перемещений.

Перемещение определим по формуле Симпсона

Построим схему прогибов в масштабе и измерим по чертежу Δ=4,8см.

Вычислим прогиб аналитически:

Результаты приблизительно равны.

Проверка: линия прогиба должна быть перпендикулярна нулевой линии. Проверка выполняется.

Источник

Опасное сечение — это поперечное сечение, в котором действуют наибольшие внутренние усилия

А где будет располагаться опасное сечение в более сложном случае нагружения (рис. 1.11, б)? Сразу дать правильный ответ до­статочно трудно, так как сосредоточенный изгибающий момент и распределенная нагрузка изгибают балку вниз, а сосредото­ченная сила — вверх, при этом величины моментов от каждого вида нагрузки различны.

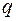
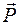
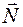
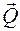
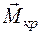
Поэтому для сложных случаев нагружения необходимо знать закон изменения по длине балки изгибающего момента или другого внутреннего усилия (например, продольной силы , поперечной силы или крутящего момента ). Этот закон можно изобразить с помощью специальных графиков, называемых эпюрами.

Эпюра — это график, изображающий закон изменения внутрен­него усилия по длине стержня.

В случаях растяжения — сжатия (рис. 1.12, а) или кручения (рис. 1.12, б) ординаты эпюр продольных сил или крутящих моментов также показывают их величины в соответствующих поперечных сечениях.

Любое внутреннее усилие определяется по внешним нагрузкам при помощи метода сечений. Каждая эпюра на разных участках имеет различные знаки.

Правила знаков внутренних силовых факторов (ВСФ).

Рассмот­рим правила знаков для внутренних усилий, применяемые в маши­ностроении:

1. Продольная сила 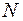считается положительной, если она вызывает растяжение отсеченной части и отрицательной, если вызывает ее сжатие.

2. Поперечная сила 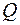считается положительной, если она вращает отсеченную часть по ходу часовой стрелки и отрицательной, если вращение происходит против хода часовой стрелки.

3. Изгибающий момент положителен, если сжаты верхние волокна отсеченной части, и отрицателен, если сжаты нижние волокна. Эпюра изгибающих моментов строится на сжатых волокнах.

4. Правило знаков для крутящего момента удобно принимать произвольным.

Запишем выражение изгибающих моментов для текущегосечения z, например, в консольной балке, находящейся под действи­емсосредоточенной силы (рис. 1.12):

— уравнение прямой.

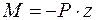
Из этого следует, что на прямолинейном ненагруженном вне­шней пролетной нагрузкой участке стержня эпюра моментов пря­молинейна, а эпюра поперечных сил постоянна (рис. 1.13, а, б, в).

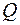
Запишем выражение изгибающих моментов для текущего сечения z в случае изгиба консольной балки, находящейся под действием равномерно распределенной нагрузки (рис. 1.14, а):

— это уравнение квадратной параболы.

В соответствии с дифференциальной зависимостью Журавского:

— уравнение прямой.

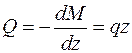
Таким образом, на участке с распределенной нагрузкой эпюры изгибающих моментов очерчены по квадратичной параболе с выпуклостью навстречу действию распределенной нагрузки, а эпюра поперечных сил имеет вид трапеции или треугольника и ограни­чена прямой наклонной линией АВ, при этом направление наклона (при обходе слева направо) совпадает с направлением (рис. 1.13 и 1.14).

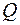
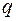
Примеры построения эпюр (рис. 1.15).

3. напряжения и деформации

Интенсивность, равная величине внутренних сил, приходящихся на единицу площади называется напряжением в точке (рис. 1.16) и является ключевым понятием в сопромате.

Существует 2 вида напряжений:

,

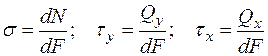
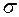
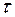
причем (сигма) — нормальное напряжение, действует по нормали (перпендикуляру) к площадке;

(тау) — касательные напряжения, они скользят по площадке, касаются ее(рис. 1.16, в).

Напряжения измеряются в Н/м 2 (Па) и МПа. Иногда используют полное напряжение (рис. 1.16, а, б).

.

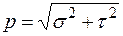
Понятие о деформациях. Реальные тела под воздействием внеш­них сил могут изменять свою форму и размеры — деформироваться. Определение величины этих изме­нений называется расчетом на

жест­кость.

Все возможные изменения формы мо­жно оценить, используя всего лишь два вида деформаций — линейные(рис. 1.17) и угловые(рис. 1.18).

При нагружении растягивающими си­лами стержень удлиняется. Изменение 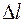первоначальной длины стержня называется абсолютным удлинени­ем.

Центральное растяжение (сжатие) возникает в случае, ког­да стержень нагружен силами, совпадающими по направлению с его осью (рис. 1.120). В этом случае из шести внутренних силовых факторов пять равны нулю и только продольная сила .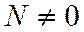

На растяжение, сжатие ра­ботают многие элементы кон­струкций: стержни ферм, ко­лонны, штоки паровых машин и поршневых насосов, стяжные винты, канаты лебедок и другие детали.

Сдвиг или срез возникает, когда внешние силы смещают два параллельных сечения одно относительно другого, при неизменном расстоянии между ними. На сдвиг или срез работают, например, заклепки или болты, скрепляющие элементы, которые внешние силы пытаются сдвинуть (рис. 1.21).

Кручение возникает при действии на стержень внешних сил, образующих моменты от­носительно продольной оси стержня. При этом из шести внутренних сил только 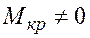. На круче­ние работают валы, шпин­дели токарных и сверлиль­ных станков, роторы дви­гателей и другие детали (рис. 1.22).

Изгиб — это такой вид нагру­жения, когда внешние силы вызыва­ют моменты относительно оси сим­метрии (или главной оси), расположенный в плоскости поперечного се­чения. Этот момент называется изгибающим. Самый простой случай — это плоский изгиб, когда все внешние силы лежат в одной плоскости, совпадающей во всех рассматриваемых нами случаях с плоскостью симметрии (или глав­ной плоскостью) балки.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник