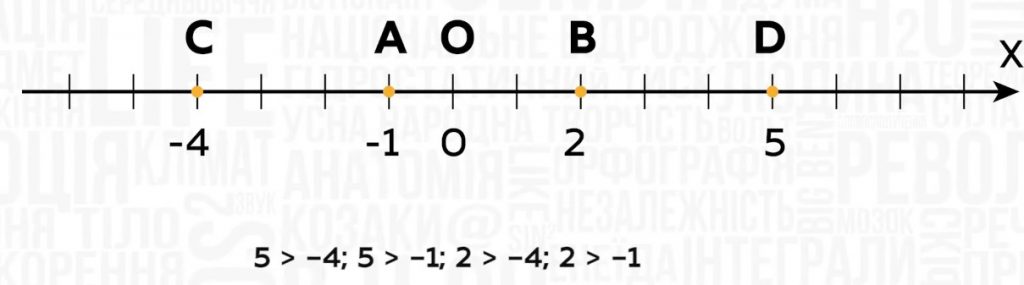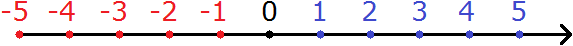какое отрицательное число больше а какое меньше
Сравнение положительных и отрицательных чисел
Из этого урока вы научитесь сравнивать рациональные числа.
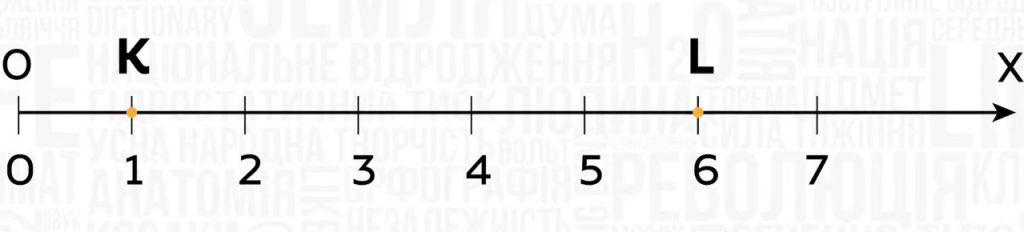
На координатном луче точка L с координатой 6 расположена правее точки К с координатой 1. Поэтому 6 > 1.
Следовательно, большим из двух чисел есть число, расположенное на координатной прямой правее.
Помни, что на координатной прямой любое отрицательное число расположено левее любого положительного числа. Поэтому любое отрицательное число всегда меньше любого положительного числа.
Например, пять больше минус четыре; пять больше минус один; два больше минус четыре; два больше минус один.
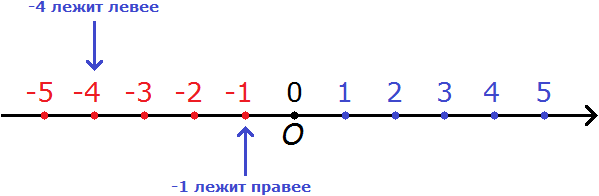
На рисунке точка А с координатой минус один лежит правее (ближе нуля) от точки С с координатой минус четыре, поэтому минус один больше минус четыре. Заметим, что модуль минус один меньше модуля минус четыре. Следовательно, из двух отрицательных чисел больше то, модуль которого меньше.
На координатной прямой число 0 расположено левее любого положительного числа и правее любого отрицательного числа.
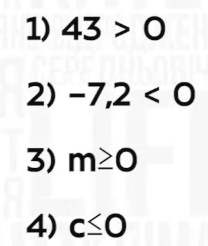
Следовательно, любое положительное число больше нуля. Записывают в виде неравенства: a > 0.
Любое отрицательное число меньше нуля. Записывают в виде неравенства: a ≥ 0. Читают: «а больше или равно нулю».
Если а – не положительное число (т.е. отрицательное или ноль), то пишут а ≤ 0. Читают: «а меньше или равно нулю»
Используя эти обозначения запишем свойство модуля числа а так:
модуль «а» равен «а», если «а больше или равен нулю»;
модуль «а» равен «-а», если «а меньше нуля».
Решаем задачи
Задание 1:
Какая из двух точек расположена справа от другой:
Решение:
Задание 2:
Запишите в виде неравенства утверждение:
Решение:
любое положительное число больше нуля, следовательно, 43 > 0;
поскольку «С» – не положительное число, то «С» ≤ 0.
Задание 3:
Решение:
По условию следует записать числа от наибольшего к наименьшему.
Наибольшим из чисел, расположенным на координатной прямой справа, является число 7,23. Затем 2; 0,2; 0.
Поскольку среди отрицательных чисел наибольшее число то, у которого модуль наименьший, поэтому сравним модули отрицательных чисел:
Ответ:
Вы научились сравнивать рациональные числа. Для закрепления этого навыка выполните задания Онлайн тренажера Сравнение целых чисел
Сравнение отрицательных чисел, правило, примеры.
В этой статье мы разберем, как проводится сравнение отрицательных чисел. Здесь мы озвучим правило сравнения отрицательных чисел и рассмотрим применение этого правила при решении примеров.
Навигация по странице.
Правило сравнения отрицательных чисел
В основе сравнения отрицательных чисел (смотрите положительные и отрицательные числа) лежит сравнение модулей этих чисел. То есть, сравнение отрицательных чисел сводится к сравнению положительных чисел, равных модулям сравниваемых отрицательных чисел.
Данное правило сравнения отрицательных чисел относится как к целым числам, так и к рациональным числам и к действительным числам.
Из озвученного правила понятно, что на координатной прямой меньшее отрицательное число располагается левее, чем большее отрицательное число. Это утверждение, впрочем, справедливо для любых чисел, а не только для отрицательных.
Осталось рассмотреть примеры сравнения отрицательных чисел по данному правилу.
Примеры сравнения отрицательных чисел
Разберем решения нескольких примеров сравнения отрицательных чисел.
Начнем со сравнения двух отрицательных целых чисел. Это самый простой из возможных случаев сравнения отрицательных чисел, на нем проще всего усвоить суть правила сравнения отрицательных чисел.
Воспользуемся правилом сравнения отрицательных чисел. Оно нам указывает, что сначала нужно найти модули данных чисел, после чего провести сравнение полученных положительных чисел.
Немного сложнее дела обстоят со сравнением отрицательных рациональных чисел. Сравнение таких чисел сводится либо к сравнению обыкновенных дробей, либо к сравнению десятичных дробей.
Какое из отрицательных чисел 
и −3,7 больше?
Теперь можно перевести числа в обыкновенные дроби, после чего выполнить сравнение. Так смешанное число 
соответствует дроби 
, еще выполним перевод десятичной дроби в обыкновенную дробь: 
. Осталось выполнить сравнение обыкновенных дробей с разными знаменателями и 
. Приведем их к общему знаменателю: 
и 
, теперь видно, что 
, таким образом, 
. Следовательно, 
, откуда заключаем, что 
. То есть, из двух исходных отрицательных чисел большим является .
.
Сравнение отрицательных действительных чисел проводится по тому же правилу сравнения отрицательных чисел, примеры можно посмотреть в статье сравнение действительных чисел.
Сравнение отрицательных чисел: правило, примеры
В статье ниже озвучим принцип сравнения отрицательных чисел: сформулируем правило и применим его в решении практических задач.
Правило сравнения отрицательных чисел
В основе правила – сравнение модулей исходных данных. По сути, сравнить два отрицательных числа – значит сравнить положительные числа, равные модулям сравниваемых отрицательных чисел.
При сравнении двух отрицательных чисел меньшим является то число, модуль которого больше; бОльшим является то число, модуль которого меньше. Заданные отрицательные числа являются равными, если их модули равны.
Сформулированное правило применимо как к отрицательным целым числам, так и к рациональным и действительным.
Геометрическое толкование подтверждает принцип, озвученный в указанном правиле: на координатной прямой отрицательное число, которое является меньшим, находится левее, чем большее отрицательное. Это утверждение, в общем, верно для любых чисел.
Примеры сравнения отрицательных чисел
Самым простым примером сравнения отрицательных чисел является сравнение целых чисел. С подобной задачи и начнем.
Решение
Чуть сложнее сравнивать отрицательные рациональные числа: действие в конечном счете приводит к сравнению обыкновенных или десятичных дробей.
Решение
Также можно было осуществить сравнение путем перевода обыкновенной дроби в десятичную. Разница – лишь в удобстве вычисления.
Сравнение отрицательных действительных чисел производится согласно тому же правилу.
Отрицательные числа
Отрицательные числа — это числа со знаком минус (−), например −1, −2, −3. Читается как: минус один, минус два, минус три.
Примером применения отрицательных чисел является термометр, показывающий температуру тела, воздуха, почвы или воды. В зимнее время, когда на улице очень холодно, температура бывает отрицательной (или как говорят в народе «минусовой»).
Например, −10 градусов холода:
Обычные же числа, которые мы рассматривали ранее такие как 1, 2, 3 называют положительными. Положительные числа — это числа со знаком плюс (+).
При записи положительных чисел знак + не записывают, поэтому мы и видим привычные для нас числа 1, 2, 3. Но следует иметь ввиду, что эти положительные числа выглядят так: +1, +2, +3.
Координатная прямая
Координатная прямая это прямая линия, на которой располагаются все числа: и отрицательные и положительные. Выглядит следующим образом:
Здесь показаны только числа от −5 до 5. На самом деле координатная прямая бесконечна. На рисунке представлен лишь её небольшой фрагмент.
Числа на координатной прямой отмечают в виде точек. На рисунке жирная чёрная точка является началом отсчёта. Начало отсчёта начинается с нуля. Слева от начала отсчёта отмечают отрицательные числа, а справа — положительные.
Каждая точка на координатной прямой имеет своё имя и координату. Имя — это любая латинская буква. Координата — это число, которое показывает положение точки на этой прямой. Проще говоря, координата это то самое число, которое мы хотим отметить на координатной прямой.
Например, точка А(2) читается как «точка А с координатой 2« и будет обозначаться на координатной прямой следующим образом:
Здесь A — это имя точки, 2 — координата точки A.
Пример 2. Точка B(4) читается как «точка B с координатой 4« и будет обозначаться на координатной прямой так:
Пример 3. Точка M(−3) читается как «точка M с координатой минус три» и будет обозначаться на координатной прямой так:
Здесь M — это имя точки, −3 — координата точки M.
Точки можно обозначать любыми буквами. Но общепринято обозначать их большими латинскими буквами. Более того, начало отчёта, которое по другому называют началом координат принято обозначать большой латинской буквой O
Легко заметить, что отрицательные числа лежат левее относительно начала отсчёта, а положительные числа правее.
Сравнение отрицательных и положительных чисел
Правило 1. Любое отрицательное число меньше любого положительного числа.
Например, сравним два числа: −5 и 3. Минус пять меньше, чем три, несмотря на то, что пятёрка бросается в глаза в первую очередь, как цифра большая, чем три.
Связано это с тем, что −5 является отрицательным числом, а 3 — положительным. На координатной прямой можно увидеть, где располагаются числа −5 и 3
«Минус пять меньше, чем три»
Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.
Например, сравним числа −4 и −1. Минус четыре меньше, чем минус единица.
Связано это опять же с тем, что на координатной прямой −4 располагается левее, чем −1
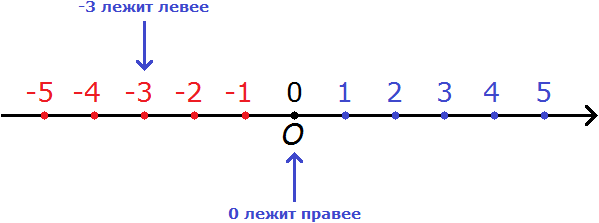
Правило 3. Ноль больше любого отрицательного числа.
Например, сравним 0 и −3. Ноль больше, чем минус три. Связано это с тем, что на координатной прямой 0 располагается правее, чем −3
Ноль больше, чем минус три
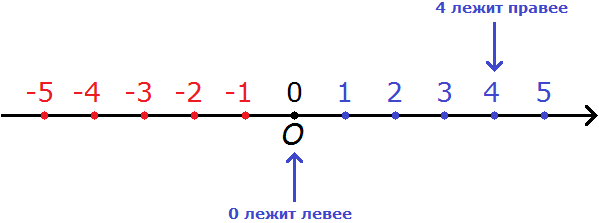
Правило 4. Ноль меньше любого положительного числа.
Например, сравним 0 и 4. Ноль меньше, чем 4. Это в принципе ясно и так. Но мы попробуем увидеть это воочию, опять же на координатной прямой:
Сравнение в математике — как определить, какие из чисел больше или меньше
Сравнение чисел — одна из самых легких и приятных тем из курса математики. Впрочем, нужно сказать, что она не так уж и проста. Например, мало кто испытывает трудности со сравнением однозначных или двузначных положительных чисел.
Но числа с большим количеством знаков уже вызывают проблемы, часто люди теряются при сравнении отрицательных чисел и не помнят, как сравнить два числа с разными знаками. На все эти вопросы мы и постараемся ответить.
Правила относительно сравнения положительных чисел
Начнем с самого простого — с чисел, перед которыми не стоит никакого знака, то есть с положительных.
Сравнение отрицательных чисел
Если у нас в задаче есть некие числа –а и –с, и нам нужно определить, какое из них больше, то применяется универсальное правило. Сначала выписываются модули этих чисел — |a| и |с| — и сравниваются между собой. То число, модуль которого больше, окажется меньшим в сравнении отрицательных чисел, и наоборот — большим числом будет то, модуль которого меньше.
Что делать, если сравнить нужно отрицательное и положительное число?
Здесь работает всего одно правило, и оно элементарно. Положительные числа всегда больше чисел со знаком «минус» — какими бы они ни были. Например, число «1» всегда будет больше числа «-1458» просто потому, что единица стоит справа от нуля на координатной прямой.
Также нужно помнить, что любое отрицательное число всегда меньше нуля.