какое определение потенциала электростатического поля справедливо
Общие сведения
Существует несколько видов взаимодействий. Например, гравитация определяется силой тяжести, а трение и упругость имеют электромагнитную природу. Изучает их электродинамика, одним из разделов которой является электростатика. Суть этой науки заключается в изучении взаимодействия зарядов, находящихся в неподвижном состоянии.
С физической точки зрения, любые тела влияют друг на друга. Между ними всегда действует сила притяжения. Но это явление незаметно из-за слабости существующих сил, связанной с массой тела. В 1600 году физик Уильям Гильберт, проводя эксперименты с янтарём, обнаружил, что если его потереть об шерсть, он начинает притягивать к себе лёгкие предметы. Им было обнаружено, что существует некая субстанция, с помощью которой можно описать новый вид взаимодействия. Получила она название «электростатическое поле».
Этот термин произошёл от слова «электрон», которое с греческого обозначает «янтарь». Было установлено, что в природе существуют силы, вызванные электрическим зарядом. Под ним решили понимать то, присутствие чего на телах вызывает их электростатическое взаимодействие. Сам же этот процесс назвали электризацией. Тела, способные взаимодействовать между собой, стали считать наэлектризованными.
В 1729 году член Парижской Академии наук Шарль Дюфе, изучая силы взаимодействия разных тел, установил, что существует два вида энергии. Один он получал при трении стекла о шёлк (стеклянный), а другой — смолы о шерсть (смоляной). В результате было установлено ключевое отличие возникающих сил от гравитационных. Первые обладали не только притяжением, но и отталкиванием.
Бенджамин Франклин предложил разделять существующие заряды по знаку на положительные и отрицательные. Таким образом, были сформулированы следующие природные свойства:
То есть при определённом действии, например, трении можно создать условия, при котором в телах произойдёт разделение зарядов, при этом величина их будет одинакова. Этот эффект назвали суперпозицией. Причём между разделёнными частицами возникает электростатическое поле, за энергетическую характеристику которой приняли потенциал.
Работа электростатического поля
Пусть имеется заряд, находящийся в электрическом поле. На него действует постоянная сила. Если носитель энергии перемещается из одной точки пространства в другую, то говорят о выполнении им работы. В простейшем случае можно рассмотреть однородное поле. В качестве него можно использовать конденсатор. В нём правая пластина пусть будет заряжена положительно, а левая — отрицательно.
Считается, что линии электрического поля будут направлены от плюса к минусу. В некоторой точке этого однородного состояния находится заряд. Для конкретики его можно принять положительным и обозначить буквой A. Под действием сил он перемещается в точку Б. Задача состоит в нахождении работы, совершаемой полем для изменения положения заряженной частицы.
Из механики известно, что такое действие может быть определенно произведением действующей на заряд силы и модуля перемещения, умноженным на косинус угла между ними: A = F * S * cos (a). Так как заряд положительный, то его направление будет совпадать с линиями электрического поля (напряжённостью E). Сила находится по формуле: F = q * E. Тогда, подставляя модуль этого вектора в выражение для работы, можно записать: A = q * E * S * cos (a).
Произведение S * cos (a) представляет собой проекцию отрезка перемещения на направление электрического поля. Изобразить её можно как перпендикуляр, опущенный на E. В результате получится прямоугольный треугольник. Обозначить прилежащий катет (проекцию) можно буквой d. В итоге формула для работы примет вид: A = q * E * d, где:
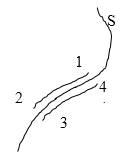
Пусть заряд перемещается по кривой. Например, проходит путь А-С-В. Значит, будет существовать два вектора S1 и S2. Тогда работа будет определяться как сумма A = Σ ΔAi. То есть если поле однородное (электростатическое), то работа по перемещению заряда не зависит от траектории, а определяется только начальным и конечным положением носителя заряда.
Таким свойством обладают силы тяжести и упругости. Называются они потенциальными. Следовательно, работа по перемещению электричества является такой же. Происходит она за счёт потенциальной энергии заряда, находящего в поле. Поэтому работа равняется уменьшению её значения. Выполненное действие пропорционально заряду, то есть отношению: W / q. Эта величина и получила название «электрический потенциал».
Свойства потенциала
Между находящимися частицами в электрическом поле существует напряжение. Оно равно отношению работы к числу заряда. Находят его по формуле: U = A / q. За единицу измерения напряжения принимают вольт. Обозначают его буквой В, характеризуется эта величина отношением джоуль на кулон. Так как разность потенциалов фактически является напряжением, то и измеряют её тоже в этих величинах.
Обозначают электрический потенциал буквой φ (фи). Он позволяет описывать электрическое поле, поэтому его называют энергетической характеристикой. Это скалярная величина. Определяется она как отношение потенциальной энергии заряда к его значению. В то же время напряжённость является силовой характеристикой. Так как эти два явления описывают одно и то же, то между ними существует связь.
Напряжённость позволяет определить силу, действующую на носитель энергии: E = F /q. Если вектор во всех точках пространства имеет одинаковое направление, то поле однородное. В нём на заряд действует сила F, определяемая как произведение заряда на вектор напряжённости. Пусть частица переместилась из А в В. Тогда она пройдёт расстояние d.
Совершённая работа будет определяться как A = q * E * d. Это то же, что A = U * q. Записанные выражения можно приравнять, причём сократить левую и правую часть на q. В результате получится связь между величинами: U = E * d. Так как напряжение — это разность потенциальности начальной и конечной точек, то формулу можно переписать так: φ1 — φ2 = E * d.
Отсюда можно сделать выводы:
Для понимания следует дать определение эквипотенциальной поверхности. За неё принимают пространство, во всех точках которого потенциал одинаков.
Решение задач
Для успешного решения заданий, связанных с электрическим потенциалом, нужно не только знать несколько формул, но и понимать суть явления. Кроме этого, часто приходится пользоваться справочником по электрофизике. Например, для выяснения массы зарядов.
Вот несколько типовых задач, рассчитанных на самостоятельную проработку учащимися в рамках школьной программы:
Таким образом, решать задачи, связанные с потенциалом, просто. Но при этом важно следить, в чём должны измеряться подставляемые величины. Все вычисления выполняют в Международной системе единиц (СИ).
Потенциальность электростатического поля
Потенциальное (консервативное) поле − это поле, в котором работа при перемещении зависит только лишь от конечной и начальной точки пути и не зависит от траектории движения тела.
Что такое потенциальное поле
Есть и другое абсолютно равнозначное определение потенциальности поля (консервативной силы).
Известно, что сила гравитации F G
На основе принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.
Легко докажем это математически. Циркуляция вектора напряженности поля точечного заряда E i → по любому замкнутому контуру равняется 0 :
Если поле создает N точечных зарядов, тогда по принципу суперпозиции результирующее поле находим как:
Что такое ротор. Практические задачи
Ротор − это вектор, проекция которого на направление единичного вектора n → определяется таким образом:
Обращаем внимание, что в формуле большой буквой S обозначена площадь, а маленькой буквой s − линейное перемещение.
Ротор описывает интенсивность «завихрения» вектора. На практике при вычислении ротора применяют следующие формулы:
Независимость работы от пути перемещения заряда в электростатическом поле выражается формулой:
где L 1 и L 2 − это различные пути между точками А и В . При замене местами пределов интегрирования получаем:
Выражение ∫ A L 1 B E → · d s → = ∫ A L 2 B E → · d s → представим в виде:
к уравнению выше, получаем:
Это дифференциальная формулировка потенциальности электростатического поля.
Необходимо найти r o t n υ → для точек оси вращения, если υ → − это вектор скорости точек твердого тела, вращающегося с угловой скоростью ω вокруг оси коллинеарной n →
Решение
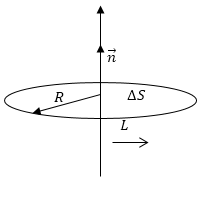
В качестве контура L выберем окружность радиусом R с центром на оси вращения, перпендикулярную оси (рисунок 1 ). Известно, что:
где ∮ d s = 2 π R − это длина окружности.
Необходимо доказать, что из условия потенциальности поля следует: тангенциальные составляющие напряженности электростатического поля непрерывны.
Решение
Поскольку электростатическое поле потенциально, тогда выполняется равенство:
Тангенциальные составляющие − это касательные к произвольной поверхности в любой ее точке. Непрерывность значит, что значения касательных составляющих напряженности одинаковы по обеим сторонам поверхности.
III. Основы электродинамики
Тестирование онлайн
Работа электростатического поля
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Потенциал

Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
Эту формулу можно представить в ином виде

Напряжение
Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
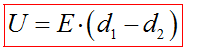
От величины напряжения зависит ток в цепи и энергия заряженной частицы.
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
Как определить знак потенциала
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.
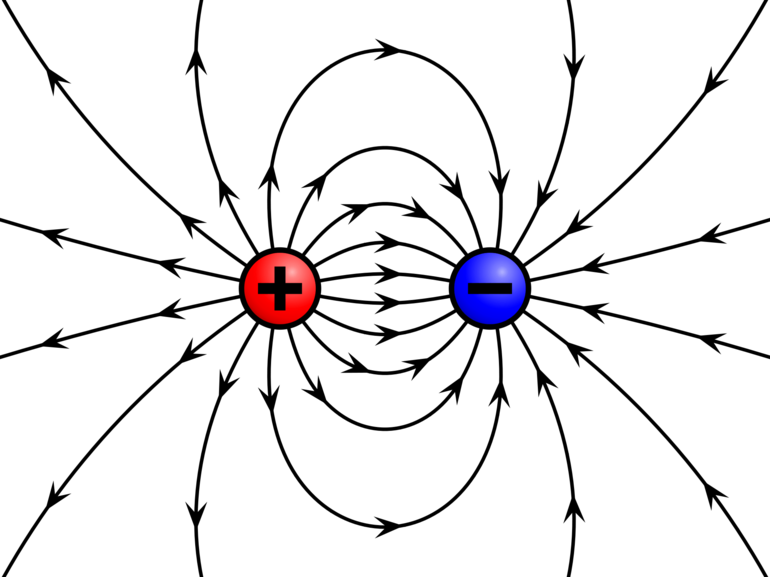
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу 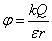
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
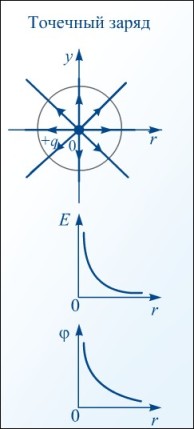
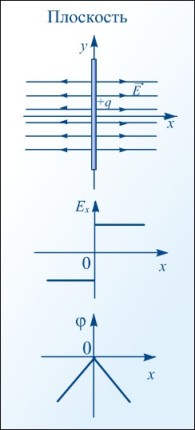
Зависимость напряженности и потенциала от расстояния
Потенциал поля, созданного равномерно заряженной сферой радиусом R и зарядом q на расстоянии r от центра сферы, равен
Напряжение в природе
Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В.
Напряжение в телефонных сетях может достигать 60 В.
Электрический угорь способен создавать напряжение до 650 В.
Энергия взаимодействия зарядов*
Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q1 и q2, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q2 из бесконечности в данную точку поля, созданного зарядом q1
Аналогично 
Какое определение потенциала электростатического поля справедливо
| Теорема о циркуляции вектора поля |   |
| Щелкните по ссылке » Потенциал и работа электростатического поля «, чтобы ознакомиться с презентацией раздела в формате PowerPoint. Для возврата к данной странице закройте окно программы PowerPoint. | |
В предыдущей теме было показано, что взаимодействие между покоящимися зарядами осуществляется через электростатическое поле. Описание электростатического поля мы рассматривали с помощью вектора напряженности Существует и другой способ описания поля – с помощью потенциала. Однако для этого необходимо сначала доказать, что силы электростатического поля консервативны, а само поле потенциально. Рассмотрим поле, создаваемое неподвижным точечным зарядом
где F(r)– модуль вектора силы Для того, чтобы доказать, что электростатическое поле потенциально, нужно доказать, что силы электростатического поля консервативны. Из раздела «Физические основы механики» известно, что любое стационарное поле центральных сил является консервативным, т.е. работа сил этого поля не зависит от формы пути, а только от положения конечной и начальной точек. Вычислим работу, которую совершает электростатическое поле, созданное зарядом q´ по перемещению заряда q из точки 1 в точку 2. Работа на пути dlравна: где dr – приращение радиус-вектора Тогда полная работа при перемещении q´ из точки 1 в точку 2 равна интегралу: Получили, что работа электростатических сил не зависит от формы пути, а только лишь от координат начальной и конечной точек перемещения. Следовательно, силы поля консервативны, а само поле – потенциально. Этот вывод можно распространить и на поле, созданное системой зарядов, так как по принципу суперпозиции полей: Итак, как и в механике, любое стационарное поле центральных сил является консервативными, т.е. работа сил этого поля не зависит от формы пути, а только от положения начальной и конечной точек. Именно таким свойством обладает электростатическое поле – поле, образованное системой неподвижных зарядов. Если в качестве пробного заряда, перенесенного из точки 1 (рис. 3.2) заданного поля Тогда вся работа равна: Такой интеграл по замкнутому контуру называется циркуляцией вектора Из независимости линейного интеграла от пути между двумя точками следует, что по произвольному замкнутому пути: Это утверждение и называют теоремой о циркуляции Для доказательства теоремы разобьем произвольно замкнутый путь на две части: 1а2 и 2b1 (рис. 3.2). Из сказанного выше следует, что (Интегралы по модулю равны, но знаки противоположны). Тогда работа по замкнутому пути: Поле, обладающее такими свойствами, называется потенциальным. Любое электростатическое поле является потенциальным.
| |
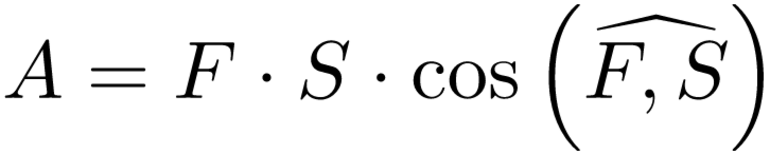






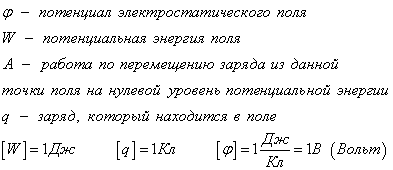

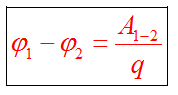
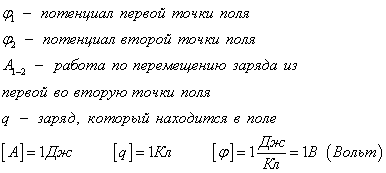


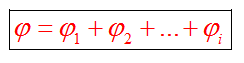





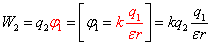

 , равного силе, действующей в данной точке на помещенный в неё пробный единичный положительный заряд
, равного силе, действующей в данной точке на помещенный в неё пробный единичный положительный заряд
 . В любой точке этого поля на пробный точечный заряд q действует сила
. В любой точке этого поля на пробный точечный заряд q действует сила  (рис. 3.1).
(рис. 3.1).
 ,
,  – единичный вектор, определяющий положение заряда q относительно q´, ε0 – электрическая постоянная.
– единичный вектор, определяющий положение заряда q относительно q´, ε0 – электрическая постоянная.
 при перемещении на dl;
при перемещении на dl;  т. е.
т. е.
 .
.

