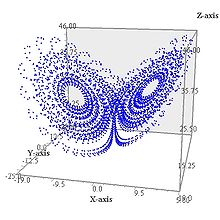
какое определение аттрактора является наиболее корректным
Аттрактор
Аттра́ктор (англ. attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. Аттрактором может являться притягивающая неподвижная точка (к примеру, в задаче о маятнике с трением о воздух), периодическая траектория (пример — самовозбуждающиеся колебания в контуре с положительной обратной связью), или некоторая ограниченная область с неустойчивыми траекториями внутри (как у странного аттрактора).
Существуют различные формализации понятия стремления, что приводит к различным определениям аттрактора, задающим, соответственно, потенциально различные множества (зачастую — вложенные одно в другое). Наиболее употребительными определениями являются максимальный аттрактор (зачастую — в своей малой окрестности, см. ниже), аттрактор Милнора и неблуждающее множество.
Аттракторы классифицируют по:
Также, есть известные «именные» примеры аттракторов: Лоренца, Плыкина, соленоид Смейла-Вильямса, гетероклинический аттрактор (пример Боуэна).
Содержание
Свойства и связанные определения
При всех определениях аттрактор полагается замкнутым и (полностью) инвариантным множеством.
С понятием аттрактора также тесно связано понятие меры Синая-Рюэлля-Боуэна: инвариантной меры на нём, к которой стремятся временные средние типичной (в смысле меры Лебега) начальной точки либо временные средние итераций меры Лебега. Впрочем, такая мера существует не всегда (что иллюстрирует, в частности, пример Боуэна).
Виды формализации определения
Поскольку всё фазовое пространство в любом случае сохраняется динамикой, формальное определение аттрактора можно давать, исходя из философии, что «аттрактор это наименьшее множество, к которому всё стремится» — иными словами, выкидывая из фазового пространства всё, что может быть выкинуто.
Максимальный аттрактор
Пусть для динамической системы задана область 
, которая переводится строго внутрь себя динамикой:
Тогда, максимальным аттрактором системы в ограничении на U называется пересечение всех его образов под действием динамики:
То же самое определение можно применить и для потоков: в этом случае, необходимо потребовать, чтобы векторное поле, задающее поток, на границе области было направлено строго внутрь неё.
У этого определения есть два недостатка. Во-первых, для его применения необходимо найти поглощающую область. Во-вторых, если такая область была выбрана неудачно — скажем, содержала отталкивающую неподвижную точку с её бассейном отталкивания — то в максимальном аттракторе будут «лишние» точки, около которых на самом деле несколько раз подряд оказаться нельзя, но текущий выбор области этого «не чувствует».
Аттрактор Милнора
По определению, аттрактором Милнора динамической системы называется наименьшее по включению замкнутое множество, содержащее ω-предельные множества почти всех начальных точек по мере Лебега. Иными словами — это наименьшее множество, к которому стремится траектория типичной начальной точки.
Неблуждающее множество
Точка x динамической системы называется блуждающей, если итерации некоторой её окрестности U никогда эту окрестность не пересекают:
0 \quad f^n(U)\bigcap U =\emptyset. » border=»0″ />
Иными словами, точка блуждающая, если у неё есть окрестность, которую любая траектория может пересечь только один раз. Множество всех точек, не являющихся блуждающими, называется неблуждающим множеством.
Статистический аттрактор
Статистический аттрактор определяется как наименьшее по включению замкнутое множество 
, в окрестности которого почти все точки проводят почти всё время: для любой его окрестности для почти любой (в смысле меры Лебега) точки 
выполнено
Минимальный аттрактор
Минимальный аттрактор определяется как наименьшее по включению замкнутое множество 
, в окрестности которого почти вся мера Лебега проводит почти всё время: для любой его окрестности выполнено
Примеры несовпадений
Локальность, минимальность и глобальность
Регулярные и странные аттракторы
Регулярные аттракторы
Притягивающая неподвижная точка
(пример: маятник с трением)
Предельный цикл
(пример: микрофон+колонки, осциллятор Ван дер Поля)
Странные аттракторы
(примеры: аттрактор Лоренца, аттрактор Рёсслера, соленоид Смейла-Вильямса; комментарий про эффект бабочки и про динамический хаос.)
Странный аттрактор — это аттрактор, имеющий два существенных отличия от обычного аттрактора: траектория такого аттрактора непериодическая (она не замыкается) и режим функционирования неустойчив (малые отклонения от режима нарастают). Основным критерием хаотичности аттрактора является экспоненциальное нарастание во времени малых возмущений. Следствием этого является «перемешивание» в системе, непериодичность во времени любой из координат системы, сплошной спектр мощности и убывающая во времени автокорреляционная функция.
Динамика на странных аттракторах часто бывает хаотической: прогнозирование траектории, попавшей в аттрактор, затруднено, поскольку малая неточность в начальных данных через некоторое время может привести к сильному расхождению прогноза с реальной траекторией. Непредсказуемость траектории в детерминированных динамических системах называют динамическим хаосом, отличая его от стохастического хаоса, возникающего в стохастических динамических системах. Это явление также называют эффектом бабочки, подразумевая возможность преобразования слабых турбулентных потоков воздуха, вызванных взмахом крыльев бабочки в одной точке планеты в мощное торнадо на другой её стороне вследствие многократного их усиления в атмосфере за некоторое время.
Среди странных аттракторов встречаются такие, хаусдорфова размерность которых отлична от топологической размерности и является дробной. Одним из наиболее известных среди подобных аттракторов является аттрактор Лоренца.
Именные примеры
Аттрактор Лоренца
Система диф. уравнений, создающих аттрактор Лоренца имеет вид:
при следующих значениях параметров: 
, 
, 
. Аттрактор Лоренца не является классическим, и даже не является странным в смысле Смейла. [2]
Соленоид Смейла-Вильямса
Соленоид Смейла-Вильямса — пример обратимой динамической системы, аналогичной по поведению траекторий отображению удвоения на окружности. Более точно, эта динамическая система определена на полнотории, и за одну её итерацию угловая координата удваивается; откуда автоматически возникает экспоненциальное разбегание траекторий и хаотичность динамики. Также соленоидом называют и максимальный аттрактор этой системы (откуда, собственно, и происходит название): он устроен как (несчётное) объединение «нитей», наматывающихся вдоль полнотория.
Аттрактор Плыкина
Пример Боуэна, или гетероклинический аттрактор
Аттрактор Эно
Гипотезы
Гипотеза Палиса
Гипотезы Рюэля
См. также
Примечания
Ссылки и литература
Полезное
Смотреть что такое «Аттрактор» в других словарях:
аттрактор — точка притяжения Словарь русских синонимов … Словарь синонимов
АТТРАКТОР — см. Синергетика. Большой психологический словарь. М.: Прайм ЕВРОЗНАК. Под ред. Б.Г. Мещерякова, акад. В.П. Зинченко. 2003 … Большая психологическая энциклопедия
Аттрактор — потенциальное состояние системы, к которому она эволюционирует. По Князевой: конечная область неминуемого схождения фазовых траекторий движения сложной системы. В качестве аттрактора может выступать или точка (устойчивый фокус), или иное более… … Словарь-справочник по философии для студентов лечебного, педиатрического и стоматологического факультетов
аттрактор — 3.1.1 аттрактор: Фактор саморазвития системы, влияющий на ее самоорганизацию и способность к взаимосодействию ее основных частей. Источник … Словарь-справочник терминов нормативно-технической документации
Аттрактор — (от лат. attraho притягиваю к себе) некоторая область, к которой притягиваются (сходятся) все возможные траектории движения систем … Начала современного естествознания
аттрактор — Syn: точка притяжения … Тезаурус русской деловой лексики
АТТРАКТОР — структура (функция), задающая (определяющая) устойчивое состояние любой системы. (См. синергетика, нелинейное мышление) … Философия науки: Словарь основных терминов
Аттрактор — (лат. притягиваю к себе) точка или множество точек (замкнутая кривая), к которому стремятся параметры состояния диссипативной системы, конечное состояние диссипативной системы (см. Система диссипативная) … Концепции современного естествознания. Словарь основных терминов
Аттрактор Рёсслера — Аттрактор Рёсслера хаотический аттрактор, которым обладает система дифференциальных уравнений Рёсслера … Википедия
Аттрактор Плыкина — пример динамической системы на диске, максимальный аттрактор которой гиперболичен. В частности, этот пример структурно устойчив, как удовлетворяющий аксиоме A Смейла. Конструкция Аттрактор Плыкина строится как фактор диффеоморфизма тора,… … Википедия
Теория хаоса
Что такое «странные аттракторы» и как они помогают синоптикам
Можно ли прогнозировать хаотическое движение элементов какой-либо системы? От чего зависит хаотическая динамика? Может ли, наконец, взмах крыла бабочки вызвать торнадо? Некоторые важные ответы на эти и другие вопросы нашел американский метеоролог Эдвард Лоренц, (невольный) автор термина «эффект бабочки» и создатель «странного аттрактора». Рассказываем об этом в первом материале, посвященном самым интересным дифференциальным уравнениям.
В 1972 году профессор метеорологии из Массачусетского технологического института Эдвард Лоренц собирался выступить на конференции, но в пылу работы не успел отправить тему своей лекции. Организатор, спешивший разослать приглашения, выбрал заголовок за него: «Предсказуемость: может ли взмах крыла бабочки в Бразилии вызвать торнадо в Техасе?» Так и появился термин «эффект бабочки», известный сегодня всему миру.
Эдвард Лоренц родился в 1917 году в небольшом городке в штате Коннектикут. Изучать атмосферные явления он решил еще в детстве, испытав потрясение от того, с какой легкостью солнечная погода может смениться бурей с громом и молниями.
Путь к исполнению мечты вышел долгим: магистратура в Гарварде, работа метеорологом в авиационном подразделении Армии США, защита диссертации в послевоенный период, наконец, должность научного сотрудника и, позже, профессора в MIT.
В своем выступлении Лоренц выделил несколько ключевых идей:
⦁ Если взмах крыла бабочки может вызвать торнадо, то точно так же на это способны все предыдущие и будущие взмахи, равно как и взмахи остальных миллионов бабочек, не говоря уже об активности бесчисленного населения нашей планеты.
⦁ Если взмах крыла бабочки способен вызывать торнадо, то в равной степени этот же взмах может его предотвратить.
Взмах крыла бабочки в данном контексте должен восприниматься как маленькое изменение начальных условий исследуемой системы, способное как вызвать торнадо, так и изменить его траекторию или вообще стать причиной его затухания.
В отличие от эффекта домино, где конкретное (обычно незначительное) действие приводит к конкретному (обычно значительному) результату, причем происходит это однозначно, взмах бабочки может не иметь никакого влияния на поведение торнадо.
Система Лоренца
Лоренц изучал конвекцию (теплообмен, возникающий за счет движения молекул жидкости или газа) в атмосфере Земли. Для описания подобных физических процессов часто пользуются моделью, которая включает в себя уравнения Навье-Стокса, описывающие движение вязкой ньютоновской жидкости (за исключением некоторых частных случаев, их решения в общем виде на данный момент неизвестны):
⦁ Уравнение движения в векторном виде:
⦁ Уравнение теплопроводности, описывающее распределение температуры в пространстве с течением времени:
⦁ Уравнение непрерывности, которое, по своей сути, описывает принцип сохранения массы чего-либо:
В оригинале эти три составляющие дают следующую систему:
Мы не будем углубляться в детальное объяснение всего вышеизложенного. Достаточно лишь понимать, что это довольно сложная модель, и Лоренцу в результате многостраничных выкладок удалось построить ее упрощение:
Здесь переменная с точкой сверху означает ее производную по времени. Более подробно:
С помощью этой системы уравнений можно рассчитать, как будет вести себя текучая среда, которую равномерно разогревают снизу и охлаждают сверху. Так, как это происходит с воздушными потоками в атмосфере. В частности, она позволяет понять, к какому результату приведет даже небольшое изменение исходных параметров.
Хаотическое движение
Перед тем как приступить к непосредственному анализу полученной системы, рассмотрим некоторые комбинации траекторий. Для наглядности, воспользуемся теми же значениями параметров, что и сам Лоренц: σ = 10, ρ = 28, β = 8/3.
Изобразим движение двух точек, расстояние между которыми изначально невелико:
Довольно интересный результат! Поначалу траектории почти неразличимы, потом они отклоняются совсем ненамного, после чего разница становится уже значительной.
Попробуем еще раз, однако теперь возьмем точки на значительном отдалении друг от друга:
Даже несмотря на подобную разницу начальных условий, траектории попадают на фигуру, которую впоследствии не покидают. Очень странно, их будто что-то притягивает…
Странный аттрактор Лоренца
Действительно, эта фигура так и называется — странный аттрактор Лоренца (от английского attract — «притягивать»).
Формальное математическое определение звучит так: аттрактор — такое подмножество фазового пространства, что все траектории, стартующие не слишком далеко от него, стремятся к нему с течением времени. (Это одно из возможных определений понятия аттрактора, существуют и другие, не эквивалентные данному.)
Слово же «странный» здесь выступает в таком ключе: аттрактор как множество не представим в виде кривой или поверхности, он имеет более сложную, фрактальную структуру. Траектории аттрактора не замыкаются, а малые отклонения постоянно накапливаются, причем экспоненциально.
Сказанное выше можно проиллюстрировать так: две траектории, выпущенные из близких точек, со временем разбегаются достаточно далеко. Причем, чтобы отдалить момент разбегания, например, на одну секунду, нужно уменьшить расстояние между начальными точками, скажем, вдвое. А чтобы на две секунды — вчетверо. А на три — в восемь раз, и так далее.
Это означает, что, даже используя мощный компьютер, мы не можем просчитать траекторию, проходящую вблизи аттрактора, с разумной точностью на протяжении длительного промежутка времени. На каждом шаге вычислений неизбежно вносятся ошибки (из-за округления чисел и погрешностей численных методов), которые быстро накапливаются и приводят к тому, что найденная траектория сильно отличается от настоящей.
Такое искажение невозможно исправить, просто увеличивая мощность компьютера. Подобное явление называется «динамическим хаосом».
Ниже представлена модель странного аттрактора, с которой можно поэкспериментировать, меняя входящие значения. Для желающих более подробно изучить математическую сторону припасен еще один раздел сразу после модели.
Вы можете покрутить модель или увеличить/уменьшить ее масштаб (с помощью кнопок мыши на десктопе или пальцами на экране смартфона). Значение бегунков сверху вниз:
Немного математики
Система Лоренца обладает несколькими замечательными свойствами:
⦁ Правая часть системы не имеет свободных членов, то есть она однородна.
Аттрактор
Аттра́ктор ( англ. attract — привлекать, притягивать) — множество состояний (точнее — точек фазового пространства) динамической системы, к которому она стремится с течением времени. Так, наиболее простыми вариантами аттрактора являются притягивающая неподвижная точка (к примеру, в задаче о маятнике с трением о воздух) и периодическая траектория (пример — самовозбуждающиеся колебания в контуре с положительной обратной связью), однако бывают и значительно более сложные примеры.
Существуют различные формализации понятия стремления, что приводит к различным определениям аттрактора, задающим, соответственно, потенциально различные множества (зачастую — вложенные одно в другое). Наиболее употребительными определениями являются максимальный аттрактор (зачастую — в своей малой окрестности, см. ниже), аттрактор Милнора и неблуждающее множество.
Аттракторы классифицируют по:
Содержание
Свойства и связанные определения [ ]
При всех определениях аттрактор полагается замкнутым и (полностью) инвариантным множеством.
С понятием аттрактора также тесно связано понятие меры Синая-Рюэлля-Боуэна : инвариантной меры на нём, к которой стремятся временные средние типичной (в смысле меры Лебега) начальной точки либо временные средние итераций меры Лебега. Впрочем, такая мера существует не всегда (что иллюстрирует, в частности, пример Боуэна ).
Виды формализации определения [ ]
Поскольку всё фазовое пространство в любом случае сохраняется динамикой, формальное определение аттрактора можно давать, исходя из философии, что «аттрактор это наименьшее множество, к которому всё стремится» — иными словами, выкидывая из фазового пространства всё, что может быть выкинуто.
Максимальный аттрактор [ ]
Пусть для динамической системы задана область U, которая переводится строго внутрь себя динамикой:
Тогда, максимальным аттрактором системы в ограничении на U называется пересечение всех его образов под действием динамики:
То же самое определение можно применить и для потоков: в этом случае, необходимо потребовать, чтобы векторное поле, задающее поток, на границе области было направлено строго внутрь неё.
У этого определения есть два недостатка. Во-первых, для его применения необходимо найти поглощающую область. Во-вторых, если такая область была выбрана неудачно — скажем, содержала отталкивающую неподвижную точку с её бассейном отталкивания — то в максимальном аттракторе будут «лишние» точки, около которых на самом деле несколько раз подряд оказаться нельзя, но текущий выбор области этого «не чувствует».
Аттрактор Милнора [ ]
По определению, аттрактором Милнора динамической системы называется наименьшее по включению замкнутое множество, содержащее ω-предельные множества почти всех начальных точек по мере Лебега. Иными словами — это наименьшее множество, к которому стремится траектория типичной начальной точки.
Неблуждающее множество [ ]
Точка x динамической системы называется блуждающей, если итерации некоторой её окрестности U никогда эту окрестность пересекают:
Иными словами, точка блуждающая, если у неё есть окрестность, которую любая траектория может пересечь только один раз. Множество всех точек, не являющихся блуждающими, называется неблуждающим множеством.
Статистический аттрактор [ ]
Статистический аттрактор определяется как наименьшее по включению замкнутое множество , в окрестности которого почти все точки проводят почти всё время: для любой его окрестности для почти любой (в смысле меры Лебега) точки выполнено
Минимальный аттрактор [ ]
Статистический аттрактор определяется как наименьшее по включению замкнутое множество , в окрестности которого почти вся мера Лебега проводит почти всё время: для любой его окрестности выполнено