какое название придумали для сотой части величины числа
Проценты. Нахождения процентов от числа
На практике люди часто пользуются сотыми частями величин. Например, сотая часть гектара − 1 ар ( 1 сотка), сотая часть века − 1 год, сотая часть рубля − 1 копейка, сотая часть метра − 1 сантиметр.
Для сотой части величины или числа придумали специальное название − один процент (от лат. pro centum − «на сто») и обозначение − 1 %.
Например, 1 % от 300 кг равен 3 кг. Действительно, 300 кг : 100 = 3 кг.
Например, если говорят, что работа выполнена на 100 %, то выполнена вся работа; если турист прошел 100 % маршрута, то он прошел весь маршрут.
Если мы хотим показать, как изменилась величина, то это можно сделать с помощью процентов.
Например, если спортивную секцию посещали 12 учащихся, а стали посещать 24, то говорят, что количество членов секции увеличилось на 100 %. Если во время новогодней распродажи мобильный телефон стал стоить в два раза дешевле, то говорят, что его цена снизилась на 50 %.
Вообще, если величина стала в два раза больше, то она увеличилась на 100 % (рис. 211 ),
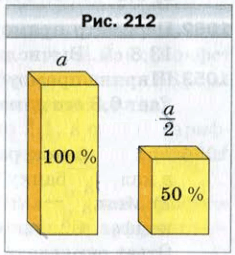
а если величина стала в два раза меньше, то она уменьшилась на 50 % (рис. 212 ).
Также можно выполнить обратное преобразование, т. е. записать десятичную дробь или натуральное число в процентах. Для этого нужно число умножить на 100 и к результату приписать знак %.
Например, 1,4 = 140 %; 0,02 = 2 %; 7 = 700 %.
Часто для того, чтобы иметь более точное представление о величине, удобно выразить ее в процентах. Предположим, что ты в этом полугодии получил девять пятерок по математике − это много или мало? Ответить на этот вопрос нельзя, ведь неизвестно, сколько всего оценок по математике ты получил в этом полугодии и какую часть из них составляют пятерки. А вот если сказать, что в этом полугодии из твоих оценок по математике 90 % − пятерки, то сразу становится понятным: ты очень хорошо знаешь этот предмет.
1 ) 15 : 100 = 0,15 (кг) − составляет 1 % массы всей клубники.
2 ) 0,15 * 6 = 0,9 (кг) − сахара содержится в 15 кг клубники.
Рассмотрим еще две подобные задачи.
1 ) 40 + 25 = 65 (%) − составляют конфеты и печенье.
2 ) 100 − 65 = 35 (%) − составляет мармелад.
3 ) 600 : 100 = 6 (кг) − составляет 1 % массы завезенного товара.
4 ) 6 * 35 = 210 (кг) − завезли мармелада.
1 ) 45 000 : 100 = 450 (р.) − составляет 1 % вклада.
2 ) 450 * 9 = 4050 (р.) − будет начислено процентных денег на конец года.
3 ) 45 000 + 4 050 = 49 050 (р.) − станет на счете через год.
1 ) 45 000 : 100 = 450 (р.) − составляет 1 % вклада.
2 ) 100 + 9 = 109 (%) − исходный суммы составят деньги на счете на конец года.
3 ) 450 * 109 = 49 050 (р.) − станет на счете через год.
Математика. 6 класс
Конспект урока
Десятичные дроби и проценты. Часть 1
Перечень рассматриваемых вопросов:
Процент – это сотая часть величины.
Вся величина – это сто процентов (100 %).
Теоретический материал для самостоятельного изучения
Люди часто используют сотые части величин, например, сотая часть центнера – это килограмм, сотая часть века – год, сотая часть метра – сантиметр и так далее. Для сотой части любой величины придумали специальное название – один процент, и обозначение – 1%.
Так как процент – это сотая часть величины, то для того, чтобы найти один процент от величины, нужно её значение разделить на 100.
Заметим, что 100 процентов величины это 100 сотых величины, то есть 100 процентов величины – это вся величина, или целое.
Чтобы перевести десятичную дробь в проценты, надо её умножить на 100.
0,023 = 0,023 · 100 % = 2,3 %
Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.
В начале ученого года вы научились решать простые задачи на проценты с помощью пропорции. Например:
12 % от числа составляют 60. Найдите целое число.
Целое число это 100 %. Запишем данные.
Перед нами прямая пропорциональность, составим пропорцию.
Теперь вы умеете умножать и делить на десятичную дробь, и решать задачи на проценты сможете и другим способом.
Рассмотрим задачи основных типов. Первый тип – это нахождение процентов данного числа.
Задача. Найти 15 процентов от 70 метров.
Решение. 15 процентов – это 15 сотых. То есть нужно найти 0,15 от 70. Помним, что для того, чтобы найти дробь от числа, надо число умножить на эту дробь.
Получим, что 15 процентов от 70 метров это 10,5 метров.
Ответ: 15 % от 70 метров это 10,5 метров.
Второй тип задач – нахождение числа по его процентам.
Задача. Найти число, если 30 процентов этого числа составляют 60.
Решение. Запишем 30 процентов в виде десятичной дроби, это 0,3.
Чтобы найти целое по его части, нужно часть разделить на соответствующую ей дробь.60 разделить на 0,3 десятых получим 200.
Ответ: целое число это 200.
Третий тип задач. Найти, сколько процентов составляет одна величина от другой.
Задача. Сколько процентов составляет число 6 от 16?
Решение. Чтобы ответить на этот вопрос, нужно сначала выяснить, какую часть составляет число 6 от числа 16. Для этого нужно 6 разделить на 16.
Запишем в виде обыкновенной дроби и сократим её.
И затем умножим на 100 процентов.
Получим 37,5 десятых процентов.
Ответ: число 6 от числа 16 составляет 37,5 %.
Разбор заданий тренировочного модуля
Тип 1. Подстановка элементов в пропуски в тексте.
Впишите верное число.
Решение. Переведём обыкновенную дробь в десятичную.
Теперь переведём десятичную дробь в проценты, умножив её на 100.
Тип 2. Подстановка элементов в пропуски в тексте
Впишите пропущенное число.
Закрашено …% площади квадрата.
Решение. Вся площадь квадрата – это 36 клеток. Закрашено 9 клеток. Значит, чтобы найти, сколько процентов закрашено, нужно 9 разделить на 36 и частное умножить на 100 %. Получаем
Математика. 6 класс
Конспект урока
Десятичные дроби и проценты. Часть 1
Перечень рассматриваемых вопросов:
Процент – это сотая часть величины.
Вся величина – это сто процентов (100 %).
Теоретический материал для самостоятельного изучения
Люди часто используют сотые части величин, например, сотая часть центнера – это килограмм, сотая часть века – год, сотая часть метра – сантиметр и так далее. Для сотой части любой величины придумали специальное название – один процент, и обозначение – 1%.
Так как процент – это сотая часть величины, то для того, чтобы найти один процент от величины, нужно её значение разделить на 100.
Заметим, что 100 процентов величины это 100 сотых величины, то есть 100 процентов величины – это вся величина, или целое.
Чтобы перевести десятичную дробь в проценты, надо её умножить на 100.
0,023 = 0,023 · 100 % = 2,3 %
Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.
В начале ученого года вы научились решать простые задачи на проценты с помощью пропорции. Например:
12 % от числа составляют 60. Найдите целое число.
Целое число это 100 %. Запишем данные.
Перед нами прямая пропорциональность, составим пропорцию.
Теперь вы умеете умножать и делить на десятичную дробь, и решать задачи на проценты сможете и другим способом.
Рассмотрим задачи основных типов. Первый тип – это нахождение процентов данного числа.
Задача. Найти 15 процентов от 70 метров.
Решение. 15 процентов – это 15 сотых. То есть нужно найти 0,15 от 70. Помним, что для того, чтобы найти дробь от числа, надо число умножить на эту дробь.
Получим, что 15 процентов от 70 метров это 10,5 метров.
Ответ: 15 % от 70 метров это 10,5 метров.
Второй тип задач – нахождение числа по его процентам.
Задача. Найти число, если 30 процентов этого числа составляют 60.
Решение. Запишем 30 процентов в виде десятичной дроби, это 0,3.
Чтобы найти целое по его части, нужно часть разделить на соответствующую ей дробь.60 разделить на 0,3 десятых получим 200.
Ответ: целое число это 200.
Третий тип задач. Найти, сколько процентов составляет одна величина от другой.
Задача. Сколько процентов составляет число 6 от 16?
Решение. Чтобы ответить на этот вопрос, нужно сначала выяснить, какую часть составляет число 6 от числа 16. Для этого нужно 6 разделить на 16.
Запишем в виде обыкновенной дроби и сократим её.
И затем умножим на 100 процентов.
Получим 37,5 десятых процентов.
Ответ: число 6 от числа 16 составляет 37,5 %.
Разбор заданий тренировочного модуля
Тип 1. Подстановка элементов в пропуски в тексте.
Впишите верное число.
Решение. Переведём обыкновенную дробь в десятичную.
Теперь переведём десятичную дробь в проценты, умножив её на 100.
Тип 2. Подстановка элементов в пропуски в тексте
Впишите пропущенное число.
Закрашено …% площади квадрата.
Решение. Вся площадь квадрата – это 36 клеток. Закрашено 9 клеток. Значит, чтобы найти, сколько процентов закрашено, нужно 9 разделить на 36 и частное умножить на 100 %. Получаем
Процент, сотая часть числа
Смотреть что такое «Процент, сотая часть числа» в других словарях:
Процент сотая часть числа — Если, например, в городе 45 тысяч жителей, то 450 человек составляют один П. населения. Предположим, что на какое нибудь предприятие истрачено 20 тыс. руб. и чистого дохода получено 3 тыс. руб. В этом случае доход составляет 15/100 частей… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ПРОЦЕНТ — сотая часть числа, принимаемого за единицу; обозначается знаком % … Большая политехническая энциклопедия
ПРОЦЕНТ — (лат.). Цифра, означающая прибыль или плату с сотни. В химии: выраженное в числах отношение различных составных частей вещества. В статистике: отношение народонаселения и т. д. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А … Словарь иностранных слов русского языка
Процент — % Процент (лат. per cent на сотню) одна сотая доля. Обозначается знаком «%». Используется для обозначения доли чего либо по отношению к целому. Например, 17 % от 500 кг означает 17 частей по 5 кг каждая, то есть… … Википедия
ИНВЕСТИРОВАНИЕ — INVESTINGПод И. понимается вложение капитала с целью получения прибыли. Ожидаемая прибыль может быть в виде дивидендов, процентов или увеличения реального капитала. Попытка извлечь выгоду из кратковременных изменений стоимости актива называется… … Энциклопедия банковского дела и финансов
Автомат Калашникова — У этого термина существуют и другие значения, см. Автомат Калашникова (значения). Автомат Калашникова … Википедия
Десятичные дроби
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)