какое наибольшее количество коней можно расставить на шахматной доске чтобы они не били друг друга
Какое наибольшее количество коней можно расставить на шахматной доске чтобы они не били друг друга
а) Какое максимальное количество слонов можно расставить на доске 1000 на 1000 так, чтобы они не били друг друга?
б) Какое максимальное количество коней можно расставить на доске 8×8 так, чтобы они не били друг друга?
Решение
а) Поскольку на одной диагонали не может стоять больше одного слона, а всего диагоналей, идущих снизу-слева направо-вверх, ровно 1999, причём на двух крайних (состоящих из одной клетки) может стоять не больше одного слона (они расположены на одной перпендикулярной диагонали), то на доску нельзя поставить больше 1998 не бьющих друг друга слонов.
Это число достигается: например, можно поставить 1000 слонов на верхний ряд доски и 998 слонов – на нижний ряд, кроме угловых клеток.
б) 32 коня можно поставить на все белые клетки.
Разобьём доску на 8 прямоугольников 4×2, а каждый из них – на четыре пары клеток, соединённых ходом коня. Всего получилось 32 пары, и в каждой из них может стоять не более одного коня.
Ответ
а) 1998 слонов; б) 32 коня.
Источники и прецеденты использования
| Кружок | |
| Название | ВМШ 57 школы |
| класс | |
| Класс | 7 |
| год | |
| Год | 2001/02 |
| Место проведения | 57 школа |
| занятие | |
| Номер | 6 |
| Название | На шахматной доске |
| Тема | Неопределено |
| задача | |
| Номер | 02 |
Какое наибольшее количество коней можно расставить на шахматной доске чтобы они не били друг друга
Может ли произведение цифр трёхзначного числа быть равно 22? 28? 350? 730?
Может ли и сумма, и произведение нескольких натуральных чисел (не обязательно различных) быть равными а) 999? б) 1999?
Площадь прямоугольника меньше 1 кв.м. Может ли его периметр быть больше 1 км?
Фирма проработала год, подсчитывая свою прибыль каждый месяц. За каждые два подряд идущих месяца прибыль оказалась отрицательна (то есть фирма заработала меньше чем потратила). а) Могло ли случиться, что прибыль за весь весь год оказалась положительна? б) А за первые 11 месяцев?
В однокруговом футбольном турнире за победу давали 2 очка, за ничью 1 очко, за поражение 0 очков. «Спартак» одержал больше всех побед. Мог ли он набрать меньше всех очков?
Можно ли на шахматной доске расставить а) 9 ладей; б) 14 слонов так, чтобы они не били друг друга?
б) Можно. Например, так.
Какое наибольшее число ладей (слонов, королей, ферзей, коней) можно расставить на доске так, чтобы они не били друг друга?
Новые задачи. Разнобой.
188. Можно ли числа от 1 до 17 выписать по кругу так, чтобы сумма любых двух соседних чисел была простым числом?
189. Как посадить 9 деревьев так, чтобы получилось 10 прямых рядов по три дерева в каждом?
190. Во фразе, взятой в кавычки, подставьте вместо многоточий числа так, чтобы она оказалась верной.
191. Два человека бегут вниз по ступеням эскалатора метро, идущего вниз. Один бежит быстрее другого. Кто из них насчитает больше ступенек?
192. В квадрате 3 x 3 находится 9 лампочек. За одну операцию можно переключить все лампочки, находящиеся в каком-нибудь квадрате 2 x 2. Сколько различных узоров можно получить из погасшего» состояния?
193. Можно ли в вершинах и на серединах сторон правильного восьмиугольника расставить натуральные числа от 1 до 16 так, чтобы сумма чисел на концах любой стороны равнялась числу в его середине? Каждое из чисел можно использовать ровно 1 раз.
195. На доске выписаны целые числа от 1 до 14, каждое по одному разу. Двое играющих по очереди стирают по одному числу до тех пор, пока не останется ровно два числа. Если их сумма точный квадрат, то выигрывает второй, иначе первый. Кто выигрывает при правильной игре?
Задача о конях. «Какое максимальное количество коней можно расставить на шахматной доске так, чтобы они не били друг друга».
Страницы работы
Содержание работы
Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра прикладной математики и информатики
Лабораторная работа №2
Факультет: ПМИ
Студенты: Голубева М. В.
Преподаватели: Пономаренко В.М.
Задача о конях. «Какое максимальное количество коней можно расставить на шахматной доске так, чтобы они не били друг друга».
1. Сформулировать задачу в закрытой форме. Выбрать комбинацию из следующих подходящих стратегий решения задачи:
— представление в пространстве состояний;
— сведения задач к подзадачам;
— генерация вариантов и проверка;
— поиск в глубину с возвратом;
— поиск с предпочтением (эвристический поиск),
— сведение задачи к доказательству теоремы.
2. Разработать адекватную структуру данных, максимально учитывающую специфику предметной области задачи. Обосновать выбор структуры.
5. Выделить пространство состояний и нарисовать граф переходов.
6. Привести интерпретацию программы с точки зрения декларативной и процедурной семантик.
Сформулируем преложенную задачу в терминах пространства состояний:
Алгоритм решения задачи – поиска в глубину.
Наглядно пространство состояний может быть представлено в виде:
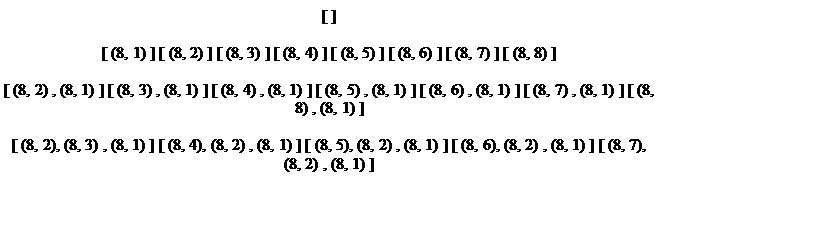
Алгоритм поиска решения полнопереборный и с увеличением числа коней, которых необходимо расставить на доске, количество перебираемых вариантов сильно возрастает.
Максимальное число коней, которых можно разместить на доске 8х8, составляет 32.
Правильный алгоритм расстановки коней(имеется ввиду самый эффективный) заключается в том, чтобы расставлять так, чтобы по вертикали и по горизонтали кони были друг от друга через одну, а соседствовали только по диагонали.
Аналогично тому, как это было сделано для задачи о восьми ферзях в книге
“И.Братко Программирование на языке ПРОЛОГ для искусственного интеллекта”, для реализации алгоритма сформулируем необходимые условия
Для отношения решение
a) Кони, перечисленные в списке остальные не должны бить друг друга, т.е. сам список oстальные должен являться решением.
b) X и Y должны быть целыми числами от 1 до 8 (доска 8х8)
c) Конь, стоящий на поле X\Y, не должен бить ни одного коня из списка остальные.
Если список коней пуст то он является решением.
Добавим однако еще в предикат решение в качестве параметра количество коней которых еще надо разместить на доске.
Небьет(Х, Y, остальныеХ, остальныеY).
Теперь определим отношение небьет(Х, Y, СписХ, СписY)
Здесь список СписХ = [Х1|СписХ1] Спис =[Y1|СписY]
a) Если список пуст то отношение выполнилось т.к. некого бить
b) Если список не пуст то должно выполняться что
· Х/Y не должен бить ни одного коня из списка остальные
· Х/Y не должен бить Х1/Y1
Данные условия выражаются следующим предикатом
Предикат бьет() просто проверяет не выполняется какая-нибудь из следующих ситуаций
write(«Choose 1 to set number of knights.»),nl,
write(«Choose 2 to use the best strategy from the begining.»),nl,
write(«Enter number of Knights : «),
write(«The best strategy is to set knights in 1!»),nl,
Миролюбивые шахматные кони
Задача
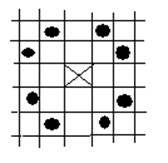
Клетки доски 5×5 раскрашены в шахматном порядке (рис. 1). а) Какое наибольшее число шахматных коней можно расставить на этой доске так, чтобы они не били друг друга? б) Сколькими способами это можно сделать?
Подсказка
Кони, стоящие на одной диагонали, друг друга не бьют.
В пункте б) ответ — один способ. Но это надо доказать.
Решение
Расстановка 13 коней показана слева на рис. 2. Докажем, что большее число не бьющих друг друга коней расставить на такой доске нельзя. Для этого мысленно разобьем клетки на пары так, чтобы в каждую пару входили клетки, отстоящие друг от друга на один ход коня. Одной клетке, естественно, пары не найдется. В том, что такое разбиение существует, можно убедиться, посмотрев на правую часть рис. 2.
Очевидно, что, как ни расставляй коней на доске, в каждой паре можно будет занять не больше одной клетки. Это означает, что коней заведомо не больше, чем количество пар, которых 12, плюс один (одна непарная клетка) — то есть 13.
Чтобы показать, что расстановка 13 коней на этой доске всего одна, идею с разбиением клеток на пары удобно несколько модифицировать.
Рассмотрим граф, вершинами которого будут центры клеток доски. Две вершины соединим ребром, если из одной в другую можно попасть за один ход коня. Этот граф показан слева на рис. 3. Важно, что в этом графе есть последовательность ребер, которая проходит через каждую из 25 вершин ровно по одному разу (рис. 3, справа).
На языке теории графов последовательности вершин, соединенных по цепочке ребрами, называют путями. Ясно, что из любых двух клеток, которые встречаются подряд на нашем пути, конь может стоять только в одной. Поэтому для того, чтобы «уместить» максимальное число коней, начинать надо прямо с первой клетки этого пути. Это и даст расстановку, показанную на рис. 2.
Послесловие

Рис. 4. Уильям Гамильтон, фотопортрет середины XIX века. Изображение из твиттера библиотеки Дублинского университета
Путь в графе, который помог нам решить задачу, проходил через все вершины графа по одному разу. Такие пути называются гамильтоновыми. Если в графе есть замкнутый гамильтонов путь (у которого совпадают начало и конец, путь в таком случае является циклом), то сам граф называется гамильтоновым. Название дано в честь ирландского математика Уильяма Гамильтона (1805–1865), которого по праву называют одним из величайших математиков XIX столетия: он оставил значительный вклад в разных областях математики (про некоторые важнейшие разделы вообще можно сказать, что они впоследствии выросли из его работ), механики и оптики.
Известно, что по мотивам своих исследований Гамильтон даже придумал игру-головоломку «Икосиан» (осторожно: перейдя по этой ссылке вы увидите решение головоломки!), которая одно время продавалась и была довольно популярной. Цель игры — построить гамильтонов цикл (то есть пройти по всем вершинам, каждый раз переходя в соседнюю по ребру, и вернуться в начало пути) в правильном додекаэдре (рис. 5, слева). Поскольку изготавливать такой правильный многогранник, а затем распространять его и, главное, играть с ним не очень удобно, игра представляла собой плоскую доску с выемками для фишек, соединенными линиями, соответствовавшими ребрам додекаэдра (рис. 5, справа). Фишек было 20 (столько же, сколько вершин у додекаэдра), они были пронумерованы, чтобы их можно было расставлять в порядке обхода.
Рис. 5. Слева: додекаэдр — один из пяти правильных многогранников; у него 12 граней, являющихся одинаковыми правильными пятиугольниками, 30 ребер и 20 вершин. Рисунок с сайта ru.wikipedia.org. Справа: оригинальный экземпляр игры «Икосиан». Любопытно, что игра названа «в честь» икосаэдра, а обходить в ней надо додекаэдр. Связано это с тем, что эти два многогранника двойственны друг другу Фото с сайта researchgate.net
В задаче о гамильтоновом пути требуется выяснить, есть ли в данном графе гамильтонов путь (или цикл), и, в случае положительного ответа, найти его явно. Эта задача — важная и неожиданно сложная с точки зрения сложности вычислений: в известных алгоритмах с ростом числа вершин в графе количество требуемых операций растет экспоненциально. Из-за этого такие алгоритмы на практике неэффективны: фактически для произвольного графа с сотней-другой вершин уже невозможно получить ответ на этот вопрос даже на самом мощном суперкомпьютере. По сути, эти алгоритмы — хоть и оптимизированный, но перебор всех возможных путей.
При этом, если кто-нибудь предоставит вам сколь угодно большой и сложный граф, а также путь в нем, то проверить, является ли этот конкретный путь гамильтоновым, вы сможете довольно просто. Это (вместе с тем, что пока неизвестен быстрый алгоритм решения) означает, что с точки зрения теории алгоритмов задача о гамильтоновом пути попадает в класс сложности NP. Более того, она является NP-полной задачей: к ней относительно просто — за полиномиальное время — можно свести любую другую задачу из этого класса. Раз уж зашла речь об классах сложности, то нельзя не упомянуть одну из так называемых задач тысячелетия — проблему равенства классов P и NP. К классу P относятся задачи, для которых известны алгоритмы, в которых количество операций растет как какой-то определенный многочлен от размера входных данных. Даже если степень многочлена большая, с точки зрения теории алгоритмов такая задача считается простой. Если придумать полиномиальный алгоритм для любой NP-полной задачи (в том числе и для поиска гамильтонова пути), то эта проблема автоматически будет решена.
При этом с «теоретической» точки зрения про гамильтоновы пути известно, грубо говоря, всё, поскольку теорема Бонди — Хватала (Bondy–Chvátal theorem) дает критерий того, что граф является гамильтоновым: для этого необходимо и достаточно, чтобы замыкание этого графа тоже было гамильтоновым графом. Замыкание графа G с n вершинами — это граф, который строится последовательным «пририсовыванием» ребер, соединяющих любую пару вершин, удовлетворяющую следующим двум свойствам: во-первых, эти вершины должны быть еще не соединены ребром, а во-вторых, сумма их степеней должна быть больше n. Проблема с этой теоремой в том, что она не помогает в алгоритмическом поиске гамильтонова цикла. И даже просто для ответа на вопрос о том, есть ли в графе такой цикл, она плохо годится, поскольку сводит проверку одного графа к проверке другого, в котором к тому же больше ребер. Исключение — те случаи, когда замыкание графа оказывается «хорошим»: про него относительно легко понять, что он гамильтонов. Пример «хорошего» в этом смысле графа — полный граф, в котором любые две вершины соединены ребрами (при \(n>2\) он точно гамильтонов).

Рис. 6. Леонард Эйлер. Портрет, выполненный Я. Э. Хандманном (1756 год). Рисунок с сайта ru.wikipedia.org
Кстати, с другим важным типом путей в графах — эйлеровыми путями, которые проходят по одному разу по всем ребрам, — все гораздо проще. Во-первых, есть простой критерий эйлеровости графа: связный граф эйлеров (то есть в нем есть эйлеров цикл) тогда и только тогда, когда в нем нет вершин нечетной степени. Во-вторых, есть алгоритмы, которые ищут такие пути за линейное время от размера графа (количества ребер). Понятие эйлерова пути появилось, когда Леонард Эйлер размышлял над задачей о семи кёнигсбергских мостах (это было в районе 1736 года).
Охватить весь спектр приложений эйлеровых и гамильтоновых графов в рамках нашей статьи невозможно, но можно посоветовать заинтересовавшимся читателям ознакомиться, например, со статьей Ф. Компо и П. Певзнера «Реконструкция генома: головоломка из миллиарда кусочков» («Квант», №3 за 2014 год). В ней подробно описано, какие математические идеи лежат в основе методов секвенирования ДНК и, в том числе, какую роль играют в этом эйлеровы и гамильтоновы графы.
Вернемся к приключениям шахматного коня на доске. Вспомним, что в решении задачи мы рассмотрели «коневой» граф шахматной доски 5×5 (он нарисован слева на рис. 3) и нашли в нем гамильтонов путь. По сути, этот путь показывает, как можно шахматным конем обойти всю доску, побывав в каждой клетке ровно один раз. Оказывается, этот вопрос — можно ли обойти конем данную доску (не обязательно квадратную)? — известен не одну сотню лет. Распространенное название — задача о ходе коня (Knight’s tour).
Легко видеть (на примере нашей задачи), что это частный случай поиска гамильтонова пути. Благодаря специфике «коневого» графа он решается относительно просто. Одно из первых исследований этого вопроса, кстати, выполнил Эйлер: в статье Solution d’une question curieuse qui ne paroît soumise à aucune analyse (1759 год) он предложил способ строить нужные обходы коня для доски 8×8.
С тех пор, разумеется, этот вопрос изучен вдоль и поперек. Например, известно, что всего для обычной шахматной доски существует 13 267 364 410 532 замкнутых обходов. Придуманы разные алгоритмы построения нужного пути. Самый, пожалуй, простой формулируется буквально одной фразой: нужно начать из любой клетки и каждым ходом ходить в ту клетку, с которой потом можно попасть на минимальное число еще не пройденных клеток (если таких клеток несколько, то можно выбрать любую). Этот способ называется правилом Варнсдорфа, он был предложен еще в XIX веке. Уточнение, написанное в скобках, делать приходится, потому что описанные в нем ситуации вполне вероятны и нужно хоть как-то выбирать из равнозначных вариантов. При внимательном исследовании этого способа (уже при помощи компьютеров) оказалось, что иногда совсем произвольный выбор следующей клетки для хода коня может впоследствии завести его в тупик. Однако это происходит довольно редко. Подробнее об этом рассказано в книге Е. Гика «Шахматы и математика».
Наконец, приведем еще пару задач, в которых рассмотренные выше идеи помогают найти решение без перебора.
1. Можно ли выписать целые числа от 0 до 9 в таком порядке, чтобы сумма любых двух соседних чисел делилась либо на 5, либо на 12? (Использовать каждое число можно только один раз.)
Построим граф, в котором вершины соответствуют данным числам. Соединим две вершины ребром, если сумма соответствующих чисел делится либо на 5, либо 12. После этого остается найти в таком графе гамильтонов путь.
2. Мышь грызет кусок сыра в форме куба 3×3×3, разбитый на единичные кубики. Когда она съедает один кубик целиком, то приступает к соседнему по грани кубику. Может ли она таким образом съесть всё, кроме центрального кубика?
Идея в том, чтобы раскрасить единичные кубики в шахматном порядке. Тогда в любом «пути» мышки по кубикам их цвета будут чередоваться. Значит, число «белых» кубиков не может отличаться от числа «черных» больше чем на 1.
3. Картинная галерея имеет форму правильного треугольника, который разбит на 36 одинаковых треугольных залов (залы — тоже правильные треугольники). Между любыми двумя соседними залами есть дверь. Какое наибольшее число залов может обойти, если не заходить в один и тот же зал дважды?
Подробный разбор этих задач, другие примеры и более строгое обсуждение их математической сути можно найти в статье П. Кожевникова «Длинные пути в графах» («Квант», №1 за 2018 год).
| Главная ≫ Инфотека ≫ Математика ≫ Книги ≫ Глава 9. Независимость н доминирование шахматных фигур / Математика на шахматной доске // Гик Е. Я. |








Warning: Use of undefined constant expert_review_likes - assumed 'expert_review_likes' (this will throw an Error in a future version of PHP) in /var/www/www-ars1963/data/www/ck62.ru/wp-content/themes/colormag/comments.php on line 93