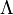какое множество называют пустым
Непустое множество
Пустым множеством в математике называется множество, не содержащее ни одного элемента.
В одних теориях множеств существование [по меньшей мере одного] пустого множества провозглашается (см. аксиому пустого множества), в других — доказывается. Во всех теориях множеств единственность пустого множества доказывается (см. аксиому объёмности).
Содержание
Обозначения пустого множества
Обычно пустое множество обозначают одним из следующих символов: 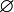
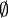
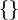
Реже пустое множество обозначают одним из следующих символов: 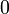
В Юникоде имеется специальный символ «пустое множество» (U+2205, ∅ ).
Символы 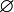
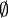
Символ 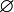
Свойства пустого множества
См. также
Ссылки
Полезное
Смотреть что такое «Непустое множество» в других словарях:
Множество — У этого термина существуют и другие значения, см. Множество (значения). Запрос «Целое» перенаправляется сюда; о типе данных в программировании см. Целое (тип данных). Множество одно из ключевых понятий математики, в частности, теории… … Википедия
ЧАСТИЧНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО — непустое множество, на к ром зафиксирован нек рый порядок. Ч. у. м. является примером модели. Примеры Ч. у. м.: 1) множество натуральных чисел с обычным порядком; 2) множество натуральных чисел, где означает, что аделит b; 3) множество всех… … Математическая энциклопедия
Направленное множество — В математике, направленным множеством называется непустое множество A с заданным на нем рефлексивным транзитивным отношением ≤ (т. е. предпорядком), обладающее дополнительным свойством: для любых двух элементов из A найдется элемент из A… … Википедия
ПРОЕКТИВНОЕ МНОЖЕСТВО — множество, к рое может быть получено из борелевских множеств повторным применением операций проектирования и перехода к дополнению. П. м. классифицируются по классам, образующим проективную иерархию. Пусть I=ww бэровское пространство… … Математическая энциклопедия
Частично упорядоченное множество — У этого термина существуют и другие значения, см. Упорядоченное множество. Подмножества
Нечёткое множество — Эту страницу предлагается объединить с Теория нечётких множеств … Википедия
Нечеткое множество — Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие… … Википедия
Пушистое множество — Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество понятие, введённое Лотфи Заде в 1965 г. в статье «Fuzzy Sets» (нечёткие множества) в журнале Information and Control [1]. Л. Заде расширил классическое канторовское понятие… … Википедия
ХНУРЭ дистанционное обучение
Новости сайта
Студентам, хто досі не має доступ до необхідних, за розкладом, навчальних дисциплін.
Шановні студенти ХНУРЕ.
Оголошення для тих, хто досі не має доступ до необхідних, за розкладом, навчальних дисциплін.
Ми не можемо підключати студентів до навчальних дисциплін на вимогу студента.
Ми підключаємо студентів тільки за заявкою викладача.
Тому, будь ласка, зверніться до викладачів тих курсів, доступу до яких у вас немає, щоб вони написали нам лист зі списком студентів, яких потрібно додати на їх дисципліну.
Внимание первокурсников!
Обратите внимание, что хотя логины для почты и системы “ХНУРЭ Дистанционное обучение” одинаковые, но пароли разные!
Новый пароль должен быть не менее 8 символов, в нем должны быть минимум 1 цифра, 1 буква в нижнем регистре и 1 буква в верхнем регистре.
Забыли или потеряли пароль?
Если Вы были зарегистрированы в нашей системе и помните свой логин (он же адрес электронной почты в домене @nure.ua), на который был зарегистрирован ваш аккаунт, воспользуйтесь системой автоматического восстановления пароля:
Восстановить пароль от dl.nure.ua
Восстановить пароль от почты можно в комнате 282 по студенческому билету.
ВНИМАНИЕ! сотрудники ЦТДО не работают со студентами напрямую, а только через ответственных за ДО. Все обращения в очную или при помощи писем на адреса сотрудников – обрабатываться не будут.
О пустом множестве
Последняя загрузка: 09.05.2021
Содержание
О пустом множестве
Точки зрения
Часто в математической литературе «легко» доказывается, что пустое множество
является подмножеством любого другого (пустого или непустого) множества.
Основой такого доказательства служат приводимые ниже определения
подмножества и пустого множества (курсив и полужирный шрифт везде мои):
1. Множество А называется подмножеством множества В, если все элементы,
2. Множество, не содержащее ни одного элемента, называется пустым
и обозначается символом Ǿ (или обычным нулём: 0).
Совершенно очевидно, что в первом определении речь идёт о двух непустых
множествах, поскольку в каждом предполагается наличие элементов, которые
и сравниваются между собой.
Теперь посмотрим, как же на основании определения подмножества, которое
ЯВНО предполагает НАЛИЧИЕ элементов как во множестве, так и в его подмножестве,
доказывается, что пустое множество, определение которого ЯВНО предполагает
ОТСУТСТВИЕ элементов в нём, является подмножеством любого (пустого или
«… Пустое множество есть подмножество любого множества. Чтобы установить это,
надо доказать, что если А есть произвольное множество, то каждый элемент Ǿ
(вот именно: КАЖДЫЙ элемент Ǿ, а в Ǿ ИХ НЕТ! – Н.М.) есть элемент подмножества А.
Поскольку Ǿ не имеет элементов, то условие выполняется автоматически».
(Какая-то казуистика! – Н.М.)
Итак, «доказали»: каждый элемент Ǿ есть элемент А! Ну и ну! Так, чего доброго,
можно доказать и противоположное: Ǿ не является подмножеством А,
поскольку Ǿ не содержит элементов! Или ещё интереснее: поскольку А не содержит
ни одного элемента из Ǿ. Каково! Попробуй, опровергни!
Тем самым всякий элемент пустого множества содержится в любом множестве М.
А значит, любое множество М содержит пустое подмножество».
Голова моя явно слаба понять это. Ведь можно сказать и так:
Тем самым ни какой элемент пустого множества не содержится ни в каком
множестве М. А значит, никакое множество М не может содержать в качестве
подмножества пустое множество».
Пожалуй, разум более приемлет второе утверждение, как более понятное; – «раз нет,
то и говорить нечего», чем утверждение – «хотя нет, но есть:» (не путать с «понятным»
определением – « хотя и нет, но можно говорить…»)
«… Заметим, между прочим, что из определения отношения А следует, что,
каково бы ни было подмножество А множества J
Таким образом, «доказательства» во всех рассмотренных случаях
аналогичны. Чувствуя неубедительность своих аргументов, некоторые авторы
приводят «косвенные» доказательства того, что Ǿ
«… Хотя такое рассуждение (смотрите выше – Н.М.) правильно, в нём имеется
нечто неудовлетворительное. Имеется и другое, косвенное доказательство,
которое может оказаться более удобным. Это может быть лишь в том случае,
не являющийся множества А. Но это невозможно, так как Ǿ не имеет элементов.
Нетрудно провести аналогичное по форме «доказательство» противоположного
факта: Ǿ не принадлежит А. Действительно. Допустим, что Ǿ не принадлежит А
ложно (т.е. Ǿ – истинно). Это может быть лишь в том случае, если
не является ложным, т.е. Ǿ не принадлежит А ».
«… Свойство 4) (см. выше – Н.М.) может показаться несколько парадоксальным,
но если вдуматься (я очень пытался, но оказался слабоват – Н,М,), оно логически
строго соответствует точному смыслу определения знака
В самом деле, соотношение Ǿ нарушалось бы только в том случае,
если бы пустое множество Ǿ содержало элемент(да нету их там вообще. – Н.М.),
который не содержался бы в А, но так как пустое множество не содержит вовсе
элементов, то этого быть не может, каково бы ни было А».
А вот аналогичное по форме, но противоположное по результатам доказательство;
соотношение Ǿ не принадлежит А нарушалось бы только в том случае, если бы
множество А содержало бы все элементы … и т.д. и т.п. ( смотрите ранее
приведённое «контрдоказательство»).
Итак, любое доказательство утверждения Ǿ
На мой взгляд дать определение подмножества так, чтобы соотношение Ǿ
являлось его следствием, НЕЛЬЗЯ! Дело в том, что пустое множество
КАЧЕСТВЕННО отличается от непустого именно тем, что оно не содержит элементов.
Т. е. их вообще нелогично сравнивать!
Да, трудно доказать ЧТО-ТО, когда в разряд ЧЕГО-ТО зачисляется НИЧТО.
А поэтому удобное и необходимое для нас соотношение Ǿ нужно просто
ПОСТУЛИРОВАТЬ. Я так думаю.
«… Если, как это уже предполагалось выше, ввести в рассмотрение так
называемое пустое множество, т. е. множество, не содержащее ни одного
Некоторые авторы (см. например [5], стр. 14) фактически так и поступают.
Не исключено, однако, что здесь имеет место отказ от доказательства соотношения
Ǿ ввиду его «очевидности»
«… Если, как это уже предполагалось выше, ввести в рассмотрение так
называемое пустое множество, т. е. множество, не содержащее ни одного
Новая редакцЫя 17.03.2013 9:26
Литература:
[1], Множества. Логика. Аксиоматические теории,
[3], Что такое математика?
[5], Элементы теории функций и функционального анализа
Интересно сравнить
В некоторых формулировках теории множеств существование
пустого множества постулируется (см. аксиому пустого множества),
в других — доказывается.
Тема: «Около «науки»
Страницы : 23, 24, 40, 41, 77, 78, 79.
§1. Множества и операции над ними
Объяснение и обоснование
В курсах алгебры и алгебры и начал математического анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.
Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество М состоит из чисел 1; 2; 3, то его обозначают так: М = <1; 2; 3>. Тот факт, что число 2 входит в это множество (является элементом данного множества М), записывается с помощью специального значка ∈ следующим образом: 2 ∈ М; а то, что число 5 не входит в это множество (не является элементом данного множества), записывается так: 5 ∉ М.
Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество.
Например: множество простых делителей числа 1 — пустое множество.
Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом ∅, множество всех натуральных чисел — буквой N, множество всех целых чисел — буквой Z, множество всех рациональных чисел — буквой Q, а множество всех действительных чисел — буквой R.
Множества бывают конечными и бесконечными в зависимости от того, какое количество элементов они содержат. Так, множества А = <7>и M = <1; 2; 3>— конечные, потому что содержат конечное число элементов, а множества N, Z, Q, R — бесконечные.
Множества задают или с помощью перечисления их элементов (это можно сделать только для конечных множеств), или с помощью описания, когда задается правило (характеристическое свойство), которое позволяет определить, принадлежит или нет данный объект рассматриваемому множеству. Например, А = <–1; 0; 1>(множество задано перечислением элементов), B — множество всех четных целых чисел (множество задано характеристическим свойством всех элементов множества). Последнее множество иногда записывают так: B = или так: B =
В общем виде запись множества с помощью характеристического свойства можно обозначить так: A =
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества.
Из приведенного определения равенства множеств следует, что в множестве одинаковые элементы не различаются. Действительно, например, <1; 2; 2>= <1; 2>, поскольку каждый элемент первого множества (1 или 2) является элементом второго множества и, наоборот, каждый элемент второго множества (1 или 2) является элементом первого. Поэтому, записывая множество, чаще всего каждый его элемент записывают только один раз.
Если каждый элемент множества A является элементом множества B, то говорят, что множество A является подмножеством множества B.
Это записывают следующим образом: A ⊂ B.
Например, <1; 2>⊂ <0; 1; 2; 3>, N ⊂ Z (поскольку любое натуральное число — целое), Z ⊂ Q (поскольку любое целое число — рациональное), Q ⊂ R (поскольку любое рациональное число — действительное).
Полагают, что всегда ∅ ⊆ A, то есть пустое множество является подмножеством любого множества.
Иногда вместо записи A ⊂ B используется также запись A ⊆ B.
Сопоставим определение равенства множеств с определением подмножества. Если множества А и В равны, то: 1) каждый элемент множества А является элементом множества В, следовательно, А — подмножество В (A ⊆ B); 2) каждый элемент множества В является элементом множества А, следовательно, В — подмножество А (B ⊆ A). Таким образом,
два множества равны тогда и только тогда, когда каждое из них является подмножеством другого.
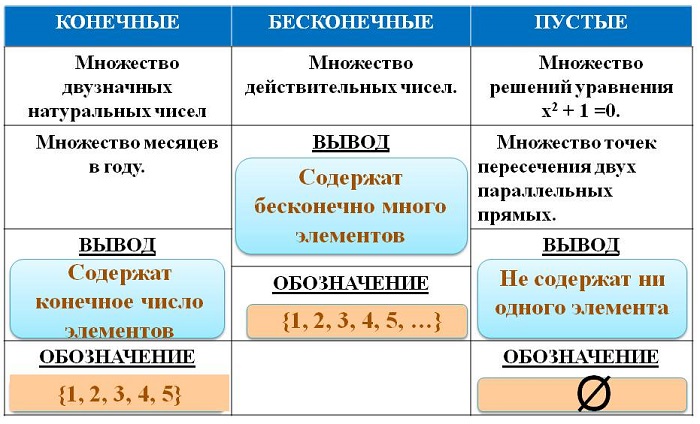
Иногда соотношения между множествами удобно иллюстрировать с помощью кругов (которые часто называют кругами Эйлера–Венна). Например, рисунок 1 иллюстрирует определение подмножества, а рисунок 2 — отношения между множествами N, Z, Q, R.
Что такое множество в математике и как оно обозначается
Множество – это количество предметов или чисел, обладающих общими свойствами.
Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит: толпа людей, стог сена, звезды в небе.
В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.
Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a1, a2 и т. д.
Границы совокупности обозначаются фигурными скобками < >.
А = <а, в, с, у>– А состоит из четырех элементов.
Записать совокупность Z согласных букв в слове «калькулятор»:
Z = <к, л, т, р>, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.
Принадлежность элементов множеству обозначается знаком – Є.
Пример: N =
Выделяют три вида множеств:
пустые (обозначаются Ø) – не имеющие элементов.
Пример: А = <а, в, с, у>и В = <а, в, с, е, к>– все элементы А являются элементами совокупности В, следовательно А ⊆ В.
Если множества состоят из одинаковых элементов, их называют равными.
Пример: А = <23, 29, 48>и В = <23, 29, 48>, тогда А = В.
В математике выделяют несколько числовых совокупностей. Рассмотрим их подробнее.
Множество натуральных чисел
Относится ли ноль к натуральным числам? Это до сих пор открытый вопрос для математиков всего мира.
Множество целых чисел
Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль:
Множество рациональных чисел
Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел:
Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное:
Следовательно, N и Z являются подмножествами Q.
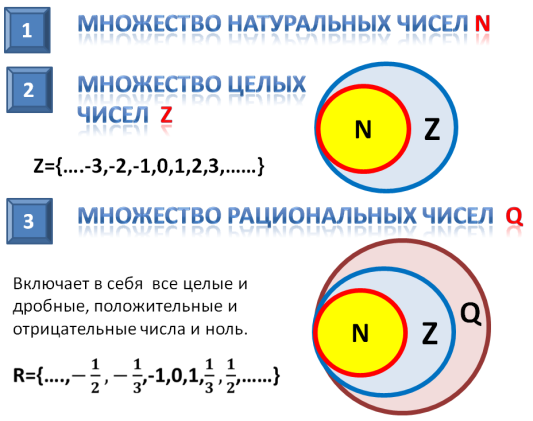
Операции над множествами
Точно так же, как и все математические объекты, множества можно складывать и вычитать, то есть совершать операции.
Если две группы образуют третью, содержащую элементы исходных совокупностей – это называется суммой (объединением) множеств и обозначается знаком ∪.
Если две группы совокупностей образуют третью, состоящую только из общих элементов заданных составляющих, это называется произведением (пересечением) множеств, обозначается значком ∩.
Если две совокупности образуют третью, включающую элементы одной из заданных групп и не содержащую элементы второй, получается разность (дополнение) совокупностей, обозначается значком /.
В случае, когда В / С = С / В, получается симметричная разность и обозначается значком Δ.
Для «чайников» или кому трудно даётся данная тема операции с совокупностями можно отобразить с помощью диаграмм Венна:
Объединение
Пересечение
Дополнение
С помощью данных диаграмм можно разобраться с законами де Моргана по поводу логической интерпретации операций над множествами.
Свойства операций над множествами
Операции над множествами обладают свойствами, аналогичными правилу свойств сложения, умножения и вычитания чисел:
Коммутативность – переместительные законы:
умножения S ∩ D = D ∩ S;
сложения S ∪ D = D ∪ S.
Ассоциативность – сочетательные законы:
умножения (S ∩ F) ∩ G = S ∩ (F ∩ G);
сложения (S ∪ F) ∪ G = S ∪ (F ∪ G).
Дистрибутивность – законы распределения:
умножения относительно вычитания S ∩ (F – G) = (S ∩ F) – (S ∩ G);
умножения относительно сложения G ∩ (S ∪ F) = (G ∩ S) ∪ (G ∩ F);
сложения относительно умножения G ∪ (S ∩ F) = (G ∪ S) ∩ (G ∪ F).
если S ⊆ Fи F ⊆ J, то S ⊆ J;
если S ⊆ F и F ⊆ S, то S = F.
Идемпотентность объединения и пересечения:
О других свойствах операций можно узнать из картинки:
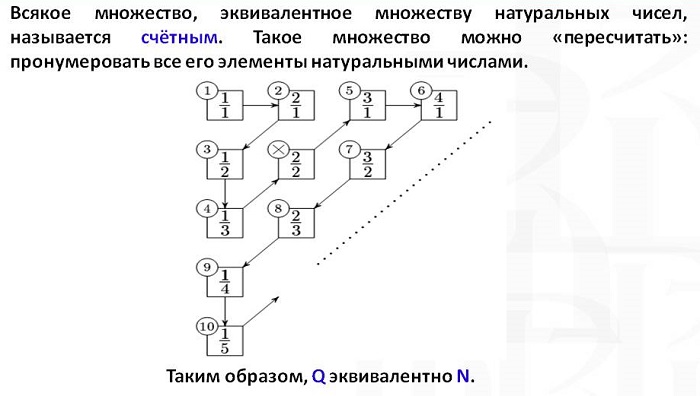
Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.
Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.