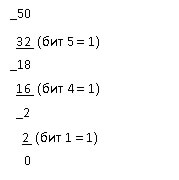какое максимальное десятичное число можно записать 1 байтом
Какое максимальное число в десятичной системе помещается в 1 байт?
Информатика. Какое максимальное число в десятичной системе счисления можно поместить в один байт?
Целые беззнаковые числа, записанные в одном байте, имеют диапазон:
Числа со знаком, записанные в дополнительном коде в один байт, имеют диапазон:
Таким образом, самое большое число какое можно записать в один байт, это будет число 255, в беззнаковом написании.
Официально пересдавать ЕГЭ летом, до начала приема в ВУЗы можно только один из обязательных предметов. Информатика и ИКТ это предмет для сдачи ЕГЭ по выбору. С такими предметами министерство образования еще не решило, нт скорее всего, в сентябре и в некоторые ВУЗы или СУЗы можно будет еще успеть на набор.
Нет, на ЕГЭ по информатике калькуляторы брать нельзя. Задания на экзамене легко считаются без использования электронных вычислительных средств, либо компьютера. Запрет калькулятора вызван также стремлением уровнять всех учеников в шансах и возможностях.
ЕГЭ по информатике 2013
Единый государственный экзамен по информатике состоится 30 мая 2013 года. Что бы сдать этот экзамен необходимо набрать минимум 40 баллов (это самое большое количеств баллов из всех предметов). В перерасчете на первичные баллы получается нужно набрать 8 первичных балов, а это восемь самых простых заданий, если же вы смогли решить более сложные задания, то вы заработаете больше баллов.
Минимальный балл прохождения ЕГЭ по Информатике 2018, дающий возможность поступить в ВУЗ составляет:
Сдавшие успешно и на очень высокую оценку в от 68 и до 100 баллов будут приняты наиболее престижными российскими ВУЗами.
Минимальный и проходной балл по Информатике 2018 года:
На сегодняшний день никаких изменений или дополнений по Информатике 2018 года не было. Хотя они еще возможно появятся, но вряд ли, поскольку времени уже совсем нет. Исходя из этого будущим студентам нужно ориентироваться на систему оценки ЕГЭ по Информатике предыдущего года.
Информация по другим предметам:
Когда мой ребенок поступал на IT, мы тоже задались этим любопытным вопросом. И задали его в приемной комиссии. Нам на этот вопрос пожали плечами, но сказали буквально следующее:
А во-вторых, информатика в школе, даже в профильных лицеях, сильно отличается от того, что потом будут преподавать в ВУЗах. То есть школьный экзамен по информатике элементарно не несет никакой полезной базы. А физика, как известно, наука всех наук. И человек, хорошо разбирающийся в физике, разберется в любой технической науке. Во всяком случае, у него для этого гораздо больше шансов.
Какое максимальное и минимально число можно записать в один байт?
Какое максимальное и минимально число можно записать в один байт.
Напишите программу, которая находит минимальное и максимальное среди четных положительных чисел, записанных в файле и выводит результат в другой файл?
Напишите программу, которая находит минимальное и максимальное среди четных положительных чисел, записанных в файле и выводит результат в другой файл.
Учтите что таких числе может вообще не быть.
Докажите, что максимальное десятичное число, которое может поместиться в одном байте, равно 255?
Докажите, что максимальное десятичное число, которое может поместиться в одном байте, равно 255.
Записать максимальное и минимальное четырехзначные натуральные числа в системе счисления следующие основания 2468?
Записать максимальное и минимальное четырехзначные натуральные числа в системе счисления следующие основания 2468.
Какое минимальное основание может иметь система счисления, если в ней записано число 712?
Какое минимальное основание может иметь система счисления, если в ней записано число 712?
Какое минимальное основание имеет система счисления если в ней записаны числа 327, 282, 1051?
Какое минимальное основание имеет система счисления если в ней записаны числа 327, 282, 1051.
Срочно помощь нужна?
Срочно помощь нужна.
Дано натуральное число N.
1. Вывести на экран минимальную цифру числа и разряд, в котором она находится ; 2.
Вывести на экран максимальную цифру числа и разряд, в котором она находится ; 3.
Вывести на экран сумму максимальной и минимальной цифры.
4. Выяснить, сколько раз в натуральном числе встречается его максимальная цифра.
5. Проверить на четность минимальную цифру числа N.
Подробнее пожалуйста, и наиболее корректней)))25 баллов?
Подробнее пожалуйста, и наиболее корректней)))25 баллов!
Какое максимальное число можно записать в двух байтах в формате с фиксированной запятой?
Что означает ноль в знаке?
Чем отличается система кодирования ASCII от UNICODE?
Задание с кратким ответом какое минимальное основание может иметь система счисления, если в ней записано число 11 и число 99?
Задание с кратким ответом какое минимальное основание может иметь система счисления, если в ней записано число 11 и число 99?
СРОЧНО?
Какое максимальное число можно записать в двоичной системе 6 цифрами?
Какое максимальное число можно записать в двоичной системе 6 цифрами?
Бит | Байт | Системы счисления
Для полноты понимания работы микроконтроллера необходимо четко знать, что такое бит и байт, а также уметь применять различные системы счисления.
Основным вычислительным ядром любого микроконтроллера является микропроцессор. Именно он выполняет обработку команд или же кода, написанного программистом.
Упрощенно работу микропроцессора можно представить следующим образом. Сначала выполняется считывание данных из определенной ячейки памяти, далее выполняется их обработка и затем возвращение результата назад в ячейку памяти. Следовательно, для того, чтобы микропроцессор мог выполнять свои функции необходимо наличие памяти. Иначе ему неоткуда будет считывать данные, а затем некуда помещать результаты вычислений.
Давайте кратко рассмотрим алгоритм работы микропроцессора (МП) на примере сложения двух цифр.
Вот такой монотонной работой занимаются микропроцессоры. Для выполнения одной команды ему необходимо выполнить четыре операции. Однако современные МП выполняют более 1 000 000 000 операций за одну секунду. Микроконтроллеры же выполняют более 1 000 000 операций, чего, как правило, предостаточно для такого крохотного устройства.
Данные, с которыми оперирует микропроцессор, представляют собой набор цифр. Поэтому нашей целью является рассмотреть, какие цифры, а точнее системы счисления “понимает” микроконтроллер.
Десятичная система счисления
Десятичная система счисления нам очень близка и понятна. Возникла она очень давно, когда у людей впервые возникал необходимость подсчета чего-либо, например количества дней или определённых событий. Поскольку в те давние времена не было каких-либо технических устройств, то люди использовали для счета пальцы рук. Загибая или разгибая пальцы можно получить десять комбинаций, что очень просто и наглядно.
Математически данная она состоит из десяти разных символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, поэтому она и называется десятичной. С помощью указанных символов легко отобразить любое число.
Основанием десятичной системы является 10. Когда при счете использованы все знаки от 0 до 9, то, чтобы продолжить дальнейший счет, необходимо вместо символа 9 поставить символ 0, т. е. обнулить предыдущее значение, а слева от нуля записать символ 1. И так можно продолжать счет до бесконечности, прибавляя слева от текущей позиции цифры последующую.
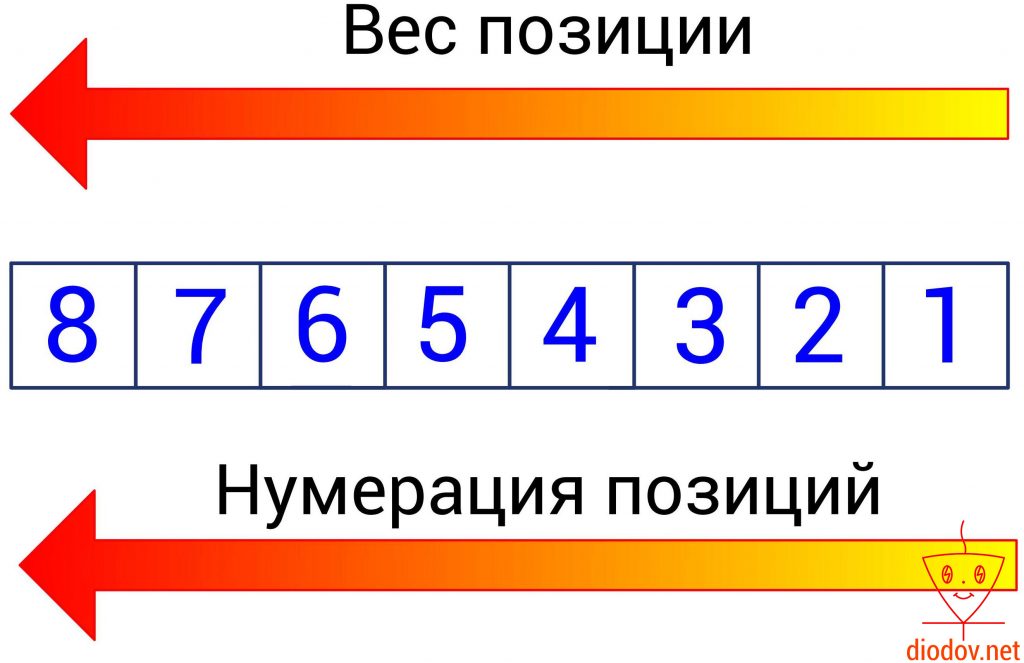
Каждая позиция цифры имеет свой вес. Наименьший вес имеет позиции, находящаяся в крайнем правом положении. По мере перемещения слева на право, вес позиции возрастает.
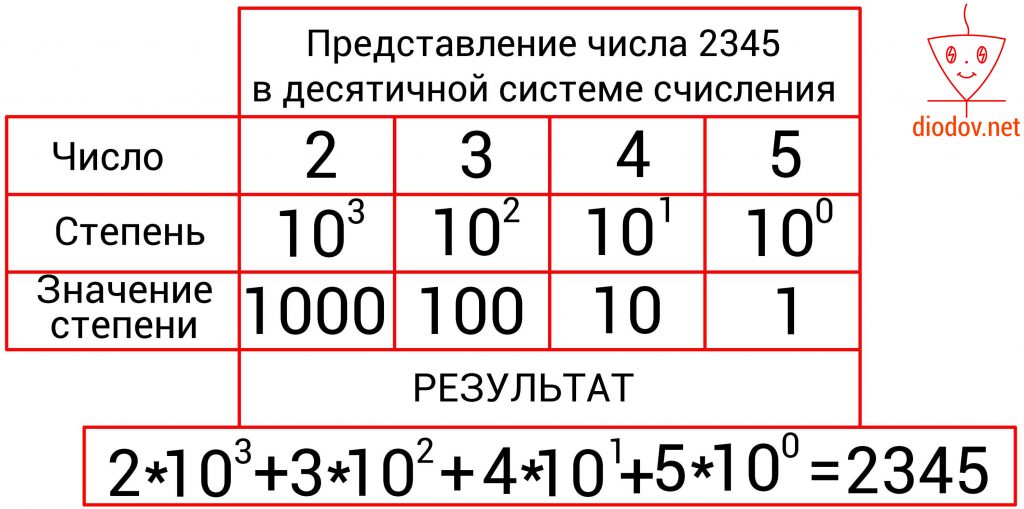
Например, число 2345 имеет 4 позиции. В крайней левой позиции отображаются единицы, в данном случае 5 единиц, а степень 10 имеет нулевое значение. Далее вес позиции увеличивается. Следующее значение, расположенное слева от предыдущего, уже содержит десятки, а 10 имеет степень 1, поэтому во второй позиции числа 2345 четыре десятка.
Двоичная система счисления
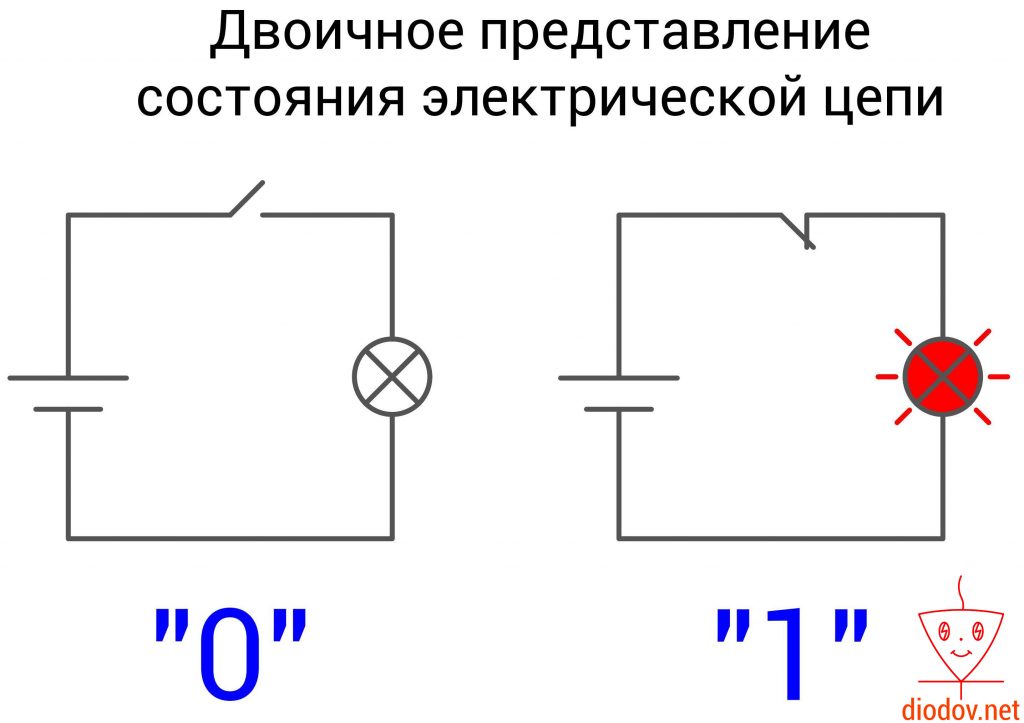
Двоичная система счисления оперирует всего лишь двумя символами 0 и 1. Она повсеместно применяется в цифровой технике, поскольку очень удачно сочетается с двумя устойчивыми состояниями электрической цепей: включено и выключено либо есть сигнал и нет сигнала. Также нулем еще обозначают сигнал низкого уровня, а единицей – высокого.
Порядок записи двоичного числа полностью соответствует десятичному. Веса позиций также возрастают справа налево. Только основанием является 2, а не 10.
Чтобы отличать двоичную систему от десятичной в цифровой технике используют индекс 2 и 10 соответственно:
110110 – десятичное.
При написании кода программы для обозначения двоичного значения перед ним ставится префикс 0b, например 0b11010101. Если записывается десятичное, то перед ним ничего не ставится.
0b11010101 – двоичное;
11010101 – десятичное.
Бит и байт
Двоичная система счисления также используется при хранении и обработке информации.
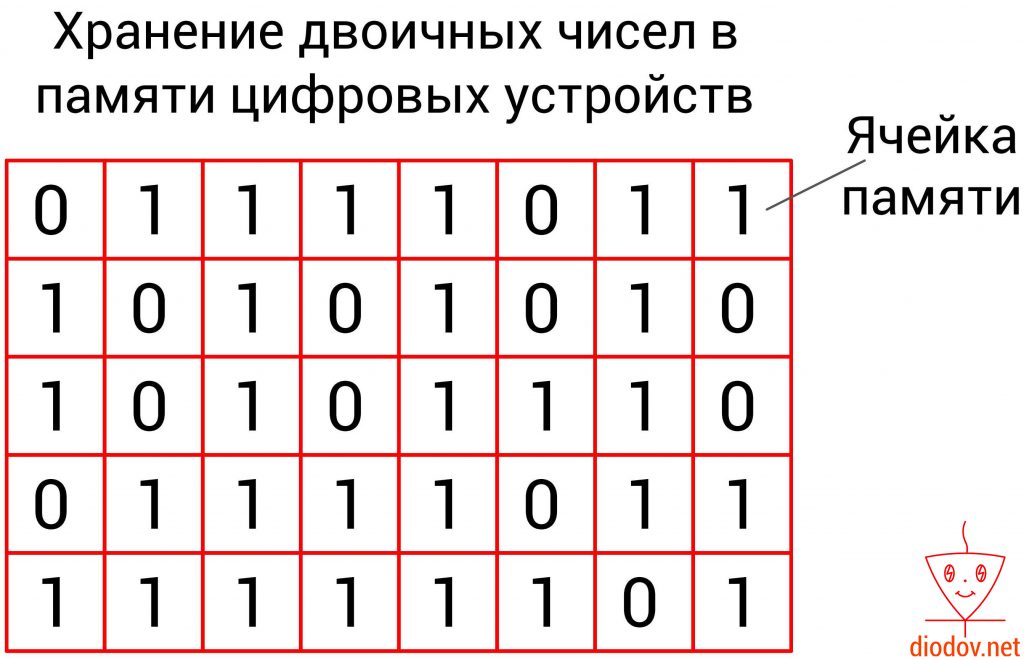
Вся информация цифровых запоминающих устройств хранится в памяти. Память представляет собой набор ячеек.
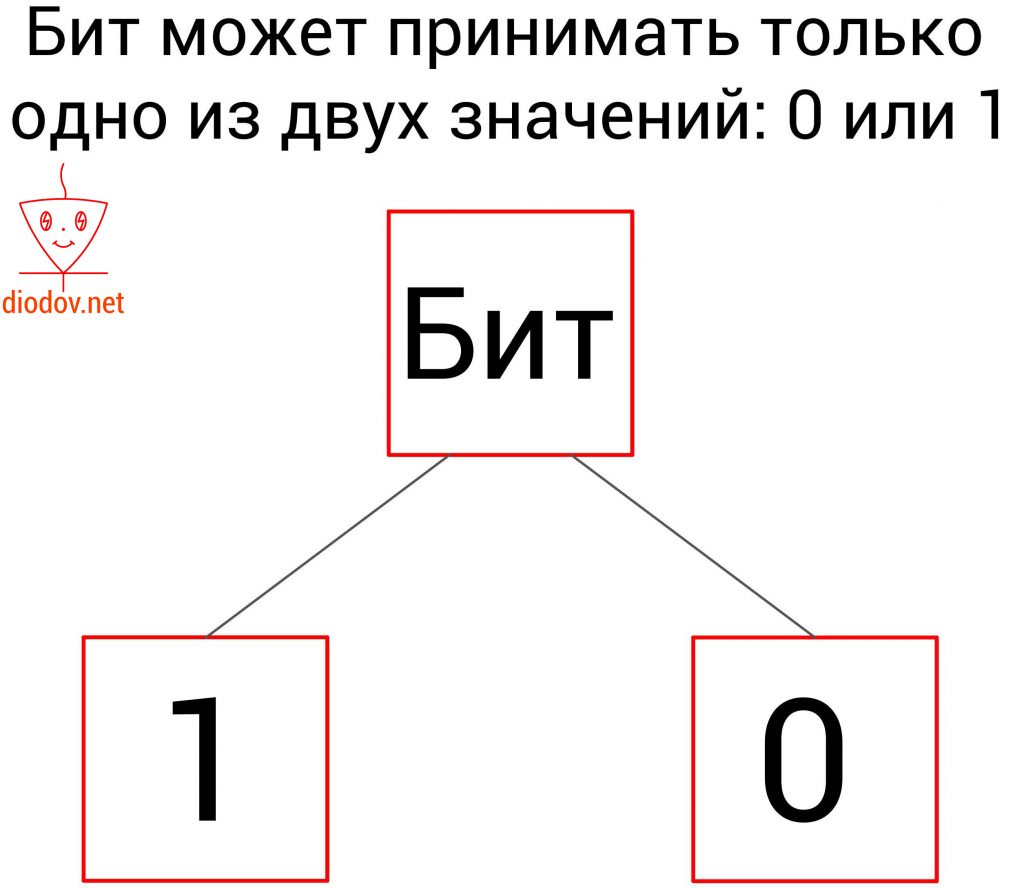
Каждая ячейка содержит один бит данных. Бит – это единица измерения объема памяти. В одном бите можно запоминать максимум два значения: 0 – это одно значение, а 1 – второе.
Bit происходит от двух английских слов Binary Digit (двоичное число).
При работе с битами регистров микроконтроллера мы будем часто обращаться к таким понятиям, как старший и младший биты. Эти понятия строго регламентированы. В двоичной системе разряд, который имеет самую правую позицию, получил название младший значащий бит (МЗБ). В англоязычной литературе его называют Least Significant Bit (LSB). Именно с него начинается нумерация битов.
Наибольший вес имеет бит, находящийся в самой левой ячейке памяти. Его принято называть старший значащий бит (СЗБ) или Most Significant Bit – MSB.
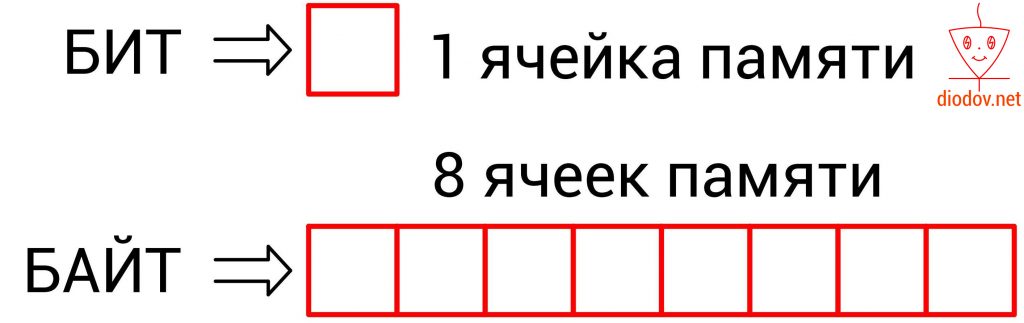
Более емкой единицей информации является байт (byte). Он равен 8 битам, т. е. восемь элементарных ячеек памяти составляют один байт.
1 байт = 8 бит
В одном бите можно хранить только два разных значения или две комбинации. А в 1 байте можно хранить 256 различных комбинаций. Ровно столько же символов содержится в таблице кодировки ASCII. Но об этом в другой раз.
На практике пользуются большими значениями объёма памяти килобайтами, мегабайтами, гигабайтами и терабайтами.
1 килобайт (кБ) = 1024 байт
1 мегабайт (МБ) = 1024 кБ
1 гигабайт (ГБ) = 1024 МБ
1 терабайт (ТБ) = 1024 ГБ
Преобразование десятичного числа в двоичное
На практике программисты часто пользуются несколькими системами счисления. Поэтому следует научиться переводить числа из десятичной системы в двоичную. Здесь можно выделить два простых способа. Рассмотрим их по порядку.
Первый способ заключается в том, что десятичное число непрерывно делится на два. При этом учитывается полностью ли оно разделилось или с остатком. Если значение делится без остатка, как например 4/2 = ровно 2 или 6/2 = ровно 3, то записывается ноль, а если с остатком, как 3/2 или 5/2, то записывается единица.
Теперь давайте переведем число 125 в двоичную форму.
125/2 = 62 остаток 1
Получаем двоичное число 11111012
Я надеюсь здесь понятно, что если 1 разделить на 2, то математически ноль никак не получится, однако такой подход позволяет объяснить данный алгоритм.
Второй способ
Второй способ имеет такую идею. С изначального числа нужно вычесть число в степени два, которое будет меньше заданного значения. Для ускорения процесса преобразования воспользуемся следующей таблицей.
Давайте преобразуем 125.
Следует обратить особое внимание на то, что нумерация битов, во-первых, выполняется справа налево, а во-вторых начинается с нуля! Это несколько непривычно, поскольку в десятичной системе счисления счет принято начинать с единицы. Однако в цифровой технике счет всегда идет с нуля! К этому следует приучить себя заранее, так как при написании программ для микроконтроллеров мы все время будем начинать счет битов с нуля. В дальнейшем вы такому счету быстро привыкнете, поскольку и в техническом описании МК строго соблюдается данное правило.
Преобразование двоичного числа в десятичное
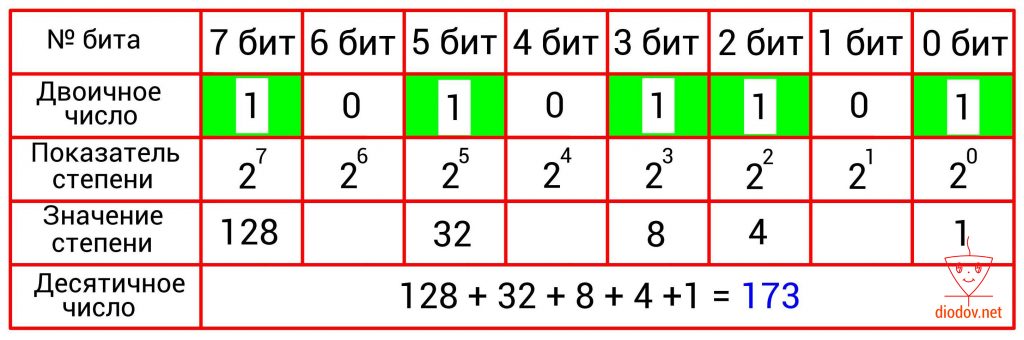
Преобразование двоичного числа в десятичное выполняется довольно просто. Для этого следует сложить десятичные веса всех двоичных разрядов, в которых имеются единицы. Биты, в которых записан ноль, пропускаются. В качестве примера возьмем такое значение: 10101101. Нулевой, второй, третий, пятый и седьмой биты имеют единицы. Получаем: 2 0 + 2 2 + 2 3 + 2 5 + 2 7 = 1 + 4 +8 + 32 + 128 = 173.
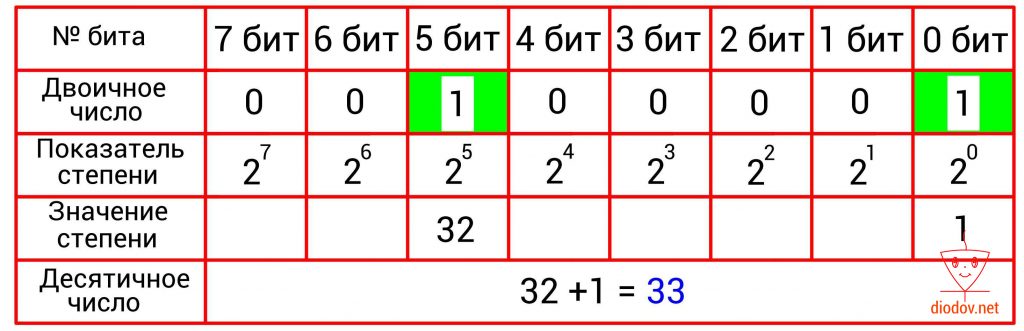
В таблицах, приведенных ниже, наглядно показано перевод чисел из двоичной в десятичную систему счисления.
Шестнадцатеричная система счисления
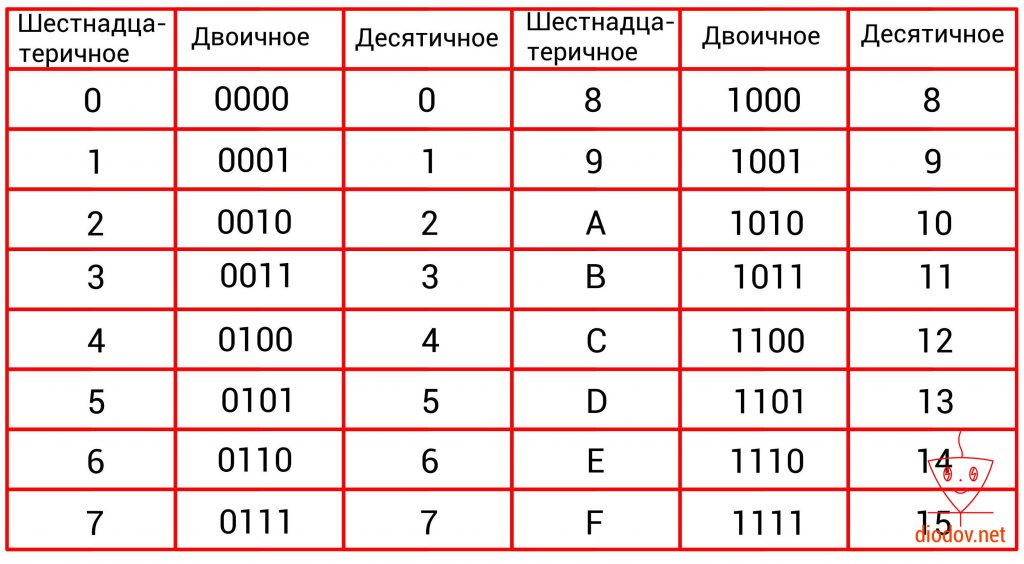
В программировании микроконтроллеров очень часто пользуются шестнадцатеричными числами. Данная система счисления имеет основание 16, соответственно и 16 различных символов. Первые десять символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 заимствованы из десятеричной системы. В качестве оставшихся шести символов применяются буквы A, B, C, D, E, F.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Высокая популярность шестнадцатеричной системы счисления поясняется тем, что при отображении одного и того же значения используется меньше разрядов по сравнению с десятичной системой и тем более с двоичной. Например, при отображении 100 используется три десятичных разряда 10010 или 7 двоичных разрядов 11001002 и только 2 шестнадцатеричных разряда 6416.
А если записать 1000000, то разница в количестве занимаемых разрядов буде еще более ощутима:
1 000 00010 = 1111 0100 0010 0100 00002 = F424016
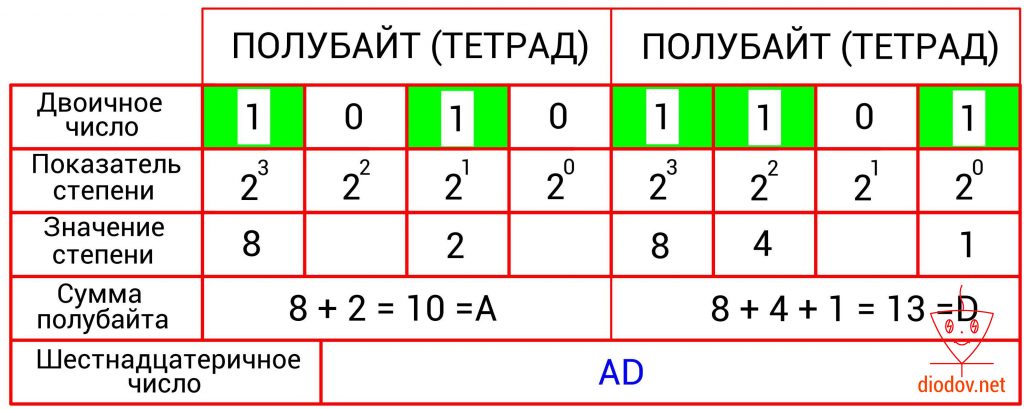
Преобразование двоичного числа в шестнадцатеричное
Еще одним положительным свойством шестнадцатеричного числа является простота получение его из двоичного. Такое преобразование выполняется следующим образом: сначала двоичное число разбивается на группы по четыре быта или на полубайты, которые еще называют тетрадами. Если количество битов не кратно четырем, то их дополняют нулями. Далее следует сложить значение всех битов в каждом полубайте. Сумма каждого полубайта даст значение отдельной цифры шестнадцатеричного числа.
Другие системы счисления
В цифровой технике также применяется восьмеричная система счисления, но она не нашла применения в микроконтроллерах.
Теоретические можно получить бесконечное значение систем счисления: троичную, пятиричную и даже сторичную, т.е. с любым основанием. Однако практической необходимости в этом пока что нет.
Наиболее простой и быстрый способ преобразования чисел с одной системы счисления в другую – это применение встроенного в операционную систему калькулятора. Найти его можно следующим образом: Пуск – Все программы – Стандартные – Калькулятор.
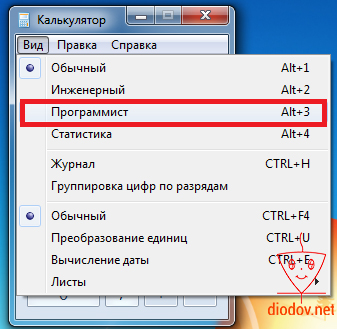
Чтобы перейти в «нужный» режим следует кликнуть по вкладке Вид и выбрать Программист или нажать комбинацию клавиш Alt+3.
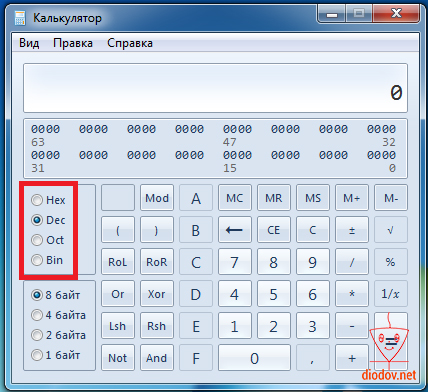
В открывшемся окне можно вводить двоичные, восьмеричные, шестнадцатеричные и десятичные числа, выбрав соответствующий режим. Кроме того можно выполнять различные математические операции между ними.
В дальнейшем, при написании кода программы мы часто будем обращаться к данному калькулятору. Кроме того, опытные программисты любят использовать шестнадцатеричные числа, а нам проще будет понять двоичный код, поэтому калькулятор в помощь)
Какое максимальное десятичное число можно записать 1 байтом
Прежде, чем рассматривать выполнение машинных программ аппаратурой ЭВМ, рассмотрим представление в памяти машины чисел, а также алфавитно-цифровых символов. Это представление потребуется нам в дальнейшем при изучении машинных программ, а также обрабатываемых ими данных.
1.1 Двоичные числа
Чтобы сделать вычислительные системы более надежными и простыми, их аппаратура строится из простейших электронных схем, которые могут находиться только в двух состояниях. Одно из них обозначается 0, а другое – 1. Такая схема предназначена для длительного или краткого хранения самой мелкой единицы информации – бита (от «BInary digiT» – двоичная цифра).
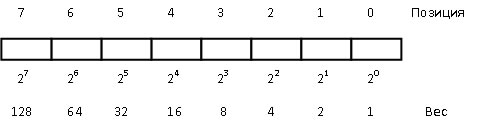
Любое число можно представить в виде цепочки битов. Такое представление числа называется двоичным числом. Цепочка из восьми битов называется байтом (рис. 1).

старший бит (бит 7) младший бит (бит 0)
Рис. 1. Пример байта
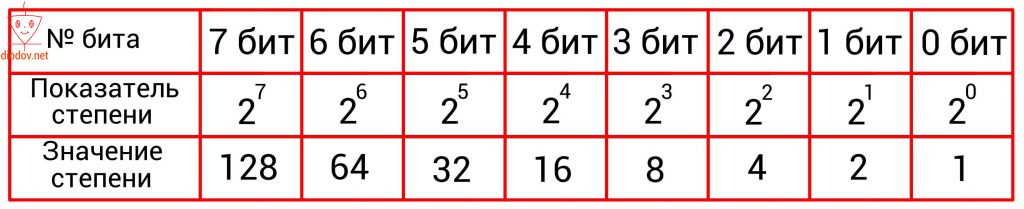
Величина двоичного числа определяется относительной позицией каждого бита и его значением. Позиционный вес младшего бита 2 о = 1(10), где 1(10) – единица в десятичной системе счисления. Следующий бит имеет вес 2 1 = 2(10). Вес любой позиции получается удвоением веса предыдущей позиции (рис. 2).
Рис. 2. Веса позиций байта
Для преобразования десятичного числа в двоичное можно использовать один из двух методов – метод деления и метод вычитания. Первый из этих методов широко используется в программах, выполняющих преобразование чисел из одной системы счисления в другую. Этот метод будет рассмотрен нами в других разделах, при описании соответствующих программ. Сейчас мы будем использовать метод вычитания, главное достоинство которого – наглядность. Согласно этому методу, для преобразования десятичного числа в двоичное надо сделать ряд вычитаний, каждое из которых даст значение одного бита.
Записывая 0 в остальные позиции битов (биты 0,2,3) получаем окончательный результат: 110010.
Для выполнения обратного преобразования следует сложить десятичные веса тех позиций, в которых стоит 1:
32 (бит 5) + 16 (бит 4) + 2 (бит 1) = 50
Байт может представлять десятичные положительные числа от 0 (00000000) до 255 (11111111). Число 255 может быть получено двумя способами: 1) суммированием весов всех битов байта; 2) по формуле 2 8 – 1, где 8 – номер первого бита, не вошедшего в состав байта.
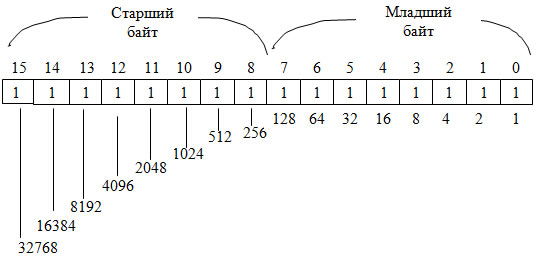
Машинным словом будем называть битовую строку длиной 16 битов. Одно слово содержит 2 байта (рис. 3). Каждый бит слова имеет свой вес. Просуммировав все веса, найдем максимальное целое число без знака, которое можно записать в одно слово, оно равно 2 16 – 1 = 65535.
Двоичное содержимое байта или слова может рассматриваться (интерпретироваться) как число без знака и как число со знаком. Число без знака занимает все 16 битов слова или 8 битов байта. Оно может быть только положительным. Просуммируем два таких числа:
Обратим внимание, что единица, появившаяся в старшем бите результата, свидетельствует лишь о возросшей величине результата, который для беззнаковых чисел может быть только неотрицательным.
Рис. 3. Веса позиций слова
все биты числа (в том числе и знаковый) инвертируются;
к полученному числу прибавляется 1.
Например, получим дополнительный код числа –65:
Для получения абсолютного значения отрицательного числа повторяют эти же самые два действия. Например:
Сумма +65 и –65 должна составить ноль:
В данном примере у нас произошли два интересных переноса: 1) в знаковый (7-й) разряд; 2) за пределы байта. Первая единица переноса обрабатывается как обычно, а вторая теряется. Оба переноса считаются правильными.
Отсюда видно, что нулевые биты в отрицательном двоичном числе фактически определяют его величину: рассмотрите весовые значения нулевых битов так, как если бы это были единичные биты, сложите эти значения и прибавьте 1.