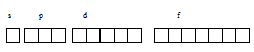
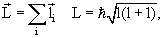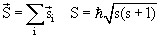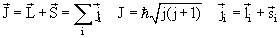какое максимальное число s p и d электронов может находиться в электронном l слое атома
Какое максимальное число s p и d электронов может находиться в электронном l слое атома
Атом
Atom
10 –13 см и электронов, образующих электронные оболочки атома. Размеры атомов определяются размерами их электронных оболочек и составляют
10 –8 см. В обычных условиях атомы электронейтральны — число электронов в атоме равно числу протонов в атомном ядре. Заряд ядра определяет порядковый номер атома в Периодической системе элементов Д.И. Менделеева. Так как масса электрона в
Замкнутая р оболочка (l=1) содержит 6 электронов
N = (2s+1)(2l+1) = (2·(1/2+1)(2·1+1) = 6.
Замкнутая d оболочка содержит 10 электронов.
Все электроны с заданным квантовым числом n образуют электронный слой, содержащий 2n 2 электронов. Слои с n = 1, 2, 3. называют в соответствии с принятой для рентгеновских спектров терминологией K, L, M, N-слоями. Максимальное число электронов в K, L, M, N-слоях приведено в таблице.
Максимальное число электронов K, L, M, N-слоях
| K-слой | L-слой | M-слой | N-слой |
| n = 1 | n = 2 | n = 3 | n = 4 |
| l = 0 | l = 0, 1 | l = 0, 1, 2 | l = 0, 1, 2, 3 |
| 2 электрона | 2 + 6 = 8 электронов | 2 + 6 + 10 = 18 электронов | 2 + 6 + 10 + 14 = 32 электрона |
Наиболее близко к ядру расположен К-слой, затем L-слой и т.д. При заданном значении n сначала заполняются состояния с l = 0, затем l = 1, l = 2 и т.д.
Последовательное заполнение электронных слоев объясняет Периодический закон элементов, открытый Д.И. Менделеевым. Периоды в Периодической системе Д.И. Менделеева соответствуют последовательному заполнению оболочек. Для элементов 1 периода происходит заполнение оболочки 1s. Для элементов 2 и 3 периодов — заполнение оболочек 2s, 2p, 3s, 3p, 3d. Однако по мере увеличения числа электронов (заряда ядра Z) такой порядок заполнения нарушается из-за конкуренции близких по энергии связи электронов. Справедливо следующее правило: чем меньше l, тем сильнее волновая функция проникает в область, экранируемую облаком внутренних электронов. В результате этого при заданном значении n энергия электронов возрастает с увеличением l (рис.).
Например, электроны 4s оказываются сильнее связаны, чем электроны 3d. В основе последовательности заполнения электронных оболочек многоэлектронных атомов лежит правило Маделунга.
Из двух оболочек ниже по энергии располагается та, для которой величина n = l оказывается наименьшей. Если для двух оболочек значения сумм n = l совпадают, то ниже по энергии лежит оболочка с меньшим значением n.
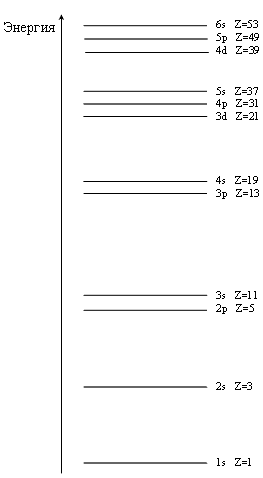 Рис. Относительное расположение электронных оболочек атомов (не в масштабе). Справа указан заряд Z ядра атома, с которого начинается заполнение указанной подоболочки. |
полного спинового момента
и полного момента количества движения
всех электронов данного атома.
Сверху слева от этого символа указывается величина 2s+1, а справа внизу значение полного момента J. Символ 4 p5/2 соответствует состоянию атома с L = 1, S = 3/2, J = 5/2.
Конкуренция спин-орбитального и электростатического взаимодействий определяет порядок сложения орбитальных и спиновых моментов. В том случае, когда электростатическое взаимодействие много больше спин-орбитального, орбитальные моменты отдельных электронов складываются в полный орбитальный момент L. Спиновые моменты отдельных электронов складываются в полный спиновый момент S.
= 
+ 
.
Такая схема связи называется L–S связью. В основном она реализуется для основных состояний лёгких ядер.
В случае, когда спин-орбитальное взаимодействие много больше электростатического, полные моменты отдельных электронов объединяются в полный момент атома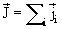 
. Такая схема связи называется j–j связью и реализуется в основном в тяжелых ядрах.
Для определения основного терма данной конфигурации используют эмпирические правила Хундта.
Ниже по энергии лежит терм, у которого мультиплетность является максимальной.
При равенстве мультиплетностей нескольких термов минимальной энергией обладает терм с максимальным значением суммарного орбитального момента конфигурации.
Если атомная подоболочка заполнена менее, чем наполовину, наименьшую энергию имеет состояние с минимальным значением J, если атомная оболочка заполнена более, чем наполовину, то наименьшую энергию имеет состояние с максимальным J.
Наряду с электронной конфигурацией, соответствующей наибольшей энергии связи всех электронов атома, при возбуждении одного или нескольких электронов образуются возбуждённые электронные конфигурации. Переходы между различными термами атома образуют спектр возбуждённых состояний атома.
Заполнение электронных орбиталей атомов элементов | Правила Клечковского
Задача 175.
Сколько значений магнитного квантового числа возможно для электронов энергетического подуровня, орбитальное квантовое число которого l = 2? l = 3?
Решение:
Атомные орбитали, которым отвечает значение орбитального квантового числа l, равное 2, называются d-орбиталями. На d-орбитали (d-подуровне) находится пять АО. Графическая схема d-подуровня имеет вид:
Ответ: 5; 7.
Задача 176.
Какое максимальное число электронов может содержать атом в электронном слое с главным квантовым числом n = 4?
Решение:
В электронном слое с главным квантовым числом n = 4 содержится четыре энергетических подуровня: s-, p-, d- и f-подуровни. Графически это можно представить в виде схемы:
Тогда максимальное число электронов в четвёртом слое равно:
Ответ: 32.
Задача 177.
Определить по правилу Клечковского последовательность заполнение электронных орбиталей, характеризующихся суммой n + l: а) 5; б) 6; в) 7.
Решение:
Согласно правилам Клечковского, АО заполняются электронами в порядке последовательного увеличения суммы n + l (первое правило Клечковского), и при одинаковых значениях этой суммы – в порядке последовательного возрастания главного квантового числа (2-е правило Клечковского).
а) По условию задачи сумма n + l = 5, причём из всех возможных комбинаций n + l, соответствующих этой сумме (n = 3, l = 2; n = 4, l = 1; n = 5, l = 0), первой будет реализоваться комбинация с наименьшим значением главного квантового числа, т.е. 3d, затем – 4p, а после 4p – 5s.
Таким образом, при сумме n + l =5 порядок заполнения орбиталей будет следующий: 3d?4p?5s..
б) При сумме n + l = 6 из всех возможных комбинаций n + l, соответствующих этой сумме (n + 4, l = 2; n = 5, l = 1; n = 6, l = 0), первой будет реализоваться комбинация с наименьшим значением главного квантового числа, т. е. 4d, затем – 5p, а после 5p – 6s.
Таким образом, при сумме n + l = 6 порядок заполнения орбиталей будет следующий: 4d?5p?6s.
Таким образом, при сумме n + l = 7 порядок заполнения орбиталей будет следующий: 4f?5d?6p?7s.
Ответ: а) 3d→4p→5s; б) 4d→5p→6s; в) 4f→5d→6p→7s.
Задача 178.
Указать порядковый номер элемента, у которого: а) заканчивается заполнение электронами орбиталей 4d; б) начинается заполнение подуровня 4р.
Решение:
а) 4d-подуровень начинает заполняться после 5s-подуровня. 5s-подуровень начинает заполняться после заполнения электронами 4p-подуровня, т.е. после заполнения оболочки криптона – элемента №36.
Согласно правилу Клечковского после криптона будет заполняться 5s-подуровень, после него – 4d-подуровень. На 5s-подуровне, состоящем из одной атомной орбитали, может находиться два электрона, а на 4d-подуровне, состоящем из пяти атомных орбиталей, может находиться десять электронов. Значит, порядковый номер элемента, с полностью заполненным 4d-подуровнем должен быть на двенадцать больше, чем у криптона (№ 36), значит, элемент № 48 (кадмий). Но, учитывая «провалы» электронов у рутения, родия и палладия с 5s-подуровня на 4d-подуровень (у рутения и родия по одному электрону, а у палладия – два), то 4d-подуровень полностью заполняется электронами у палладия (элемент № 46). Но у элемента № 47 окончательно заканчивается заполнение 4d-орбитали, и 47-й электрон занимает 5s-орбиталь. Таким образом, элемент с порядковым номером 47 считается элементом, у которого заканчивается заполнение электронами 4d-орбитали. Отсюда вывод – порядковый номер элемента 47 (серебро Ag).
б) Согласно правилу Клечковского заполнение электронами 4p-подуровня начинается после заполнения всех атомных орбиталей 3d-подуровня. Элементом, у которого заканчивается заполнение электронами 3d-подуровня является элемент № 30 (цинк). Значит, элементом, у которого начнётся заполнение электронами 4p-подуровня, будет элемент № 31 (галлий Ga).
Ответ: а) Ag; б) Ga.
Задача 179.
Какой подуровень заполняется в атомах после подуровня 5s?
Решение:
Подуровню 5s соответствует сумма n + l, равная 5 (5 + 0 = 5). Такой же суммой n +l характеризуется 4p-подуровень, но заполнению этого подуровня предшествует заполнению 5s-подуровня, так как последнему отвечает большее значение главного квантового числа (второе правило Клечковского). Следовательно, после заполнения 5s-подуровня будет заполняться подуровень с суммой n + l = 6, причём из всех возможных комбинаций n + l, соответствующих этой сумме (n + 4, l = 2; n = 5, l = 1; n = 6, l = 0), первой будет реализоваться комбинация с наименьшим значением главного квантового числа, т.е. вслед за 5s-подуровнем будет заполняться 4d-подуровень n + l = 6.
Ответ: 4d.
Задача 180.
У какого элемента начинает заполняться подуровень 4f? У какого элемента завершается заполнение этого подуровня?
Решение:
Согласно правилам Клечковского 4f-подуровень (n = 4, l = 3) с суммой n + l, равной 7, и с наименьшим значением главного квантового числа, должен заполняться после заполнения 6s-подуровня с суммой n + l, равной 6. Электронную конфигурацию последнего энергетического уровня 6s 2 имеет атом элемента № 55 (барий). Затем, у элемента № 57 (лантан), должен начать заполняться 4f-подуровень, но, на самом деле у лантана, расположенного непосредственно после бария появляется не 4f-, а 5d-электрон. Однако уже у следующего за лантаном церия (Z = 58) действительно начинается застройка 4f-подуровня, на который переходит и единственный 5d-электрон, имевшийся в атоме лантана, в соответствии с этим электронная структура атома церия выражается формулой [Kr]4f 2 6s 2 . Начиная с церия, происходит последовательное заполнение всех орбиталей 4f-подуровня. Далее, начатое заполнение 4f-подуровня у атома церия заканчивается у иттербия (Z = 70).
Ответ: Ce; Yb.
Задача 181.
Какой подуровень заполняется в атомах после заполнения подуровня 5р? После заполнения подуровня 5d?
Решение:
а) Подуровню 5p соответствует сумма n + l = 6 (5 + 1 = 6). Такой же суммой n + l характеризуются подуровни 4d и 6s. Заполнение 4d-подуровня, согласно 2-му правилу Клечковского, предшествует заполнению подуровня 5p. После заполнения электронами подуровня 5p, согласно 2-му правилу Клечковского, начнёт заполняться 6s-подуровень, которому отвечает большее значение главного квантового числа n (n = 6).
б) Подуровню 5d соответствует сумма n + l = 7 (5 + 2 = 7). Такой же суммой n + l характеризуется подуровень 4f, но заполнение этого подуровня предшествует заполнению подуровня 5d, так как последнему отвечает большее значение главного квантового числа. Следовательно, согласно 1-го правила Клечковского, будет заполняться подуровень, которому отвечает на единицу большее значение n + l (n = 6) при сумме n + l = 7. Этому условию отвечает подуровень 6p (n = 6, l = 1) при сумме n + l = 7.
Ответ: 6s; 6p.
1s → 2s → 2p → 3s → 3p → 4s → 3d → 4p → 5s → 4d → 5p → 6s →
→ (5d1) → 4f → 5d → 6p → 7s → (6d1-2) → 5f → 6d → 7p.
Так как число электронов в атоме элемента численно равно его порядковому номеру в таблице Д.И. Менделеева, то электронные формулы элементов №№ 8, 13, 18, 23, 53, 63, 83 будут иметь вид:
а) +8О 1s 2 2s 2 2p 4 ;
б) +13Al 1s 2 2s 2 2p 6 3s 2 3p 1 ;
в) +18Ar 1s 2 2s 2 2p 6 3s 2 3p 6 ;
г) +23V 1s 2 2s 2 2p 6 3s 2 3p 6 3d 3 4s 2 ;
д) +53I 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 6 4d 10 5s 2 5p 5 ;
е) +63Eu 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 6 4d 10 4f 7 5s 2 5p 6 6s 2 ;
Графические схемы заполнения валентных орбиталей атомов элементов:
Электронная структура атома может быть изображена также в виде схем размещения электронов в квантовых (энергетических) ячейках, которые являются схематическим изображением атомных орбиталей (АО). Квантовую ячейку обозначают в виде прямоугольника 
, кружочка 
или линейки 
, а электроны в этих ячейках обозначают стрелками 
. В каждой квантовой ячейке может быть не более двух электронов с противоположными спинами, например 
Мы будем применять линейки. Орбитали данного подуровня заполняются сначала по одному электрону с одинаковыми спинами, а затем по второму электрону с противоположными спинами (правило Хунда):
Строение электронных оболочек атомов элементов первых четырёх периодов: s-, p-, d-элементы
Содержание:
Тема строения атома – это место встречи химии и квантовой физики. В атоме всё подчиняется строгим законам, но в то же время атом не совсем понятен для человеческого ума. Например, количество электронов строго равно количеству протонов, но невозможно точно сказать, в каком месте атома находится электрон. Шрёдингер рассматривал электрон как облако с отрицательным зарядом. Большинство своего времени электрон в отдельном участке атома – орбитали.
Все электроны в атоме расположены на своём расстоянии от ядра – в электронной оболочке. Электрон не может приблизиться к ядру, но и отдалиться тоже не может. Дело в том, что у электрона есть свой запас энергии. Чем её меньше, тем ближе от ядра располагается электрон. Электроны с одинаковым уровнем энергии группируются в один слой – энергетический уровень.
Главное квантовое число и энергетический уровень
Квантовые числа — это своеобразный код записи положения электрона в атоме. Если сравнить атом с домом, то квантовые числа – это адрес электрона: этаж, квартира, комната.
Электроны в атоме сосредоточены на энергетических уровнях – «этажах». Их нумеруют числами 1, 2, 3, … или буквами K, L, M, N, O, P, Q. Главное квантовое число n – это и есть номер энергетического уровня.
С удалением от ядра число электронов возрастает. Чем выше энергетический уровень, тем больше электронов на нём находится. Их максимальное число для каждого уровня определяется по формуле:
На внешнем энергетическом уровне не может находиться больше 8 электронов.
В энергетических уровнях также выделяют подуровни. Их количество также соответствует главному квантовому числу. Это напоминает расположение квартир в доме: на первом этаже располагается одна квартира, на втором – две, на третьем – три и т.д.
| Номер уровня (n) и его буквенное обозначение | Количество подуровней | Максимальное количество электронов на уровне |
| 1 К | 1 (s) | 2 |
| 2 L | 2 (s, p) | 8 |
| 3 M | 3 (s, p, d) | 18 |
| 4 N | 4 (s, p, d, f) | 32 |
Орбитальное (побочное), магнитное квантовые числа и форма орбитали
Конкретное место в атоме, «комната», в которой почти постоянно находится электрон, называется орбиталью. Орбитали напоминают облака разной формы из электронов. Подуровни и форму орбиталей обозначают латинскими буквами: s, p, d, f.
Эту схему предложил Бор, она помогает разобраться в строении атома, но не отражает реальной картины. Наши представления об атоме расходятся с реальностью. И выглядит это примерно так:
На первом энергетическом уровне есть только сферическая s-орбиталь. На втором энергетическом уровне появляются три p-орбитали. Их форма напоминает гантель или восьмёрку. На третьем энергетическом уровне уже есть пять d-орбиталей, которые как бы состоят из нескольких лепестков. На четвёртом уровне возникают семь f-орбиталей.
Форму орбиталей обозначают орбитальным (побочным) квантовым числом l (эль). Оно на единицу меньше главного квантового числа, то есть l = n – 1. Тогда получается, что орбитальное число единственной s-орбитали первого энергетического уровня равно нулю. Орбиталь p имеет число 1, орбиталь d – 2, f – 3.
Но как же располагаются орбитали внутри одного подуровня? Дело в том, что движущийся электрон создаёт магнитное поле, в котором по осям x, y, z ориентируются орбитали.
Сферическая s-орбиталь не имеет ориентации в пространстве. Три p-орбитали располагаются в трёх различных проекциях, d – в пяти, f – в семи проекциях. Другими словами, сколько орбиталей одного типа, столько и проекций.
Магнитное квантовое число ml показывает, какие проекции есть у орбитали. Количество таких вариантов определяется по формуле 2l+1.
Для s-орбитали l = 0 и ml = 0, так и получается, что сфера принимает только одно положение в пространстве.
Спин электрона
Еще два квантовых числа – спиновое и проекция спина – характеризуют уникальное квантовое свойство электрона. Спин не имеет аналогов в классической механике. Можно представить, что электрон вращается вокруг своей оси в одну или другую сторону.
Квантовые числа
В атомах первого периода таблицы Менделеева есть один энергетический уровень. В нём один или два электрона движутся по s-единственной орбитали.
В атомах второго периода появляется второй уровень. Он состоит из s-и p-подуровней. Второй s-подуровень – это тоже s-орбиталь, на p-подуровне есть три орбитали, которые по-разному расположены в пространстве. Каждая p-орбиталь вмещает 1 или 2 электрона, поэтому максимально на p-подуровне их может быть 6.
В атомах третьего периода появляется d-подуровень с пятью d-орбиталями, в атомах четвёртого периода – f-подуровень с семью f-орбиталями.
Как заполняются орбитали?
Электроны заполняют орбитали в соответствии с 3 принципами (правилами).
СТРУКТУРА АТОМА
СТРОЕНИЕ МНОГОЭЛЕКТРОННЫХ АТОМОВ
Принцип Паули
В 1925 г. П. Паули постулировал принцип запрета, согласно которому:
Это означает, что электроны должны отличаться значением хотя бы одного квантового числа. Первые три квантовых числа характеризуют орбиталь, на которой находится электрон. И если два электрона имеют одинаковый их набор, то это означает, что они находятся на одной и той же орбитали. В соответствии с принципом Паули они должны отличаться значением спина. Из этого следует, что на одной орбитали могут находится только два электрона с противоположными по знаку значениями спина.
Соответствие электронов конкретной АО на энергетических диаграммах отображается в виде стрелок на условном обозначении орбитали: 
и 
. Два таких электрона, находящиеся на одной орбитали и обладающие противоположно направленными спинами, называются спаренными, в отличие от одиночного (т.е. неспаренного) электрона, занимающего какую-либо орбиталь.
Пользуясь принципом Паули, подсчитаем, какое максимальное число электронов может находиться на различных энергетических подуровнях и уровнях в атоме. При l = 0, т. е. на s-подуровне, магнитное квантовое число тоже равно нулю. Следовательно, на s-подуровне имеется всего одна орбиталь. На каждой атомной орбитали размещается не более двух электронов, спины которых противоположно направлены. Итак, максимальное число электронов на s-подуровне каждой электронной оболочки равно 2. При l = 1 (р-подуровень) возможны уже три различных значения магнитного квантового числа (-1, 0, +1). Следовательно, на р-подуровне имеется три орбитали, каждая из которых может быть занята не более чем двумя электронами. Всего на р-подуровне может разместиться 6 электронов. Подуровень d (l = 2) состоит из пяти орбиталей, соответствующих пяти разным значениям ml, здесь максимальное число электронов равно 10.
| | |
| Ns,max = 2 | Np,max = 6 | Nd,max = 10 |
Первый энергетический уровень (K-слой, n = 1) содержит только s-подуровень, второй энергетический уровень (L-слой, n = 2) состоит из s— и р-подуровней и т.д. Учитывая это, составим таблицу максимального числа электронов, размещающихся на различных энергетических уровнях (в электронных оболочках).
Существует определенная форма записи состояния электрона в атоме. Например, для основного состояния атома водорода она выглядит так:
Электронное строение атома с большим числом электронов, например атома бора, можно записать следующими способами:
Правило Хунда
Это правило определяет порядок размещения электронов в пределах одной электронной подоболочки для наиболее устойчивого состояния атома. Оно гласит:
В соответствии с этим правилом заполнение орбиталей одной подоболочки в основном состоянии атома начинается одиночными электронами с одинаковыми спинами. После того как одиночные электроны займут все орбитали в данной подоболочке, заполняются орбитали вторыми электронами с противоположными спинами.
Например, на 2р-подоболочке 3 электрона могут разместиться различным образом:
| Заселенность подоболочки равна 3 | ||
| Электронная конфигурация 2р 3 | ||
| Варианты размещения электронов | ||
 |  |  |
| Суммарный спин электронов | ||
 |  | |
Правило Хунда не запрещает другого распределения электронов в пределах электронной подоболочки. Состояния атома с меньшими, по сравнению с максимальным, значениями суммарного спина электронов будут энергетически менее выгодными и, в отличие от первого, называемого основным, будут относиться к возбужденным состояниям. В приведенном примере для атома азота представлены одно основное и два возбужденных состояния.
Принцип наименьшей энергии (правило Клечковского)
Принцип заключается в том, что:
| № периода (n) | 1 | 2 | 3 | 4 | 5 |
| Максимальное число электронов | 2 | 8 | 18 | 32 | 50 |
Реально же в Периодической системе наблюдается другая картина:
| № периода (n) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Максимальное число электронов | 2 | 8 | 8 | 18 | 18 | 32 | 32 |
Как видно из таблицы, периоды располагаются парами, исключение составляет только первый период, содержащий всего два элемента, у которых заполняется первый энергетический уровень, состоящий из одного подуровня, и нет внутренних электронов, которые могли бы повлиять на строение внешнего уровня. В остальных же случаях наблюдается следующая картина: строение третьего периода подобно строению второго (и оба содержат по 8 элементов), строение пятого периода подобно строению четвертого (и в обоих по 18 элементов),- седьмого подобно строению шестого (по 32 элемента).
Таким образом, в многоэлектронных атомах энергия электрона зависит не только от главного, но и от орбитального квантового числа. Главное квантовое число определяет здесь лишь некоторую энергетическую зону, в пределах которой точное значение энергии электрона определяется величиной l. При этом справедливо :
Для практического применения можно сформулировать так:
В тех случаях, когда сумма (n + l) одинакова для рассматриваемых электронных подоболочек, при распределении электронов используется :
Для практического применения можно сформулировать так:
Рассмотрим конкретное применение этого правила:
| n | 1 | 2 | 3 | 4 | 5 | 6 | |||||||||||||||
| l | 0 | 0 | 1 | 0 | 1 | 2 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 4 | 0 | 1 | 2 | 3 | 4 | 5 |
| n + l | 1 | 2 | 3 | 3 | 4 | 5 | 4 | 5 | 6 | 7 | 5 | 6 | 7 | 8 | 9 | 6 | 7 | 8 | 9 | 10 | 11 |
Для первых двух значений сумм (n + l), равных соответственно 1 и 2, нет альтернативных вариантов, и заполнение подуровней происходит в следующей последовательности: 1s и затем 2s. Начиная со значения суммы, равной 3, возникают два варианта: заполнять 2p-подуровень или 3s-подуровень. В соответствии с правилом Клечковского, выбираем тот подуровень, для которого n имеет меньшее значение, т.е. 2p-подуровень. Затем заполняется 3s-подуровень. Далее значение (n + l) = 4. Таких значений опять два: для 3р-подуровня и для 4s-подуровня (случай, аналогичный предыдущему). Сначала будет заполняться 3р-, а затем 4s-подуровень. 3d— подуровень остается свободным, так как сумма (n + l) для него больше, чем для 4s.
Применяя правило Клечковского, получим следующую последовательность заполнения энергетических подуровней:
Но такое заполнение происходит до определенного момента. Если рассмотреть изменение энергии подуровней с увеличением заряда ядра атома, то можно увидеть, что энергия всех подуровней снижается. Но скорость понижения энергии у разных подуровней не одинакова. Поэтому, если до кальция 3d-подуровень был по энергии выше 4s, то начиная со скандия и последующих элементов, его энергия резко снижается, о чем говорит, например, электронное строение иона Fe 2+ (ls 2 2s 2 2p 6 3s 2 3p 6 3d 6 ). Из приведенного электронного строения иона видно, что два валентных электрона железа ушли с менее энергетически выгодного 4s-пoдypoвня. Аналогичная инверсия энергий наблюдается у 5s— и 4f, а также у 6s— и 5f-подуровней.
Есть также и некоторые другие аномалии в строении внешних энергетических уровней, в основном у актиноидов.