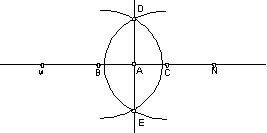Финитность алгоритма означает что

Алгоритм. Свойства алгоритма

Существует множество определений понятия «алгоритм»:

Из определений вытекают свойства алгоритма [5]:

Теперь покажем, что конкретный алгоритм обладает этими свойствами. В качестве примера, возьмем алгоритм, изображенный на рис. 1 в виде блок-схемы [6].

Рис 1 Блок-схема алгоритма проверки правильности расстановки скобок

Приведенный алгоритм проверяет правильность расстановки скобок, если скобки расставлены правильно – то каждой закрывающей скобке предшествует соответствующая открывающая, а каждой открывающей соответствует закрывающая.

Суть алгоритма заключается в подсчете глубины вложенности скобок друг в друга. Если в какой-то момент глубина получает значение меньше нуля – то скобки расставлены неправильно. Если просмотрены все символы строки, но счетчик не равен нулю – то в строке есть не закрытые скобки (расставлены неправильно). В противном случае скобки расставлены правильно.

Можно сказать, что алгоритм обладает свойством дискретности, так как весь алгоритм разбит на отдельные части (на блок-схеме это хорошо видно).

Доказать детерминированность алгоритма, достаточно сложно, например, когда алгоритм содержит части, которые выполняются параллельно, но не будем сейчас на этом останавливаться. Скажем, что в данном случае программа является детерминированной, т.к. не содержит фрагментов, зависящих от времени выполнения, т.е. сколько бы мы не тестировали алгоритм на одной и той же строке результат не изменится.

Чтобы показать результативность алгоритма, в данном случае достаточно заметить, что любой путь из начальной вершины в конечную содержит блок вывода результата. Перед блоком «конец» алгоритм содержит лишь 2 альтернативные ветви, каждая из которых выводит некоторый результат.

Алгоритм обладает свойством массовости, т.к. исходными данными для него может быть любая конечная последовательность символов. Алгоритм не обладал бы этим свойством, если бы работал лишь ограниченном наборе исходных данных, например на строках «()» и «())», но на остальных наборах не работал или работал не правильно.

Проверить свойство правильности алгоритма достаточно просто, для этого можно взять несколько примеров исходных данных, для которых результат очевиден и протестировать алгоритм на них, но доказать правильность алгоритма достаточно сложно. Доказательство правильности называется верификацией и явно выходит за рамки этой статьи.

В этой статье мы разобрались с тем, что такое алгоритм и какими основными свойствами он должен обладать. К теме алгоритмов я обязательно вернусь в будущих статьях.

Источник

Свойства алгоритма

Все алгоритмы обладают рядом свойств. Основными свойствами алгоритмов являются [4]:

1. Конечность (результативность, финитность). Свойство так определять процесс преобразования исходных данных, чтобы он через конечное число шагов для любых допустимых исходных данных приводил к искомому результату. Процедуру, обладающую всеми характеристиками алгоритма, за исключением конечности, можно назвать вычислительным методом.

2. Определенность (детерминированность). Предполагает такое составление алгоритма, которое не допускает различных толкований или искажения результата. При словесном описании алгоритмов оно дается на обычном разговорном языке, поэтому не исключена возможность неточного понимания предписания, например, человеком. Чтобы преодолеть эту трудность, для описания алгоритмов разработаны формально определенные языки программирования, в которых каждое утверждение имеет абсолютно точный смысл.

3. Ввод (массовость, наличие входных данных). Определяет возможность использования любых исходных данных из некоторого определенного множества для однотипных задач. Так, правило умножения столбиком является алгоритмом, т.к. оно используется для любых чисел (как целых, так и вещественных или дробных), но таблица умножения — не алгоритм. Это свойство подразумевает в программе наличие блока ввода, но в некоторых случаях число входных данных может быть равно нулю [4].

4. Вывод (наличие выходных данных). Алгоритм имеет одно или несколько выходных данных, имеющих определенную связь с входными данными. Здесь подразумевается наличие в программе блока вывода, иначе выполнение программы становится бессмысленным.

5. Эффективность. Алгоритм считается эффективным, если его операторы достаточно просты для того, чтобы их можно было точно выполнить в течение конечного промежутка времени.

Иногда приводят и дополнительные свойства алгоритмов, например:

Направленность. Означает наличие способа однозначного перехода от одного действия к другому.

Дискретность. Свойство, означающее, что алгоритм разбивается на последовательные команды, возможность выполнения которых человеком или машиной (исполнителем) не вызывает сомнений.

Понятность. Означает, что все команды алгоритма должны быть понятны для конкретных исполнителей.

Источник

Интуитивное понятие алгоритма

Введение

Теория алгоритмов – это раздел математики, изучающий теоретические возможности эффективных процедур вычисления и их приложения.

Теория ЭВМ, теория и практика программирования не могут без нее обойтись. Кибернетика и математическая логика рассматривают теорию алгоритмов как один из своих разделов. Например, алгоритм можно рассматривать как математическую модель программы. Однако теория алгоритмов является самостоятельной наукой и имеет собственный предмет исследования.

Само название теории говорит о том, что ее предмет – алгоритмы. Понятие алгоритма является и очень простым, и очень сложным. Его простота состоит в многочисленности алгоритмов, с которыми мы встречаемся повсюду, в их обыденности. Но эти же обстоятельства делают понятие алгоритма туманным, расплывчатым, трудно поддающимся научному определению.

Точное понятие «алгоритм» было выработано лишь в тридцатых годах XX века. До этого математики довольствовались интуитивным понятием алгоритма. Это объясняется тем, что до середины XIX века математика имела дело в основном с числами и вычислениями. Понятие алгоритма отождествлялось с понятием метода вычислений. Все многообразие вычислений комбинировалось из четко определенных операций арифметики, тригонометрии и анализа. Поэтому понятие метода вычисления считалось интуитивно ясным и не нуждалось в специальных исследованиях.

Новые более жесткие требования к строгости стимулировались в основном математикой нечисловых объектов во второй половине XIX века. Одним из решающих обстоятельств, приведших к пересмотру оснований математики, явилось создание Кантором теории множеств.

Интуитивное понятие алгоритма

Человек ежедневно встречается с множеством задач, возникающих в различных областях деятельности общества, например:

а) подготовиться к уроку по математике;

б) приготовить раствор для проявления фотопленки;

в) избавиться от лишнего веса.

Для решения задач надо знать, что дано, и что следует получить. Другими словами, задача представляет собой совокупность двух объектов: исходных данных и искомых результатов. Чтобы получить результаты, необходимо знать метод решения задачи, то есть располагать предписанием (инструкцией, правилом), в котором указано, какие действия и в каком порядке следует выполнить, чтобы решить задачу (получить искомые результаты). Предписание, определяющее порядок выполнения действий над данными с целью получения искомых результатов, называется алгоритмом.

Следует иметь в виду, что это – не определение в математическом смысле слова, но довольно подробное описание понятия алгоритма, раскрывающее его сущность. Описание может быть другим. Так, в одном из школьных учебников по информатике понятие алгоритма дается в следующей форме: «Под алгоритмом понимают понятное и точное предписание исполнителю совершить последовательность действий, направленных на решение поставленной задачи«. Математическая энциклопедия так определяет понятие алгоритма: «Алгоритм – это точное предписание, которое задает вычислительный процесс (называемый в этом случае алгоритмическим), начинающийся с произвольного данного (из некоторой совокупности возможных для данного алгоритма данных) и направленный на получение полностью определяемого этим исходным данным результата.»

Еще на самых ранних ступенях развития математики в ней стали возникать различные вычислительные процессы чисто механического характера. С их помощью искомые величины ряда задач вычислялись последовательно из исходных величин по определенным правилам. К числу таких правил относились и правила выполнения арифметических операций над числами.

Столетия эти правила были очень сложны и не удивительно поэтому, что производить вычисления с большими числами могли только люди с высшим образованием. Так, чтобы научиться арифметическому делению в средние века требовалось закончить университет. Да еще не всякий университет мог научить этой премудрости. Нужно было непременно ехать в Италию: тамошние математики добились большого искусства в делении. Если напомнить, что в те времена пользовались непозиционной (римской) системой счисления, станет ясно, почему деление миллионных чисел было доступно лишь бородатым мужам, посвятившим этому всю свою жизнь.

С введением позиционной системы счисления все изменилось. В IX веке узбекский математик Абу-Джафар Мухаммед ибн Муса ал-Хорезми («ал-Хорезми» означает «Хорезмиец») описал правила выполнения четырех арифметических действий в десятичной системе счисления. Новые правила были значительно проще и сейчас ими владеют уже школьники младших классов. Поразительная простота указанных правил стимулировала их повсеместное распространение. Эти правила были изложены Мухаммедом в книге по математике «Китаб аль-джебр валь-мукабалла» (Книга о восстановлении и противопоставлении), изданной в 825 году. В ней, кроме того, приводились многочисленные рецепты решения различных задач.

Первоначально под алгоритмами понимали только правила выполнения четырех арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи.

Для разъяснения интуитивного понятия алгоритма рассмотрим несколько примеров.

Пример 1.1. Вычисление наибольшего общего делителя двух натуральных чисел m и n.

Составим алгоритм решения этой задачи в предположении, что его исполнителем будет некоторое вычислительное устройство.

Алгоритм Евклида

1. Поместить в участок памяти с именем x число m; перейти к выполнению пункта 2.

2. Поместить в участок памяти с именем y число n; перейти к выполнению пункта 3.

З. Если выполняется условие 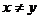, то перейти к выполнению пункта 5, иначе перейти к выполнению пункта 4.

4. Поместить в участок памяти с именем НОД значение из блока памяти x; перейти к выполнению пункта 8.

5. Если выполняется условие x > y, то перейти к выполнению пункта 6, иначе перейти к выполнению пункта 7;

8. Закончить работу.

Внимательное рассмотрение алгоритма Евклида показывает, что запись алгоритма распадается на отдельные команды. Каждая команда снабжена номером и представляет собой указание исполнителю выполнить некоторое законченное действие. Исполнение алгоритма начинается с команды, имеющей номер 1. Далее команды выполняются в соответствии с указаниями, сопровождающими каждую команду алгоритма.

Для удобства ссылок, алгоритм обычно снабжается названием. В случае, когда для алгоритма не указывается специальное название, его названием обычно считают весь текст задачи, для решения которой этот алгоритм предназначен.

Существует правило, согласно которому, при отсутствии специального указания следующей за данной командой должна выполняться команда, номер которой на единицу больше данной. Такая последовательность выполнения команд называется естественной. По указанию «кончить работу» исполнение алгоритма прекращается.

Пример 1.2. Умножение натуральных чисел столбиком.

1. Записать множимое.

2. Подписать множитель под множимым так, чтобы разряды множителя находились под соответствующими разрядами множимого.

3. Провести черту под множителем (под ней будут записываться частные суммы).

4. Взять очередную цифру множителя, начиная с единиц.

5. Если очередная цифра множителя равна нулю, пропустить ее и перейти к пункту 7.

6. Если очередная цифра не равна нулю, умножить на нее множимое и произведение как очередную частную сумму, подписать под чертой или под предыдущей частной суммой так, чтобы единицы произведения находились бы под очередной цифрой множителя.

7. Если очередная цифра не была последней, перейти к пункту 4.

8. Если очередная цифра оказалась последней, сложить частные суммы столбиком и общую сумму взять в качестве искомого произведения.

Пример 1.3. Инструкция по приготовлению проявителя. Содержимое большого пакета растворить в 300 мл. воды при температуре I8-20 ° C; затем добавить содержимое малого пакета. Объем раствора довести до 500 мл. Раствор профильтровать.

В этом примере команды не пронумерованы. Все команды записаны последовательно, в виде сплошного текста. Друг от друга команды разделены либо точкой, либо точкой с запятой. При таком оформлении алгоритма исполнитель выполняет команды в порядке их естественного следования в тексте.

Такая форма записи алгоритма часто используется во всякого рода инструкциях, правилах, рецептах и т.п. Она хороша в случае, когда алгоритм небольшой и когда для описания алгоритма отводится мало места. Недостатком такого оформления является его малая наглядность.

Свойства алгоритмов

Профессор Стенфордского университета Д.Кнут в книге «Искусство программирования для ЭВМ» отмечает, что современное значение слова «алгоритм» очень сходно со значением слов «рецепт», «процесс», «метод», «способ», «процедура», «программа», но имеет свой дополнительный смысловой оттенок. Это уточнение смысла может быть сформулировано как перечень некоторых свойств, которыми должен обладать любой алгоритм.

Перечислим те свойства, важность которых признается всеми учеными. Это: дискретность, элементарность шагов, определенность, результативность, конечность и массовость.

Рассмотренные примеры показывают, что выполнение алгоритма разбивается на последовательность законченных действий-шагов. Каждое действие должно быть закончено исполнителем прежде, чем он приступит к исполнению следующего действия. Это свойство алгоритма называется дискретностью. Таким образом, дискретность означает, что алгоритм состоит из конечного числа описаний шагов и эти шаги выполняются в дискретном времени, то есть любые два последних шага разделены при исполнении конечным, ненулевым отрезком времени. Можно считать, что шаги выполняются в моменты времени t₀, t₁,…, а между этими моментами ничего не происходит.

Произвести каждое отдельное действие исполнителю предписывает специальное указание в записи алгоритма, называемое командой.

Элементарность шагов означает, что объем работы, выполняемой на любом шаге, определяется некоторой константой, зависящей от входных данных и промежуточных значений, получаемых алгоритмом, а также от исполнителя. Понятно, что элементарность шагов для исполнителя-человека и исполнителя-ЭВМ не будет одинаковой. Для численных алгоритмов такими шагами могут быть, например, сложение, вычитание, умножение, деление, сравнение двух чисел, пересылка одного числа из некоторого места памяти в другое. Но к элементарным шагам не относится, например, сравнение двух файлов, так как время сравнения зависит от длины файлов, а длина потенциально неограниченна.

Запись алгоритма должна быть такой, чтобы на каждом шаге его выполнения было известно, какую команду надо выполнить следующей. Это свойство алгоритма называется точностью.

Алгоритм может быть выполнен только исполнителем, который понимает каждую команду алгоритма и может ее исполнить в строгом соответствии с ее назначением. Это свойство называется понятностью (для данного исполнителя).

— Да пойми же, гайками прикрепляется рельса к шпалам!

Будучи понятным, алгоритм не должен все же содержать предписаний, смысл которых может восприниматься неоднозначно. Это означает, что одно и то же предписание после исполнения должно давать один и тот же результат.

В данном случае речь фактически идет о том, что запись алгоритма должна быть настолько четкой, настолько полной и продуманной в деталях, чтобы у исполнителя никогда не могло возникать потребности в принятии каких-либо самостоятельных решений, не предусмотренных составителем алгоритма. Говоря иначе, алгоритм не должен оставлять места, для произвола исполнителя.

Отмеченное свойство называется свойством определенности, или детерминированности.

Замечание. Часто под свойством детерминированности алгоритма понимается одновременное выполнение свойств точности и понятности.

Важным свойством алгоритма является свойство результативности. Смысл этого свойства состоит в том, что при точном исполнении команд алгоритма процесс должен прекратиться за конечное число шагов, и при этом должен быть получен ответ на вопрос задачи. В качестве одного из возможных ответов может быть и установление того факта, что задача решений не имеет. В частности, если вычисляемая функция в данном шаге не определена, совокупность правил должна определять, что в этом случае следует считать результатом применения алгоритма.

Конечность (финитность) алгоритма означает, что для получения результата нужно выполнить конечное число шагов, то есть исполнитель в некоторый момент времени останавливается. Требуемое число шагов зависит отвходных данных алгоритма и не определяется константой.

Считается, что алгоритм наиболее интересен, если он, кроме того, обладает свойством массовости, т.е. пригодности для решения любой задачи из некоторого класса задач. Это свойство не следует понимать как возможность решить много задач. Свойство массовости предполагает, что заданный алгоритм позволяет решить любую задачу из определенного класса, причем этот класс может состоять и только из одной задачи.

Проиллюстрируем свойства алгоритма на примере алгоритма Евклида.

Массовость алгоритма Евклида заключается в том, что его можно применить к любой паре натуральных чисел. Результативность его состоит в том, что он определяет процесс, приводящий для любой пары натуральных чисел к получению их наибольшего делителя. Понятность алгоритма заключается в том, что исполнитель умеет выполнять действия, определяемые командами алгоритма. Детерминированность алгоритма вытекает из того, что каждая команда выполняется исполнителем однозначно. Точность алгоритма обеспечивается тем, что, во-первых, исполнителю известно, с чего начинать выполнение алгоритма (с команды номер 1), и, во-вторых, каждая команда снабжена указанием, какую команду выполнять следующей.

Рис.2.1. Непонятное предписание

Очевидно, не каждое правило, приводящее к решению задачи, является алгоритмом. Разберем с этих позиций несколько таких правил.

Пример 2.1. Проведение перпендикуляра к прямой MN в заданной точке A.

1. Отложить в обе стороны от точки A на прямой MN циркулем отрезки равной длины с концами B и C,

2. Увеличить раствор циркуля до радиуса, в полтора-два раза большего длины отрезков AB в AC.

3. Провести указанным раствором циркуля последовательно с центрами B и C дуги окружностей так, чтобы они охватили точку A и образовали две точки пересечения друг с другом D и E.

4. Взять линейку и приложить ее к точкам D и E и соединить их отрезком. При правильном построении отрезок пройдет через точку А и будет искомым перпендикуляром.

Рис. 2.2. Проведение перпендикуляра к прямой в заданной точке

Указанное правило, очевидно, рассчитано на исполнителя-человека. Применяя его, человек, разумеется, построит искомый перпендикуляр. Но, тем не менее, это правило алгоритмом не является.

Прежде всего, оно не обладает свойством детерминированности. Так, в пункте 1 требуется от исполнителя сделать выбор отрезка произвольной длины (для построения точек B и C надо провести окружность произвольного радиуса r с центром в точке A). В пункте 2 требуется сделать выбор отрезка в полтора-два раза большего длины отрезков AB и AC. В пункте 3 надо провести дуги, которые также однозначно не определяются их описанием. Человек-исполнитель, применяющий данное правило, к одним и тем же исходным данным (прямой MN и точке A) повторно, получит несовпадающие промежуточные результаты. Это противоречит требованию детерминированности алгоритма.

Попробуем переформулировать это правило, чтобы оно стало алгоритмом. Для этого следует во всех предписаниях избавить исполнителя от проблемы выбора. Вместо выбора произвольного радиуса будем указывать в каждом случае конкретный. Однако этим неопределенность команд полностью не снимается. В инструкциях 1 и 2, кроме проведения окружностей, требуется находить точки пересечения и как-то их обозначать. Разберем возникающие при этом проблемы.

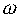
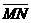
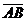
В команде 2 требуется присвоить имена точкам пересечения прямой MN и окружности . Здесь можно договориться обозначать точки, например, так, чтобы векторы и были сонаправлены.

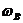
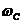
В команде 3 требуется обозначить точки пересечения окружностейи . Договоримся, например, обозначать через D ту из двух точек пересечения, которая находится левее, если смотреть из центра B в направлении центра C.

Кроме того, вместо дуг окружностей в пункте 3, мы будем проводить окружности, ибо тем самым снимается неопределенность инструкции «провести дугу, охватывающую точку».

С учетом сказанного искомый алгоритм может выглядеть следующим образом.

Пример 2.2. Алгоритм проведения перпендикуляра к прямой MN в заданной точке A ( ).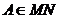

1. Провести окружность 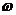радиуса 1 с центром в точке A.

2. Обозначить точки пересечения окружности 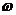с прямой MN через B и C так, чтобы .

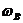
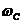
3. Последовательно провести окружности и радиуса 2 с центром соответственно в точках B и C.

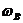
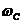
4. Обозначить точки пересечения окружностей и черезD и E так, чтобы обход многоугольника BDCE (последовательно от B через D и C к E) совершался по часовой стрелке.

Рис.2.3. Проведение перпендикуляра к прямой в заданной точке

В школьном учебнике [6] приведен алгоритм нахождения середины отрезка при помощи циркуля и линейки. В нем использован другой прием избавления от неопределенности инструкций при геометрических построениях.

Замечание. Подробное обсуждение вопросов, связанных с алгоритмами построения циркулем и линейкой, проводится в книге Абрамова С. А. «Математические построения и программирование». Всем, изучающим информатику, полезно познакомиться с этой интересной книгой.

Источник