Фильтр калмана что это

Опыт работы с фильтром Калмана на примере NMEA данных

Цель статьи не в объяснении принципов Калмановского фильтра, а в его демонстрации на примере реальных (сырых) данных. Желающие могут модифицировать исходники и поэкспериментировать с алгоритмом, я надеюсь что моя работа поможет тем, кто столкнется с подобной задачей.

Используемые данные — c GPS-приемника в формате NMEA-0183, в часности сообщения GGA и VTG.

Фильтрация необходима по причине зашумленности GPS. Причины помех в GPS данных разные. Основные:

Все это суммарно приводит к скачкам положения, смещениям курса, и прочим неприятностям. Причем в работе в первую очередь мне нужно было получить именно отфильтрованную скорость.

Дело в том что скорость, измеряемая оборудованием и передаваемая в сообщении VTG давала неправдоподобные показания (скачки и т. д.), которые крайне затрудняли задачи управления.
Поэтому было решено построить модель фильтр в Octave, и получив скорость как производную от GPS данных, представленных сообщением GGA, сравнить с оригинальными данными скорости из сообщения VTG.

Для удобства сравнения данные требуется вывести на один график.

С фильтрацией данных и их производных прекрасно справляется фильтр Калмана.

Применение фильтра для задач автопилота и курсовертикали является «классикой».

Поскольку я не специалист по теоретическим выкладкам — алгоритм работы фильтра здесь рассмотрен не будет. На эту тему есть обширные (и не очень) обзоры для всех уровней подготовки: от инженера-чайника до математика-гения с мехмата. Для читателей, незнакомых со всеми этими Predict, Update, и Invariant несколько ссылок:

Первый этап работы состоял в написании фильтра в Octave (open-source близнец Matlab для Linux). Для начала матрица управления F мат. модели была выбрана простейшей (движение без ускорения):

Впоследствии ее можно модифицировать, наращивая потенциал фильтрации.
Второй этап — перенос фильтра в вычислитель (PAC контроллер) на C++.

Первый этап работы — применение фильтра в Octave описан в этой статье.

Второй этап с С++ кодом, логированием отфильтрованных данных, передачей их в Octave и сравнением модели и реализации — возможная тема для следующей.

Описание стандартом VTG сообщения:

Два знака «—» в шапке — произвольные символы, зависящие от аппаратуры. Фильтровать будем Latitude и Longitude.

Математическая часть фильтра Калмана.

Обозначения:
Fk — матрица эволюции процесса/перехода/транзита, state-transition model.
Hk — матрица измерений/наблюдений, observation model.
Qk — матрица ковариации шума процесса, covariance of the process noise;.
Rk — матрица ковариации шума измерений, covariance of the observation noise.
K — усиление Калмана.
Xp — прогнозируемая (априорная) оценка состояния на основании прошлого состояния.
Xk — обновленная оценка состояния.
X(k-1) — обновленная оценка состояния предъидущего шага.
Pp — прогнозируемая оценка ковариационной матрицы, предсказание ошибки.
P — обновленное предсказание ошибки.
P(k-1) — ошибка (обновленная) предъидущего шага.
z- наблюдение (измерение) в текущий момент времени.

Предсказание:
Xp = Fk X(k-1); Предсказание состояния системы.
Pp = Fk P(k-1) * F’k + Q; Прогнозируемое предсказание ошибки.

Корректировка:
K = Pp H’ inv(H Pp H’ + R); Вычисление усиления Калмана.
Xk = Xp + K(z — HXp); Обновление оценки с учетом измерения z.
P = Pp — KHPp; Обновление предсказания ошибки.

Функции KalmanX и KalmanY идентичны и отличаются только названием.

Движения по X и Y фильтруются независимо, на вход фильтр принимает очередное значение, матрицы Q, R, F и признак reset (поскольку данные фильтруются несколько раз с разными Q и R, для подбора оптимальных значений).

Основной скрипт (habrGGA.m) читает дамп данных из текстового файла, вызывает функцию фильтрации, описанную выше и строит графики сырых и отфильтрованных значений.

Данные поочередно фильтруются с тремя матрицами Q, при этом матрица R остается неизменной. (Можно так же оставить неизменной Q, и менять R). Сравнивая графики, подбираем оптимальные значения коэффициентов для матриц.

На первом графике выводятся отфильтрованные координаты, или траекторию:

Мы видим оригинальные (не фильтрованные) данные, и данные с тремя разными Q. R во всех трех случаях = 0,2.

Вот увеличенный первый, наиболее зашумленный участок:

Второй и третий графики — это отдельно проекции трека на X и Y координаты (Latitude и Longitude) в верхней части, и скорости в нижней:

Увеличенные графики скорости:

Оригинальная скорость (из VTG) представлена пунктирной красной линией, фильтрованные значения хорошо сглаживают скачки.

Читатели могут поэкспериментировать с другими значениями Q и R, изменив следующую часть кода (habrGGA.m):

Для моих целей среднее значение Q (0.05) сейчас выглядит наиболее предпочтительным на данном наборе NMEA. Более точный, и возможно динамически изменяемый подбор коэффициентов будет реализован при отладке на швартовных испытаниях.

Приложенные файлы.
habrGGA.m — основной скрипт (чтение данных, вызов функции фильтрации, вывод графиков)
KalmanX.m — фильтр Калмана (Latitude)
KalmanY.m — фильтр Калмана (Longitude)

Источник

Фильтр Калмана — это легко

Много людей, в первый раз сталкивающихся в работе с датчиками, склонны считать, что получаемые показания — это точные значения. Некоторые вспоминают, что в показаниях всегда есть погрешности и ошибки. Чтобы ошибки в измерениях не приводили к ошибкам в функционировании системы в целом, данные датчиков необходимо обрабатывать. На ум сразу приходит словосочетание “фильтр Калмана”. Но слава этого “страшного” алгоритма, малопонятные формулы и разнообразие используемых обозначений отпугивают разработчиков. Постараемся разобраться с ним на практическом примере.

Об алгоритме

Что же нам потребуется для работы фильтра Калмана?

Обычно используются следующие обозначения:

— вектор состояния;
— мера неопределенности вектора состояния. Представляет из себя ковариационную матрицу (об этом позже — это будет, наверное, самая сложная часть).

Содержимое вектора состояния зависит от фантазии разработчика и решаемой задачи. Например, мы можем отслеживать координаты объекта, а также его скорость и ускорение. В этом случае получается вектор из трёх переменных: <позиция, скорость, ускорение> (для одномерного случая; для 3D мира будет по одному такому набору для каждой оси, то есть, 9 значений в векторе)

Математическая модель системы / процесса

Мы имеем дело с динамической системой, т.е. состояние системы меняется со временем. Имея модель системы, фильтр Калмана может предугадывать, каким будет состояние системы в следующий момент времени. Именно это позволяет фильтру так эффективно устранять шум и оценивать параметры, которые не наблюдаются (не измеряются) напрямую.

Фильтр Калмана накладывает ограничения на используемые модели: это должны быть дискретные модели в пространстве состояний. А ещё они должны быть линейными.

Дискретность означает для нас то, что модель работает “шагами”. На каждом шаге мы вычисляем новое состояние системы по вектору состояния с предыдущего шага. Обычно, модели такого рода задаются системой разностных уравнений.

По поводу линейности: каждое уравнение системы является линейным уравнением, задающим новое значение переменной состояния. Т.е. никаких косинусов, синусов, возведений в степень и даже сложений с константой.

Давайте разберём это уравнение подробно. В первую очередь, нас интересует первое слагаемое ( ) — это как раз модель эволюции процесса. А матрица (также встречаются обозначения , ) — называется матрицей процесса (state transition matrix). Она задаёт систему линейных уравнений, описывающих, как получается новое состояние системы из предыдущего.

Например, для равноускоренного движения матрица будет выглядеть так:

Первая строка матрицы — хорошо знакомое уравнение . Аналогично, вторая строка матрицы описывает изменение скорости. Третья строка описывает изменение ускорения.

В некоторых случаях, мы напрямую управляем процессом (например, управляем квадракоптером с помощью пульта Д/У) и нам достоверно известны задаваемые параметры (заданная на пульте скорость полёта). Второе слагаемое — это модель управления. Матрица называется матрицей управления, а вектор — вектор управляющих воздействий. В случаях когда мы только наблюдаем за процессом, это слагаемое отсутствует.

Последнее слагаемое — — это вектор ошибки модели. Модель равноускоренного движения абсолютно точно описывает положение объекта. Однако в реальном мире есть множество случайных факторов — дороги неровные, дует ветер, и т.п. Иногда, процесс сложен и приходится использовать упрощённую модель, которая не учитывает все аспекты. Именно так возникает ошибка модели.
То, что мы записываем это слагаемое, не означает, что мы знаем ошибку на каждом шаге или описываем её аналитически. Однако фильтр Калмана делает важное предположение — ошибка имеет нормальное распределение с нулевым математическим ожиданием и ковариационной матрицей . Эта матрица очень важна для стабильной работы фильтра и мы её рассмотрим позже.

Модель наблюдения

— это вектор измерения/наблюдения.Это значения, получаемые с датчиков системы.

Первое слагаемое — модель, связывающая вектор состояния с соответствующими ему показаниями датчиков. (Такой выбор модели может показаться странным, ведь наша задача — получить из , а эта модель получает из . Но это действительно так. В частности, это необходимо потому, что некоторые переменные состояния из могут отсутствовать в ).

Второе слагаемое — это вектор ошибок измерения. Как и в случае с предыдущими ошибками, предполагается, что она имеет нормальное распределение с нулевым математическим ожиданием. — ковариационная матрица, соответствующая вектору .

Вернёмся к нашему примеру. Пусть у нас на роботе установлен один единственный датчик — GPS приёмник (“измеряет” положение). В этом случае матрица будет выглядеть следующим образом:

Строки матрицы соответствуют переменным в векторе состояния, столбцы — элементам вектора измерений. В первой строке матрицы находится значение “1” так как единица измерения положения в векторе состояния совпадает с единицей измерения значения в векторе измерений. Остальные строки содержат “0” потому что переменные состояния соответствующие этим строкам не измеряются датчиком.

Количество датчиков ничем (кроме здравого смысла) не ограничено.
Например, добавим спидометр:

Второй столбец матрицы соответствует нашему новому датчику.

Несколько датчиков могут измерять один и тот же параметр. Добавим ещё один датчик скорости:

Ковариационные матрицы и где они обитают

Для настройки фильтра нам потребуется заполнить несколько ковариационных матриц:
, и .

Для нормально распределенной случайной величины её математическое ожидание и дисперсия полностью определяют её распределение. Дисперсия — это мера разброса случайной величины. Чем больше дисперсия — тем сильнее может отклоняться случайная величина от её математического ожидания. Ковариационная матрица — это многомерный аналог дисперсии, для случая, когда у нас не одна случайная величина, а случайный вектор.

В одной статье сложно уместить всю теорию вероятностей, поэтому ограничимся сугубо практическими свойствами ковариационных матриц. Это симметричные квадратные матрицы, на главной диагонали которой располагаются дисперсии элементов вектора. Остальные элементы матрицы — ковариации между компонентами вектора. Ковариация показывает, насколько переменные зависят друг от друга.

Проиллюстрируем влияние мат. ожидания, дисперсии и ковариации.

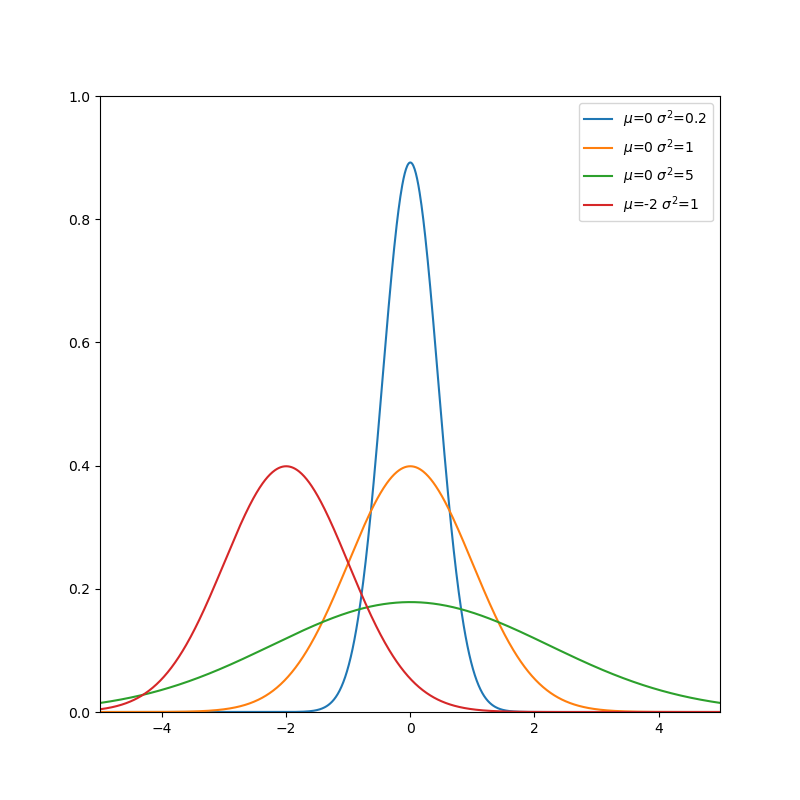
Начнём с одномерного случая. Функция плотности вероятности нормального распределения — знаменитая колоколообразная кривая. Горизонтальная ось — значение случайной величины, а вертикальная ось — сравнительная вероятность того что случайная величина примет это значение:

Чем меньше дисперсия — тем меньше ширина колокола.

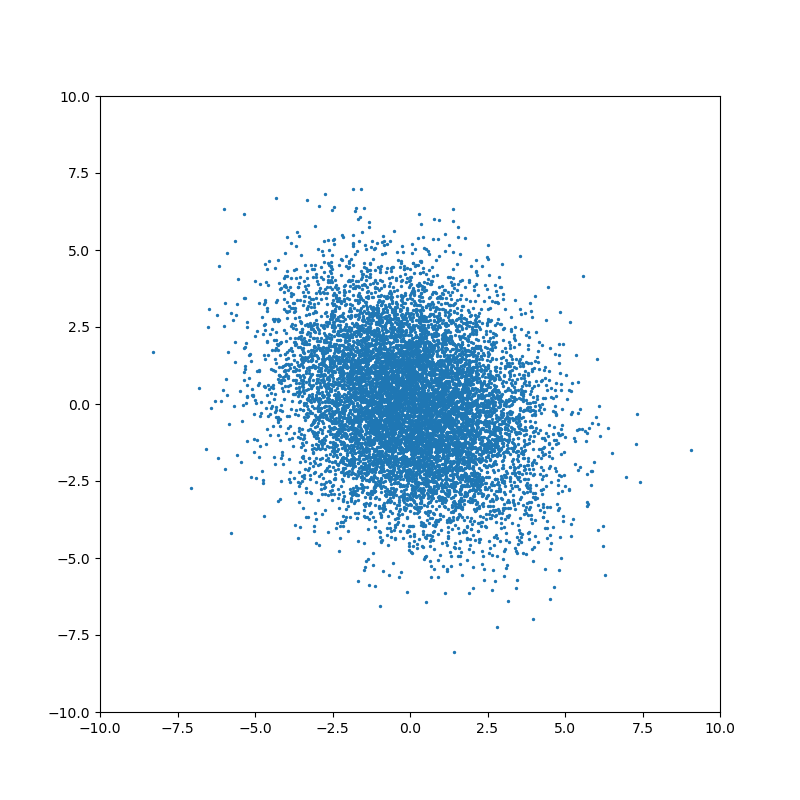
Понятие ковариации возникает для совместного распределения нескольких случайных величин. Когда случайные величины независимы, то ковариация равна нулю:

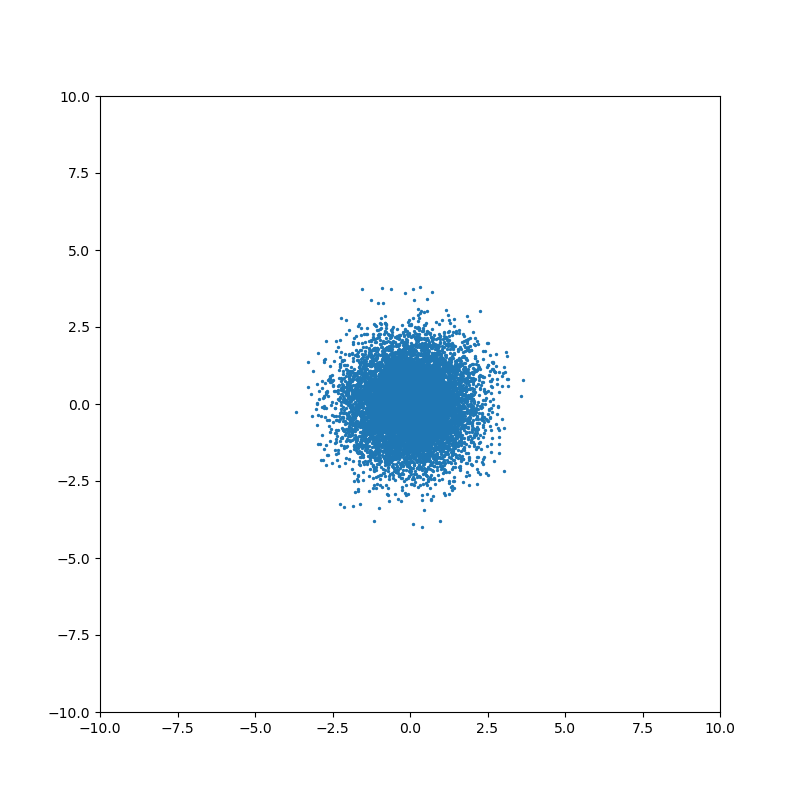
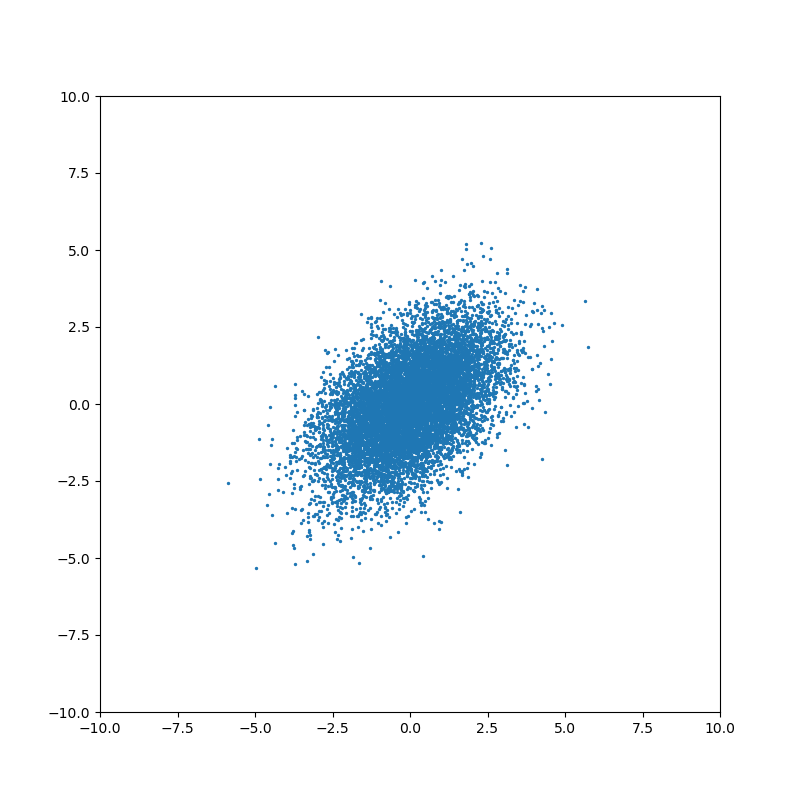
Ненулевое значение ковариации означает, что существует связь между значениями случайных величин:

На каждом шаге фильтр Калмана строит предположение о состоянии системы, исходя из предыдущей оценки состояния и данных измерений. Если неопределенности вектора состояния выше, чем ошибка измерения, то фильтр будет выбирать значения ближе к данным измерений. Если ошибка измерения больше оценки неопределенности состояния, то фильтр будет больше “доверять” данным моделирования. Именно поэтому важно правильно подобрать значения ковариационных матриц — основного инструмента настройки фильтра.

Рассмотрим каждую матрицу подробнее:

— ковариационная матрица состояния

Квадратная матрица, порядок матрицы равен размеру вектора состояния

Как уже было сказано выше, эта матрица определяет “уверенность” фильтра в оценке переменных состояния. Алгоритм самостоятельно обновляет эту матрицу в процессе работы. Однако нам нужно установить начальное состояние, вместе с исходным предположением о векторе состояния.

Во многих случаях нам неизвестны значения ковариации между переменными для изначального состояния (элементы матрицы, расположенные вне главной диагонали). Поэтому можно проигнорировать их, установив равными 0. Фильтр самостоятельно обновит значения в процессе работы. Если же значения ковариации известны, то, конечно же, стоит использовать их.

Дисперсию же проигнорировать не выйдет. Необходимо установить значения дисперсии в зависимости от нашей уверенности в исходном векторе состояния. Для этого можно воспользоваться правилом трёх сигм: значение случайной величины попадает в диапазон с вероятностью 99.7%.

— ковариационная матрица шума измерений

Квадратная матрица, порядок матрицы равен размеру вектора наблюдения (количеству измеряемых параметров).

Во многих случаях можно считать, что измерения не коррелируют друг с другом. В этом случае матрица будет являться диагональной матрицей, где все элементы вне главной диагонали равны нулю. Достаточно будет установить значения дисперсии для каждого измеряемого параметра. Иногда эти данные можно найти в документации к используемым датчика. Однако, если справочной информации нет, то можно оценить дисперсию, измеряя датчиком заранее известное эталонное значение, или воспользоваться правилом трёх сигм.

— ковариационная матрица ошибки модели

Квадратная матрица, порядок матрицы равен размеру вектора состояния.

С этой матрицей обычно возникает наибольшее количество вопросов. Что означает ошибка модели? Каков смысл этой матрицы и за что она отвечает? Как заполнять эту матрицу? Рассмотрим всё по порядку.

Каждый раз, когда фильтр предсказывает состояние системы, используя модель процесса, он увеличивает неуверенность в оценке вектора состояния. Для одномерного случая формула выглядит приблизительно следующим образом:

Если установить очень маленькое значение , то этап предсказания будет слабо увеличивать неопределенность оценки. Это означает, что мы считаем, что наша модель точно описывает процесс.

Если же установить большое значение , то этап предсказания будет сильно увеличивать неопределенность оценки. Таким образом, мы показываем что модель может содержать неточности или неучтенные факторы.

Для многомерного случая формула выглядит несколько сложнее, но смысл схожий. Однако, есть важное отличие: эта матрица указывает, на какие переменные состояния будут в первую очередь влиять ошибки модели и неучтённые факторы.

Допустим, мы отслеживаем перемещение робота, используя модель равноускоренного движения, и вектор состояния содержит следующие переменные: положение x, скорость v и ускорение a. Однако, наша модель не учитывает, что на дороге встречаются неровности.

Когда робот проходит неровность, показания датчиков и предсказание модели начнут расходиться. Структура матрицы будет определять, как фильтр отреагирует на это расхождение.

Мы можем выдвинуть различные предположения относительно природы шума. Для нашего примера с равноускоренным движением логично было бы предположить, что неучтённые факторы (неровность дороги) в первую очередь влияют на ускорение. Этот подход применим ко многим структурам модели, где в векторе состояния присутствует переменная и несколько её производных по времени (например, положение и производные: скорость и ускорение). Матрица выбирается таким образом, чтобы наибольшее значение соответствовало самому высокому порядку производной.

Модель непрерывного белого шума

Мы предполагаем, что ускорение постоянно на каждом шаге. Но из-за неровностей дороги ускорение, на самом деле, постоянно изменяется. Мы можем предположить, что изменение ускорения происходит под воздействием непрерывного белого шума с нулевым математическим ожиданием (т.е. усреднив все небольшие изменения ускорения за время движения робота мы получаем 0)

В этой модели матрица Q рассчитывается следующим образом

Мы формируем матрицу Qc в соответствии со структурой вектора состояния. Наивысшему порядку производной соответствует правый нижний элемент матрицы. В случае, если в векторе состояния несколько таких переменных, то каждая из них учитывается в матрице.
Для нашей модели равноускоренного движения матрица будет выглядеть так:

— спектральная плотность мощности белого шума

Подставляем матрицу процесса, соответствующую нашей модели:

После перемножения и интегрирования получаем:

Модель “кусочного” белого шума

— мощность шума
— наивысший порядок производной, используемой в модели (т.е. ускорение для вышеописанной модели)

В этой модели матрица определяется следующим образом:

Из матрицы процесса F

берём столбец с наивысшим порядком производной

и подставляем в формулу. В итоге получаем:

Обе модели являются приближениями того, что происходит на самом деле в реальности. На практике, приходится экспериментировать и выяснять, какая модель подходит лучше в каждом отдельном случае. Плюсом второй модели является то, что мы оперируем дисперсией шума, с которой уже хорошо умеем работать.

В некоторых случаях прибегают к грубому упрощению: устанавливают все элементы матрицы равными нулю, за исключением элементов, соответствующих максимальным порядкам производных переменных состояния.

Действительно, если рассчитать по одному из приведённых выше методов, при достаточно малых значениях , значения элементов матрицы оказываются очень близкими к нулю.

Т.е. для нашей модели равноускоренного движения можно взять матрицу следующего вида:

И хотя такой подход не совсем корректен, его можно использовать в качестве первого приближения или для экспериментов. Без сомнения, не стоит выбирать матрицу таким образом для любых важных задач без весомых причин.

Во всех примерах выше используется вектор состояния и может показаться, что во всех случаях дисперсия, соответствующая наивысшему порядок производной, находится в правом нижнем углу матрицы. Это не так.

Рассмотрим вектор состояния

Матрица будет представлять собой блочную матрицу, где отдельные блоки 3х3 элементов будут соответствовать группам и . Остальные элементы матрицы будут равны нулю.

Дисперсия, соответствующая наивысшим порядкам производных и , будет находиться на 3-ей и 5-ой позициях на главной диагонали матрицы.

Однако, на практике нет никакого смысла перемешивать порядок переменных состояния таким образом, чтобы порядки производных шли не по очереди — это просто неудобно.

Пример кода

Нет смысла изобретать велосипед и писать свою собственную реализацию фильтра Калмана, когда существует множество готовых библиотек. Я выбрал язык python и библиотеку filterpy для примера.

Чтобы не загромождать пример, возьмем одномерный случай. Одномерный робот оборудован одномерным GPS, который определяет положение с некоторой погрешностью.

Моделирование данных датчиков

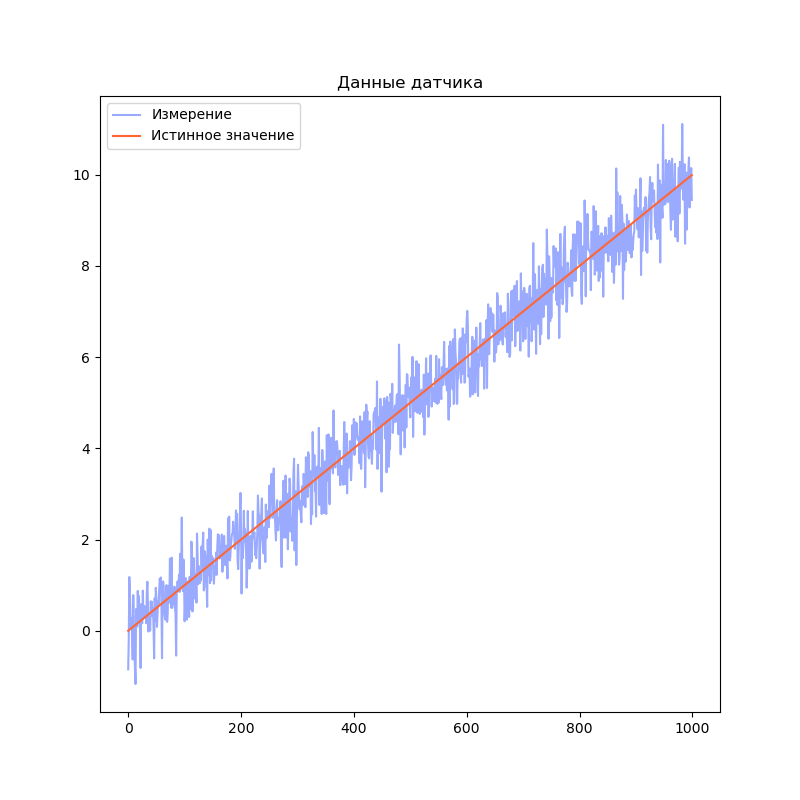
Начнём с равномерного движения:

Визуализируем результаты моделирования:

Реализация фильтра

У нас единственный датчик, который напрямую измеряет положение. Поэтому модель наблюдения получается очень простой:

Мы предполагаем, что наш робот находится в точке 0 и имеет нулевые скорость и ускорение в начальный момент времени:

Однако, мы не уверены, что это именно так. Поэтому установим матрицу ковариации для начального состояния с большими значениями на главной диагонали:

Я воспользовался функцией библиотеки filterpy для расчёта ковариационной матрицы ошибки модели: filterpy.common.Q_discrete_white_noise. Эта функция использует модель непрерывного белого шума.

Бонус — сравнение различных порядков моделей

Сравним поведение фильтра с моделями разного порядка. Для начала, смоделируем более сложный сценарий поведения робота. Пусть робот находится в покое первые 20% времени, затем движется равномерно, а затем начинает двигаться равноускоренно:

В предыдущем примере мы использовали модель, содержащую переменную (положение) и две производных её по времени (скорость и ускорение). Посмотрим, что будет, если избавиться от одной или обеих производных:

Сравним результаты: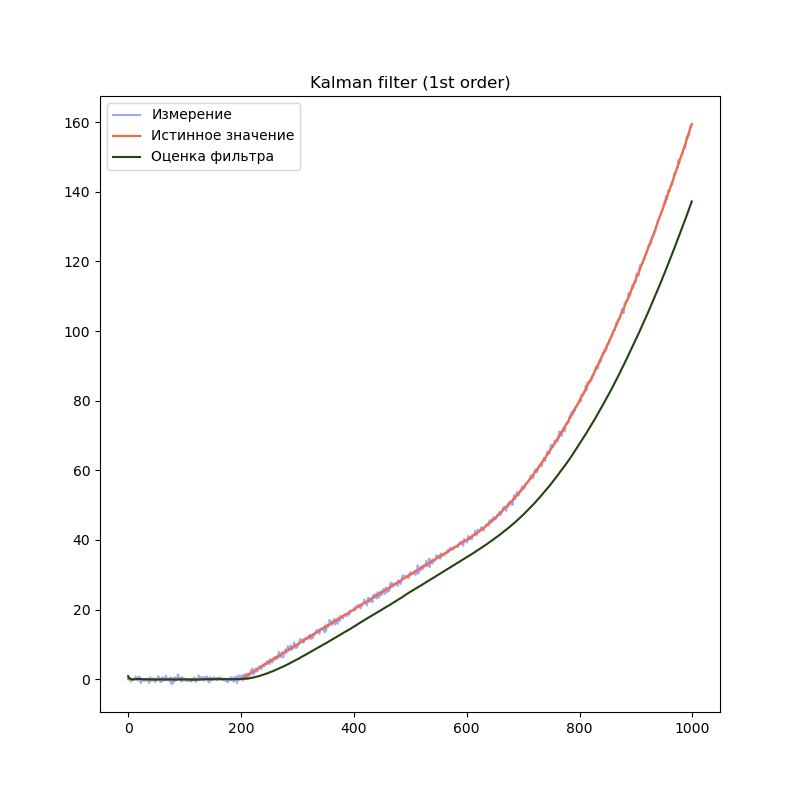

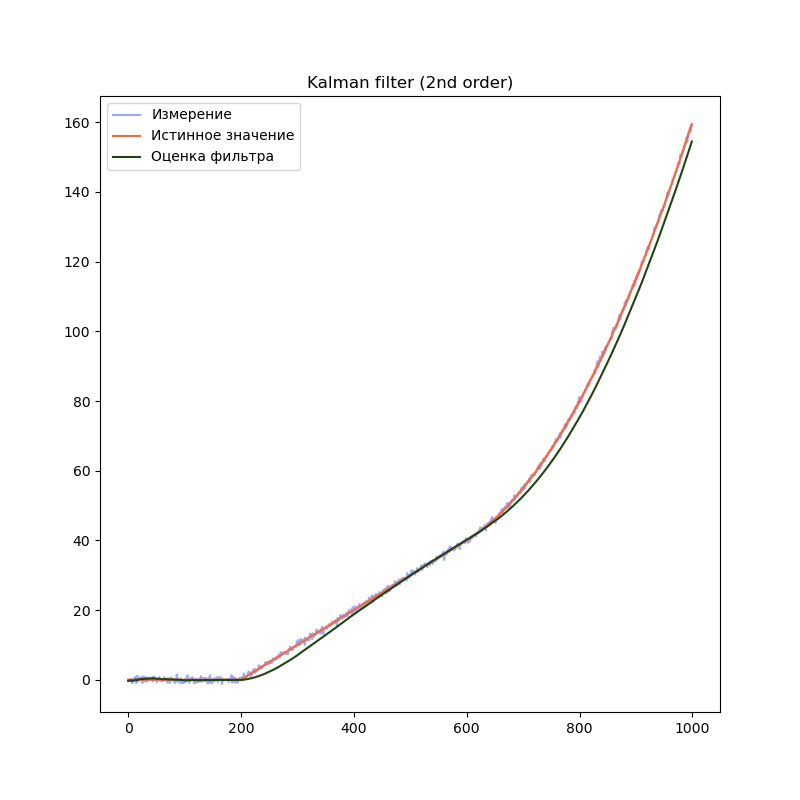
На графиках сразу заметно, что модель первого порядка начинает отставать от истинного значения на участках равномерного движения и равноускоренного движения. Модель второго порядка успешно справляется с участком равномерного движения, но так же начинает отставать на участке равноускоренного движения. Модель третьего порядка справляется со всеми тремя участками.

Однако, это не означает что нужно использовать модели высокого порядка во всех случаях. В нашем примере, модель третьего порядка справляется с участком равномерного движения несколько хуже модели второго порядка, т.к. фильтр интерпретирует шум сенсора как изменение ускорения. Это приводит к колебанию оценки фильтра. Стоит подбирать порядок модели в соответствии с планируемыми режимами работы фильтра.

Нелинейные модели и фильтр Калмана

Почему фильтр Калмана не работает для нелинейных моделей и что делать

Всё дело в нормальном распределении. При применении линейных преобразованийк нормально распределенной случайной величине, результирующее распределение будет представлять собой нормальное распределение, или будет пропорциональным нормальному распределению. Именно на этом принципе и строится математика фильтра Калмана.

Есть несколько модификаций алгоритма, которые позволяют работать с нелинейными моделями.

Extended Kalman Filter (EKF) — расширенный фильтр Калмана. Этот подход строит линейное приближение модели на каждом шаге. Для этого требуется рассчитать матрицу вторых частных производных функции модели, что бывает весьма непросто. В некоторых случаях, аналитическое решение найти сложно или невозможно, и поэтому используют численные методы.

Unscented Kalman Filter (UKF). Этот подход строит приближение распределения получающегося после нелинейного преобразования при помощи сигма-точек. Преимуществом этого метода является то, что он не требует вычисления производных.

Мы рассмотрим именно Unscented Kalman Filter

Unscented Kalman Filter и почему он без запаха

Основная магия этого алгоритма заключается в методе, который строит приближение распределения плотности вероятности случайной величины после прохождения через нелинейное преобразование. Этот метод называется unscented transform — сложнопереводимое на русский язык название. Автор этого метода, Джеффри Ульман, не хотел, чтобы его разработку называли “Фильтр Ульмана”. Согласно интервью, он решил назвать так свой метод после того как увидел дезодорант без запаха (“unscented deodorant”) на столе в лаборатории, где он работал.

Этот метод достаточно точно строит приближение функции распределения случайной величины, но что более важно — он очень простой.

Для использования UKF не придётся реализовывать какие-либо дополнительные вычисления, за исключением моделей системы. В общем виде, нелинейная модель не может быть представлена в виде матрицы, поэтому мы заменяем матрицы и на функции и . Однако смысл этих моделей остаётся тем же.

Реализуем unscented Kalman filter для линейной модели из прошлого примера:

Разница в коде минимальна. Мы заменили матрицы F и H на функции f(x) и h(x). Это позволяет использовать нелинейные модели системы и/или наблюдения:

Также, появилась строчка, устанавливающая алгоритм генерации сигма-точек

Этот алгоритм определяет точность оценки распределения вероятности при прохождении через нелинейное преобразование. К сожалению, существуют только общие рекомендации относительно генерации сигма-точек. Поэтому для каждой отдельной задачи значения параметров алгоритма подбираются экспериментальным путём.

Ожидаемый результат — график оценки положения практически не отличается от обычного фильтра Калмана.

Ожидаемый результат — график оценки положения практически не отличается от обычного фильтра Калмана.

В этом примере используется линейная модель. Однако мы могли бы использовать нелинейные функции. Например, мы могли бы использовать следующую реализацию:

Такую модель измерений было бы невозможно использовать в случае с линейным фильтром Калмана

Вместо заключения

За рамками статьи остались теоретические основы фильтра Калмана. Однако объем материала по этой теме ошеломляет. Сложно выбрать хороший источник. Я бы хотел рекомендовать замечательную книгу от автора библиотеки filterpy Roger Labbe (на английском языке). В ней доступно описаны принципы работы алгоритма и сопутствующая теория. Книга представляет собой документ Jupyter notebook, который позволяет в интерактивном режиме экспериментировать с примерами.

Источник